Содержание
- 2. Категории зависимости: 1) функциональные; 2) корреляционные. Функциональные связи характеризуются: полным соответствием между изменением факторного признака и
- 3. Задачи корреляционного анализа: выявлении взаимосвязи между случайными переменными путем точечной и интервальной оценки парных (частных) коэффициентов
- 4. Ковариация между двумя переменными Х и У рассчитывается следующим образом: где - фактические значения случайных переменных
- 5. Дисперсия (оценка дисперсии) характеризует степень разброса значений х1, х2, х3, …, хn (у1, у2, у3, …,
- 6. Среднеквадратическое отклонение или стандартное отклонение, или стандартная ошибка переменной Х (переменной Y) Оценка значимости коэффициента корреляции
- 7. Парная линейная регрессия Парная регрессия – это уравнение связи двух переменных и где независимая, объясняющая переменная
- 8. Пусть имеется набор значений двух переменных: Y= (у1, у2, у3, …, уn) - объясняемая переменная и
- 9. Таким образом, в уравнении (2) значение каждого наблюдения yi представлено как сумма двух частей — систематической
- 10. Свойства оценок МНК. Несмещенность оценки означает, что математическое ожидание остатков равно нулю. Оценки считаются эффективными, если
- 11. Такое решение может существовать только при выполнении условия что равносильно отличию от нуля определителя системы нормальных
- 12. = = = =
- 13. Оценка качества уравнения регрессии После построения уравнения регрессии мы можем разбить значение Y, в каждом наблюдении
- 14. Где - значения y, вычисленные по модели (4). Разделив правую и левую часть (4) на получим
- 15. Коэффициент детерминации Коэффициент детерминации показывает долю вариации результативного признака, находящегося под воздействием изучаемых факторов, т. е.
- 16. для оценки качества регрессионных моделей целесообразно использовать среднюю ошибку аппроксимации:
- 17. Для проверки значимости модели регрессии используется F-критерий Фишера, вычисляемый как отношение дисперсии исходного ряда и несмещенной
- 18. В качестве меры точности применяют несмещенную оценку дисперсии остаточной компоненты, которая представляет собой отношение суммы квадратов
- 19. Прогнозирование с применением уравнения регрессии Прогнозируемое значение переменной y получается при подстановке в уравнение регрессии ожидаемой
- 20. Нелинейные модели и их линеаризация Задача построения нелинейной модели регрессии состоит в следующем: Задана нелинейная спецификация
- 22. Скачать презентацию



















 Электрқондырғылардың істен шығуы
Электрқондырғылардың істен шығуы Блокада Ленинграда
Блокада Ленинграда Предварительное напряжение железобетона
Предварительное напряжение железобетона Проект Хлеб - всему голова
Проект Хлеб - всему голова Многопрофильная клиника ООО Медицинский центр жизнь
Многопрофильная клиника ООО Медицинский центр жизнь Презентация Сказка о жабе и розе Диск
Презентация Сказка о жабе и розе Диск Аварийно-спасательный инструмент. Вид и назначение аварийно-спасательного и механизированного инструмента
Аварийно-спасательный инструмент. Вид и назначение аварийно-спасательного и механизированного инструмента Объёмные таблицы стволов деревьев
Объёмные таблицы стволов деревьев Магнітний запис інформації
Магнітний запис інформації Краски осени
Краски осени Электроэнергетика России
Электроэнергетика России Цветы. Загадки о цветах
Цветы. Загадки о цветах Система управления парковочным пространством
Система управления парковочным пространством Фабрика карт. Изготовление пластиковых карт для сегмента B2B. Рекламный кейс
Фабрика карт. Изготовление пластиковых карт для сегмента B2B. Рекламный кейс Начертательная геометрия. Строительство
Начертательная геометрия. Строительство Конструирование одежды. 6 класс
Конструирование одежды. 6 класс Связь поляризованности диэлектрика в электростатическом поле с плотностью связанных зарядов
Связь поляризованности диэлектрика в электростатическом поле с плотностью связанных зарядов Презентация Знаки дорожного движения
Презентация Знаки дорожного движения История телевидения
История телевидения Из детства — в отрочество
Из детства — в отрочество Модели. Моделирование
Модели. Моделирование Первые полеты в космос. Белка и Стрелка
Первые полеты в космос. Белка и Стрелка Медицина Древнего Рима
Медицина Древнего Рима Сохранение здоровья и формирование потребности в здоровом образе жизни
Сохранение здоровья и формирование потребности в здоровом образе жизни Вторая мировая война (1939-1945)
Вторая мировая война (1939-1945) Совершенствование коррекционно-развивающей среды логопедического кабинета в условиях реализации ФГОС
Совершенствование коррекционно-развивающей среды логопедического кабинета в условиях реализации ФГОС Служебная дисциплина в органах внутренних дел Российской Федерации
Служебная дисциплина в органах внутренних дел Российской Федерации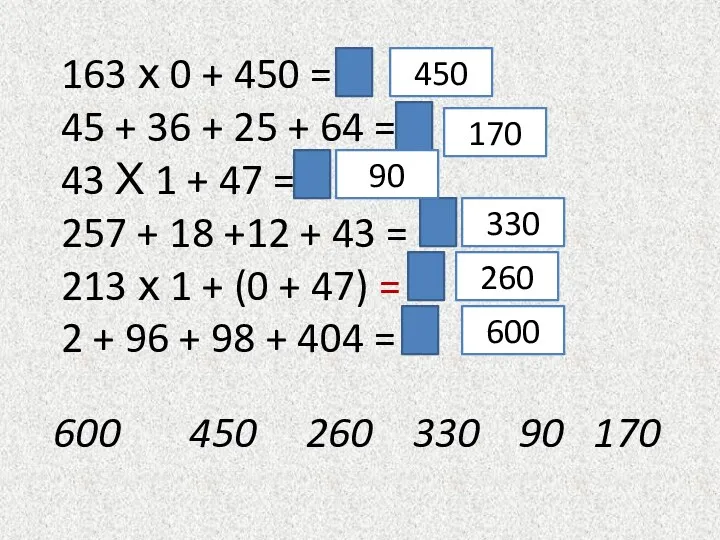 Презентация к уроку математики для 4 класса
Презентация к уроку математики для 4 класса