Доказательство:
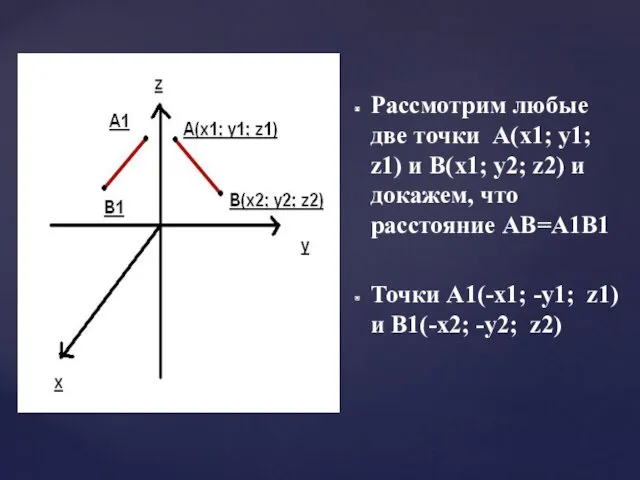
Пусть A и B — две произвольные точки фигуры F.
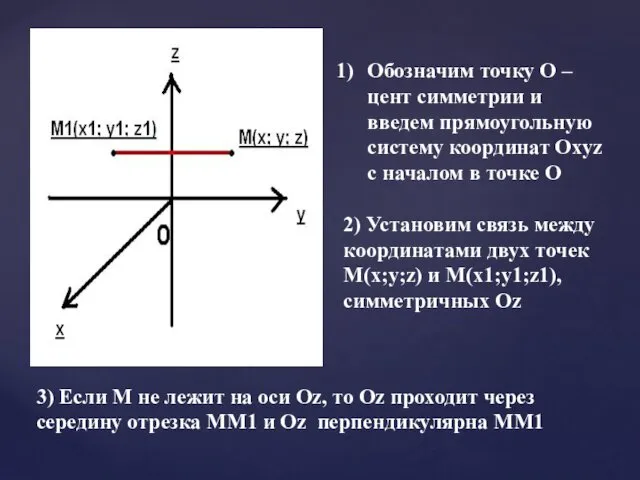
При симметрии
относительно точки O фигуры F точка A переходит в точку A1, точка B — в точку B1.
Рассмотрим треугольники AOB и A1OB.
1) AO=OA1
2) BO=OB1 (так как A и A1, B и B1 — точки, симметричные относительно точки O)
3) ∠AOB=∠B1OA1 (как вертикальные)
Следовательно, треугольники AOB и A1OB равны (по двум сторонам и углу между ними).
Из равенства треугольников следует равенство соответствующих сторон: AB=A1B1, то есть расстояние между точками сохраняется, а значит, преобразование симметрии относительно точки является движением.
Что и требовалось доказать.
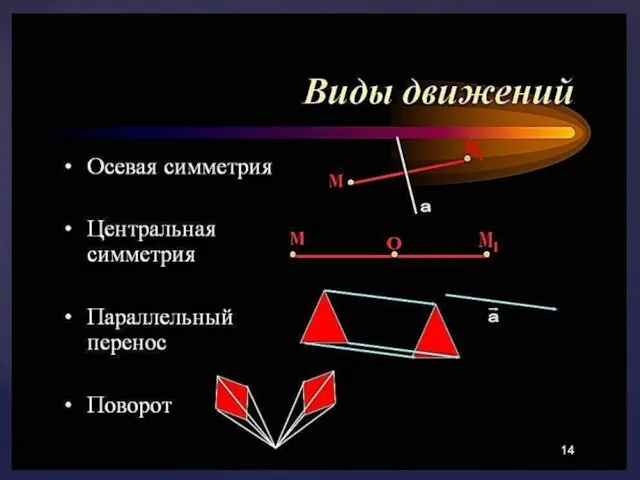
Теорема: Центральная симметрия
является движением








 Гражданская война в США (1861-1865). Империализм
Гражданская война в США (1861-1865). Империализм Николай Александрович Бердяев
Николай Александрович Бердяев Презентация № 3 Воздух, которым мы дышим
Презентация № 3 Воздух, которым мы дышим Діагностування пристроїв заземлення
Діагностування пристроїв заземлення Критерии оценивания курсовой и выпускной квалификационной работы
Критерии оценивания курсовой и выпускной квалификационной работы Деятельность руководителя по управлению деловой карьерой персонала
Деятельность руководителя по управлению деловой карьерой персонала Исследование и оценка физического развития. Функциональные пробы
Исследование и оценка физического развития. Функциональные пробы Государственная поддержка малого предпринимательства. ООО СтройЭкспертСтрелка
Государственная поддержка малого предпринимательства. ООО СтройЭкспертСтрелка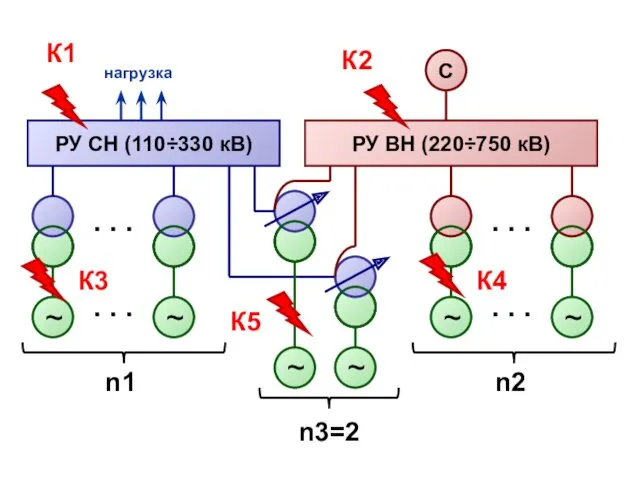 Расчёт ТКЗ схемы замещения
Расчёт ТКЗ схемы замещения Презентация 1
Презентация 1 Проект складной рыбацкий стулик
Проект складной рыбацкий стулик Сальмонеллалар, микробиологиялық диагностика, алдын-алу мен емдеу жолдары
Сальмонеллалар, микробиологиялық диагностика, алдын-алу мен емдеу жолдары Презентация Климат и климатические ресурсы
Презентация Климат и климатические ресурсы Эволюционная теория Дарвина
Эволюционная теория Дарвина Монастыри, основанные учениками преподобного Сергия Радонежского
Монастыри, основанные учениками преподобного Сергия Радонежского Государственный историко-архитектурный и этнографический музей-заповедник Кижи
Государственный историко-архитектурный и этнографический музей-заповедник Кижи Оборудование по теме Порошки
Оборудование по теме Порошки Совершенствование законодательства в области гражданской обороны и защиты населения и территорий от чрезвычайных ситуаций
Совершенствование законодательства в области гражданской обороны и защиты населения и территорий от чрезвычайных ситуаций Презентация к открытому мероприятию для учащихся 1 класса по правилам дорожного движения. Путешествие в страну дорожных знаков.
Презентация к открытому мероприятию для учащихся 1 класса по правилам дорожного движения. Путешествие в страну дорожных знаков. Комплектация и коммутация щитов
Комплектация и коммутация щитов Проектная работа
Проектная работа Наша Фаня
Наша Фаня Жизнь первых людей на Земле
Жизнь первых людей на Земле Биологическая роль отдельных микро-и ультрамикроэлементов в организме животных
Биологическая роль отдельных микро-и ультрамикроэлементов в организме животных Экономико-математическое моделирование
Экономико-математическое моделирование Основы проектирования машин. Редукторы со сборочным узлом
Основы проектирования машин. Редукторы со сборочным узлом Победа или поражение. Сочинение по пьесе А.Н.Островского Гроза
Победа или поражение. Сочинение по пьесе А.Н.Островского Гроза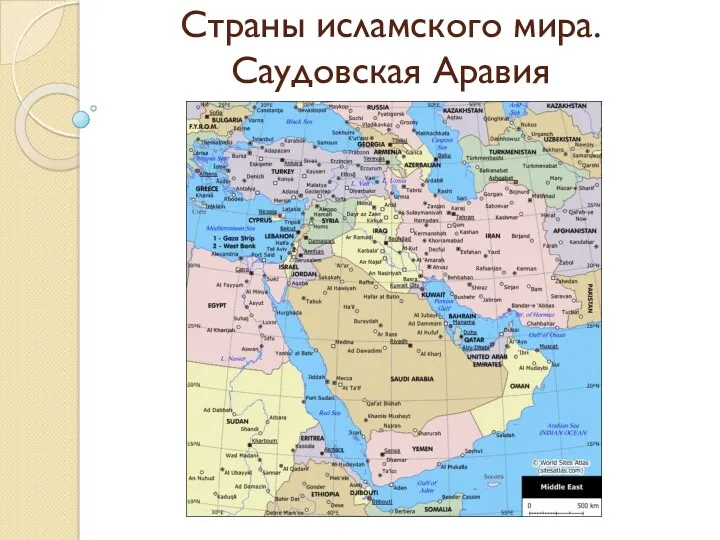 Страны исламского мира. Саудовская Аравия
Страны исламского мира. Саудовская Аравия