Содержание
- 2. Содержание Приращение функции Геометрический смысл приращения функции Понятие производной. Алгоритм нахождения производнойАлгоритм нахождения производной. Примеры. Таблица
- 3. Приращение функции
- 4. 4 3 2 1 у х 2 -2 -1 1 0 Дан график функции у=4-х2 По
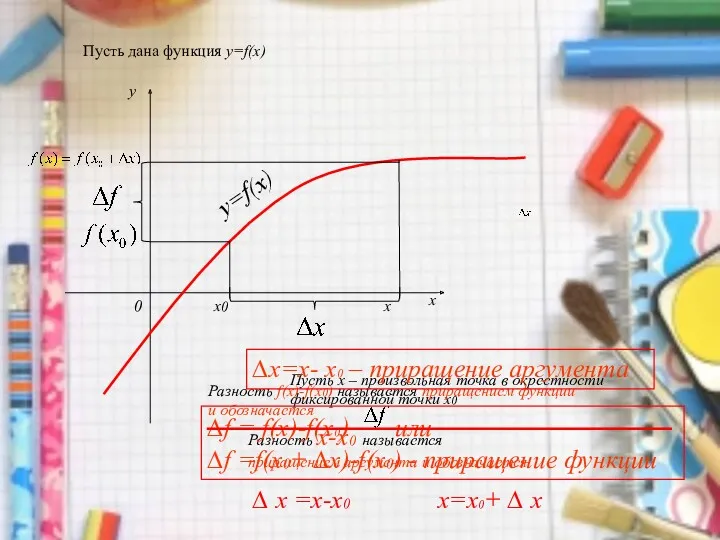
- 5. у=f(х) Пусть дана функция у=f(х) y x 0 х х0 Пусть х – произвольная точка в
- 6. Пример 1: Найти приращение аргумента и приращение функции в точке х0, если Решение: Содержание
- 7. Геометрический смысл приращения функции у=f(х) y x 0 х х0 Прямая l , проходящая через любые
- 8. Содержание Пример
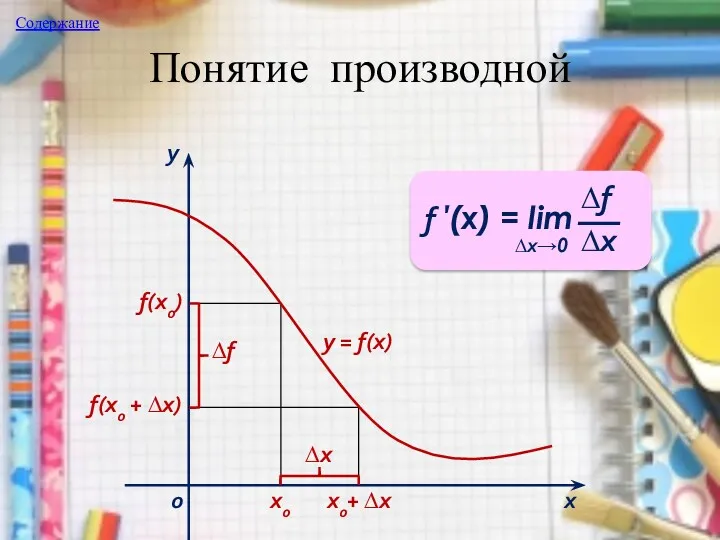
- 9. Понятие производной Производной функции у = f(x), заданной на некотором интервале (a; b), в некоторой точке
- 10. Понятие производной х0 х0+ ∆х f(x0) f(x0 + ∆х) ∆х х у 0 ∆f у =
- 11. Зафиксировать значение х0, найти f(x0). Дать аргументу х0 приращение ∆х, перейти в новую точку х0 +
- 12. Примеры 1. Найти производную функции y = kx + b в точке хo Содержание
- 13. Примеры 2. Найти производную функции y = C (C – const) в точке хo Содержание
- 14. Примеры 3. Найти производную функции y = x2 в точке хo Содержание
- 15. Примеры Содержание
- 16. Примеры Содержание
- 17. Примеры 5. Найти производную функции y = 1/x в точке хo Содержание
- 18. Примеры 5. Найти производную функции y = 1/x в точке хo Содержание
- 20. Скачать презентацию


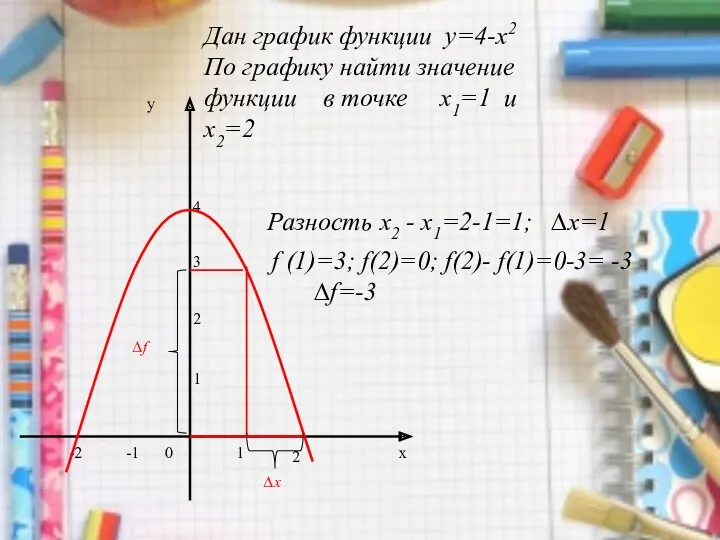












 Как хороша ты, родная весна!
Как хороша ты, родная весна! Водный транспорт. Морской и речной транспорт
Водный транспорт. Морской и речной транспорт Этапы вязания крючком
Этапы вязания крючком Компанія ЗМ
Компанія ЗМ Принципы имитационного моделирования. Математические методы моделирования
Принципы имитационного моделирования. Математические методы моделирования Словарные слова (1-2 класс)
Словарные слова (1-2 класс) Визволення України від нацистських загарбників
Визволення України від нацистських загарбників Компанія Federal. Розподільче обладнання
Компанія Federal. Розподільче обладнання Halloween. On the 31st of October British people celebrate Halloween
Halloween. On the 31st of October British people celebrate Halloween Единые сроки каникул в московских школах
Единые сроки каникул в московских школах Глобальные сети и перспективные сетевые технологии. Глобальные сети (Wide Area Networks, WAN)
Глобальные сети и перспективные сетевые технологии. Глобальные сети (Wide Area Networks, WAN) презентация 6 класс Горные породы и минералы
презентация 6 класс Горные породы и минералы Федеральные СМИ
Федеральные СМИ Leongardt_mikrofinansovye_organizatsii
Leongardt_mikrofinansovye_organizatsii Брюгге. Достопримечательности
Брюгге. Достопримечательности Бронхиальная астма
Бронхиальная астма Формирование у детей старшего дошкольного возраста положительной учебной мотивации
Формирование у детей старшего дошкольного возраста положительной учебной мотивации Проверочная работа по теме Мировой океан Диск
Проверочная работа по теме Мировой океан Диск История и методология науки
История и методология науки Презентация Металлические деньги в истории России
Презентация Металлические деньги в истории России Программная обработка данных на компьютере
Программная обработка данных на компьютере Праздник Троицы. Церковное песнопение,
Праздник Троицы. Церковное песнопение, Счетчики. Четырехразрядный суммирующий асинхронный двоичный счетчик
Счетчики. Четырехразрядный суммирующий асинхронный двоичный счетчик Электронный конструктор Знаток
Электронный конструктор Знаток Интегрированный урок по английскому языку и физической культуре. 3 класс
Интегрированный урок по английскому языку и физической культуре. 3 класс Энергетические характеристики агрегатов и ГЭС
Энергетические характеристики агрегатов и ГЭС Защита прав человека в Японии
Защита прав человека в Японии Лепка фигуры человека с каркасом
Лепка фигуры человека с каркасом