Содержание
- 2. Общий план курса Случайные процессы и методы их описания. Модели случайных процессов. Шумовые колебания в линейных
- 3. Модели случайных процессов (план) см [1]. Глава 2 Спектральный анализ сигналов Гауссовский случайный процесс Узкополосный стационарный
- 4. Спектральный анализ сигналов Периодические сигналы Где ω - круговая частота, n - любое положительное целое число
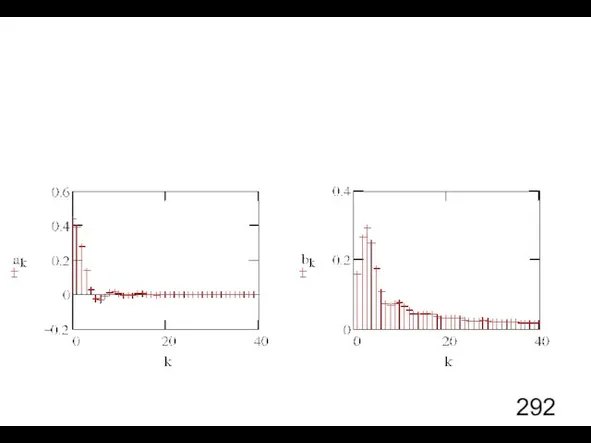
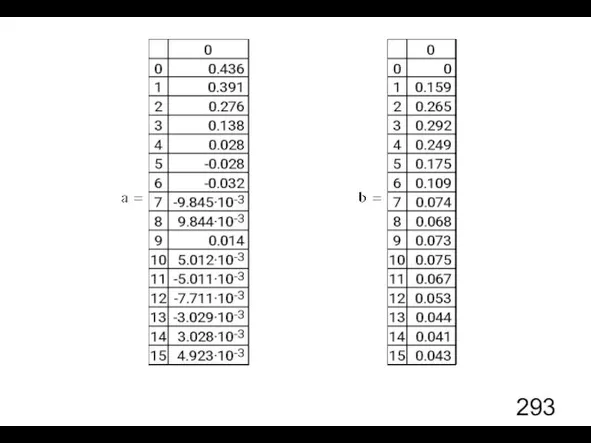
- 5. Коэффициенты разложения ряда Фурье
- 6. Формы представления ряда Фурье
- 7. Формы представления ряда Фурье
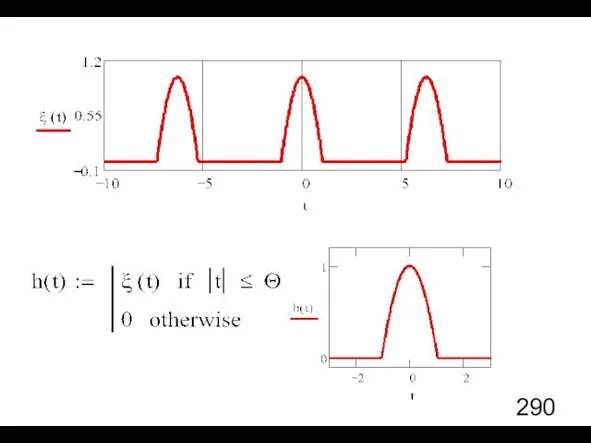
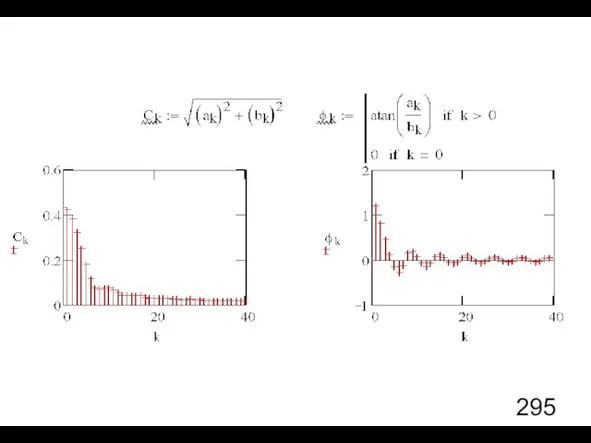
- 8. Пример 1. Периодическая последовательность косинусоидальных импульсов.
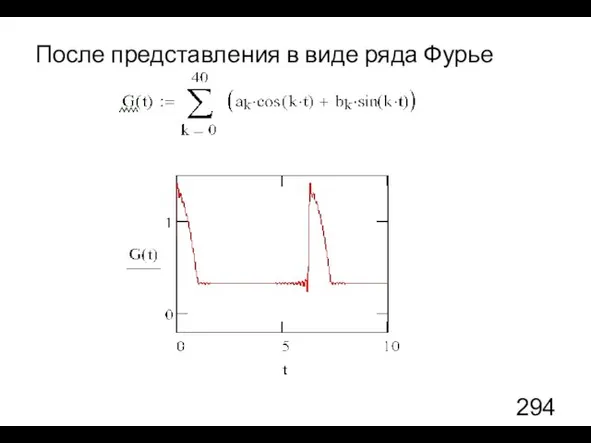
- 13. После представления в виде ряда Фурье
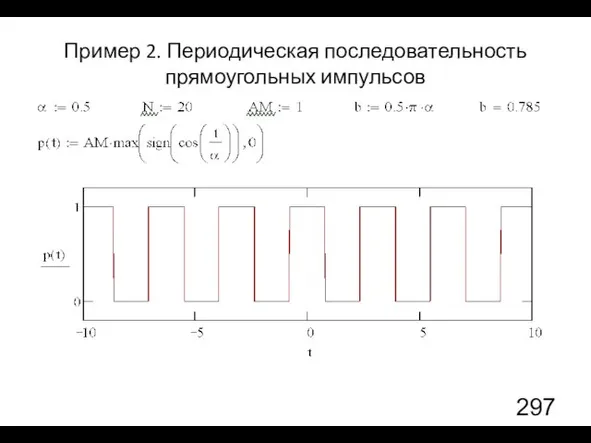
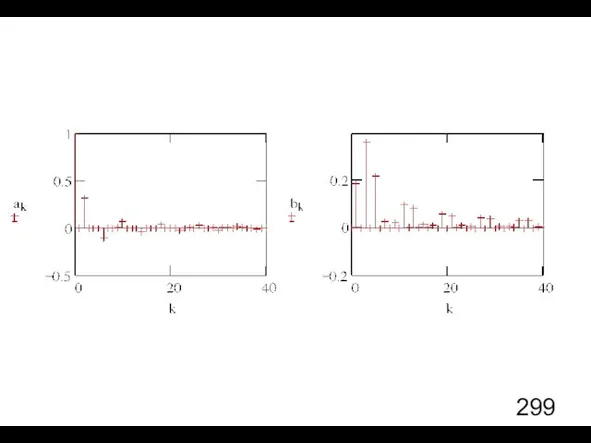
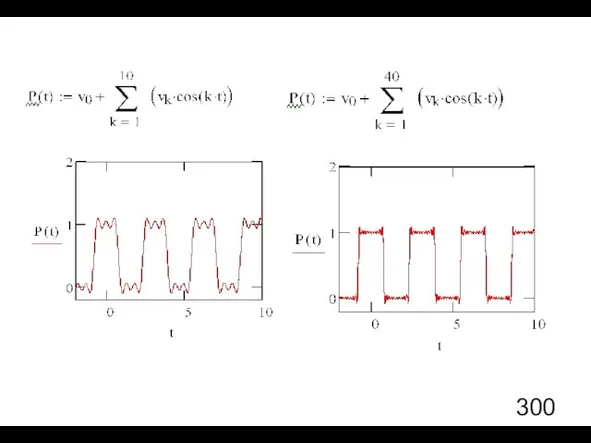
- 16. Пример 2. Периодическая последовательность прямоугольных импульсов
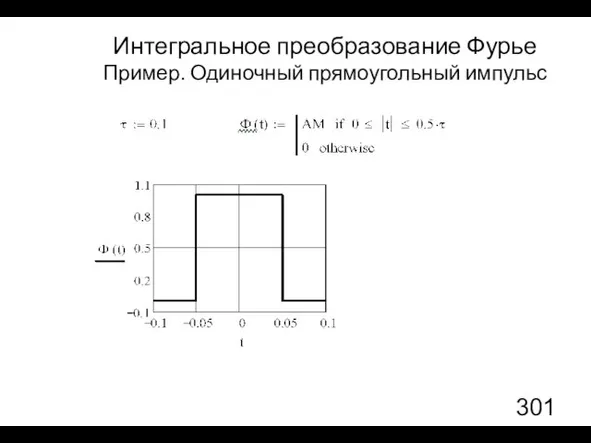
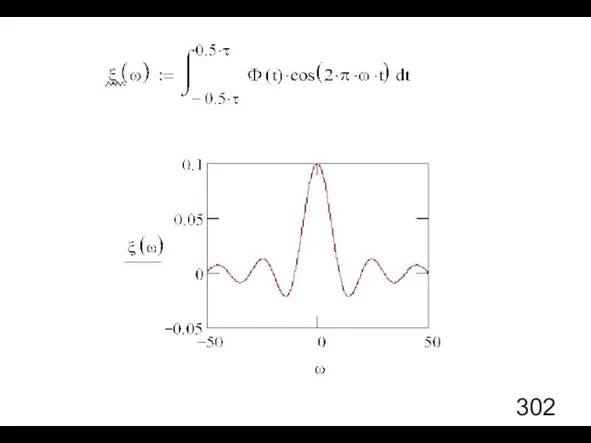
- 20. Интегральное преобразование Фурье Пример. Одиночный прямоугольный импульс
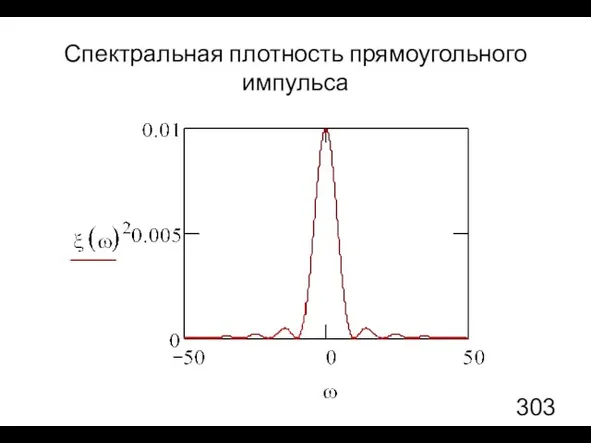
- 22. Спектральная плотность прямоугольного импульса
- 23. Модели случайных процессов (план) см [1]. Глава 2 Спектральный анализ сигналов Гауссовский случайный процесс Узкополосный стационарный
- 24. Гауссовский случайный процесс Многомерная гауссовская плотность вероятности Смысл параметров гауссовской плотности вероятности:
- 25. Гауссовский случайный процесс-2 Одномерная плотность вероятности
- 26. Гауссовский случайный процесс-3 Одномерная плотность вероятности примет вид: В этой формуле все параметры выражены через экспериментально
- 27. Гауссовский случайный процесс-4 Свойства одномерного распределения. Отличны от нуля лишь четные центральные моменты
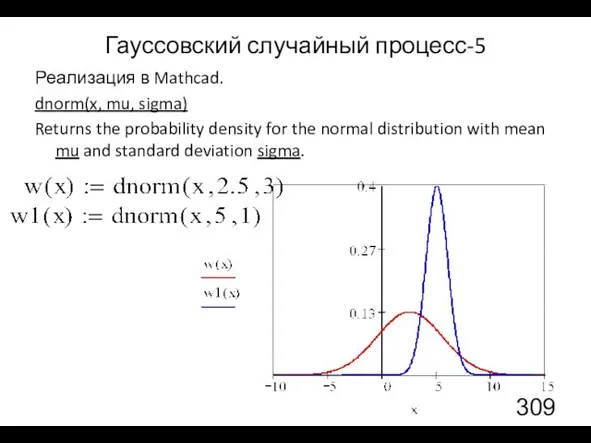
- 28. Гауссовский случайный процесс-5 Реализация в Mathcad. dnorm(x, mu, sigma) Returns the probability density for the normal
- 29. Гауссовский случайный процесс-6 Применение для случайных процессов
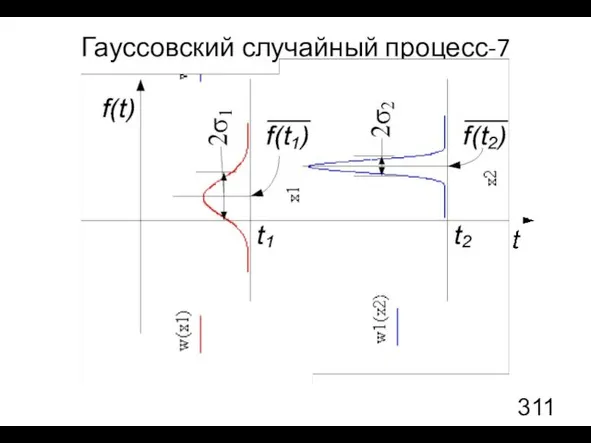
- 30. Гауссовский случайный процесс-7
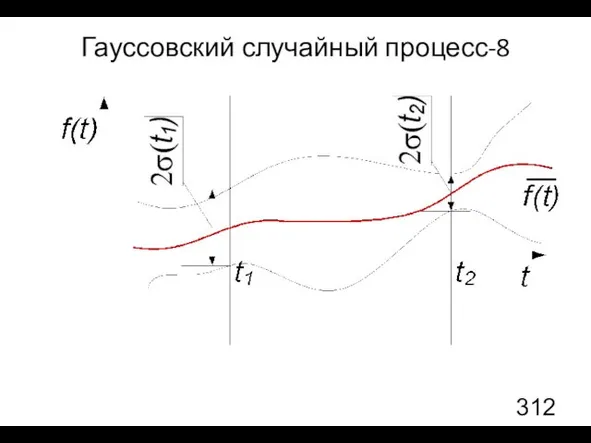
- 31. Гауссовский случайный процесс-8
- 32. Гауссовский случайный процесс-9 Для вычисления корреляционного момента достаточно парной (для 2-х переменных) плотности вероятности Наша цель
- 33. Гауссовский процесс-10
- 34. Гауссовский процесс-11 Таким образом, плотность вероятности может быть выражена через экспериментально измеримые величины: Рассмотрим применение распределения
- 35. Гауссовский процесс-12
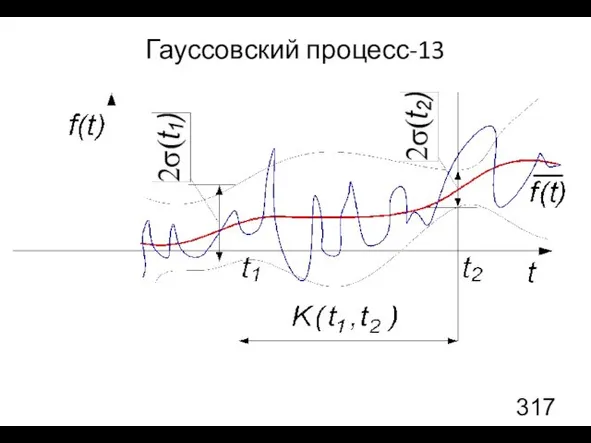
- 36. Гауссовский процесс-13
- 37. Гауссовский случайный процесс-14 Выводы: 1. Если процесс гауссовский, то все его характеристики можно вычислить. Любые моменты
- 38. Модели случайных процессов (план) см [1]. Глава 2 Спектральный анализ сигналов Гауссовский случайный процесс Узкополосный стационарный
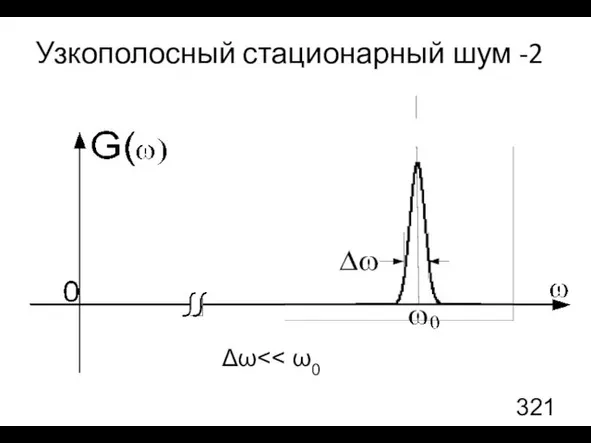
- 39. Узкополосный стационарный шум Шум узкополосный, если спектральная плотность G(ω) отлична от нуля в узкой области частот
- 40. Узкополосный стационарный шум -2 Δω
- 41. Узкополосный стационарный шум -2 Флуктуационную компоненту представим в виде (модель узкополосного шума): где ρ(t) – огибающая
- 42. Вместо огибающей и фазы также вводят квадратурные компоненты a(t), b(t) Таким образом, мы выделяем функции времени
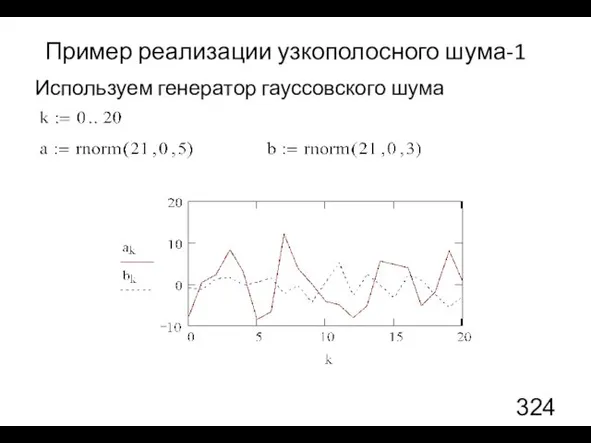
- 43. Пример реализации узкополосного шума-1 Используем генератор гауссовского шума
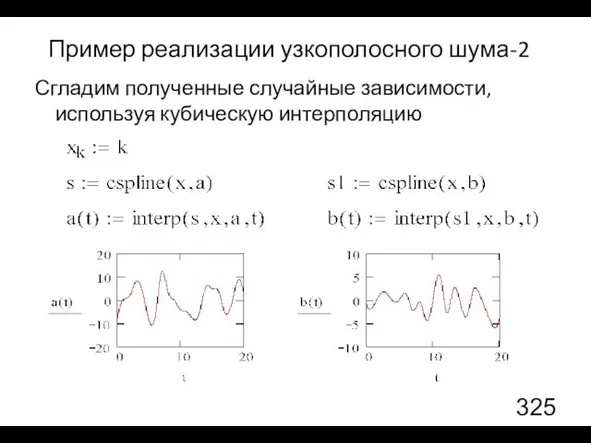
- 44. Пример реализации узкополосного шума-2 Сгладим полученные случайные зависимости, используя кубическую интерполяцию
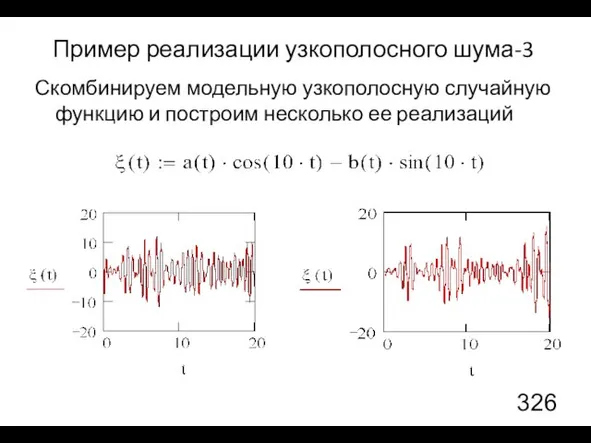
- 45. Пример реализации узкополосного шума-3 Скомбинируем модельную узкополосную случайную функцию и построим несколько ее реализаций
- 46. Постановка задачи: Задача: зная свойства шума ξ(t) найти статистические характеристики огибающей и фазы или квадратурных компонент.
- 47. Корреляционные и спектральные характеристики квадратурных компонент Предполагаем, что . Так как то Переходим к анализу корреляционной
- 48. Считаем известной корреляционную функцию Подставим в эту формулу представление через квадратурные компоненты
- 49. Учтем известные тригонометрические формулы Подставим эти выражения в приведенное выше выражение
- 50. В силу стационарности здесь не должно быть явной зависимости от времени, поэтому Это следует из равноправности
- 51. Где введена безразмерная корреляционная функция
- 52. Чтобы найти неизвестные функции воспользуемся формулой Винера-Хинчина: Интеграл от нечетной функции (содержит sin(ωτ)) равен нулю. В
- 55. При этом предположении Имеет свойства корреляционной функции
- 56. Модели случайных процессов (план) см [1]. Глава 2 Спектральный анализ сигналов Гауссовский случайный процесс Узкополосный стационарный
- 57. Узкополосный стационарный гауссовский шум
- 58. Найдем плотность вероятности переменных и
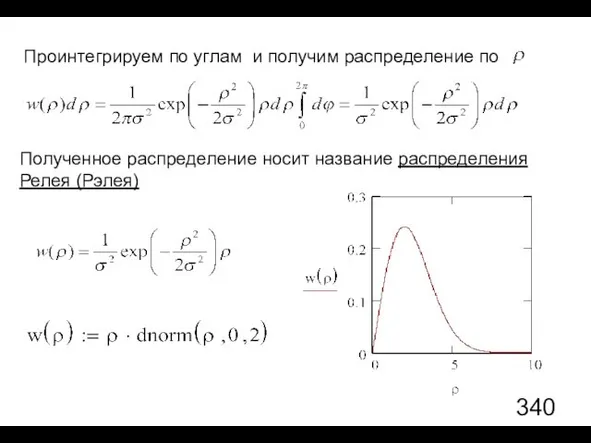
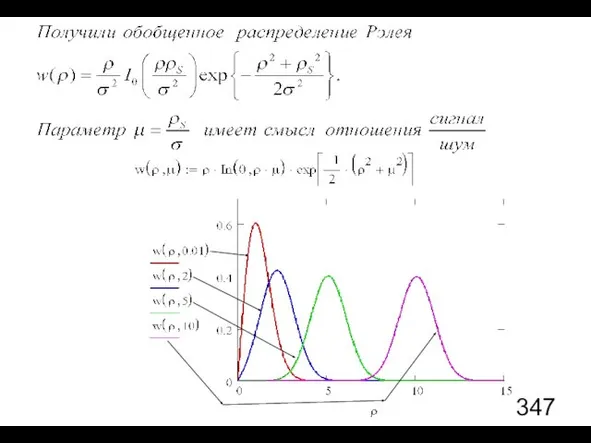
- 59. Проинтегрируем по углам и получим распределение по Полученное распределение носит название распределения Релея (Рэлея)
- 60. Моменты распределения Рэлея:
- 61. Используем полученные результаты для анализа суперпозиции гармонического сигнала и гауссовского шума. Случайный процесс имеет вид «Сигнал»
- 62. Будем искать вероятностные характеристики огибающей и фазы, и процесса х(t). Исходим из распределения квадратурных компонент шума:
- 63. Будем искать распределение по ρ
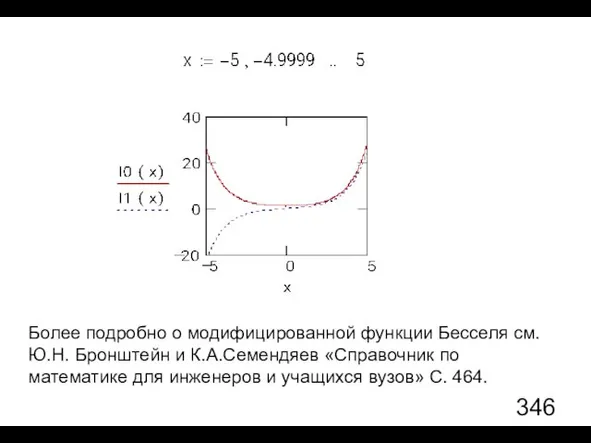
- 65. Более подробно о модифицированной функции Бесселя см. Ю.Н. Бронштейн и К.А.Семендяев «Справочник по математике для инженеров
- 67. Замечание об использовании Mathcad. В Mathcad имеется специальная функция Returns the m-th order modified Bessel function
- 68. Обсуждение результатов В пределе сильного шума, когда μ
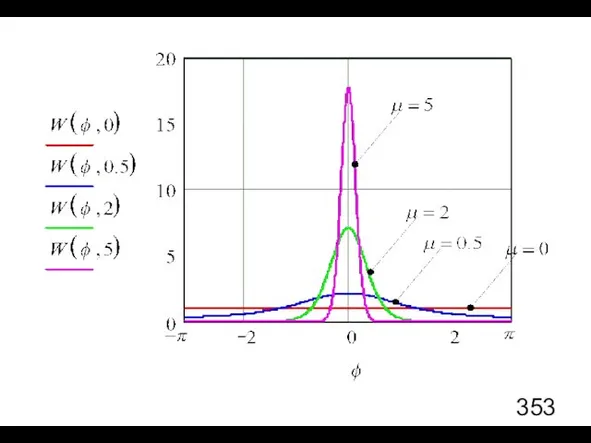
- 69. Распределение фазы
- 70. В предельных случаях
- 71. Построение графика W(φ,μ) средствами Mathcad где использована специальная функция (Function Category - Special) erf(z) Returns the
- 73. Модели случайных процессов (план) см [1]. Глава 2 Спектральный анализ сигналов Гауссовский случайный процесс Узкополосный стационарный
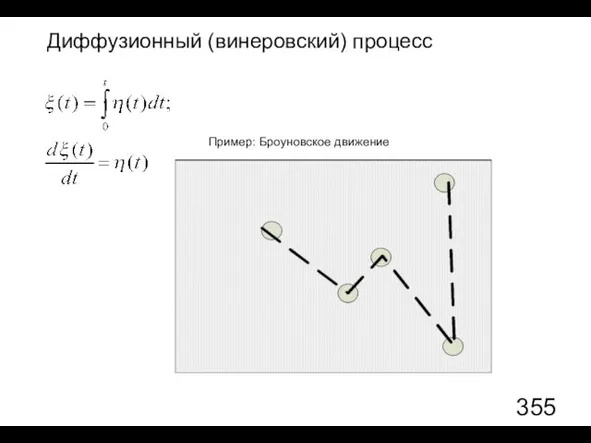
- 74. Диффузионный (винеровский) процесс Пример: Броуновское движение
- 75. переопределение времени
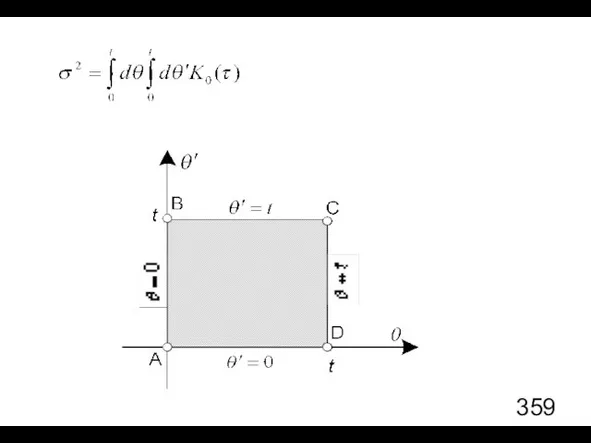
- 76. Постановка задачи: найти вероятностные свойства процесса ξ(t), зная свойства процесса η(t). Пусть известно, что: Требуется найти:
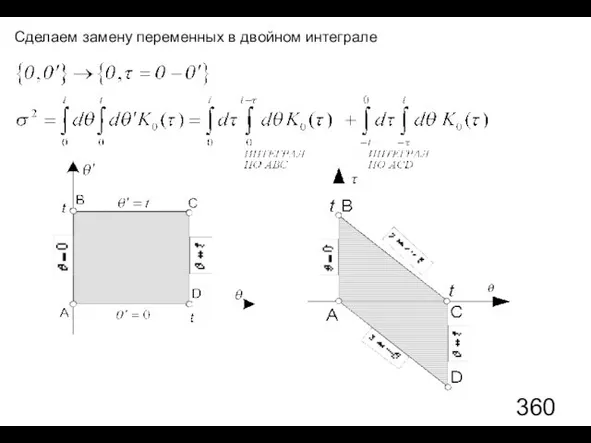
- 79. Сделаем замену переменных в двойном интеграле
- 83. t = 2 t = 1
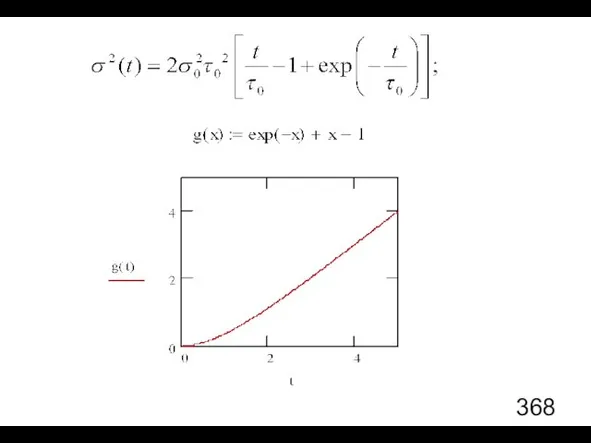
- 84. Вывод: Даже если шум «на входе» η(t) стационарный, винеровский процесс ξ(t) «на выходе» нестационарный:
- 85. Предельный случай t → 0
- 86. Конечное время корреляции Символьное вычисление интеграла с помощью MathCad:
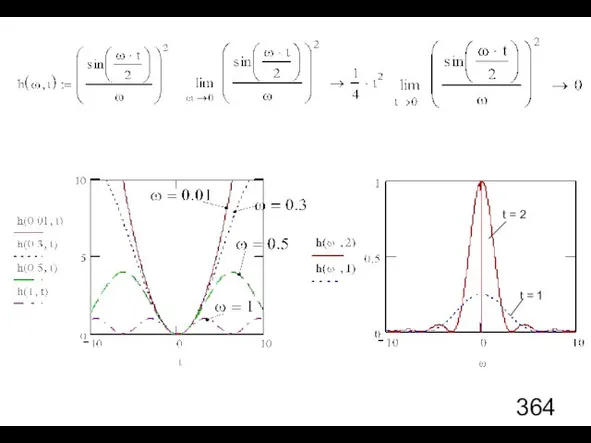
- 88. Предельный случай t → ∞
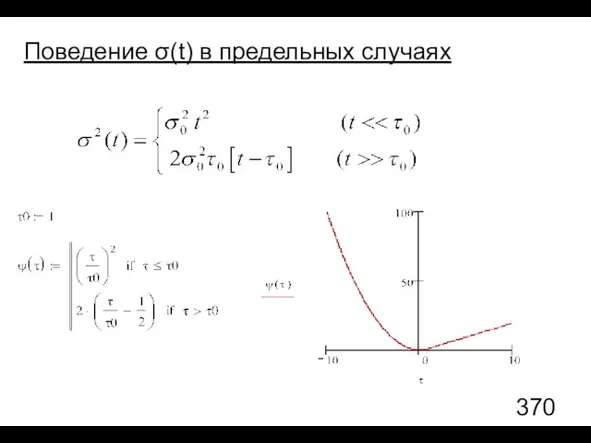
- 89. Поведение σ(t) в предельных случаях
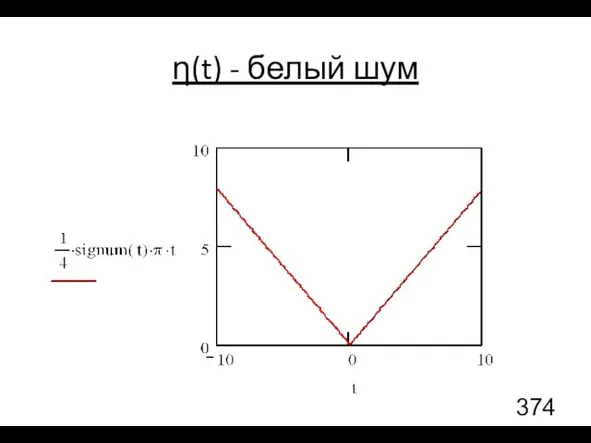
- 90. η(t) - белый шум
- 91. η(t) - белый шум
- 92. η(t) - белый шум
- 93. η(t) - белый шум
- 94. η(t) - белый шум
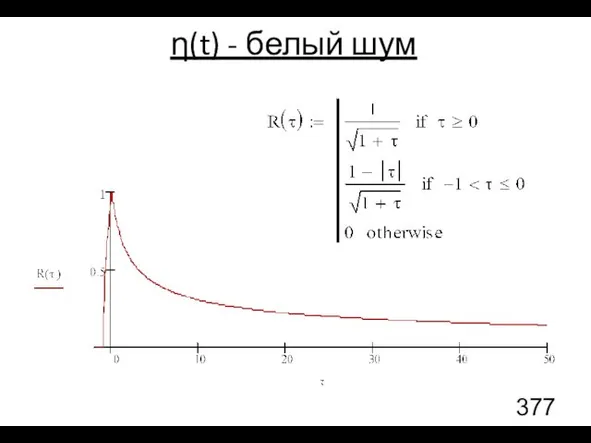
- 95. η(t) - белый шум Для этого частного случая можно также вычислить корреляционную функцию (без вывода) и
- 96. η(t) - белый шум
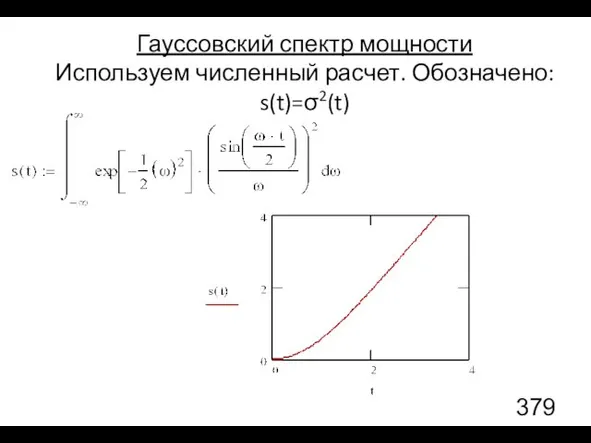
- 97. Гауссовский спектр мощности Используем формулу
- 98. Гауссовский спектр мощности Используем численный расчет. Обозначено: s(t)=σ2(t)
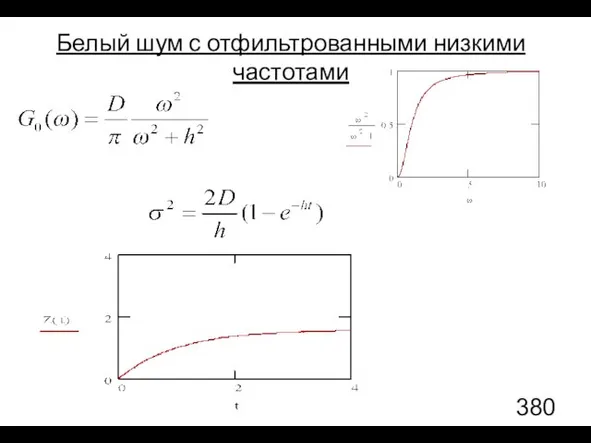
- 99. Белый шум с отфильтрованными низкими частотами
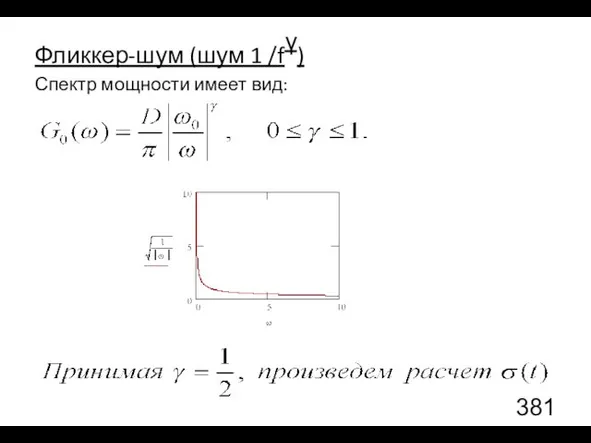
- 100. Фликкер-шум (шум 1 /fγ) Спектр мощности имеет вид:
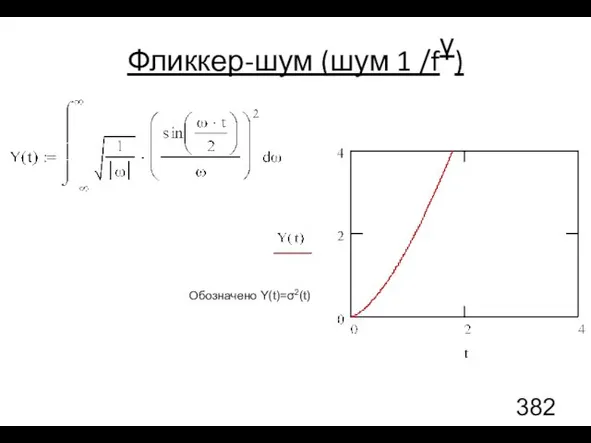
- 101. Фликкер-шум (шум 1 /fγ) Обозначено Y(t)=σ2(t)
- 102. Фликкер-шум (шум 1 /fγ)
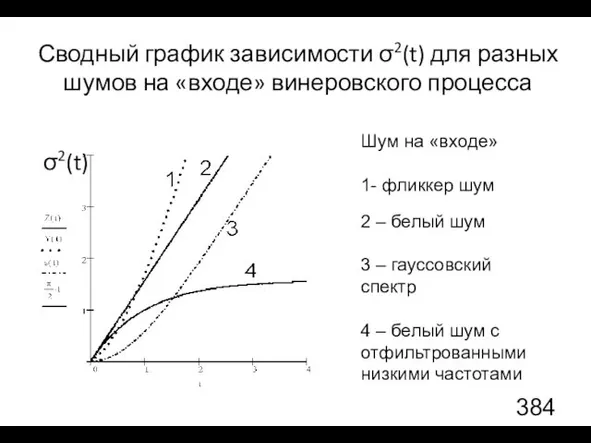
- 103. Сводный график зависимости σ2(t) для разных шумов на «входе» винеровского процесса Шум на «входе» 1- фликкер
- 104. Модели случайных процессов (план) см [1]. Глава 2 Спектральный анализ сигналов Гауссовский случайный процесс Узкополосный стационарный
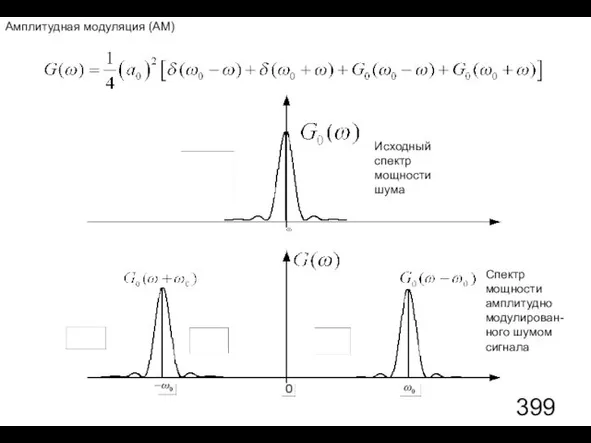
- 105. Колебания, модулированные шумом. Амплитудная модуляция (АМ) шумом Amplitude - амплитуда Постановка задачи: Задан шум Постановка задачи
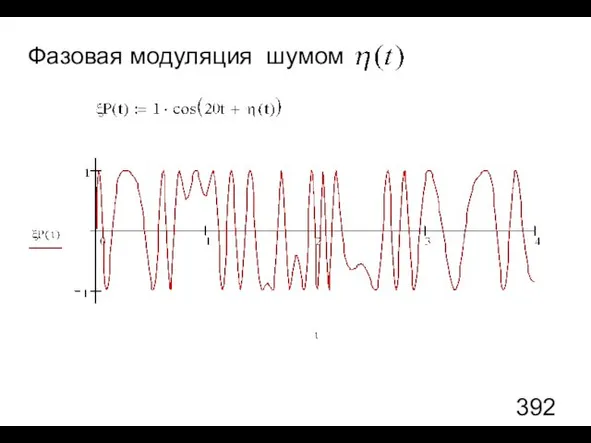
- 106. Колебания, модулированные шумом. Фазовая модуляция (ФМ) шумом Phase – фаза Постановка задачи: Задан шум Постановка задачи
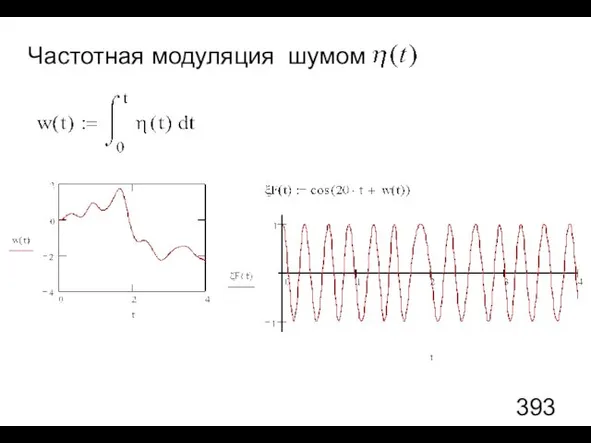
- 107. Колебания, модулированные шумом. Частотная модуляция (ЧМ) шумом Frequency - частота Постановка задачи: Задан шум Постановка задачи
- 108. Подготовка шума
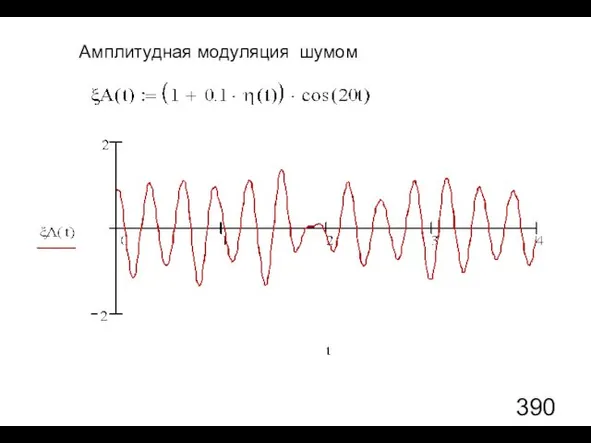
- 109. Амплитудная модуляция шумом
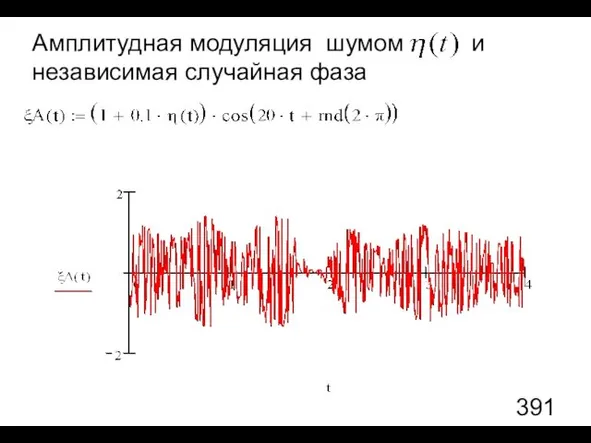
- 110. Амплитудная модуляция шумом и независимая случайная фаза
- 111. Фазовая модуляция шумом
- 112. Частотная модуляция шумом
- 113. Найдем среднее от ξ Амплитудная модуляция (АМ) подробно
- 114. Ищем корреляционную функцию процесса ξ Амплитудная модуляция (АМ) Здесь подразумевается усреднение по случайной фазе 0:
- 115. Амплитудная модуляция (АМ)
- 116. Перейдем к вычислению спектральной плотности процесса ξ(t) Амплитудная модуляция (АМ) (1) (2) (1)
- 117. Амплитудная модуляция (АМ) (2)
- 118. Исходный спектр мощности шума Спектр мощности амплитудно модулирован- ного шумом сигнала Амплитудная модуляция (АМ)
- 119. Колебания, модулированные шумом Фазовая модуляция (ФМ) гауссовским шумом Предположим, что - стационарный гауссовский процесс.
- 120. Фазовая модуляция (ФМ) гауссовским шумом Задача состоит в том, чтобы найти статистические характеристики сигнала x(t)
- 121. Для усреднения функции двух переменных ϕ(t) и ϕ(t+τ) также используем распределение Гаусса (для двух переменных). Фазовая
- 122. Введем флуктуационную компоненту фазово-модулированного сигнала: Таким образом, фазово-модулированный сигнал оказывается нестационарным случайным процессом. Фазовая модуляция (ФМ)
- 123. Зависимость от времени периодическая. Проведем также усреднение всех величин по периоду колебаний (по времени), так как
- 124. Фазовая модуляция (ФМ)
- 125. Мы видим, что спектр состоит из непрерывной компоненты и двух дискретных Дискретные компоненты Непрерывная компонента Введем
- 127. При слабой модуляции сигнала:
- 128. Колебания, модулированные шумом Частотная модуляция (ЧМ)-1 Т.о., фаза Ф(t) является диффузионным (винеровским) случайным процессом Здесь η(t)
- 129. Частотная модуляция (ЧМ)-2 Зададим свойства шума η(t): 1) шум считаем стационарным; 2) Наша задача: исследовать статистические
- 130. Частотная модуляция (ЧМ)-3 Как мы знаем из свойств диффузионного процесса (см. выше, формула ⊗) при любой
- 131. Частотная модуляция (ЧМ)-4 В дальнейшем считаем шум η(t) гауссовским. Используя полученные выше результаты для фазовой модуляции
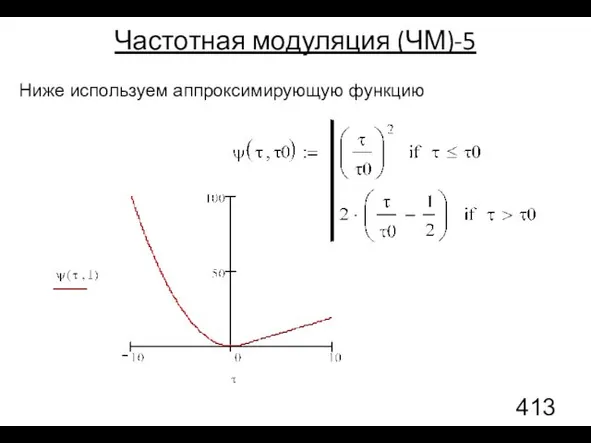
- 132. Частотная модуляция (ЧМ)-5 Ниже используем аппроксимирующую функцию
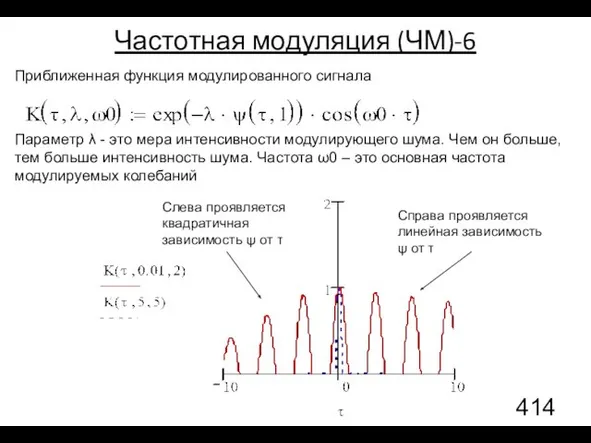
- 133. Частотная модуляция (ЧМ)-6 Приближенная функция модулированного сигнала Слева проявляется квадратичная зависимость ψ от τ Справа проявляется
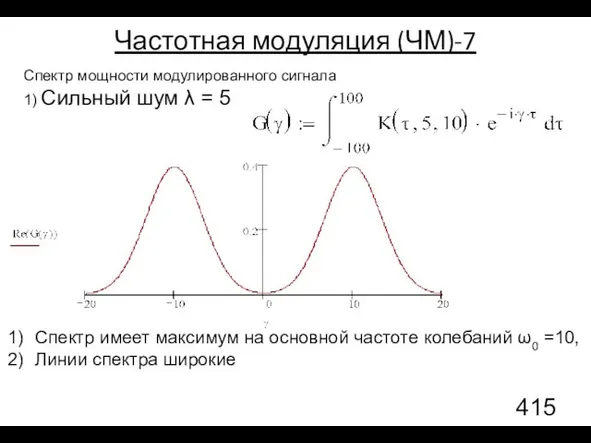
- 134. Частотная модуляция (ЧМ)-7 Спектр мощности модулированного сигнала 1) Сильный шум λ = 5 Спектр имеет максимум
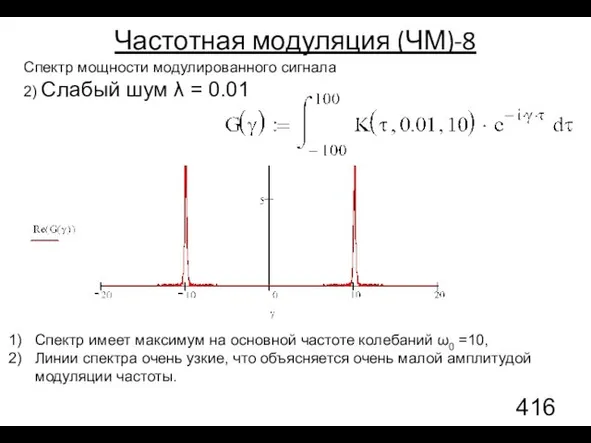
- 135. Спектр мощности модулированного сигнала 2) Слабый шум λ = 0.01 Частотная модуляция (ЧМ)-8 Спектр имеет максимум
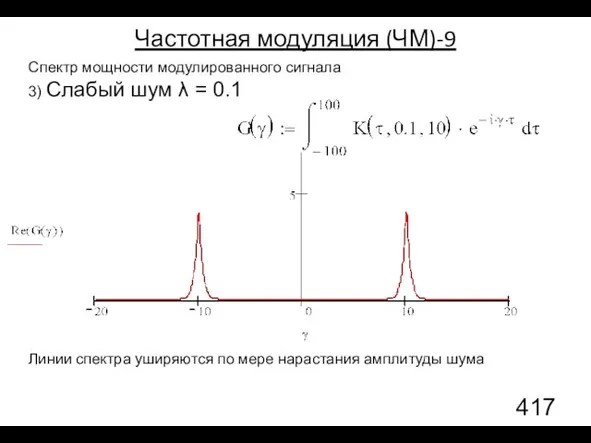
- 136. Спектр мощности модулированного сигнала 3) Слабый шум λ = 0.1 Частотная модуляция (ЧМ)-9 Линии спектра уширяются
- 138. Скачать презентацию

![Модели случайных процессов (план) см [1]. Глава 2 Спектральный анализ](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/36579/slide-2.jpg)








![Модели случайных процессов (план) см [1]. Глава 2 Спектральный анализ](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/36579/slide-22.jpg)










![Модели случайных процессов (план) см [1]. Глава 2 Спектральный анализ](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/36579/slide-37.jpg)













![Модели случайных процессов (план) см [1]. Глава 2 Спектральный анализ](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/36579/slide-55.jpg)












![Модели случайных процессов (план) см [1]. Глава 2 Спектральный анализ](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/36579/slide-72.jpg)




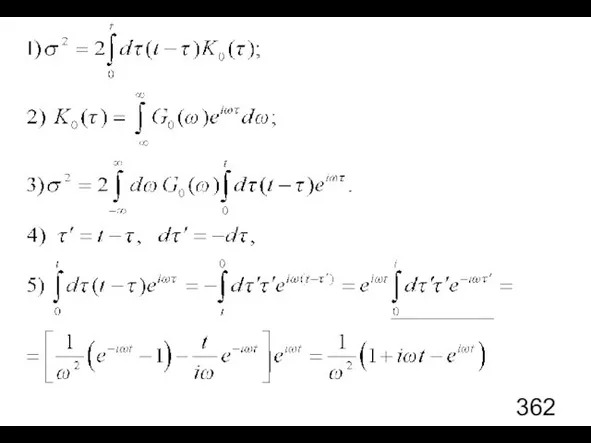












![Модели случайных процессов (план) см [1]. Глава 2 Спектральный анализ](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/36579/slide-103.jpg)





















 Путешествие по родному краю. Конкурсы
Путешествие по родному краю. Конкурсы Курсовое проектирование как одна из форм подготовки конкурентоспособного специалиста
Курсовое проектирование как одна из форм подготовки конкурентоспособного специалиста Развитие социологии (до 1940-х гг.)
Развитие социологии (до 1940-х гг.) American history
American history Презентация Открытка к 8 марта
Презентация Открытка к 8 марта Технологиялық машиналар және жабдықтар
Технологиялық машиналар және жабдықтар Итоговое сочинение. Критерии оценивания
Итоговое сочинение. Критерии оценивания Проектная задача Буклет для дошкольника
Проектная задача Буклет для дошкольника Лазерная физика. Основные задачи курса
Лазерная физика. Основные задачи курса Буровые растворы. Бурение нефтяных и газовых скважин
Буровые растворы. Бурение нефтяных и газовых скважин Ранние формы религии. Часть I
Ранние формы религии. Часть I Анализ аптечного ассортимента лекарственного растительного сырья, содержащего эфирные масла и препаратов из него
Анализ аптечного ассортимента лекарственного растительного сырья, содержащего эфирные масла и препаратов из него Машины для противоэрозионной обработки почв
Машины для противоэрозионной обработки почв Урок химии в 8 классе Обобщающее повторение по теме сложные вещества
Урок химии в 8 классе Обобщающее повторение по теме сложные вещества Транспортная логистика. (Раздел 2.3)
Транспортная логистика. (Раздел 2.3) Психолого-педагогическое сопровождение семьи, воспитывающей ребенка раннего и дошкольного возраста
Психолого-педагогическое сопровождение семьи, воспитывающей ребенка раннего и дошкольного возраста Строительство поверхностной обработки покрытий
Строительство поверхностной обработки покрытий Doping-legalization
Doping-legalization Русская народная сказка Теремок
Русская народная сказка Теремок красивая речь ребенка
красивая речь ребенка Значение и перспективы развития тары и упаковки в управлении товародвижением в компании “СПСР экспресс”
Значение и перспективы развития тары и упаковки в управлении товародвижением в компании “СПСР экспресс” Давление. 7 класс
Давление. 7 класс Une petite histoire
Une petite histoire Военнослужащие и взаимоотношения между ними
Военнослужащие и взаимоотношения между ними Морфофункциональная характеристика скелета и аппарата движения нижних конечностей человека
Морфофункциональная характеристика скелета и аппарата движения нижних конечностей человека Медиация равных
Медиация равных род.собрание
род.собрание Смешанное вскармливание. Лекция
Смешанное вскармливание. Лекция