Содержание
- 2. Палочка – выручалочка Квадраты чисел 8² 14² 35², 65² 53² = ? 1. 3²=9 - последняя
- 3. Преобразования подкоренного выражения Вычислите квадратные корни из дискриминанта квадратных уравнений: а) 5х²-101х+20=0 б) 8х²+49х-49=0
- 4. Большое значение теории квадратных уравнений в развитии математической науки подтверждается, тем, что математики всех древних цивилизаций
- 5. За страницами учебника Способ “переброски” старшего коэффициента Рассмотрим квадратное уравнение ах² + bх + с =
- 6. Способ “переброски” старшего коэффициента 4х2 + 15х + 11 = 0. Решение. у2 + 15y +44
- 7. Мухаммед бен Муса аль-Хорезми АЛЬ-ХОРЕЗМИ (786—850 гг.), персидский математик. Его научные интересы касались математики, астрономии, географии.
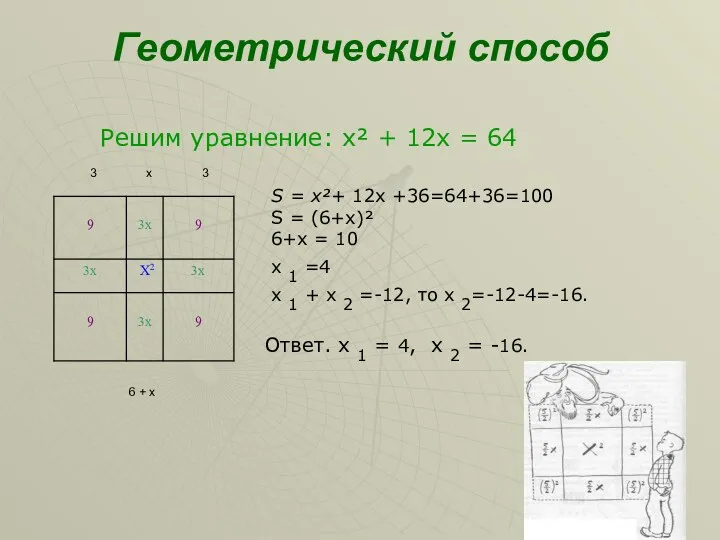
- 8. Геометрический способ 3 х 3 6 + х Решим уравнение: х² + 12х = 64 S
- 9. Логическая пауза Трактат аль-Хорезми «Книга о восстановлении и противопоставлении» - это первая книга, в которой изложена
- 10. Составьте уравнение: а) три квадрата равны 9-ти корням, б) четыре корня и 25 равны 6-ти квадратам,
- 11. Способ решения квадратных уравнений «Пять шагов» Решим уравнение: х² +15=8х. Шаги: 1. 8:2=4 2. 4*4=16 3.
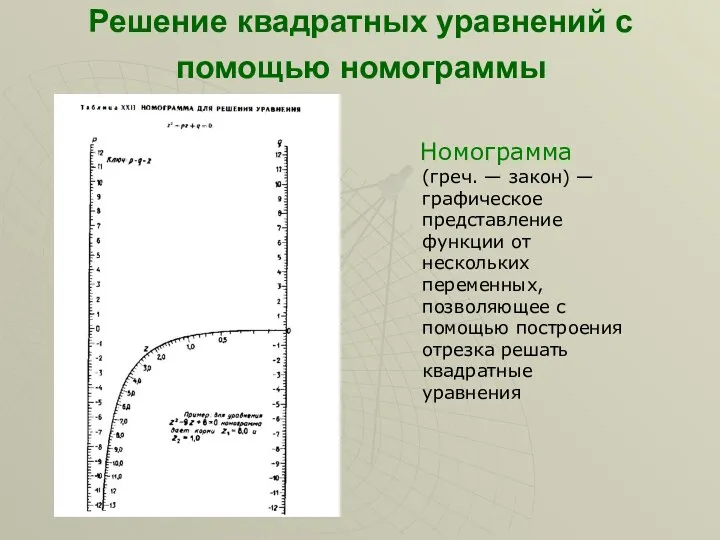
- 12. Решение квадратных уравнений с помощью номограммы Номограмма (греч. — закон) — графическое представление функции от нескольких
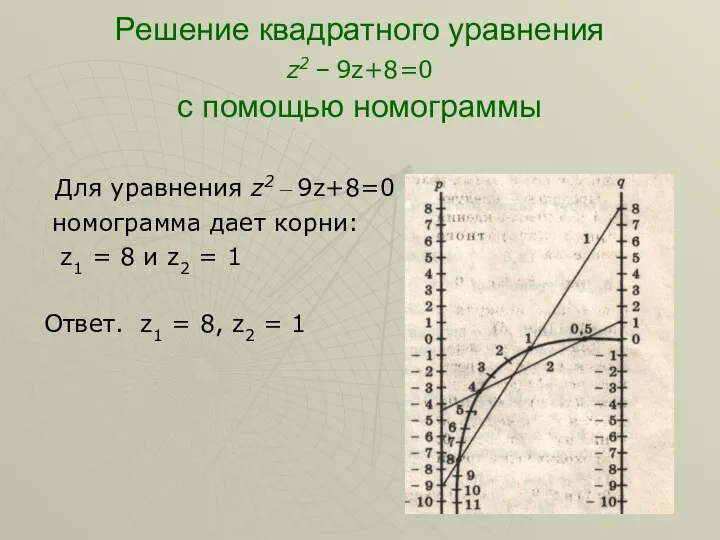
- 13. Решение квадратного уравнения z2 – 9z+8=0 с помощью номограммы Для уравнения z2 – 9z+8=0 номограмма дает
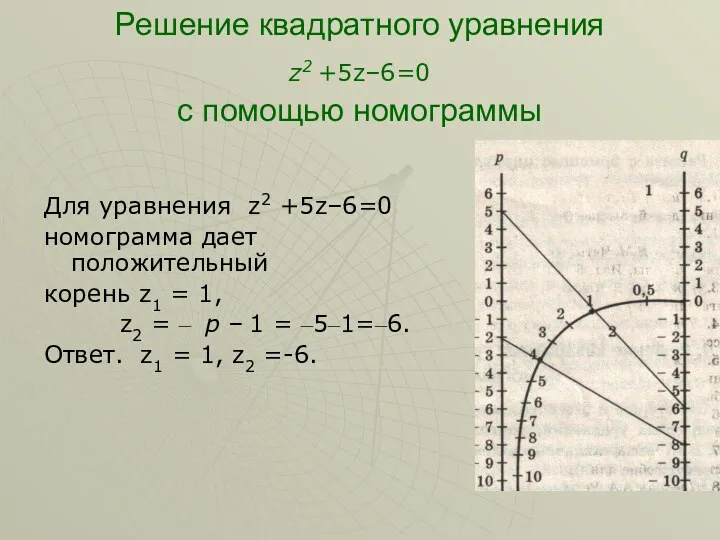
- 14. Решение квадратного уравнения z2 +5z–6=0 с помощью номограммы Для уравнения z2 +5z–6=0 номограмма дает положительный корень
- 16. Скачать презентацию









 Делимость чисел 6 класс. Презентация для интерактивной доски
Делимость чисел 6 класс. Презентация для интерактивной доски Умножение чисел с разными знаками
Умножение чисел с разными знаками Конспект и технологическая карта урока по теме Арифметическая прогрессия Технологическая карта урока (учебного занятия) на основе системно-деятельностного подхода.
Конспект и технологическая карта урока по теме Арифметическая прогрессия Технологическая карта урока (учебного занятия) на основе системно-деятельностного подхода.  15 февраля в истории Кубани. Сложение и вычитание десятичных дробей.
15 февраля в истории Кубани. Сложение и вычитание десятичных дробей. Презентации по математике - 6 класс
Презентации по математике - 6 класс Тест Обыкновенные дроби 5 класс
Тест Обыкновенные дроби 5 класс презентации по курсу занимательная математика
презентации по курсу занимательная математика Презентация Разложение на множители, конспект урока алгебры 7 класс, раздаточный материал
Презентация Разложение на множители, конспект урока алгебры 7 класс, раздаточный материал Своя игра Сложение и вычитание дробей
Своя игра Сложение и вычитание дробей Показательная функция, ее свойства и график( тест)
Показательная функция, ее свойства и график( тест) Повышение учебной мативации школьников на уроках математики.
Повышение учебной мативации школьников на уроках математики. Внеклассное мероприятие по математикеЗвездный час.
Внеклассное мероприятие по математикеЗвездный час. использование икт в учебном процессе
использование икт в учебном процессе Материал к ЕГ (повышенный уровень сложности) на 3 б
Материал к ЕГ (повышенный уровень сложности) на 3 б Презентация к уроку в 6 классе по теме Координатная плоскость
Презентация к уроку в 6 классе по теме Координатная плоскость Зигзаг удачи!
Зигзаг удачи! Элективные курсы по математике Процентные расчёты на каждый день.
Элективные курсы по математике Процентные расчёты на каждый день. Арифметическая и геометрическая прогрессии
Арифметическая и геометрическая прогрессии Сложение и вычитание одночленов
Сложение и вычитание одночленов 9 класс. Дробные рациональные уравнения.
9 класс. Дробные рациональные уравнения. В царстве математики
В царстве математики Презентация Обыкновенные дроби. Часть 2. 5 класс
Презентация Обыкновенные дроби. Часть 2. 5 класс ДЛФ
ДЛФ Решение тригонометрических неравенств 10 класс ( профиль)
Решение тригонометрических неравенств 10 класс ( профиль) Конспект урока математики 5 класс Все действия с натуральными числами
Конспект урока математики 5 класс Все действия с натуральными числами Презентация. Повторение по теме: Деление обыкновенныхдробей
Презентация. Повторение по теме: Деление обыкновенныхдробей Совместные действия с алгебраическими дробями. Умножение и деление алгебраических дробей.
Совместные действия с алгебраическими дробями. Умножение и деление алгебраических дробей. Презентация урока Определение вероятности
Презентация урока Определение вероятности