Содержание
- 2. 1. Теоретическая разминка. 2. Тест. 3. Практикум. 4. Историческая справка. 5. Презентация специальных методов решения квадратных
- 3. Термин «квадратное уравнение» впервые ввёл Кристиан Вольф Кристиан Вольф - знаменитый немецкий философ. Родился в 1679
- 4. Английский математик, который ввёл термин «дискриминант». Сильвестр Джеймс Джозеф
- 5. В 13 – 16 веках даются отдельные методы решения различных видов квадратных уравнений. Слияние этих методов
- 6. Уравнение какого вида называют квадратным? Как по названиям различают коэффициенты а, в и с? Объясните, в
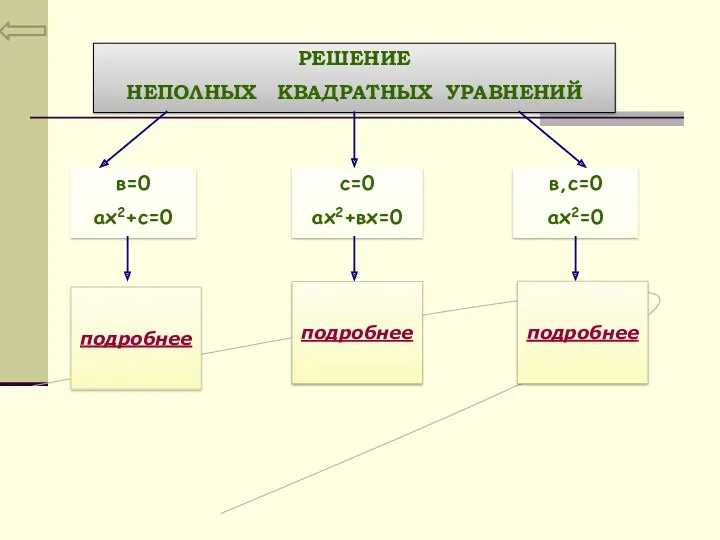
- 7. Неполные квадратные уравнения
- 8. РЕШЕНИЕ НЕПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙ в=0 ах2+с=0 с=0 ах2+вх=0 в,с=0 ах2=0 подробнее подробнее подробнее
- 9. Алгоритм решения 1.Переносим с в правую часть уравнения. ах2 = -с. 2. Делим обе части уравнения
- 10. Выносим x за скобки: х (ах + в) = 0. 2. «Разбиваем» уравнение на два: x
- 11. 1. Делим обе части уравнения на а≠0. х2 = 0 2. Одно решение: х = 0.
- 12. D Корней нет D = 0 D > 0
- 13. b = 2k (четное число)
- 14. Специальные методы Метод выделения квадрата двучлена Метод «переброски» старшего коэффициента На основании теорем
- 15. Цель: привести квадратное уравнение общего вида к неполному квадратному уравнению. Пример: Метод выделения квадрата двучлена Х2
- 16. Метод выделения квадрата двучлена (a + b)2 = a2 + 2ab + b2, (a - b)2
- 17. Корни квадратных уравнений и связаны соотношениями и В некоторых случаях бывает удобно решать сначала не данное
- 18. Метод “переброски” старшего коэффициента ax2 + bx + c = 0 и y2+ by + ac
- 19. На основании теорем: 1. Если в квадратном уравнении a+b+c=0, то один из корней равен 1, а
- 20. Теорема 1. Если в квадратном уравнении a + b + c = 0, то один из
- 21. Теорема 2. Если в квадратном уравнении a + c = b, то один из корней равен
- 22. Общие методы Разложение на множители; Введение новой переменной; Графический метод.
- 23. Метод разложения на множители привести квадратное уравнение общего вида к виду А(х)·В(х)=0, где А(х) и В(х)
- 24. Решите уравнение 4х2 + 5х + 1 = 0. 4х2 + 5х + 1 = 0.
- 25. Введение новой переменной. Умение удачно ввести новую переменную – важный элемент математической культуры. Удачный выбор новой
- 26. Метод введения новой переменной Решите уравнение (2х+3)2 = 3(2х+3) – 2. (2х+3)2 = 3(2х+3) – 2.
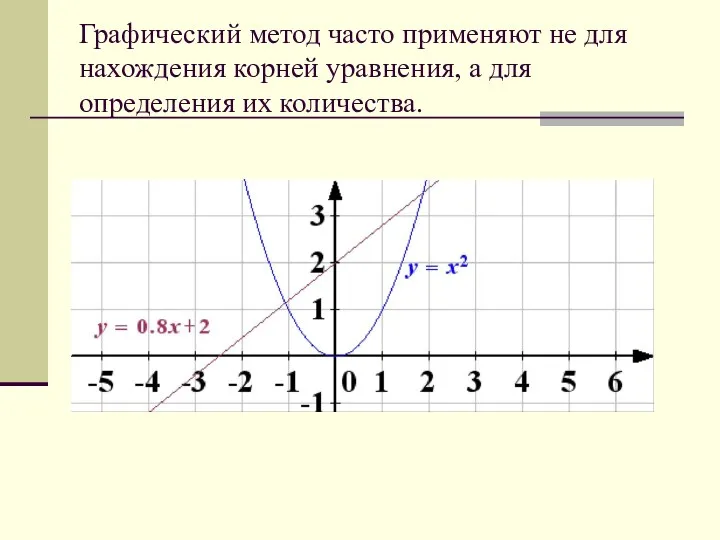
- 27. Графический метод Для решения уравнения f(x) = g(x) необходимо построить графики функций y = f(x), y
- 28. Графический метод часто применяют не для нахождения корней уравнения, а для определения их количества.
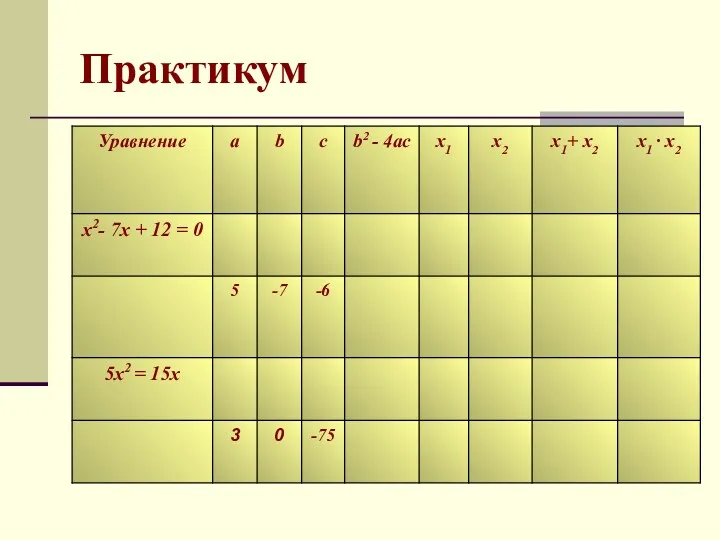
- 29. Практикум
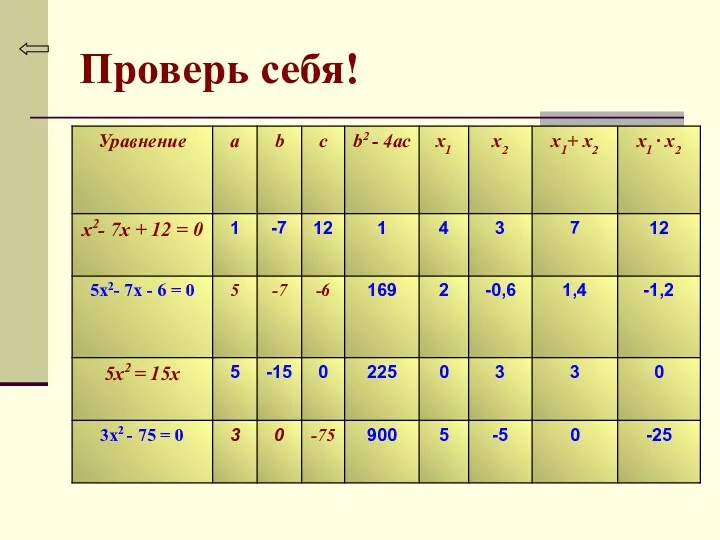
- 30. Проверь себя!
- 31. ТЕСТ
- 33. Скачать презентацию










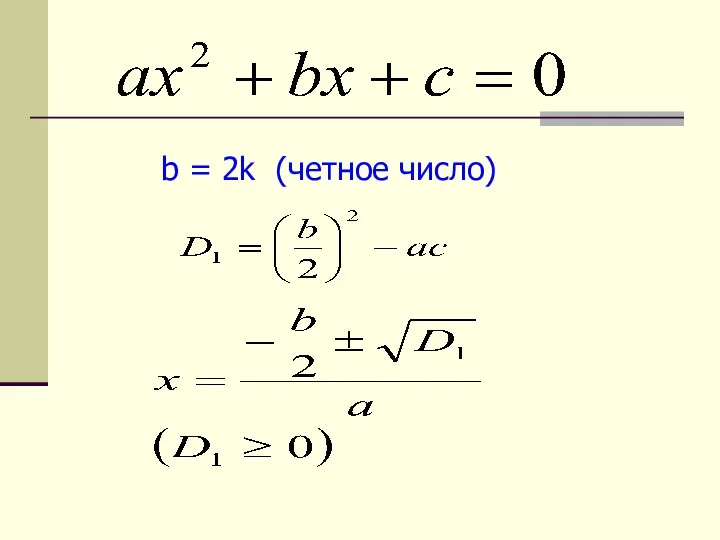















 Однородные тригонометрические уравнения, 10 класс
Однородные тригонометрические уравнения, 10 класс конспект урока Порядок выполнения действий
конспект урока Порядок выполнения действий Математическая регата
Математическая регата Обыкновенные дроби
Обыкновенные дроби Урок математики с психологическим сопровождением
Урок математики с психологическим сопровождением История возникновения логарифмов алгебра 10 класс
История возникновения логарифмов алгебра 10 класс Сравнение десятичных дробей
Сравнение десятичных дробей эколого - математический брейн -ринг
эколого - математический брейн -ринг Терема Виета
Терема Виета разработка урока Умножение рациональных чисел, математика 6 класс (уч Виленкин Н.Я.)
разработка урока Умножение рациональных чисел, математика 6 класс (уч Виленкин Н.Я.) Определение логарифма. Презентация
Определение логарифма. Презентация компьютерная презентация к уроку в 5 классе по теме Числовые и буквенные выражения
компьютерная презентация к уроку в 5 классе по теме Числовые и буквенные выражения Округление чисел
Округление чисел Уравнения и неравенства с одной переменной.
Уравнения и неравенства с одной переменной. Решение уравнений в среде табличного процессора Excel.
Решение уравнений в среде табличного процессора Excel. Что такое разложение на множители и зачем оно нужно
Что такое разложение на множители и зачем оно нужно внеклассное мероприятие Математический аукцион
внеклассное мероприятие Математический аукцион презентация к уроку Последовательности Диск
презентация к уроку Последовательности Диск Раскрытие скобок 6 класс
Раскрытие скобок 6 класс Презентация по теме Координаты на плоскости, часть 2 Координатная плоскость
Презентация по теме Координаты на плоскости, часть 2 Координатная плоскость Мультимедийный урок-игра по теме Системы линейных уравнений
Мультимедийный урок-игра по теме Системы линейных уравнений Процент
Процент степень с целым показателем. 8 класс
степень с целым показателем. 8 класс Готовимся к ЕГЭ
Готовимся к ЕГЭ Квадратичная функция
Квадратичная функция Задачи на части
Задачи на части Приведение подобных радикалов
Приведение подобных радикалов Элективный курс Рациональные уравнения и неравенства
Элективный курс Рациональные уравнения и неравенства