Содержание
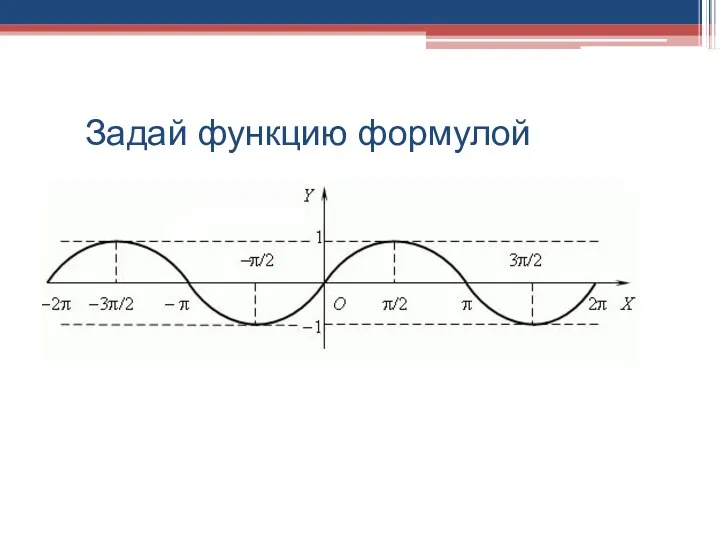
- 2. Задай функцию формулой
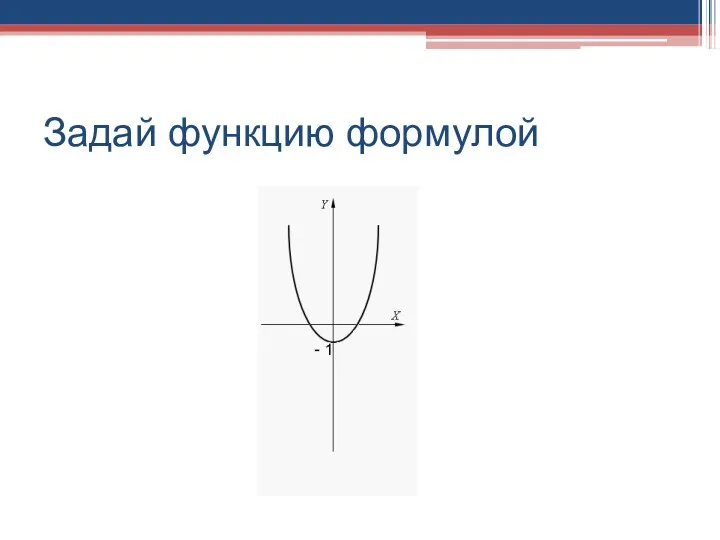
- 3. Задай функцию формулой
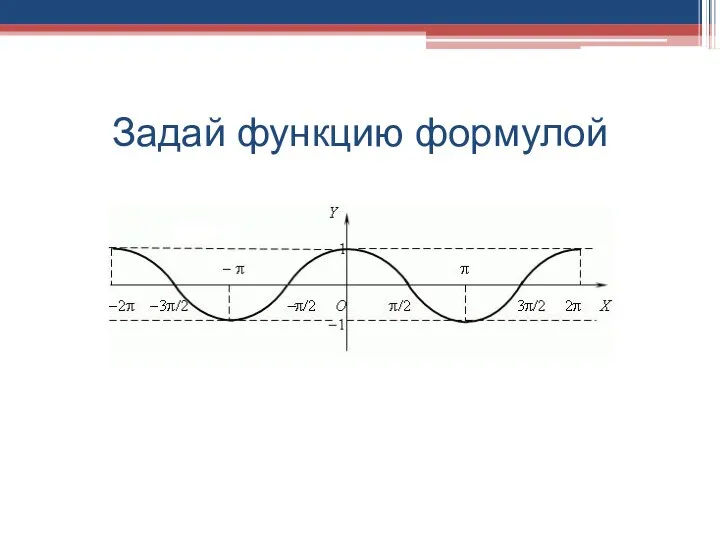
- 4. Задай функцию формулой
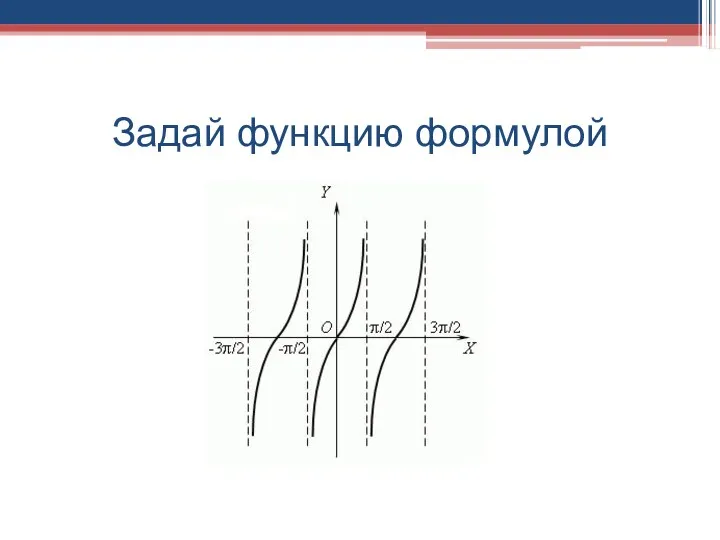
- 5. Задай функцию формулой
- 6. Задай функцию формулой
- 7. Задай функцию формулой
- 8. Задай функцию формулой
- 9. Задай функцию формулой
- 10. Задай функцию формулой
- 16. . Выполнила ученица 10 «А» Засыпалова Анна Как построить график функции y=f(|x|).
- 17. Правило построения графика функции y=f(|x|). : 1. Построим график функции y=f(x), для х≥0 2. Достроим левую
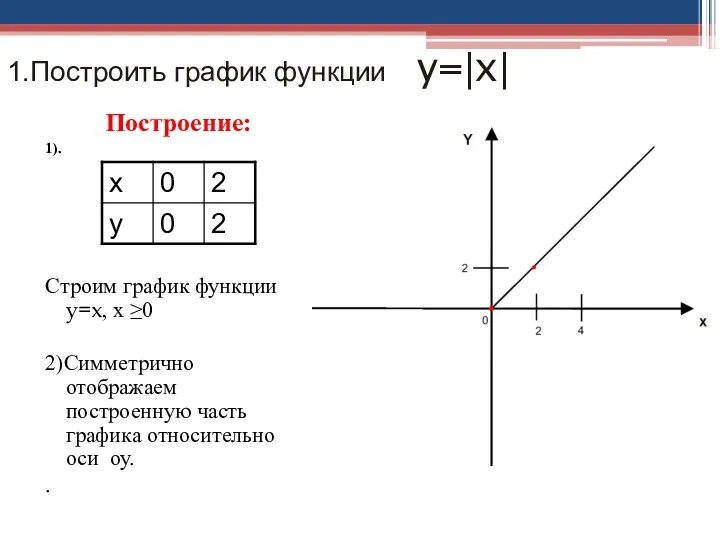
- 18. 1.Построить график функции y=|x| Построение: 1). Строим график функции y=x, х ≥0 2)Симметрично отображаем построенную часть
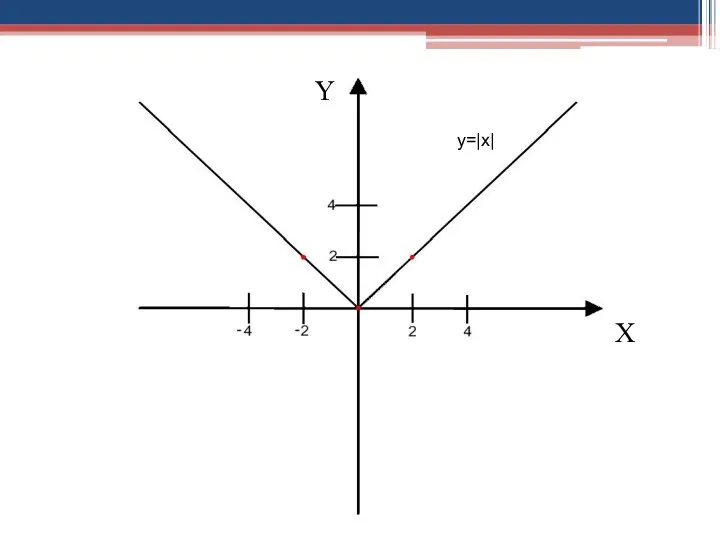
- 19. Y y=|x| X
- 20. 2. Построить график функции Y=|x|²-4|x|+3 Построение. 1)Строим y=x²-4x+3, х≥0 а)Хверш= -в/2а=-4/2=2 Уверш=2²-4·2+3=-1 (2;-1)-вершина параболы б)Нули функции
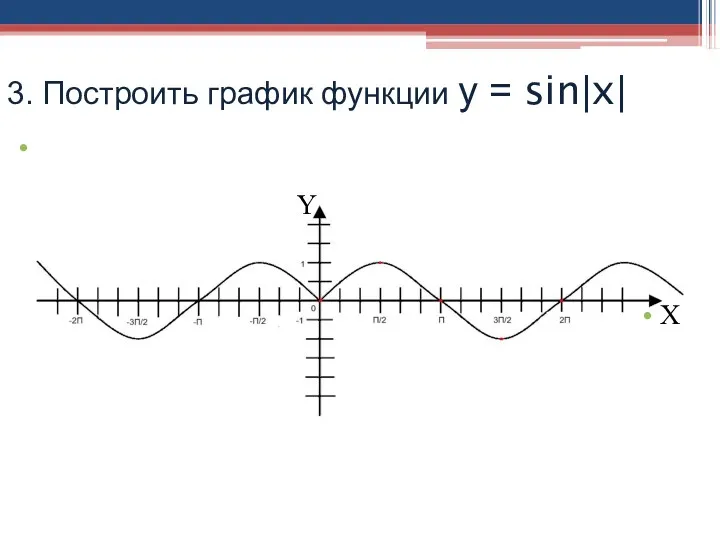
- 21. 3. Построить график функции у = sin|x| Y X
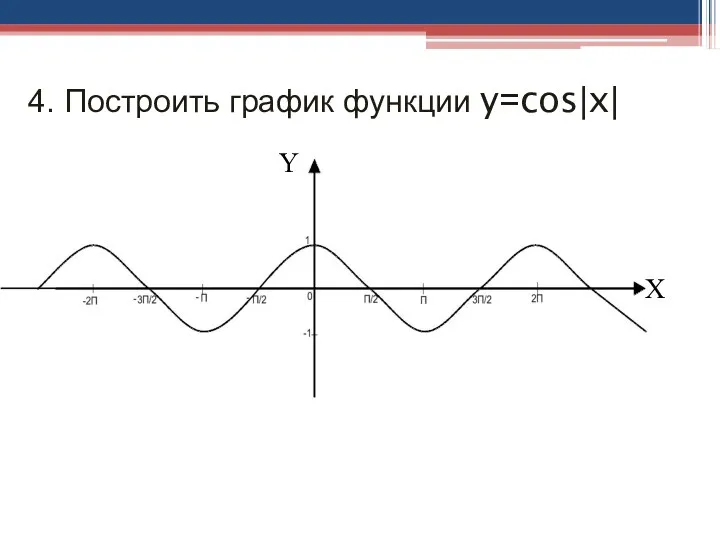
- 22. 4. Построить график функции y=cos|x| Y X
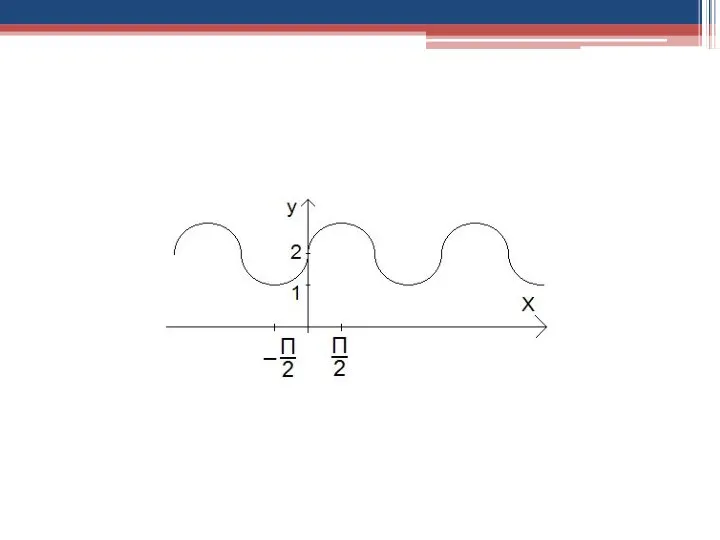
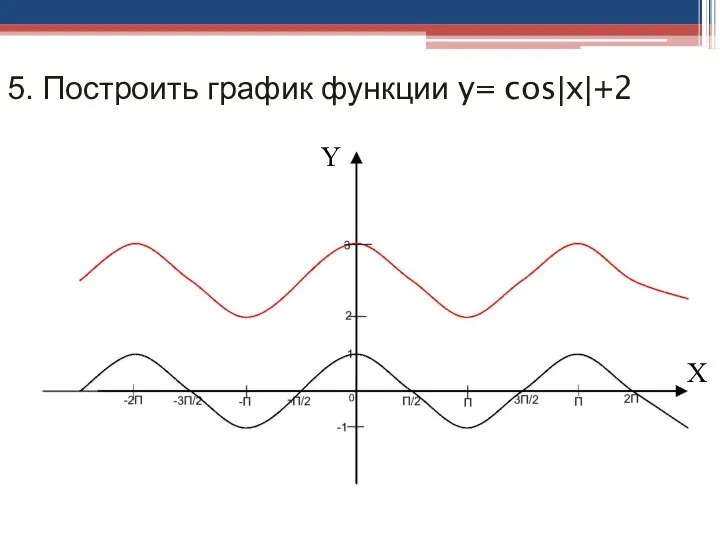
- 23. 5. Построить график функции y= cos|x|+2 Y X
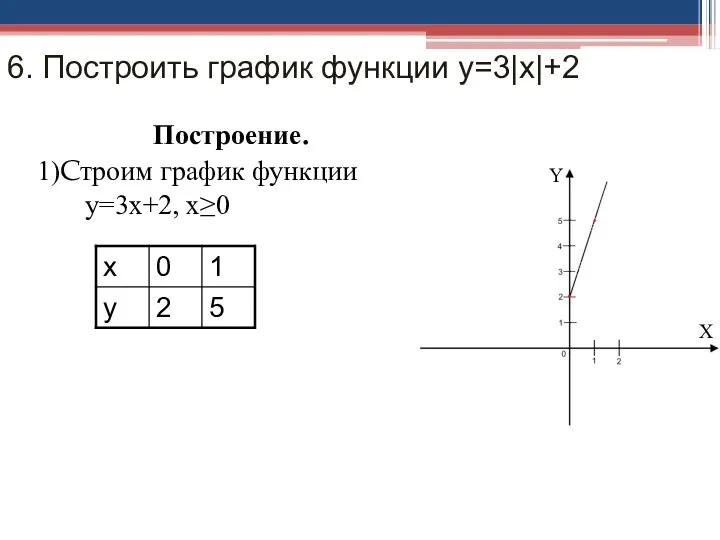
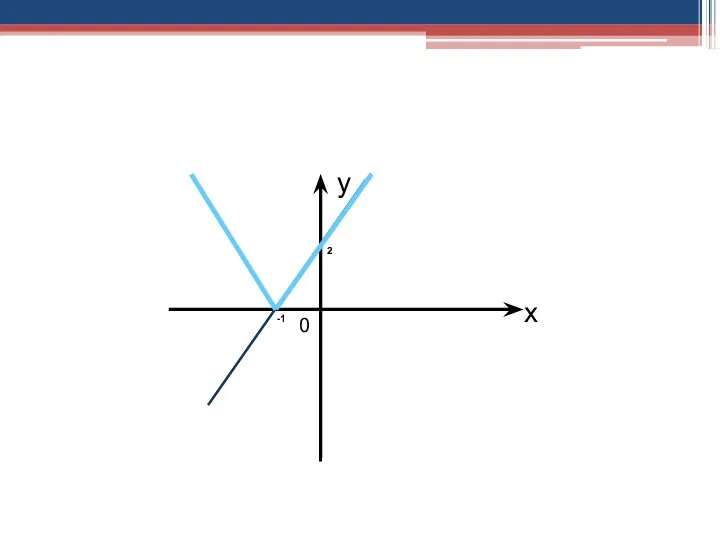
- 24. 6. Построить график функции у=3|х|+2 Построение. 1)Cтроим график функции у=3х+2, х≥0 Y X
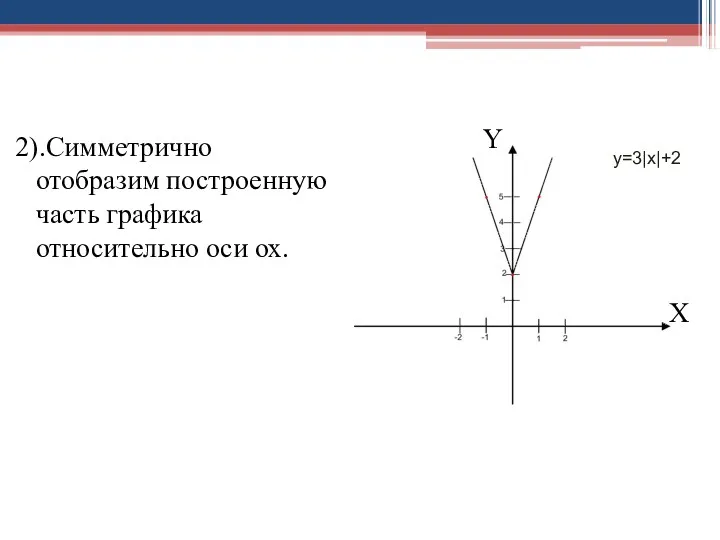
- 25. 2).Симметрично отобразим построенную часть графика относительно оси ох. у=3|х|+2 Y X
- 26. Выполнила: Кузьмина Валерия ученица 10 «а» класса
- 27. ПРАВИЛО ПОСТРОЕНИЯ ГРАФИКА ФУНКЦИИ Y=|F(X)| 1.Построить график y=f(x) 2.Сохранить без изменения части графика y=f(x), расположенные выше
- 28. 1).ПОСТРОИТЬ ГРАФИК ФУНКЦИИ Y=|3X+2| ПОСТРОЕНИЕ. 1. ПОСТРОИМ ГРАФИК ФУНКЦИИ Y=3X+2. 2. ЧАСТЬ ГРАФИКА, РАСПОЛОЖЕННУЮ НИЖЕ ОСИ
- 29. x y 0 2 -1
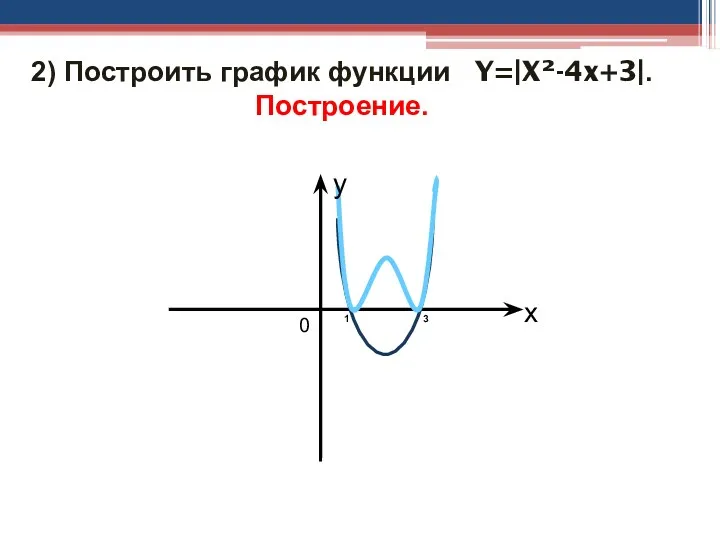
- 30. 2) Построить график функции Y=|X²-4x+3|. Построение. y x 0 1 3
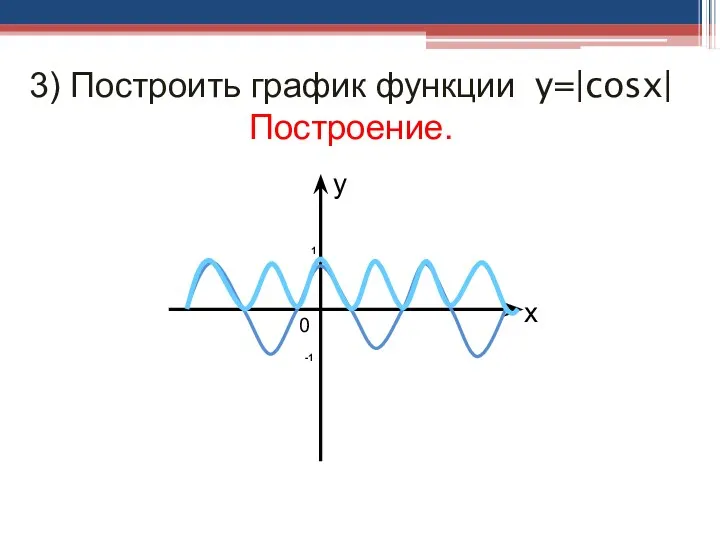
- 31. 3) Построить график функции y=|cosx| Построение. 0 y x 1 -1
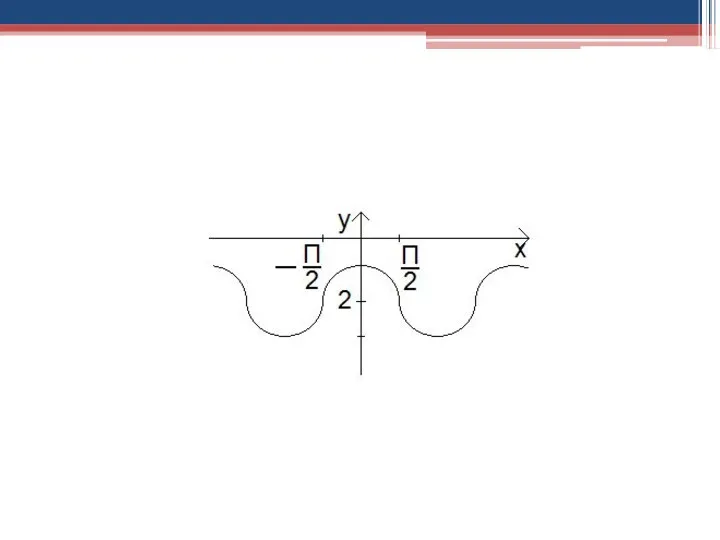
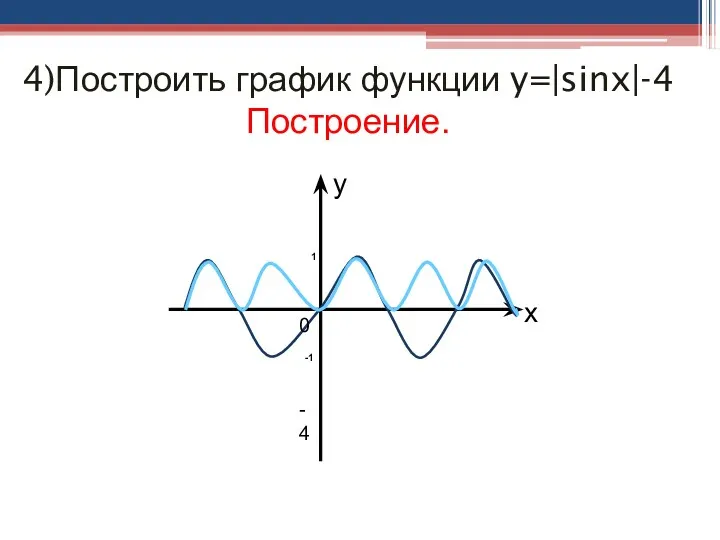
- 32. 4)Построить график функции y=|sinx|-4 Построение. 0 y x -4 1 -1
- 33. Решение уравнений, содержащих модуль
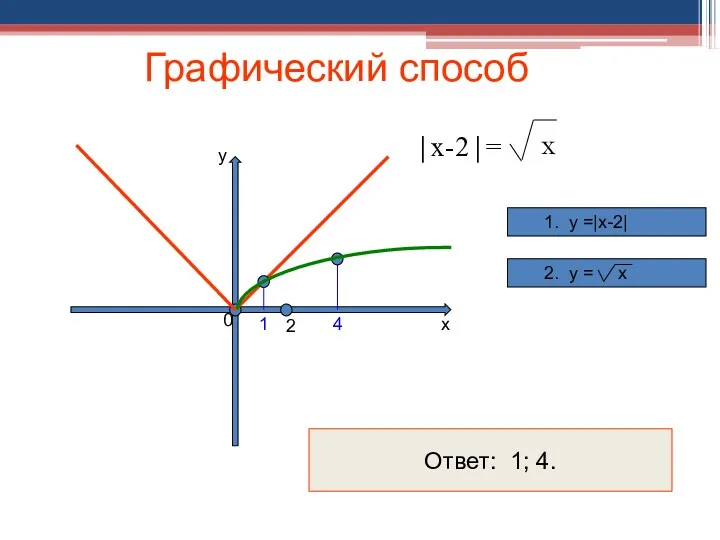
- 35. Графический способ |х-2|= 2 х у 0 4 1 х 1. у =|х-2| 2. у =
- 36. Задания командам Реши уравнение графическим способом а) |x-1|=2; б) x2 = |x|; в)sin|x| = - х2;
- 41. Итоги
- 42. ИСТОРИЧЕСКАЯ СПРАВКА
- 43. Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Это многозначное слово(омоним), которое
- 44. Модуль числа Абсолютная величина или модуль, обозначается |x|, |x-1| , |a|
- 45. Знак модуля Считают, что термин предложил использовать Котс, ученик Ньютона. Лейбниц тоже использовал эту функцию, которую
- 46. Математики шутят. Трехмерная кубическая линейка
- 48. Калькулятор для умных
- 50. Скачать презентацию























 Презентация на открытый урок 5 класс по ФГОС Сложение и вычитание натуральных чисел
Презентация на открытый урок 5 класс по ФГОС Сложение и вычитание натуральных чисел игра для учащихся старших классов Морской бой
игра для учащихся старших классов Морской бой Вычисление площади фигур на клетчатой бумаге. Диск
Вычисление площади фигур на клетчатой бумаге. Диск Презентация к уроку математики Коэффициент (6класс)
Презентация к уроку математики Коэффициент (6класс) Презентация к уроку обобщения и систематизации по теме: Квадратные уравнения: Решение задач с помощью квадратных уравнений
Презентация к уроку обобщения и систематизации по теме: Квадратные уравнения: Решение задач с помощью квадратных уравнений Путешествие к острову обыкновенных дробей 5 класс
Путешествие к острову обыкновенных дробей 5 класс Презентация урока Сравнение дробей, 5 класс
Презентация урока Сравнение дробей, 5 класс Тест сложение рациональных чисел
Тест сложение рациональных чисел Презентация Квадратные неравенства
Презентация Квадратные неравенства План-конспект урока Квадратные уравнения
План-конспект урока Квадратные уравнения Деление. Задачи на движение
Деление. Задачи на движение Своя игра
Своя игра Алгебраические дроби
Алгебраические дроби Степенная функция. 9 класс.
Степенная функция. 9 класс. смешанные числа Тема урока: Смешанные числа Класс: 5 Дидактическая цель: создать условия для формирования новой учебной информации. Цели по содержанию: - развивающие: развивать умения анализировать, сравнивать, обобщать, делать выводы, развивать вни
смешанные числа Тема урока: Смешанные числа Класс: 5 Дидактическая цель: создать условия для формирования новой учебной информации. Цели по содержанию: - развивающие: развивать умения анализировать, сравнивать, обобщать, делать выводы, развивать вни урок по математике в 9 классе
урок по математике в 9 классе Материал для подготовки к ОГЭ модуль Геометрия
Материал для подготовки к ОГЭ модуль Геометрия Различные способы решения задач с параметрами.
Различные способы решения задач с параметрами. Возведение в квадрат суммы и разности двух выражений
Возведение в квадрат суммы и разности двух выражений Презентация Показательные уравнения
Презентация Показательные уравнения Пифагор
Пифагор Открытый урок в 11 классе Решение логарифмических уравнений - поиск ошибок
Открытый урок в 11 классе Решение логарифмических уравнений - поиск ошибок внеклассное мероприятие по математике в разновозрастной группе по теме Проценты
внеклассное мероприятие по математике в разновозрастной группе по теме Проценты Задача на проценты
Задача на проценты Системы тригонометрических уравнений
Системы тригонометрических уравнений Упрощение выражений 5 класс
Упрощение выражений 5 класс Открытый урок по математике Дробные выражения
Открытый урок по математике Дробные выражения Презентация к уроку математики в 5 классе: Правильные и неправильные дроби
Презентация к уроку математики в 5 классе: Правильные и неправильные дроби