Содержание
- 2. Домашнее задание: 1)Найдите сумму корней уравнения | (x-2)3 -140| =76. 2)Укажите наибольшее решение уравнения | |1-2x|-1|=0.
- 3. Систематизировать знания по теме «Уравнения»: повторить рациональные уравнения, их виды, способы решения. Проверить: навыки решения квадратных
- 4. Равносильность уравнений.
- 5. Основные определения. 1. Два уравнения f1(x) = g1(x) и f2(x) = g2(x) называются равносильными, если они
- 6. Теоремы о равносильности уравнений. Теорема 1. Если какой-нибудь член уравнения перенести из одной части уравнения в
- 7. Рациональные уравнения.
- 8. Основные определения. Уравнение, левая и правая части которого есть рациональные выражения относительно Х ,называют рациональными уравнениями
- 9. Уравнение вида А(х)В(х)=0, где А(х), В(х) – многочлены относительно х , называются распадающимся уравнением. 2. Уравнение
- 10. 1. Решите уравнение(х2-5х+6) (х2+ х-2). Ответ: -2; 1; 2; 3 2. Решите уравнение Решение: а)Сначала решим
- 11. 3. Решите уравнение а) решим уравнение х2 + 2х- 15 = 0; х1= - 5; х2
- 12. Алгоритмы решения уравнений,содержащих переменную под знаком модуля.
- 13. Определение Модулем (абсолютной величиной) действительного числа а называют неотрицательное действительное число, определяемое равенством Модуль – это
- 14. Основные свойства модуля. 1 2 3 5 | а| ≥ 0 | а|=| - а| |
- 15. Раскройте модуль:.
- 16. Алгоритм решения уравнения | f (x)| = а , а ∈ R . 1) Если а
- 17. Решить уравнения. 1 2 3 | 2x – 3 | + 11 = 0, | 2x
- 18. Преподаватели математики Хохлова С.Н., Мещенко Н.В.
- 19. Проверка домашней работы 1) | (x-2)3 -140| =76. Решение: Ответ: 6; 8. 2) Решите | |1-2x|-1|=0.
- 20. 3) Решите | |x-6|-6|=6. Решение: Ответ: -6; 6; 18. 4)Сколько решений может иметь уравнение |x-12|=a2-5a+6 в
- 21. Алгоритм решения уравнения| f (x)| = | ϕ (x)| 1 способ |f (x)| = |ϕ (x)|,
- 22. 1 способ 2|x + 1| = |3 – x|, (2|x + 1 |)2 = |3 –
- 23. Алгоритм решения уравнения | f (x)| = ϕ (x) . 1 способ. Воспользуемся определением модуля. 2
- 24. Пример 1. Решить уравнение | 2 – х | = 1 – 2х. х = –
- 25. Пример 2. Решить уравнение |х2 + 3х – 4| = 3х. Ответ: Решение.
- 26. Цель урока: формирование знаний и умений решения уравнений вида |f1 (x)| + |f2 (x)| +| f3
- 27. План урока: Проверка домашнего задания. Объяснение нового материала. Закрепление нового материала. Закрепление навыков решения уравнений (самостоятельная
- 28. «Цветик-семицветик» Повторим теорию
- 29. Сформулируйте определение модуля действительного числа. Раскройте модуль выражений: а) 2⋅|4 - х|, б) |у + 3|
- 30. Сколько решений имеет уравнение |х| = а в зависимости от а?. Приведите примеры уравнений вида |7-
- 31. Алгоритм решения уравнения |f1 (x)| + |f2 (x)| + | f3 (x)| + … + |
- 32. Пример 1. Решить уравнение | х – 2 | + | х + 1 | =
- 33. – 1 ≤ x х = 2. – 1 ≤ x ≤ 2, Ответ: [ -
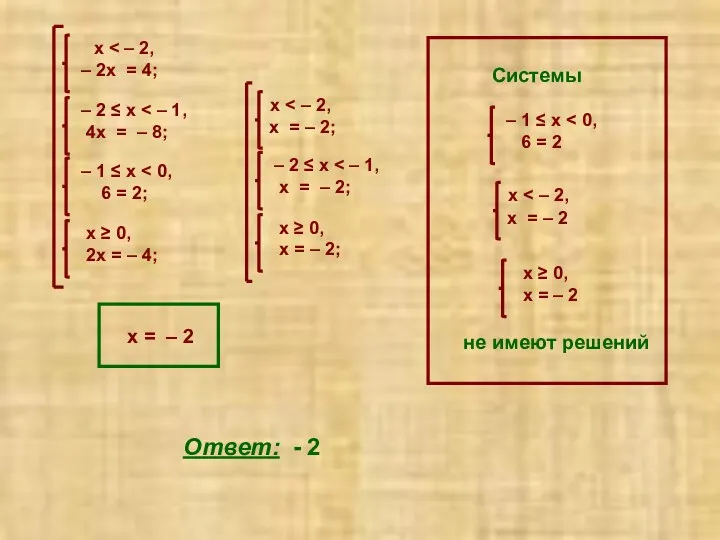
- 34. Пример 2. Решить уравнение | х | + 3| х + 2 | = 2 |
- 35. Системы не имеют решений х = – 2 Ответ: - 2
- 36. Преподаватели математики Хохлова С.Н., Мещенко Н.В.
- 37. Алгоритмы решения уравнений |f (x)| = f (x) , |f (x)| = – f (x) и
- 38. 1 Найти меньший целый корень уравнения. | 3x – 5 | = 3х – 5 ,
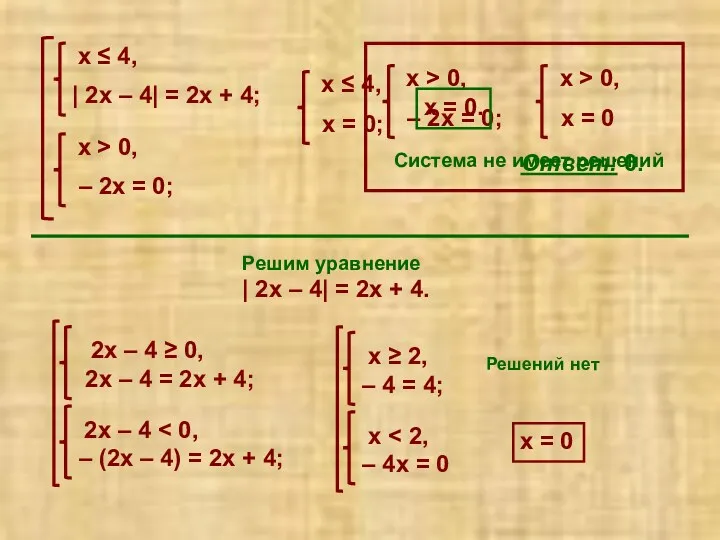
- 39. Решение уравнений, в которых под знаком модуля находится выражение, содержащее модуль. Сначала следует освободиться от внутреннего
- 40. Система не имеет решений Решим уравнение | 2х – 4| = 2х + 4. Решений нет
- 41. Решение уравнений вида а ⋅f 2(x) + b⋅ |f (x)| + c = 0 . Так
- 43. Скачать презентацию






































 Презентация к уроку Уравнения
Презентация к уроку Уравнения Урок повторения и систематизации знаний по теме: Одночлены и многочлены 7 класс. Проводится в занимательной игровой форме: Путешествие в мир Одночленов и Многочленов.
Урок повторения и систематизации знаний по теме: Одночлены и многочлены 7 класс. Проводится в занимательной игровой форме: Путешествие в мир Одночленов и Многочленов. Олимпиадные задачи для пятиклассников №1
Олимпиадные задачи для пятиклассников №1 Презентация к уроку математики по теме Сложение и вычитание десятичных дробей
Презентация к уроку математики по теме Сложение и вычитание десятичных дробей Использование интерактивной доски на уроках математики
Использование интерактивной доски на уроках математики Технология модульного обучения
Технология модульного обучения Мультимедийный урок-игра по теме Системы линейных уравнений
Мультимедийный урок-игра по теме Системы линейных уравнений Практикум Умножение и деление десятичных дробей
Практикум Умножение и деление десятичных дробей Урок алгебры в 7 классе Среднее арифметическое, размах и мода
Урок алгебры в 7 классе Среднее арифметическое, размах и мода Умножение десятичных дробей на натуральные числа
Умножение десятичных дробей на натуральные числа ЦОР Задачи на движение
ЦОР Задачи на движение Урок Округление чисел - 5 класс
Урок Округление чисел - 5 класс Урок Разложение многочлена на множители
Урок Разложение многочлена на множители Презентация и конспект урока по математике в 6 классе Окружность. Длина окружности
Презентация и конспект урока по математике в 6 классе Окружность. Длина окружности Этап актуализации знаний 5 класс сравнение дробей
Этап актуализации знаний 5 класс сравнение дробей Устный счет по теме Десятичные дроби, 5 класс
Устный счет по теме Десятичные дроби, 5 класс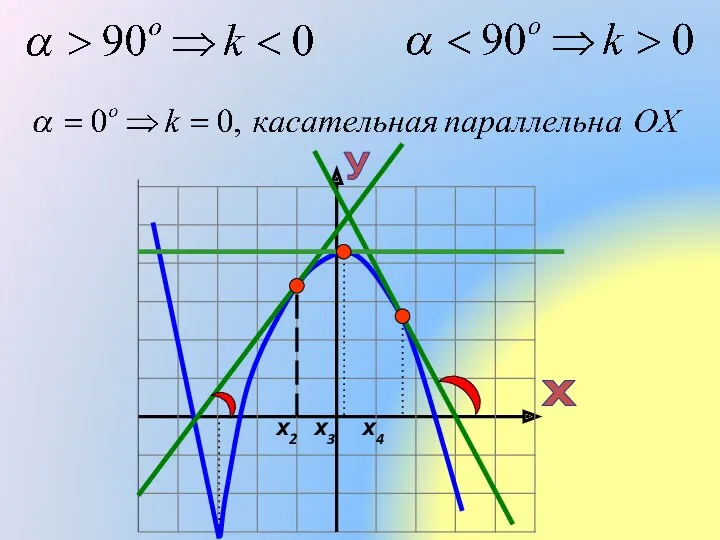 Задачи о касательной
Задачи о касательной Преобразование графиков функций
Преобразование графиков функций Законы арифметических действий
Законы арифметических действий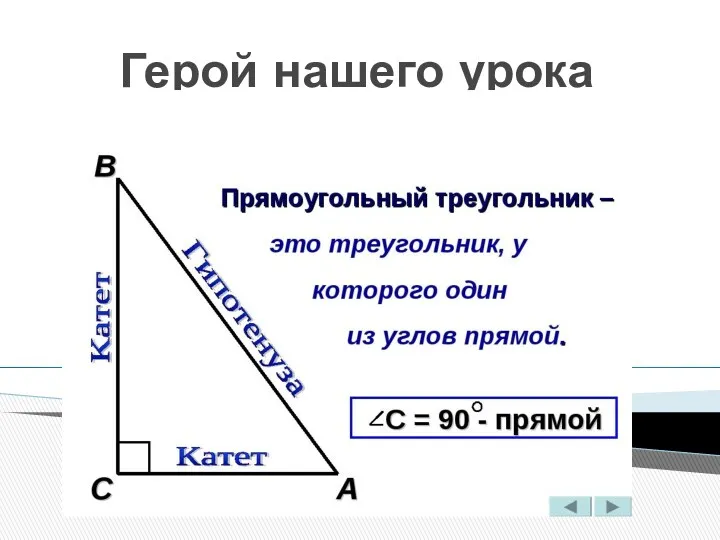 площадь прямоугольного треугольника
площадь прямоугольного треугольника Подобные слагаемые
Подобные слагаемые урок Тригонометрическая функция
урок Тригонометрическая функция Успешные люди открытый урок 10 класс алгебра и начала анализа
Успешные люди открытый урок 10 класс алгебра и начала анализа Итоговое повторение по теме Решение уравнений. 9 класс
Итоговое повторение по теме Решение уравнений. 9 класс оригинальное начало урока
оригинальное начало урока Компьютерная презентация к занятиям по теме Кривые второго порядка на плоскости для студентов 2 курса СПО
Компьютерная презентация к занятиям по теме Кривые второго порядка на плоскости для студентов 2 курса СПО Презентация математической игры Брейн - ринг для 8 класса.
Презентация математической игры Брейн - ринг для 8 класса. Технология развития критического мышления
Технология развития критического мышления