Содержание
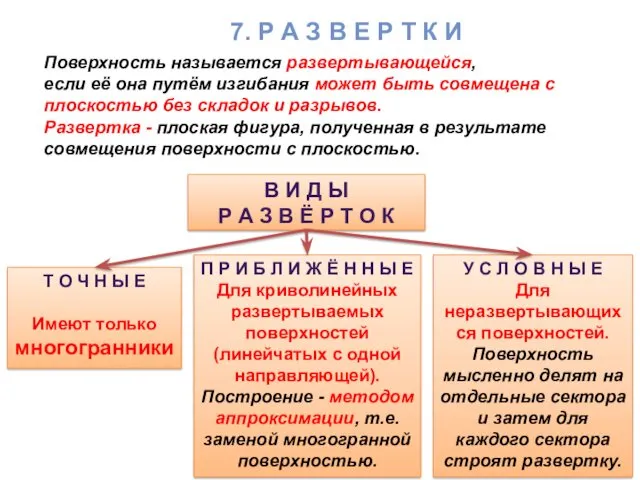
- 2. 7. Р А З В Е Р Т К И Поверхность называется развертывающейся, если её она
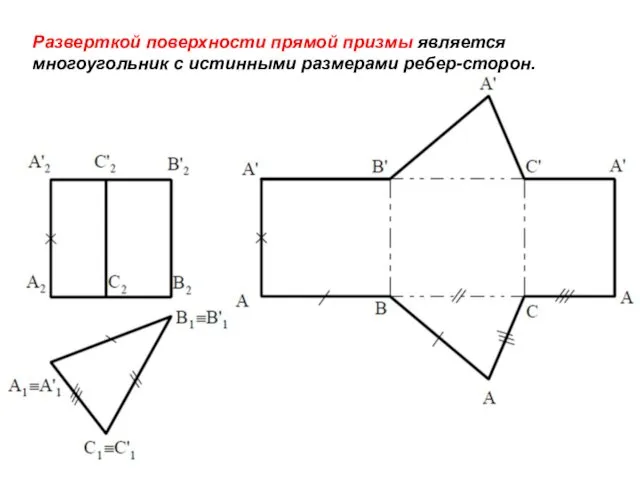
- 4. Разверткой поверхности прямой призмы является многоугольник с истинными размерами ребер-сторон.
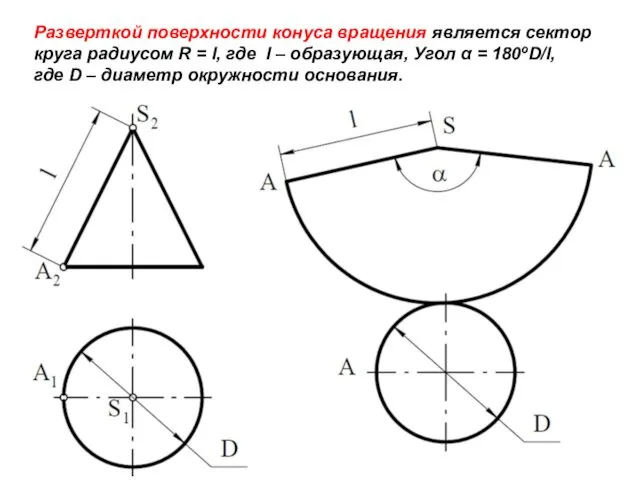
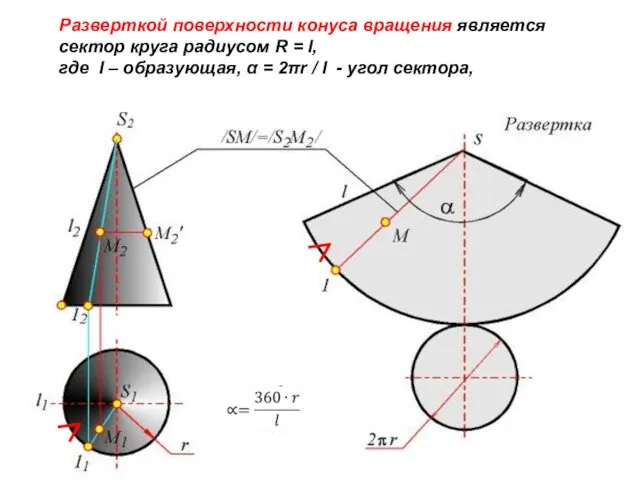
- 5. Разверткой поверхности конуса вращения является сектор круга радиусом R = l, где l – образующая, Угол
- 6. Разверткой поверхности конуса вращения является сектор круга радиусом R = l, где l – образующая, α
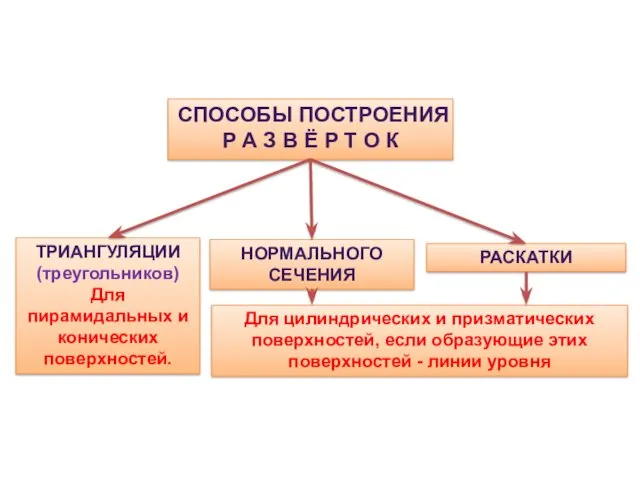
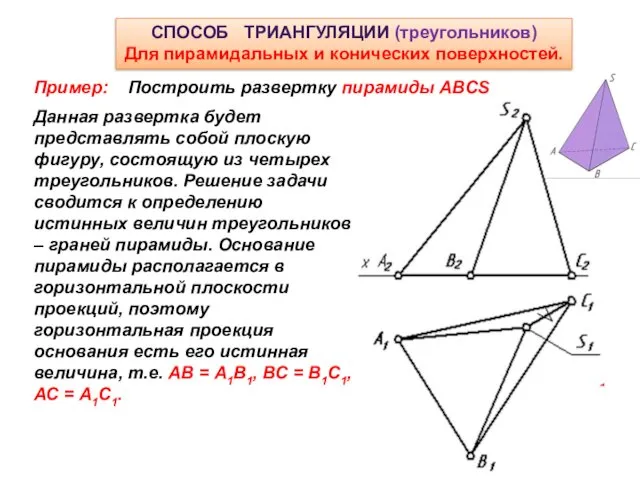
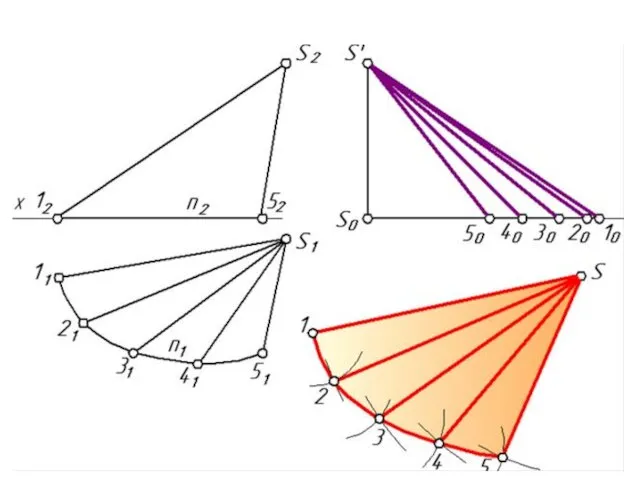
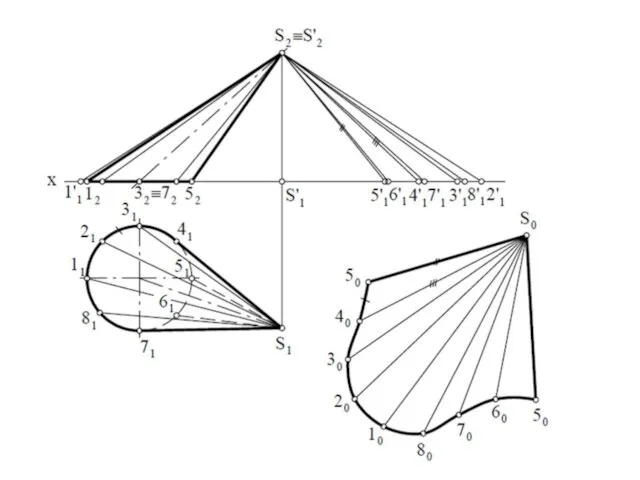
- 7. СПОСОБ ТРИАНГУЛЯЦИИ (треугольников) Для пирамидальных и конических поверхностей. Пример: Построить развертку пирамиды ABCS Данная развертка будет
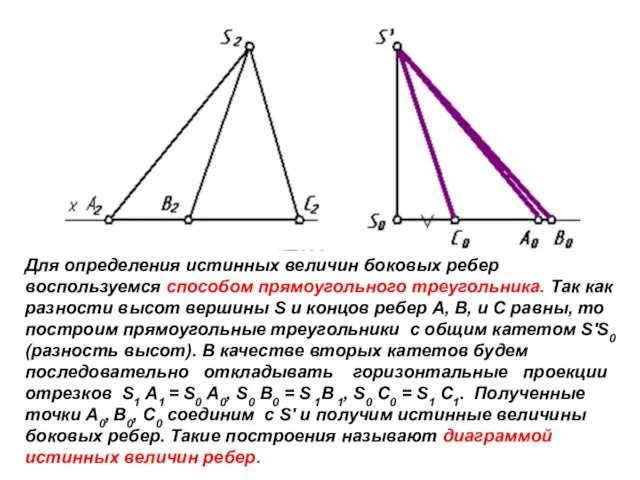
- 8. Для определения истинных величин боковых ребер воспользуемся способом прямоугольного треугольника. Так как разности высот вершины S
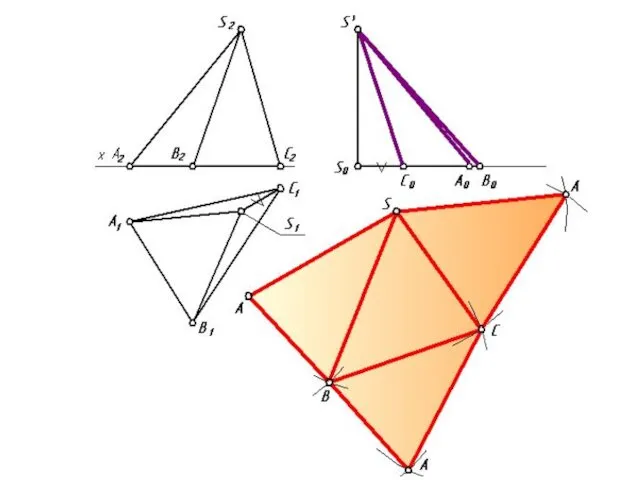
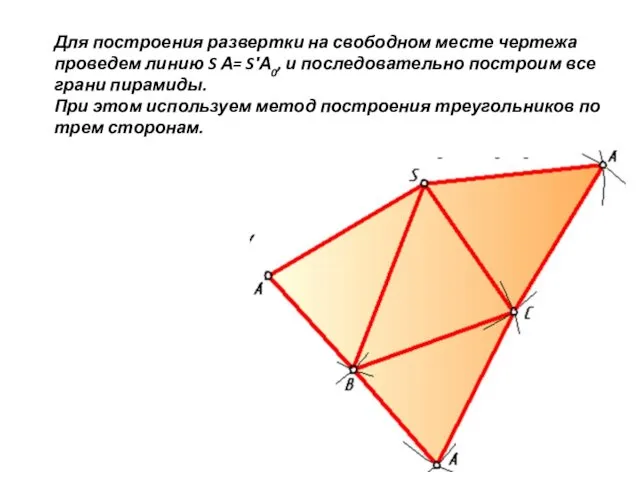
- 10. Для построения развертки на свободном месте чертежа проведем линию S А= S′А0, и последовательно построим все
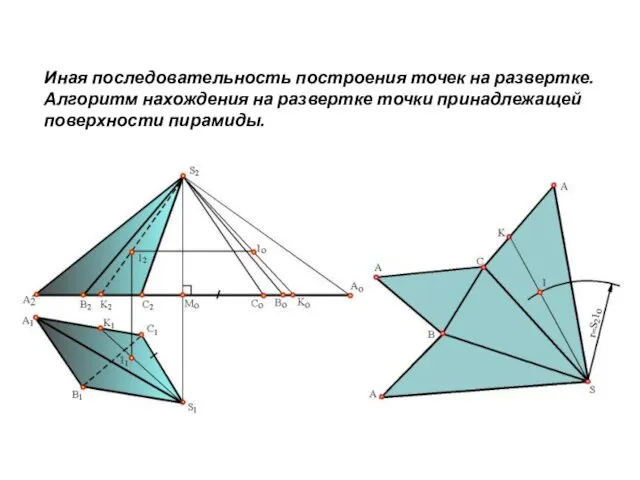
- 11. Иная последовательность построения точек на развертке. Алгоритм нахождения на развертке точки принадлежащей поверхности пирамиды.
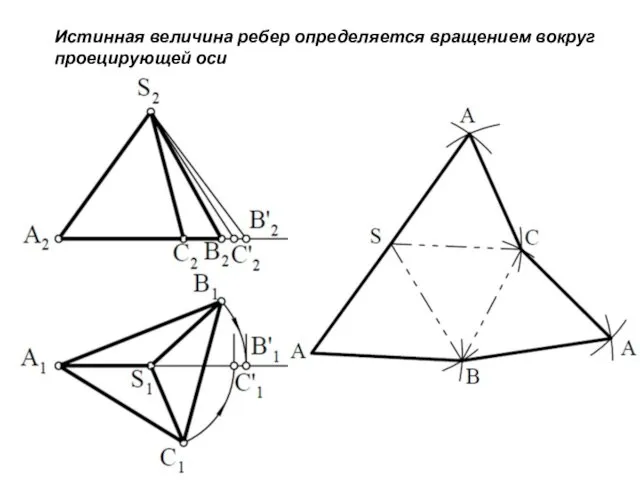
- 12. Истинная величина ребер определяется вращением вокруг проецирующей оси
- 13. Для построения развертки конической поверхности применяем метод аппроксимации, т. е. вписываем в эту поверхность или описываем
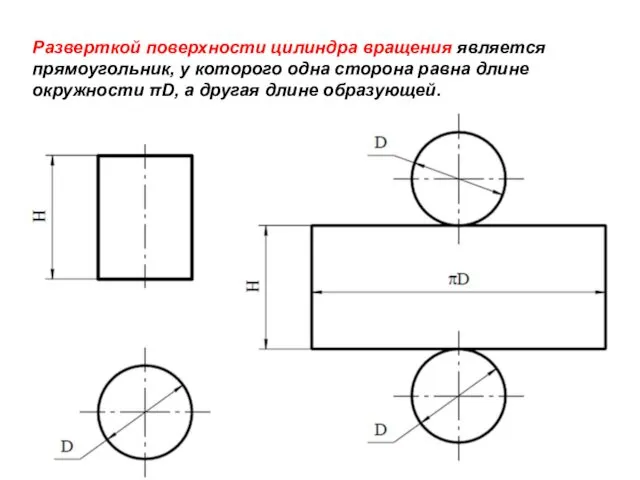
- 16. Разверткой поверхности цилиндра вращения является прямоугольник, у которого одна сторона равна длине окружности πD, а другая
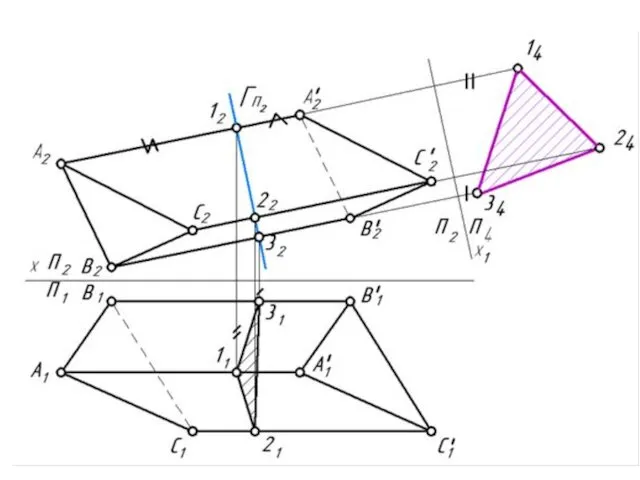
- 17. СПОСОБ НОРМАЛЬНОГО СЕЧЕНИЯ Для цилиндрических и призматических поверхностей, если образующие этих поверхностей - линии уровня Сущность
- 20. На свободном поле чертежа проводим горизонтальную прямую и последовательно откладываем на ней отрезки 12=14 24, 23=24
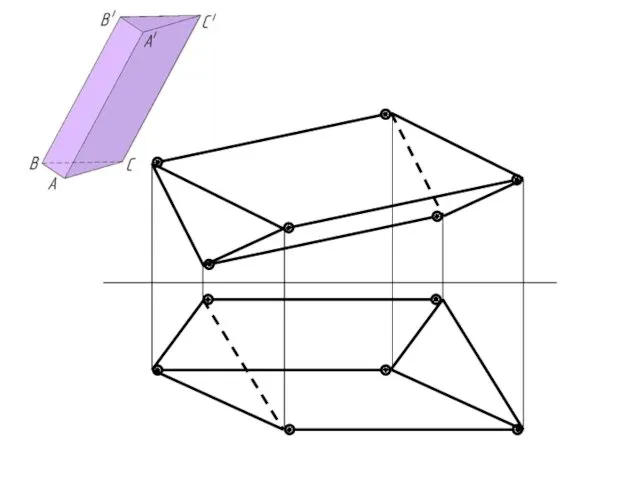
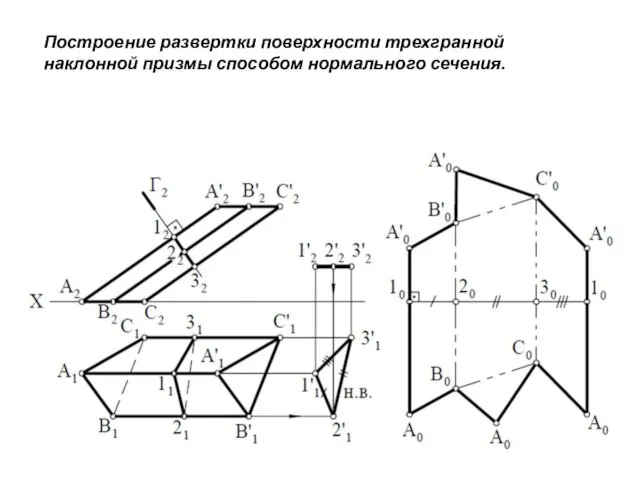
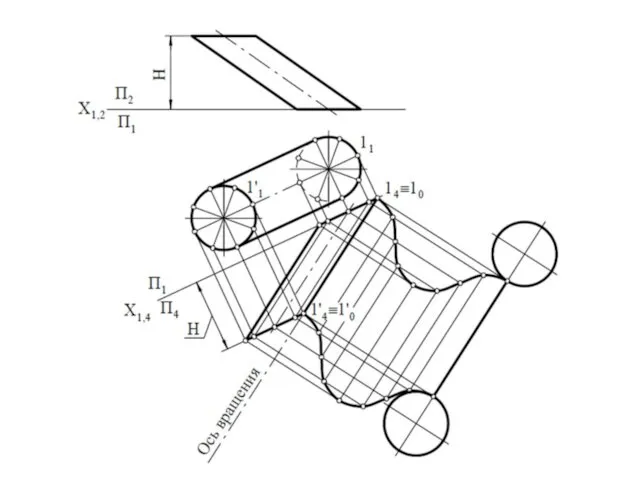
- 21. Построение развертки поверхности трехгранной наклонной призмы способом нормального сечения.
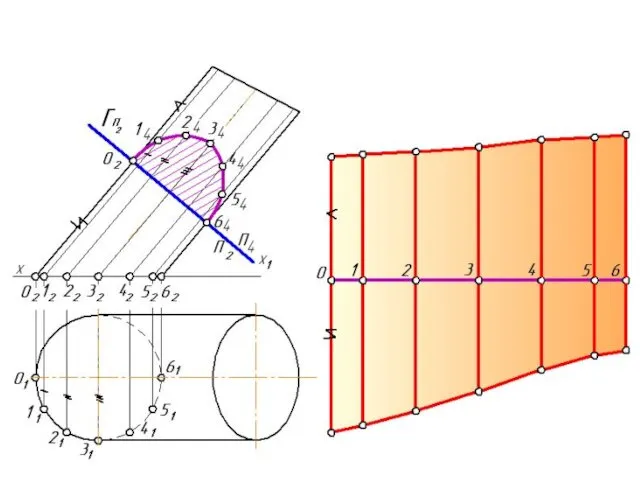
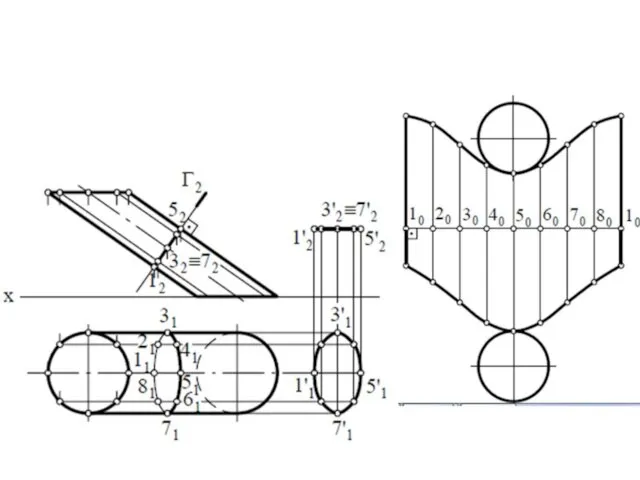
- 22. Пример: Построить развертку цилиндрической поверхности Применяя метод аппроксимации, заменим цилиндрическую поверхность призматической. Так как поверхность симметрична
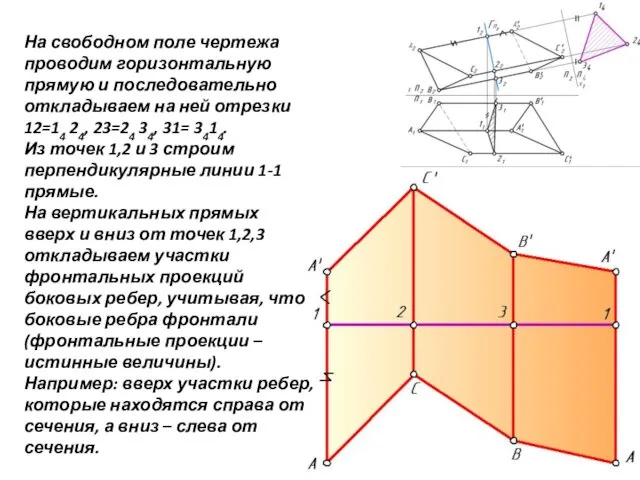
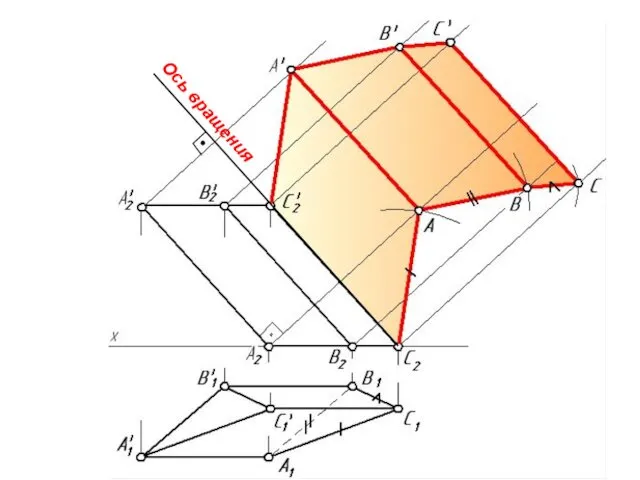
- 25. СПОСОБ РАСКАТКИ Способ раскатки применяется для построения разверток цилиндрических и призматических поверхностей, если образующими и направляющими
- 26. Для этого строим лучи из точек А2, В2, С2 перпендикулярно фронтальным проекциям А2А2', В2В2' и С2С2'.
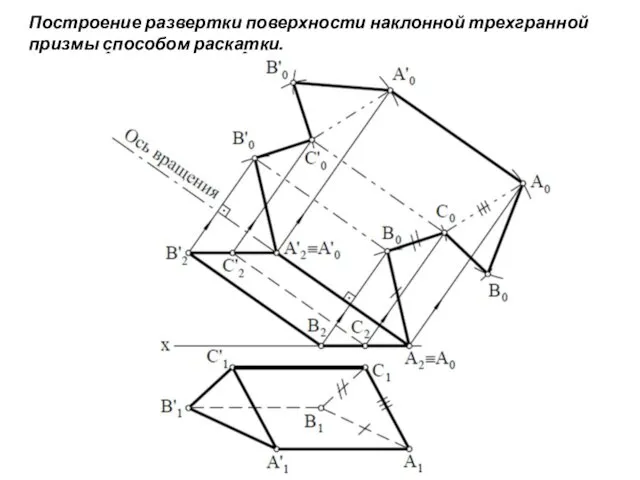
- 28. Построение развертки поверхности наклонной трехгранной призмы способом раскатки.
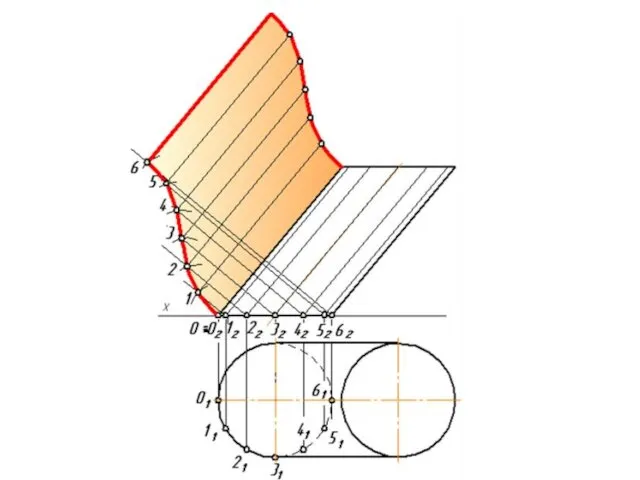
- 29. Пример: Построить развертку цилиндрической поверхности. Образующие поверхности - фронтали, а направляющая лежит в горизонтальной плоскости проекций.
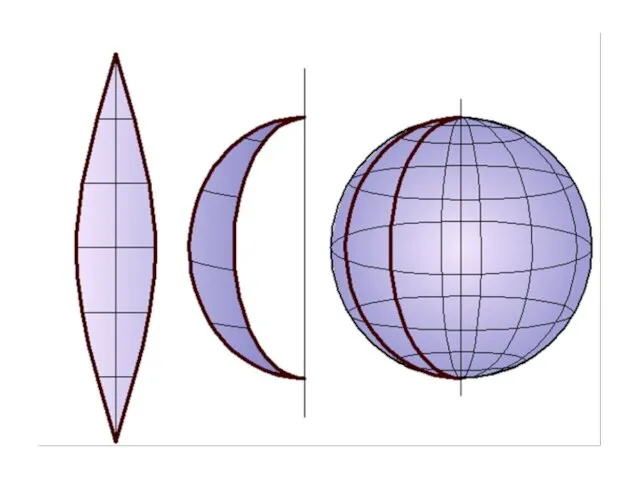
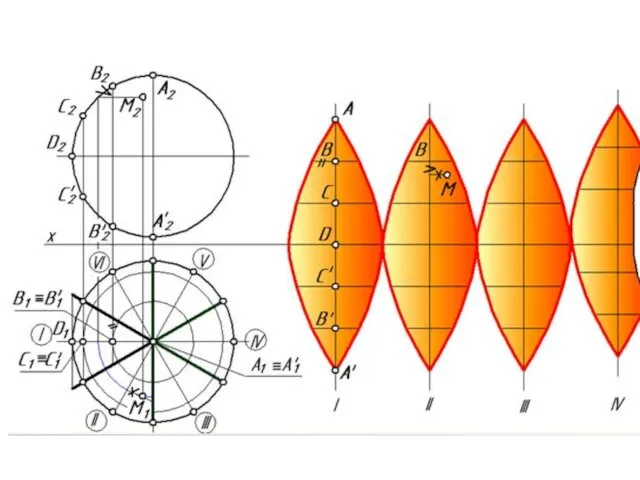
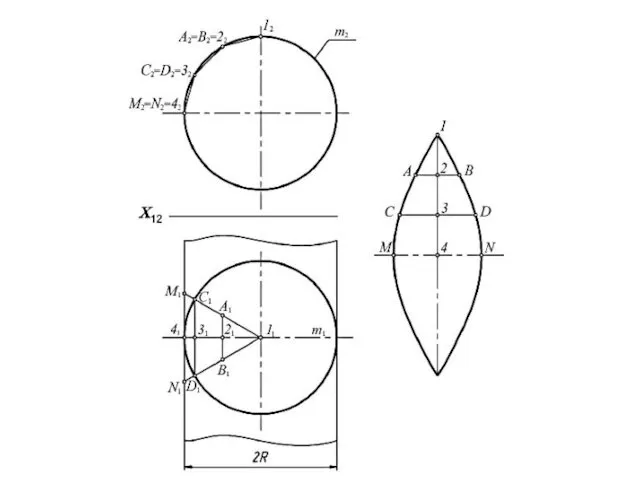
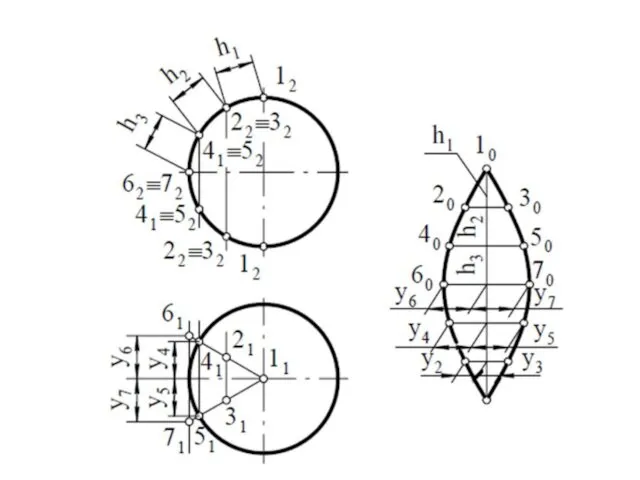
- 32. Условные развертки Строятся для не развертывающихся поверхностей. Сущность этого метода заключается в том, что поверхность мысленно
- 33. Через полученные точки А, А', В, В', С, С' и D проведем горизонтальные прямые и вправо
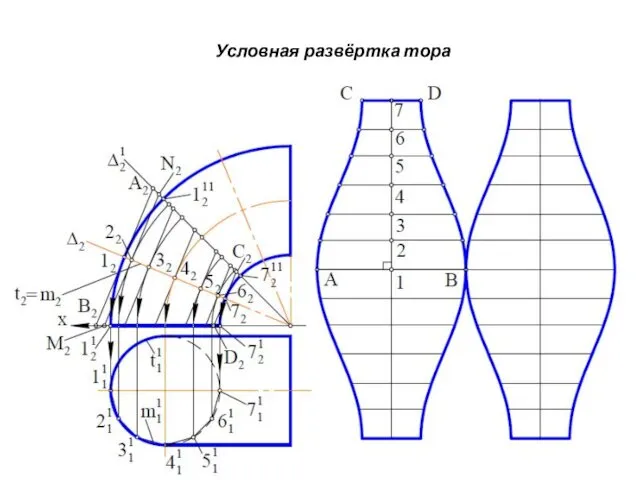
- 38. Условная развёртка тора
- 40. Скачать презентацию








 Статически определимые плоские фермы
Статически определимые плоские фермы Изображения - виды, разрезы, сечения
Изображения - виды, разрезы, сечения Геометрические построения
Геометрические построения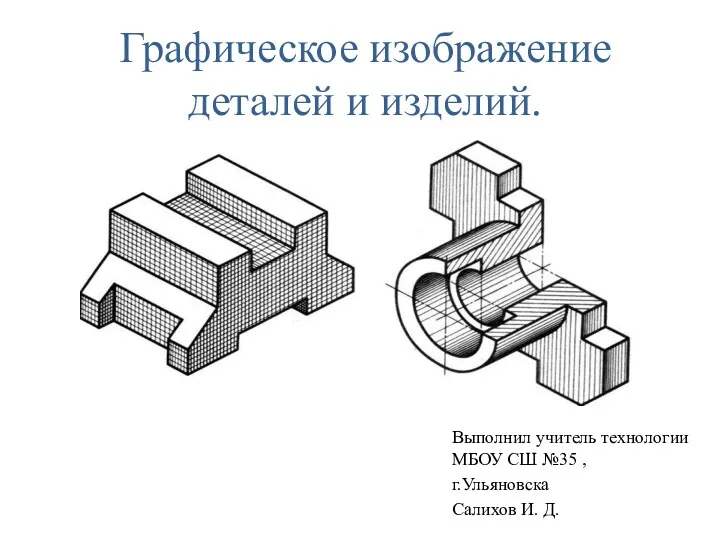 Графическое изображение детали
Графическое изображение детали Функциональные схемы гостиничных комплексов. Типология
Функциональные схемы гостиничных комплексов. Типология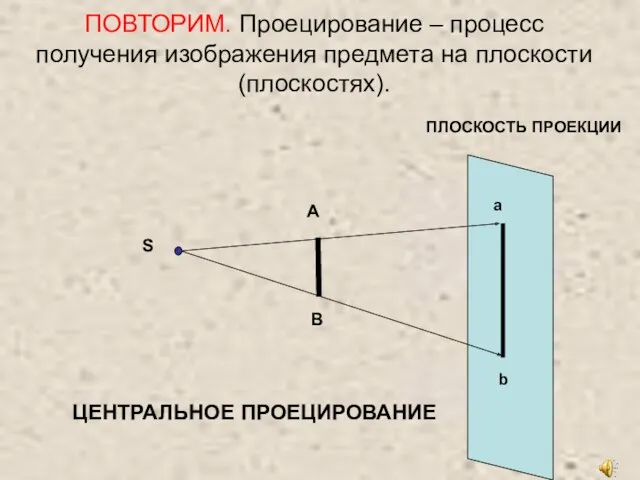 Проецирование – процесс получения изображения предмета на плоскости (плоскостях). 8 класс
Проецирование – процесс получения изображения предмета на плоскости (плоскостях). 8 класс Начертательная геометрия
Начертательная геометрия Чертеж общего вида и сборочный чертеж
Чертеж общего вида и сборочный чертеж Нанесение размеров. Масштаб
Нанесение размеров. Масштаб Чертежный шрифт
Чертежный шрифт Виды, разрезы, сечения. ГОСТ 2.305-2008
Виды, разрезы, сечения. ГОСТ 2.305-2008 Аксонометрические проекции окружностей. 8 класс
Аксонометрические проекции окружностей. 8 класс Офисные здания
Офисные здания Чертёжные инструменты, приборы, материалы и принадлежности
Чертёжные инструменты, приборы, материалы и принадлежности Общие сведения об изделиях и конструкторских документах
Общие сведения об изделиях и конструкторских документах Изображение и обозначение резьбы деталей
Изображение и обозначение резьбы деталей Графическая (конструкторская) документация
Графическая (конструкторская) документация Presentation of mud system - layout, appearance, winterization, equipment, environmental waste
Presentation of mud system - layout, appearance, winterization, equipment, environmental waste Строительное черчение
Строительное черчение Desen tehnic. Dispunerea proiectiilor
Desen tehnic. Dispunerea proiectiilor Анализ геометрической формы
Анализ геометрической формы Операционализация исследования
Операционализация исследования Нанесение размеров. Краткие сведения из ГОСТ 2.307-68. (Лекция 2)
Нанесение размеров. Краткие сведения из ГОСТ 2.307-68. (Лекция 2) Контрольная работа по разделу Техническое черчение
Контрольная работа по разделу Техническое черчение Построение теней в перспективе. Метод обратного луча. Метод лучевых сечений
Построение теней в перспективе. Метод обратного луча. Метод лучевых сечений Деталирование
Деталирование Шрифты
Шрифты Основные положения ЕСКД
Основные положения ЕСКД