Содержание
- 2. Метрическими называются такие задачи, в условии или решении которых присутствуют геометрические фигуры или понятия, связанные с
- 3. Метрические задачи связаны с различными измерениями: натуральных величин отрезков, углов, плоских фигур; расстояний между фигурами и
- 4. Из всего многообразия метрических задач выделяются две основные: 1. Первая основная метрическая задача - на перпендикулярность
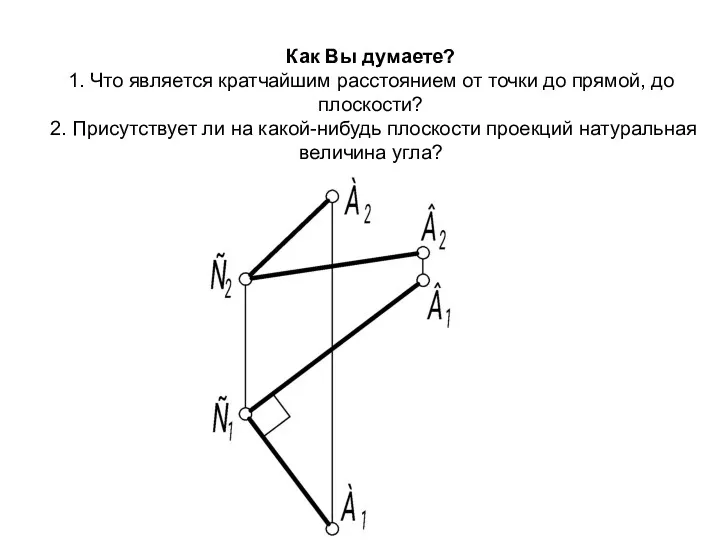
- 5. Как Вы думаете? 1. Что является кратчайшим расстоянием от точки до прямой, до плоскости? 2. Присутствует
- 6. Взаимная перпендикулярность прямой и плоскости. Из элементарной геометрии известно, что прямая перпендикулярна плоскости, если она перпендикулярна
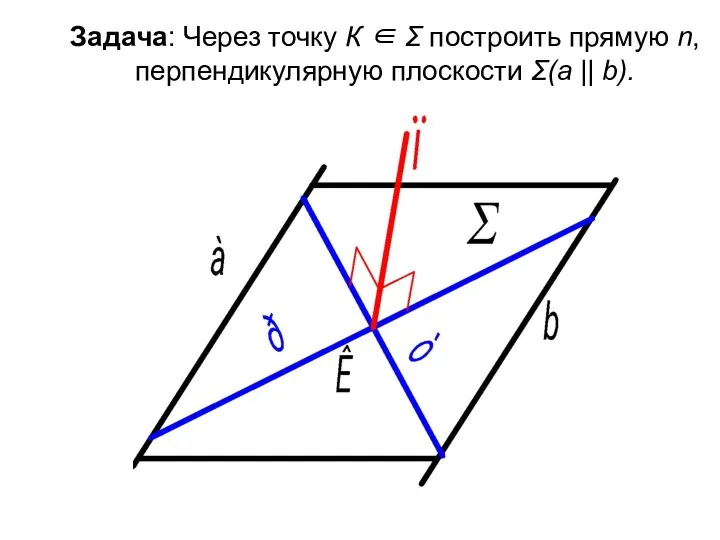
- 7. Задача: Через точку К ∈ Σ построить прямую n, перпендикулярную плоскости Σ(а || b).
- 8. Чтобы провести прямую n ⊥ Σ, нужно в этой плоскости взять две пересекающиеся прямые, это р
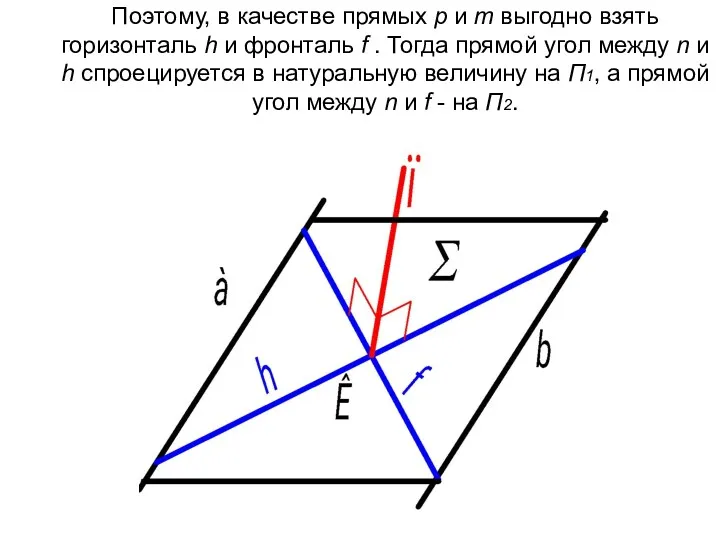
- 9. Поэтому, в качестве прямых р и m выгодно взять горизонталь h и фронталь f . Тогда
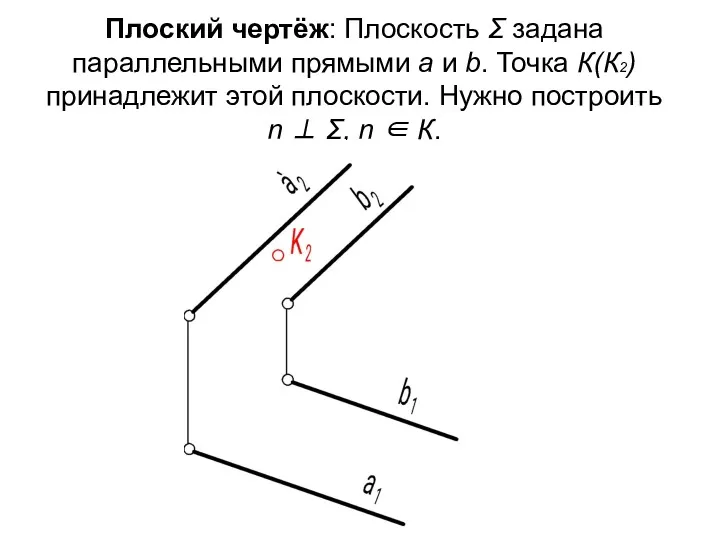
- 10. Плоский чертёж: Плоскость Σ задана параллельными прямыми а и b. Точка К(К2) принадлежит этой плоскости. Нужно
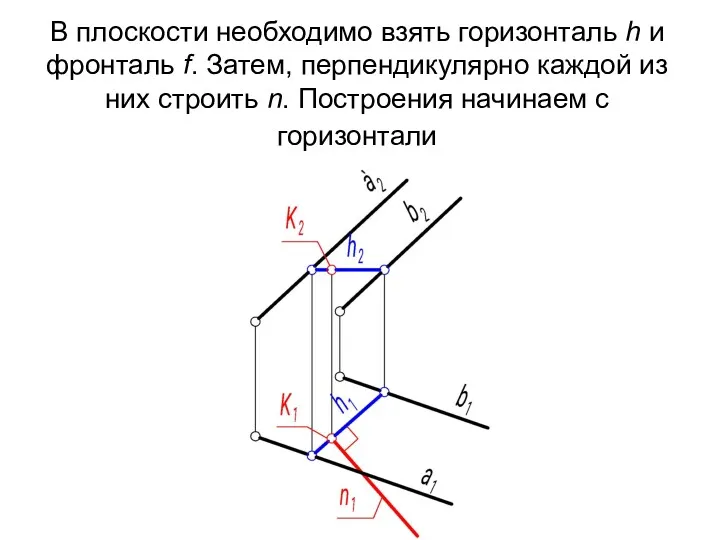
- 11. В плоскости необходимо взять горизонталь h и фронталь f. Затем, перпендикулярно каждой из них строить n.
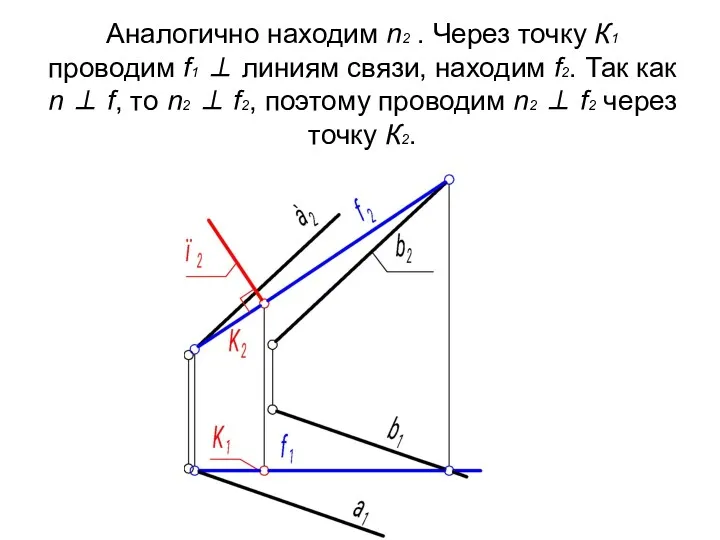
- 12. Аналогично находим n2 . Через точку К1 проводим f1 ⊥ линиям связи, находим f2. Так как
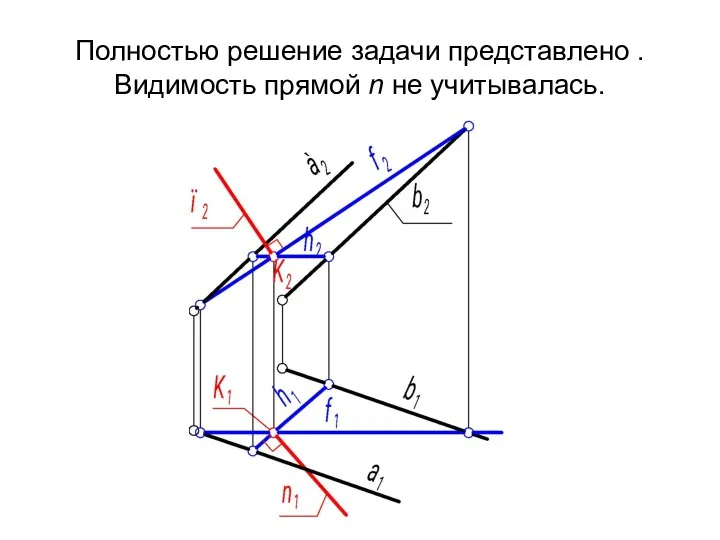
- 13. Полностью решение задачи представлено . Видимость прямой n не учитывалась.
- 14. Алгоритмическая запись решения: 1. h ⊂ Σ, f ⊂ Σ, h ∩ f = K. 2.
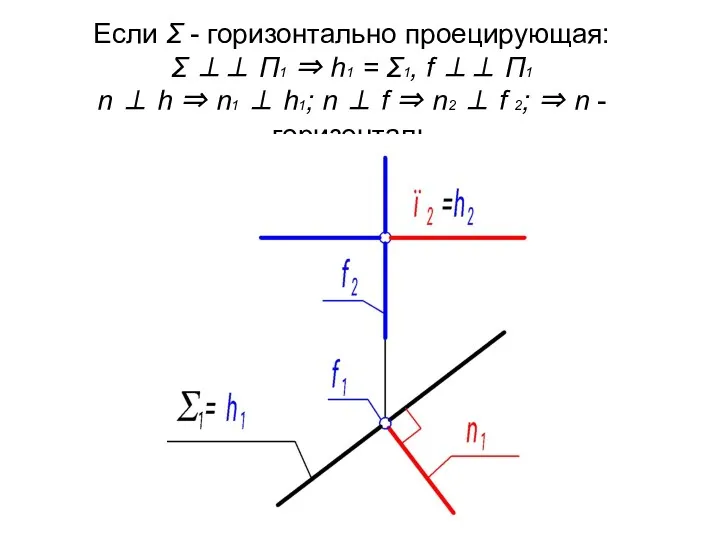
- 15. Если Σ - горизонтально проецирующая: Σ ⊥⊥ П1 ⇒ h1 = Σ1, f ⊥⊥ П1 n
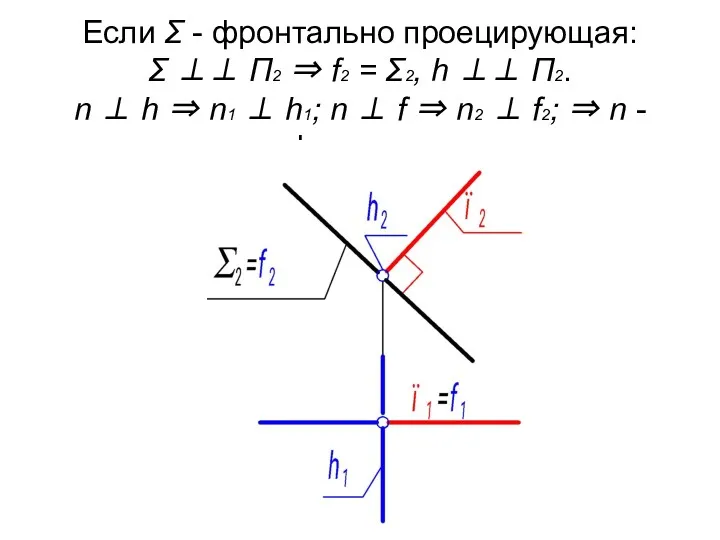
- 16. Если Σ - фронтально проецирующая: Σ ⊥⊥ П2 ⇒ f2 = Σ2, h ⊥⊥ П2. n
- 17. Если плоскость Σ занимает проецирующее положение, то прямая, перпендикулярная ей, является линией уровня(фронталь, горизонталь). Чтобы лучше
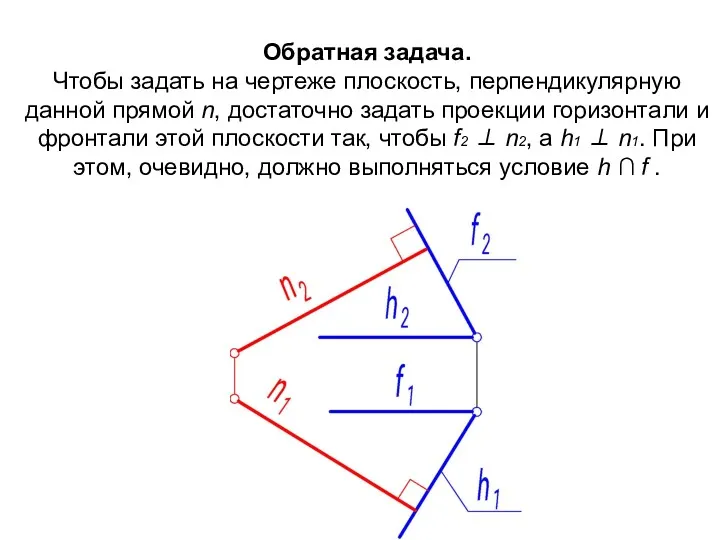
- 18. Обратная задача. Чтобы задать на чертеже плоскость, перпендикулярную данной прямой n, достаточно задать проекции горизонтали и
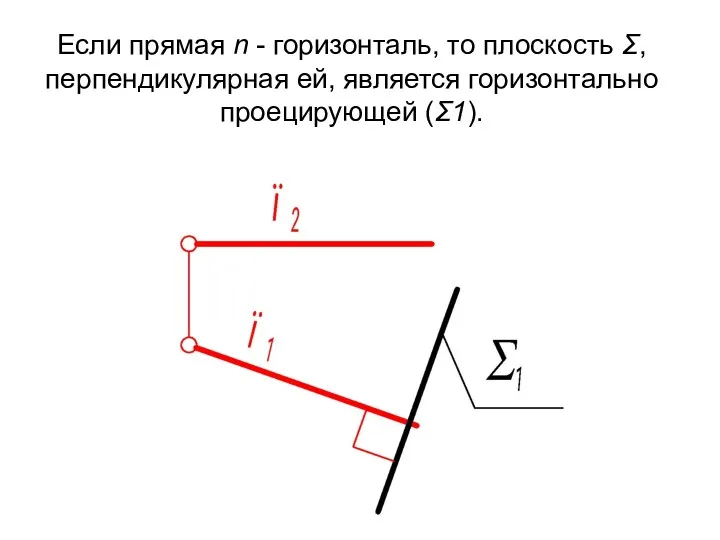
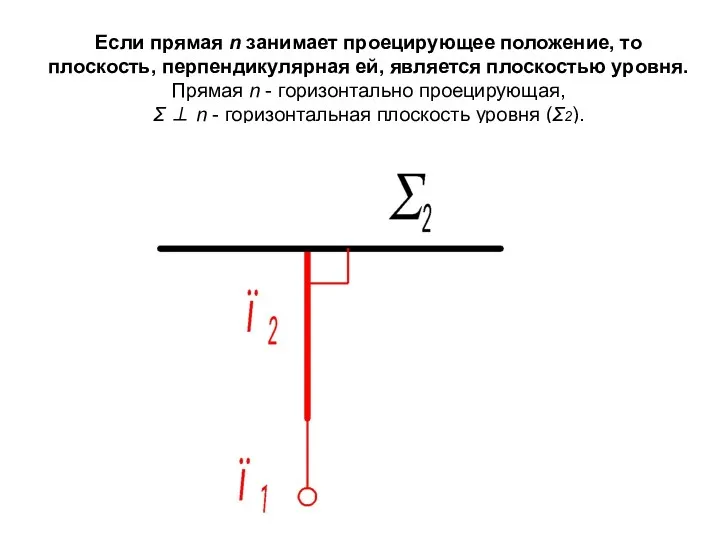
- 19. Если прямая n - горизонталь, то плоскость Σ, перпендикулярная ей, является горизонтально проецирующей (Σ1).
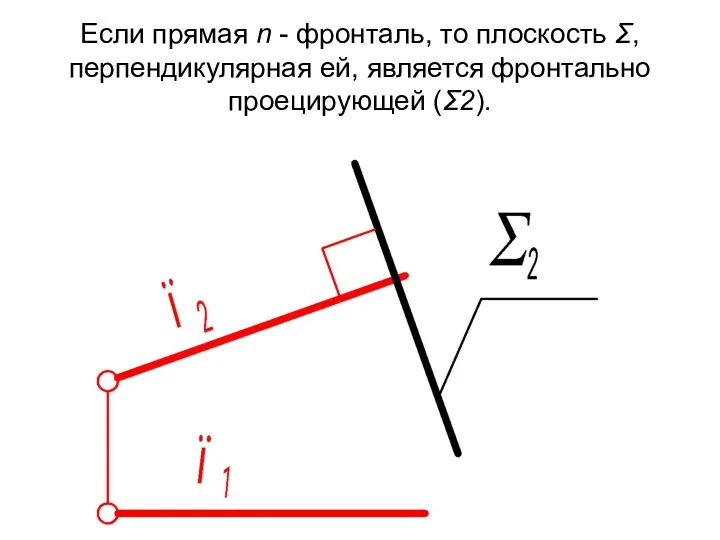
- 20. Если прямая n - фронталь, то плоскость Σ, перпендикулярная ей, является фронтально проецирующей (Σ2).
- 21. Если прямая n занимает проецирующее положение, то плоскость, перпендикулярная ей, является плоскостью уровня. Прямая n -
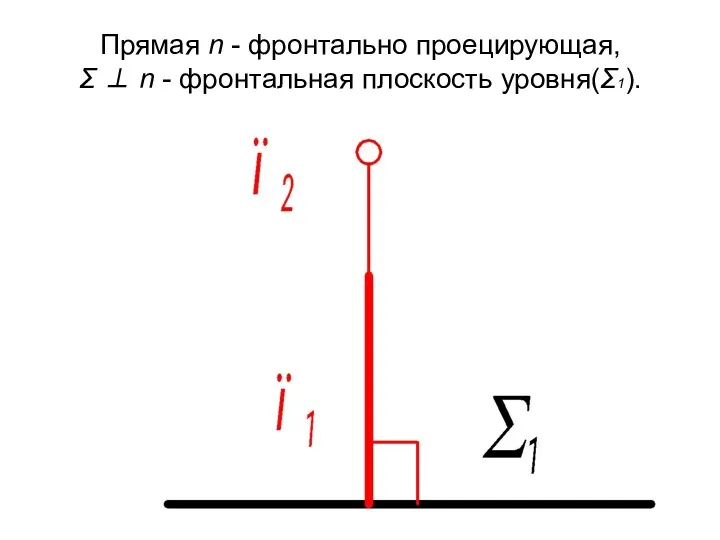
- 22. Прямая n - фронтально проецирующая, Σ ⊥ n - фронтальная плоскость уровня(Σ1).
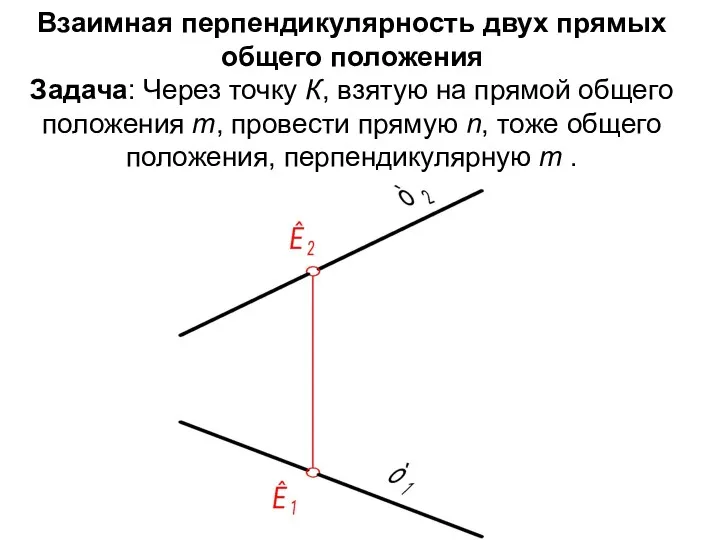
- 23. Взаимная перпендикулярность двух прямых общего положения Задача: Через точку К, взятую на прямой общего положения m,
- 24. Так как прямой угол между прямыми общего положения искажается на обеих плоскостях проекций, то решение задачи
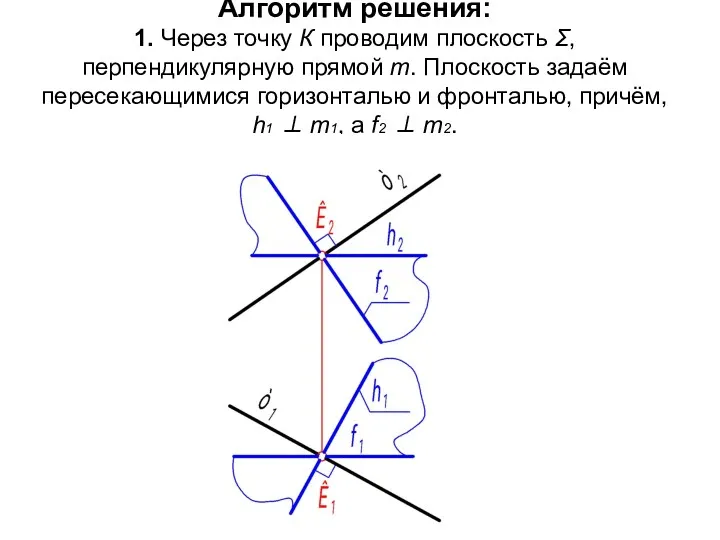
- 25. Алгоритм решения: 1. Через точку К проводим плоскость Σ, перпендикулярную прямой m. Плоскость задаём пересекающимися горизонталью
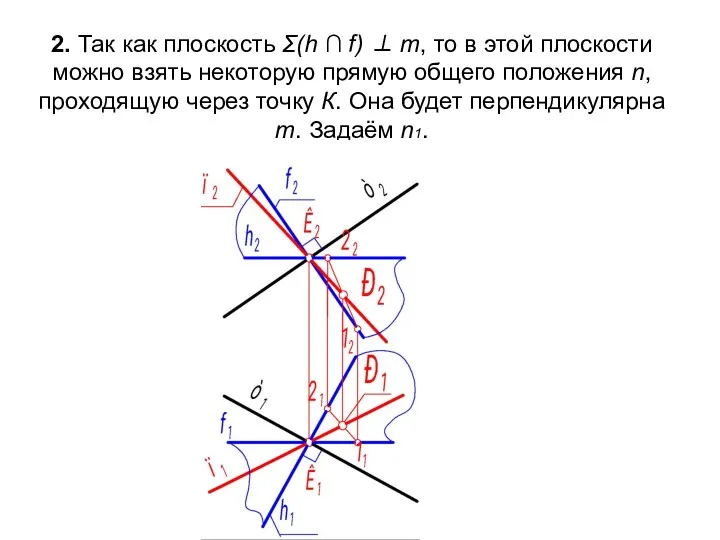
- 26. 2. Так как плоскость Σ(h ∩ f) ⊥ m, то в этой плоскости можно взять некоторую
- 27. 3. Известно, что прямую определяют две точки. На n1, кроме К1, возьмём ещё одну точку Р1.
- 28. Алгоритмическая запись решения: Σ ⊥ m, Σ = h ∩ f = K; h ⊥ m
- 29. Взаимная перпендикулярность двух плоскостей общего положения Известно, что две плоскости взаимно перпендикулярны, если в одной из
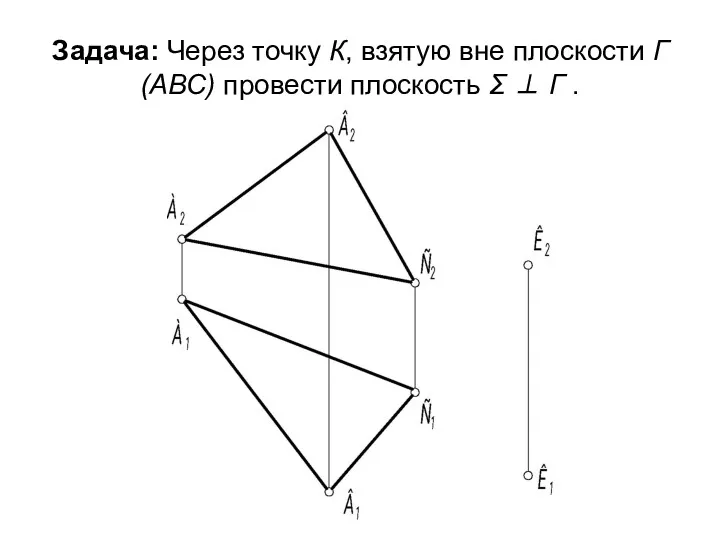
- 30. Задача: Через точку К, взятую вне плоскости Г(АВС) провести плоскость Σ ⊥ Г .
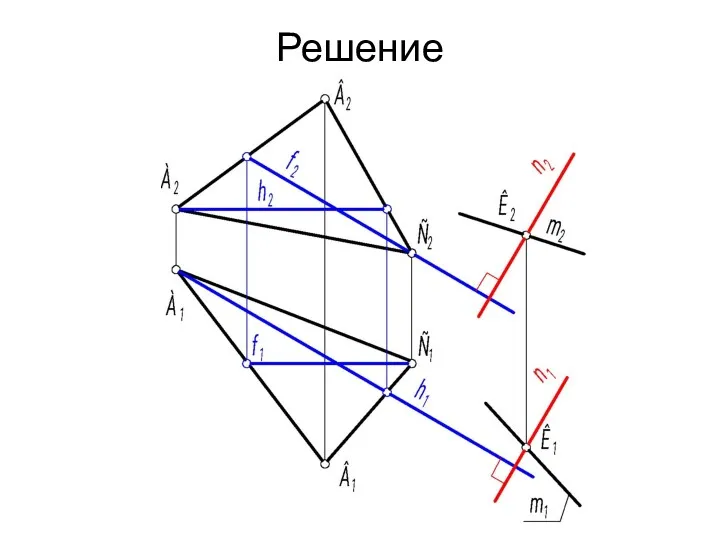
- 31. Алгоритм: 1. Плоскость Σ задаём пересекающимися прямыми m ∩ n = К. Согласно вышесказанному, одна из
- 32. Решение
- 33. Алгоритмическая запись решения: 1. h ⊂ Г ⇒ h2 ⇒ h1, f ⊂ Г ⇒ f1
- 34. Построение плоскости, касательной к поверхности Касательная плоскость - это множество всех касательных прямых, проведённых к данной
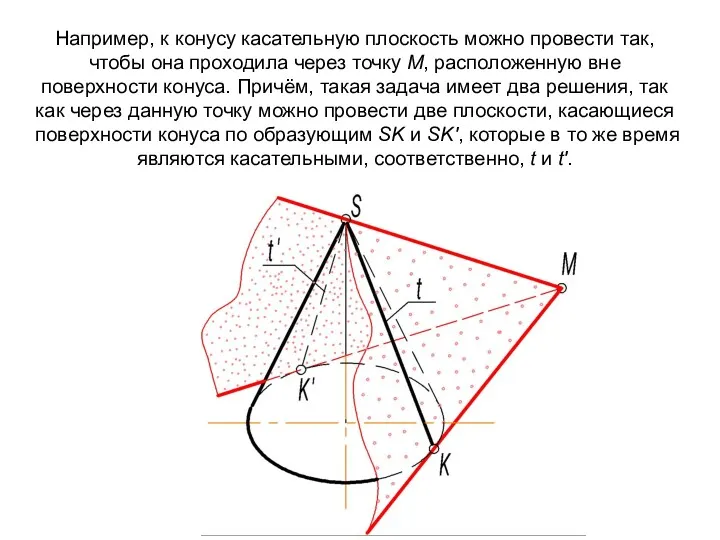
- 35. Например, к конусу касательную плоскость можно провести так, чтобы она проходила через точку М, расположенную вне
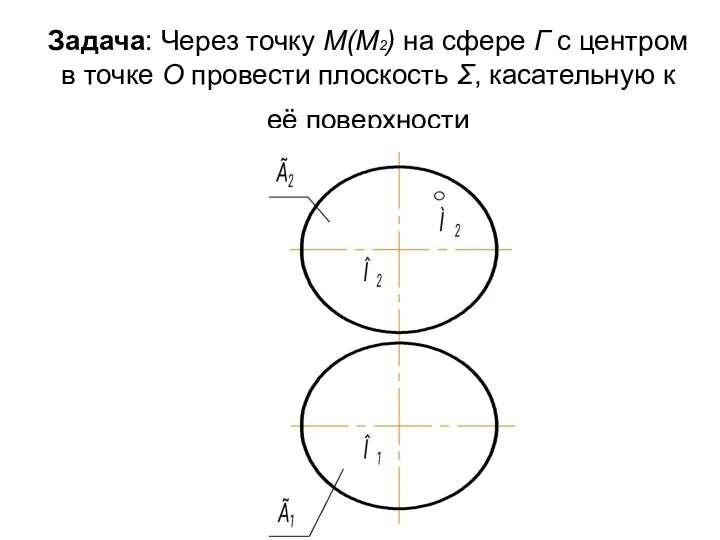
- 36. Задача: Через точку М(М2) на сфере Г с центром в точке О провести плоскость Σ, касательную
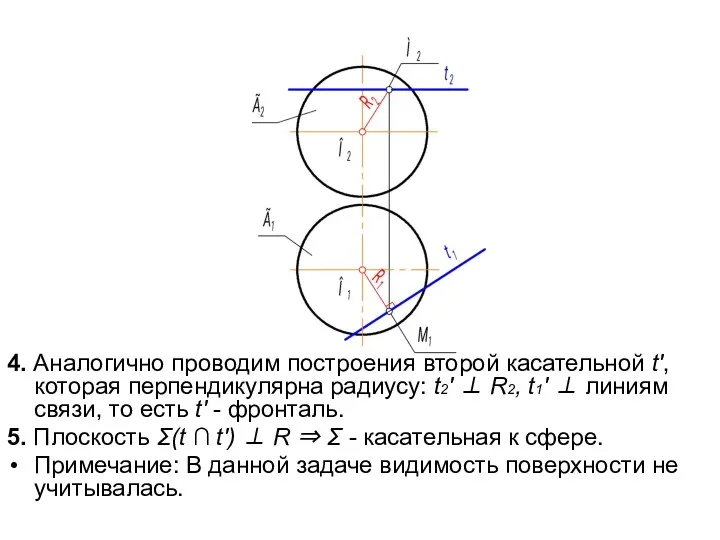
- 37. Так как любая прямая, принадлежащая касательной плоскости к сфере, будет перпендикулярна к её радиусу, то задача
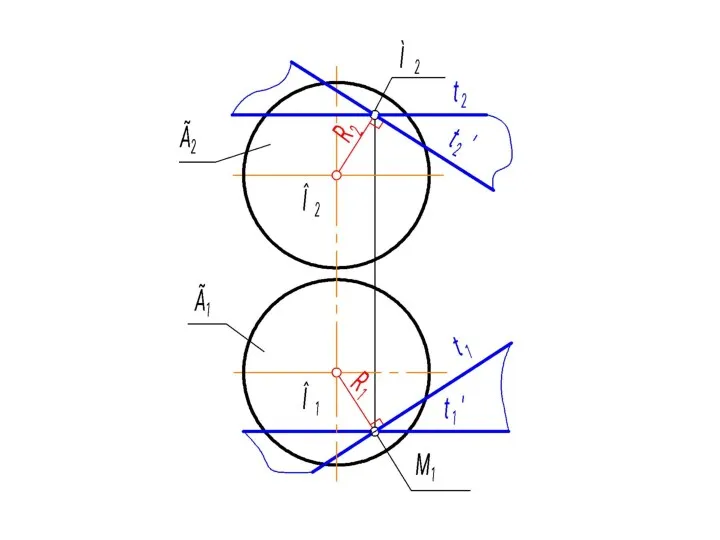
- 38. 4. Аналогично проводим построения второй касательной t', которая перпендикулярна радиусу: t2' ⊥ R2, t1' ⊥ линиям
- 40. Алгоритмическая запись решения: 1. М ∈ Г ⇒ М1. 2. ОМ = R ⇒ O1M1 =
- 41. Задачи на определение расстояний между геометрическими фигурами К таким задачам относятся: задачи на определение расстояний от
- 42. Все эти задачи объединяют три обстоятельства: во-первых, поскольку кратчайшим расстоянием между такими фигурами является перпендикуляр, то
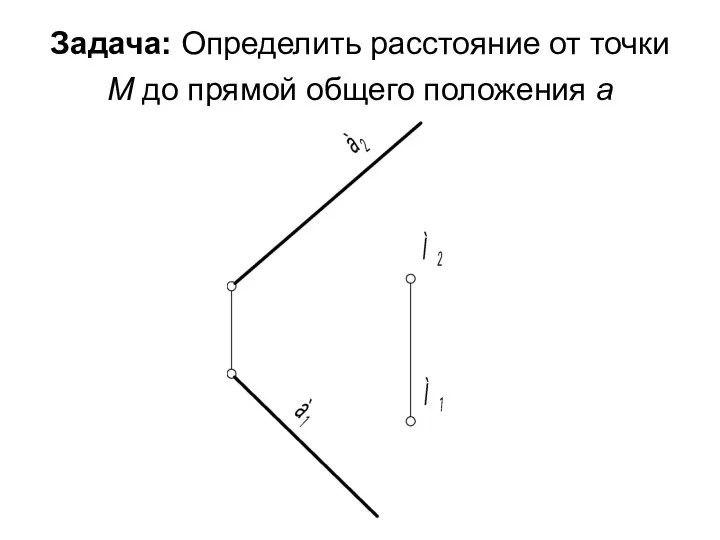
- 43. Задача: Определить расстояние от точки М до прямой общего положения а
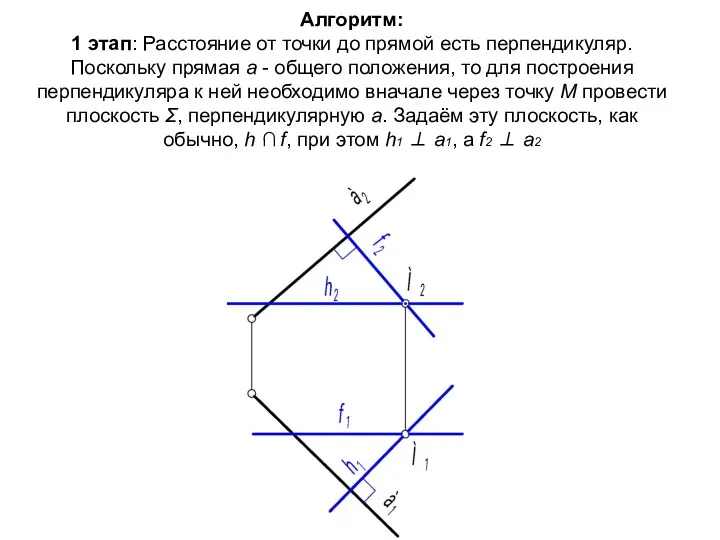
- 44. Алгоритм: 1 этап: Расстояние от точки до прямой есть перпендикуляр. Поскольку прямая а - общего положения,
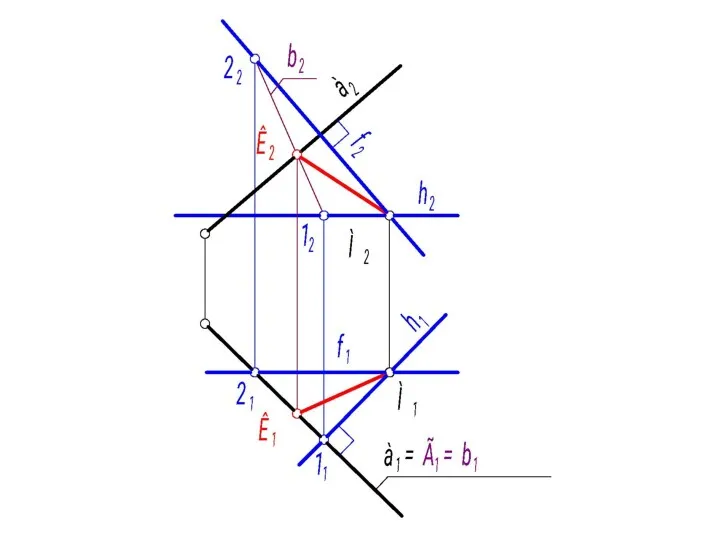
- 45. 2 этап: Для построения перпендикуляра необходимо найти для него вторую точку. Это будет точка К, принадлежащая
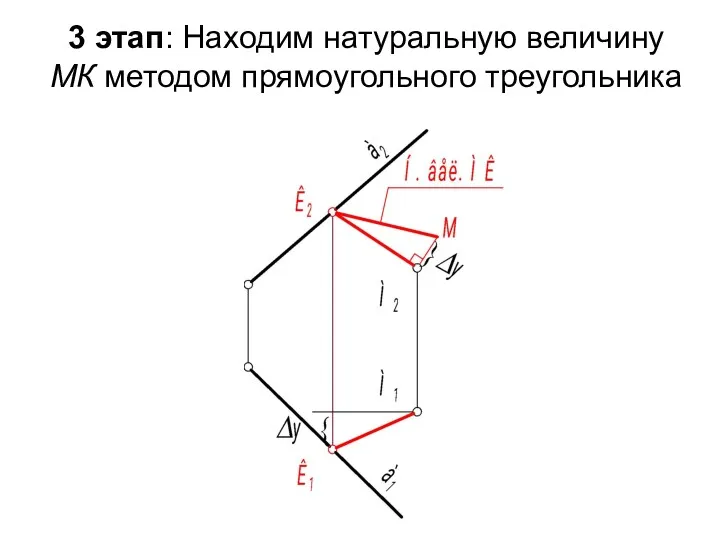
- 47. 3 этап: Находим натуральную величину МК методом прямоугольного треугольника
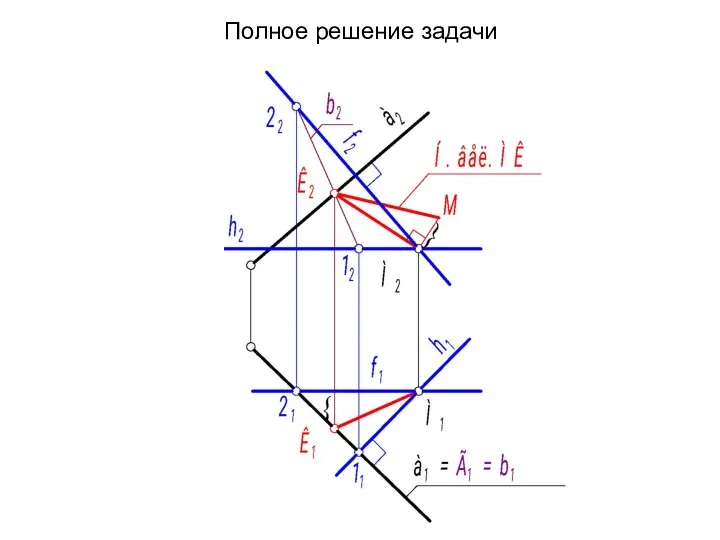
- 48. Полное решение задачи
- 49. Алгоритмическая запись решения: 1. Σ ⊥ а, Σ = h ∩ f = M, h1 ⊥
- 51. Скачать презентацию




















 Архитектурно-строительное черчение
Архитектурно-строительное черчение Фронтальная косоугольная диметрическая и прямоугольная изометрическая проекции
Фронтальная косоугольная диметрическая и прямоугольная изометрическая проекции Виды аксонометрии
Виды аксонометрии Соединения разъёмные
Соединения разъёмные Резьбовые соединения. Разъёмные соединения
Резьбовые соединения. Разъёмные соединения Метод проекций. Изображения виды, разрезы, сечения. Начертательная геометрия. Компьютерная графика. Лекция 1
Метод проекций. Изображения виды, разрезы, сечения. Начертательная геометрия. Компьютерная графика. Лекция 1 ЕСКД. Схемы. Виды и типы. Общие требования к выполнению
ЕСКД. Схемы. Виды и типы. Общие требования к выполнению Зображення об’єктів на технічних креслениках. Види. Лекція 2
Зображення об’єктів на технічних креслениках. Види. Лекція 2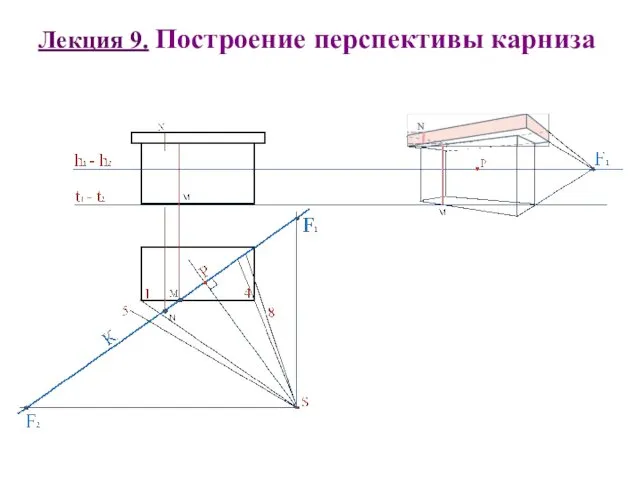 Построение перспективы карниза
Построение перспективы карниза Проецирование на одну плоскость проекций
Проецирование на одну плоскость проекций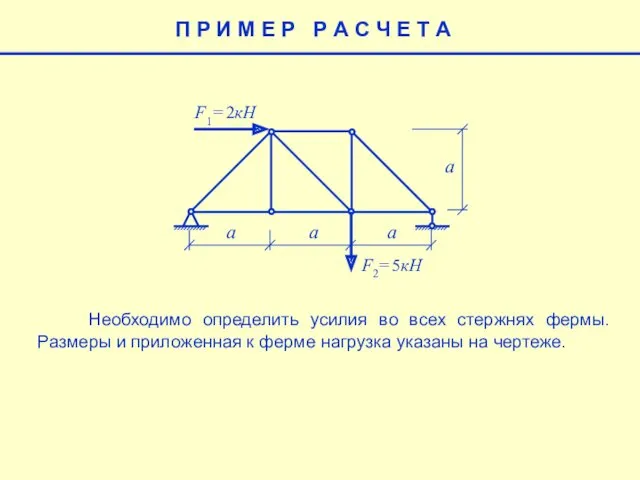 Определить усилия во всех стержнях фермы методом вырезания узлов
Определить усилия во всех стержнях фермы методом вырезания узлов Проецирование
Проецирование Инженерная графика. Введение
Инженерная графика. Введение Проецирование виды проецирования, проецирование на одну плоскость проекций
Проецирование виды проецирования, проецирование на одну плоскость проекций Правила нанесения размеров на чертежах
Правила нанесения размеров на чертежах Изображения – виды, разрезы, сечения
Изображения – виды, разрезы, сечения Следы прямой линии. Взаимное положение двух прямых. Тема №5
Следы прямой линии. Взаимное положение двух прямых. Тема №5 Соединения деталей. Резьбовые соединения. Лекция 3
Соединения деталей. Резьбовые соединения. Лекция 3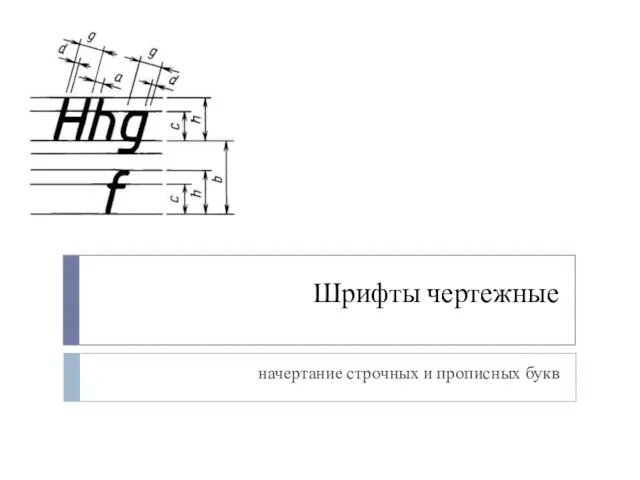 Шрифты чертежные. Начертание строчных и прописных букв
Шрифты чертежные. Начертание строчных и прописных букв Прямая линия. Способы задания прямой на эпюре
Прямая линия. Способы задания прямой на эпюре Проецирование прямой линии. Лекция 2
Проецирование прямой линии. Лекция 2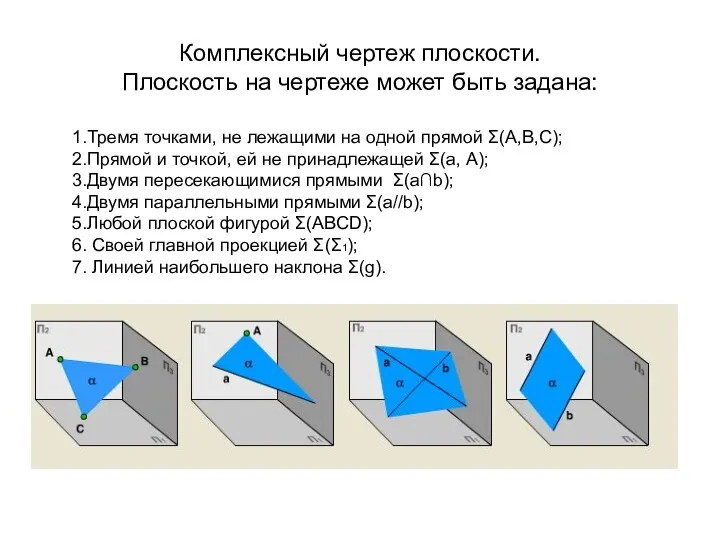 Комплексный чертеж плоскости. Плоскость на чертеже
Комплексный чертеж плоскости. Плоскость на чертеже Анализ геометрической формы предмета
Анализ геометрической формы предмета Руководство для выполнения графических работ
Руководство для выполнения графических работ Основи машинобудівного креслення. Класифікація видів, розрізів, перетинів
Основи машинобудівного креслення. Класифікація видів, розрізів, перетинів Основные задачи начертательной геометрии
Основные задачи начертательной геометрии Разрез здания
Разрез здания Правила вычерчивания и расчета монтажной схемы систем вентиляции
Правила вычерчивания и расчета монтажной схемы систем вентиляции