Содержание
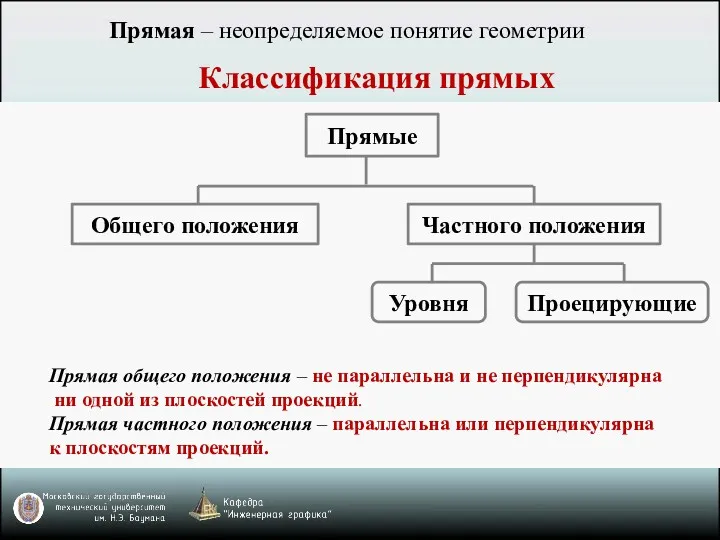
- 2. Классификация прямых Прямая общего положения – не параллельна и не перпендикулярна ни одной из плоскостей проекций.
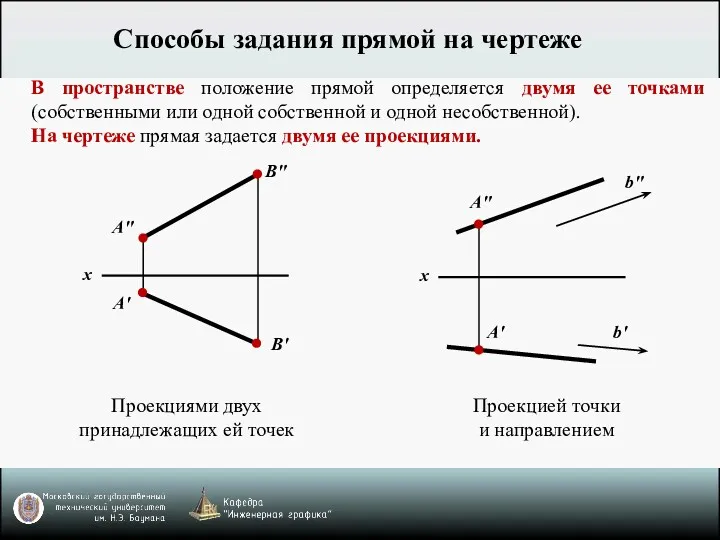
- 3. x А" А' В' В" x А" А' b" b' В пространстве положение прямой определяется двумя
- 4. π1 π2 x a A B A′ B′ A′′ B′′ а′ а′′ ≡ Ha' Ha'' ≡
- 5. ч Правило построения горизонтального (фронтального) следа прямой Продолжить фронтальную (горизонтальную) проекцию прямой a до пересечения с
- 6. x h'' B′ β zA Fh ≡ Fh'' Fh' A′′ A′ zB h′ Прямые частного положения.
- 7. A′ x B′ yA A′′ yB B′′ f ′ f ′′ α Hf ≡ Hf '
- 8. α A′′′ A′ x y y A′′ z B′′ B′′′ B′ p' p" p''' Fp ≡
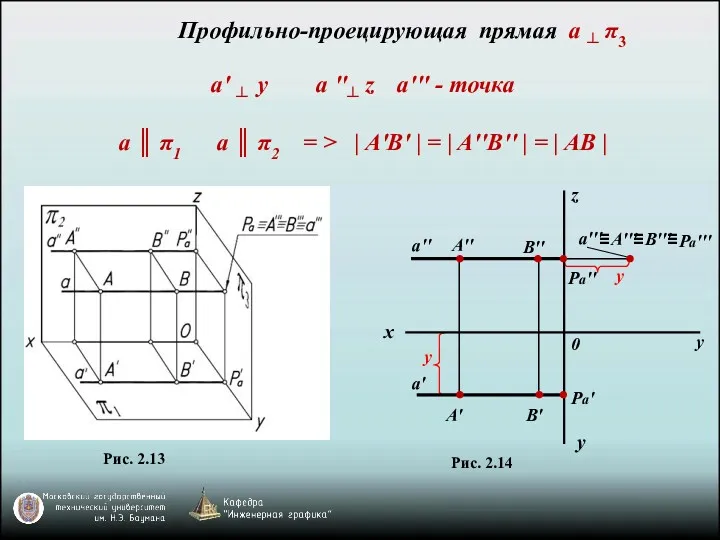
- 9. A′′ B′′ Ha'' a′′ Ha' A′ B′ x a′ ≡ ≡ Горизонтально-проецирующая прямая a ┴ π1
- 10. A′′ B′′ Fa' a′′ a′ A′ B′ x ≡ ≡ ≡ Fa'' Фронтально-проецирующая прямая a ┴
- 11. B′′ y y x z A′ B′ a′ A′′ a′′ Pa'' Pa''' Pa' A′′′ B′′′ a′′′
- 12. ОПРЕДЕЛЕНИЕ ДЛИНЫ ОТРЕЗКА ПРЯМОЙ ОБЩЕГО ПОЛОЖЕНИЯ И УГЛОВ НАКЛОНА ПРЯМОЙ К ПЛОСКСТЯМ ПРОЕКЦИЙ Отрезок прямой общего
- 13. A′ B′ B′′ A′′ ІABІ ІABІ A0 B0 ∆z ∆z Δy Δy β α Правило определения
- 14. Рис. 2.17 Алгоритм На прямой a выбирают произвольную точку C Определяют натуральную величину отрезка AC Откладывают
- 15. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ Рис. 2.18 Прямые пересекаются Прямые параллельны Пересечение прямых Если две прямые пересекаются в
- 16. Скрещивание прямых Скрещивающиеся прямые – не параллельны и не пересекаются, т. е. не лежат в одной
- 18. Скачать презентацию












 Резьбовые соединения
Резьбовые соединения Правила нанесения размеров на чертежах
Правила нанесения размеров на чертежах Сечения на чертеже
Сечения на чертеже Архитектура. Построение плана здания
Архитектура. Построение плана здания Портфолио. Архитектурная графика. Изображение архитектурного замысла при проектировании
Портфолио. Архитектурная графика. Изображение архитектурного замысла при проектировании Шрифт чертежный. Написание прописных и строчных букв
Шрифт чертежный. Написание прописных и строчных букв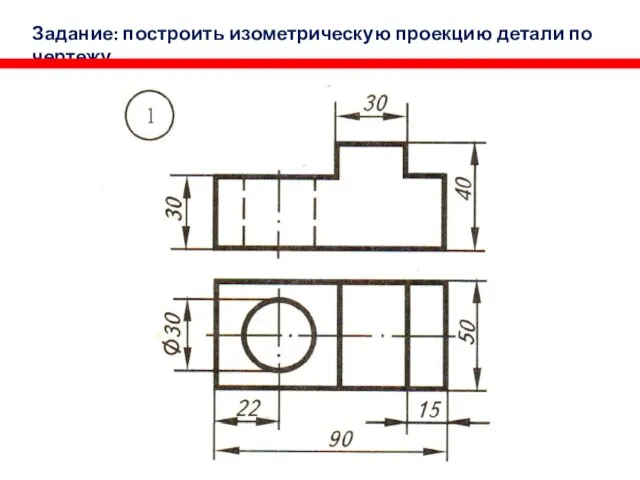 Задания (чертежи для построения изометрической проекции)
Задания (чертежи для построения изометрической проекции) Время. Смета проекта
Время. Смета проекта Чертежи деталей, изготовляемых на токарном и фрезерном станках
Чертежи деталей, изготовляемых на токарном и фрезерном станках Аксонометрические проекции
Аксонометрические проекции Сопряжения. Основные элементы сопряжения
Сопряжения. Основные элементы сопряжения Соединения деталей. Резьбовые соединения. Лекция 3
Соединения деталей. Резьбовые соединения. Лекция 3 Гранные и кривые поверхности. (Лекция 6)
Гранные и кривые поверхности. (Лекция 6) Правила выполнения структурных схем
Правила выполнения структурных схем Типы графических изображений: технический рисунок, эскиз, чертёж
Типы графических изображений: технический рисунок, эскиз, чертёж Проектування технологічного процесу виготовлення виливка Корпус з фланцем з мідного сплаву
Проектування технологічного процесу виготовлення виливка Корпус з фланцем з мідного сплаву Обозначение шероховатости поверхностей на чертежах
Обозначение шероховатости поверхностей на чертежах Чертеж — конструкторский документ
Чертеж — конструкторский документ Способ прямоугольных координат и перспективной сетки. Лекция 24
Способ прямоугольных координат и перспективной сетки. Лекция 24 ЕСКД. Общие правила оформления чертежей
ЕСКД. Общие правила оформления чертежей Изображения. Виды, разрезы, сечения
Изображения. Виды, разрезы, сечения Изображение и обозначение резьб
Изображение и обозначение резьб Полиэтиленовые трубки
Полиэтиленовые трубки Сопряжения
Сопряжения Резьба. Проецирование прямой линии
Резьба. Проецирование прямой линии Получение аксонометрических проекций
Получение аксонометрических проекций Проецирование группы геометрических тел
Проецирование группы геометрических тел Метод проекций. Изображения виды, разрезы, сечения. Начертательная геометрия. Компьютерная графика. Лекция 1
Метод проекций. Изображения виды, разрезы, сечения. Начертательная геометрия. Компьютерная графика. Лекция 1