ПЛАН ПРОВЕДЕНИЯ ЛЕКЦИИ № 3
Дисциплина
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ. ИНЖЕНЕРНАЯ ГРАФИКА
Раздел I
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Тема 1
раздела
ЗАДАНИЕ ТОЧКИ, ПРЯМОЙ, ПЛОСКОСТИ И МНОГОГРАННИКОВ
НА КОМПЛЕКСНОМ ЭПЮРЕ (ЧЕРТЕЖЕ) МОНЖА
Учебные цели - после изучения темы лекции студенты должны:
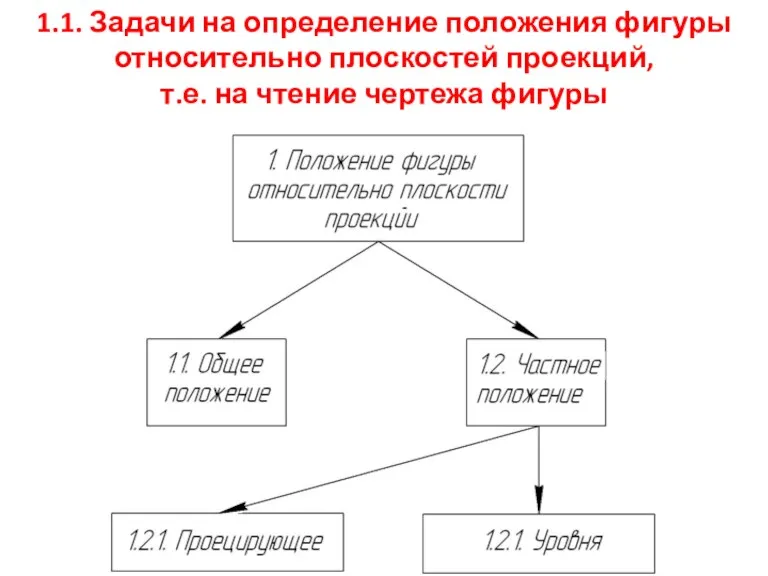
Знать классификацию позиционных задач НГ
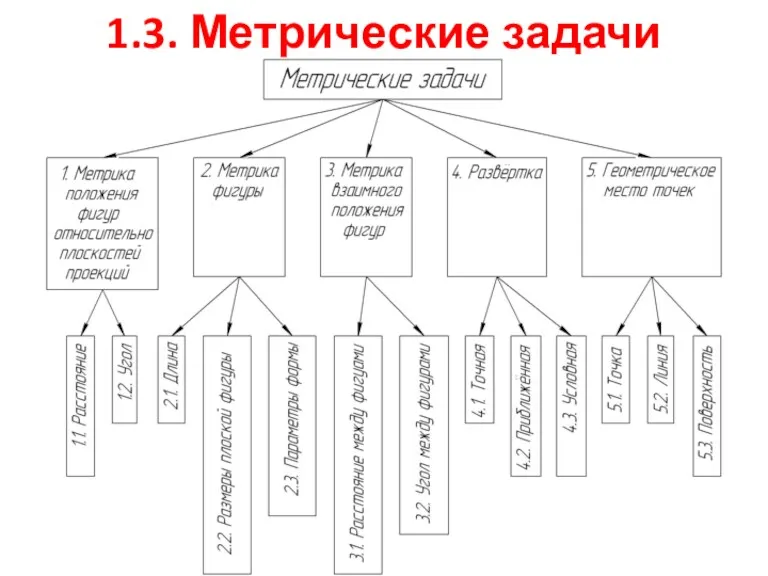
Знать классификацию метрических задач НГ
Знать способы задания прямой на эпюре
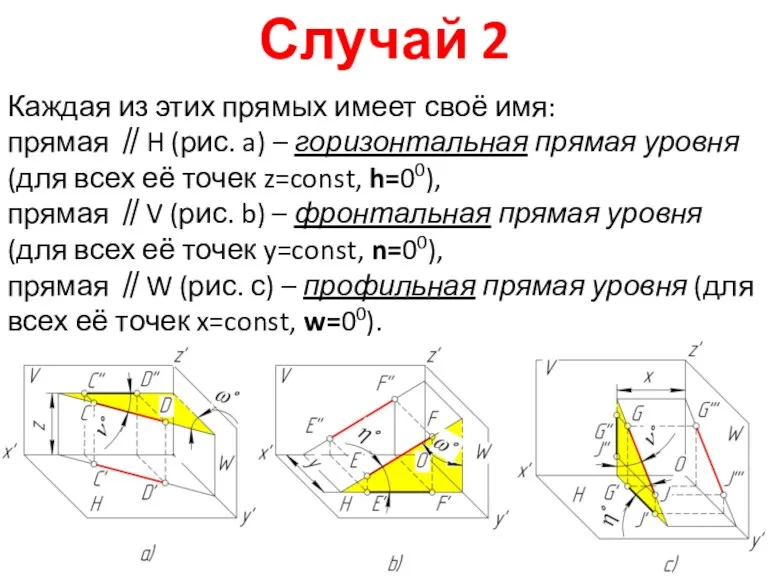
Знать три случая положения прямой относительно плоскостей проекций
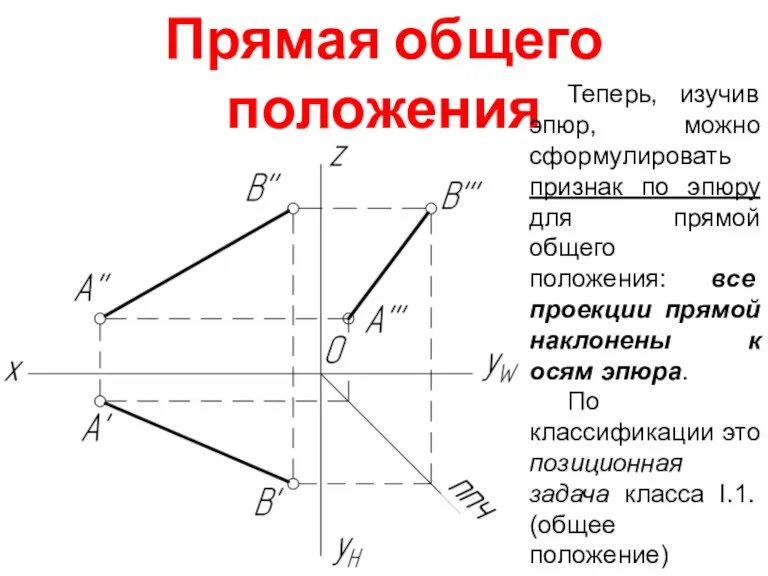
Знать признаки по эпюру для любой прямой
Учебные вопросы лекции:
Позиционные задачи
Метрические задачи
Проекции прямой
Задание на самостоятельную работу:
Изучить, понять и запомнить материал лекции 3
Рекомендуемая учебная литература:
Изучить и запомнить изложенный теоретический материал по конспекту лекций и учебнику: Фролов С.А. Начертательная геометрия: учебник.- 3-е изд., перераб и доп.- М.:ИНФРА-М, 2008.- (Высшее образование): см. с. 38-42, 139-140, 207
Тема лекции
ПОЗИЦИОННЫЕ И МЕТРИЧЕСКИЕ ЗАДАЧИ.
ЗАДАНИЕ ПРЯМОЙ НА ЭПЮРЕ МОНЖА










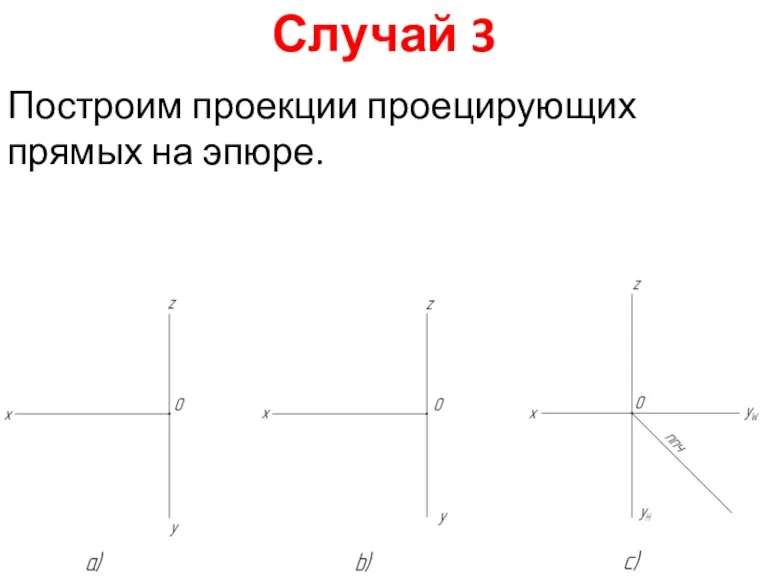


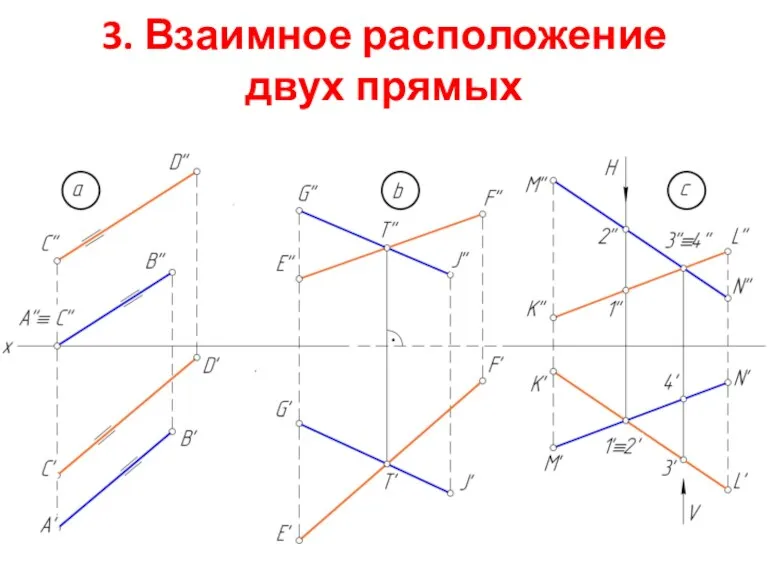
 Построение перспективы архитектурных деталей по одной точке схода (2 способ архитекторов)
Построение перспективы архитектурных деталей по одной точке схода (2 способ архитекторов) Создание крышки редуктора
Создание крышки редуктора Виды аксонометрии
Виды аксонометрии Дисциплина начертательная геометрия
Дисциплина начертательная геометрия Деление окружности на 3, 4, 6 и 8 равных частей
Деление окружности на 3, 4, 6 и 8 равных частей Болтовое соединение
Болтовое соединение Проекционное черчение. Методы проецирования
Проекционное черчение. Методы проецирования Правила выполнения рабочей документации автоматизации технологических процессов
Правила выполнения рабочей документации автоматизации технологических процессов Особые случаи разрезов
Особые случаи разрезов Основные сведения по оформлению чертежей
Основные сведения по оформлению чертежей Аксонометрические проекции. Урок 1
Аксонометрические проекции. Урок 1 Индивидуальные задания по технологии. Тема: Проецирование
Индивидуальные задания по технологии. Тема: Проецирование Портфолио. Архитектурная графика. Изображение архитектурного замысла при проектировании
Портфолио. Архитектурная графика. Изображение архитектурного замысла при проектировании Технический рисунок
Технический рисунок Дисциплина:Современное проектирование зданий и сооружений. Основные параметры
Дисциплина:Современное проектирование зданий и сооружений. Основные параметры Архитектурно-строительное черчение
Архитектурно-строительное черчение Операционализация исследования
Операционализация исследования Порядок чтения чертежей деталей
Порядок чтения чертежей деталей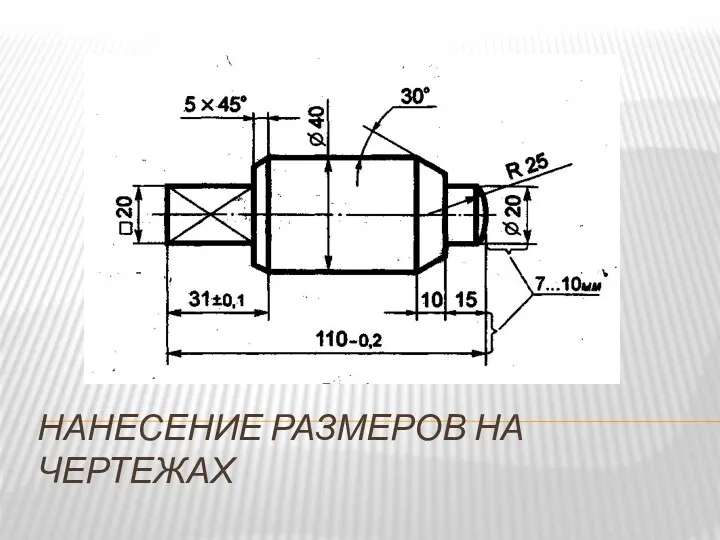 Нанесение размеров на чертежах
Нанесение размеров на чертежах Условности и упрощения на чертежах
Условности и упрощения на чертежах Сечения. Правила выполнения
Сечения. Правила выполнения Обозначение шероховатости поверхностей на чертежах
Обозначение шероховатости поверхностей на чертежах Архитектура. Построение плана здания
Архитектура. Построение плана здания Построение перспективы объекта методом архитекторов с недоступной точкой схода
Построение перспективы объекта методом архитекторов с недоступной точкой схода Сечения
Сечения Плоскость. Следы плоскости. Частное положение плоскости. Главные линии плоскости. Взаимное положение двух плоскостей
Плоскость. Следы плоскости. Частное положение плоскости. Главные линии плоскости. Взаимное положение двух плоскостей Аксонометрические проекции окружностей. 8 класс
Аксонометрические проекции окружностей. 8 класс Пересечение поверхностей вращения плоскостями
Пересечение поверхностей вращения плоскостями