Содержание
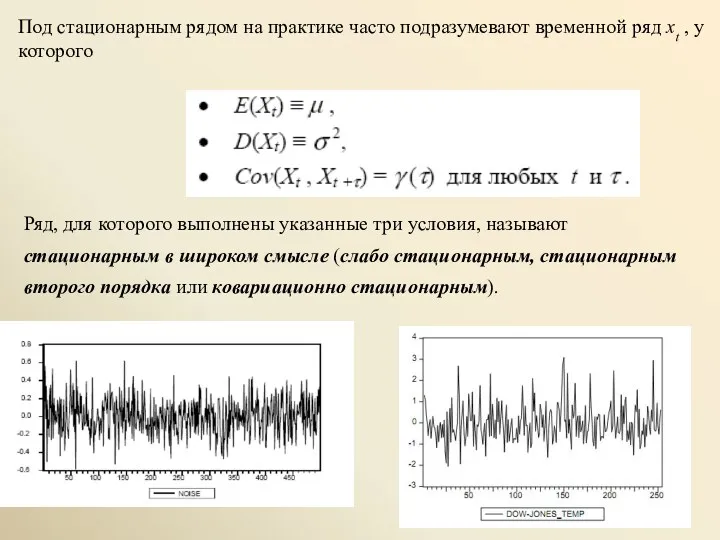
- 2. Под стационарным рядом на практике часто подразумевают временной ряд xt , у которого Ряд, для которого
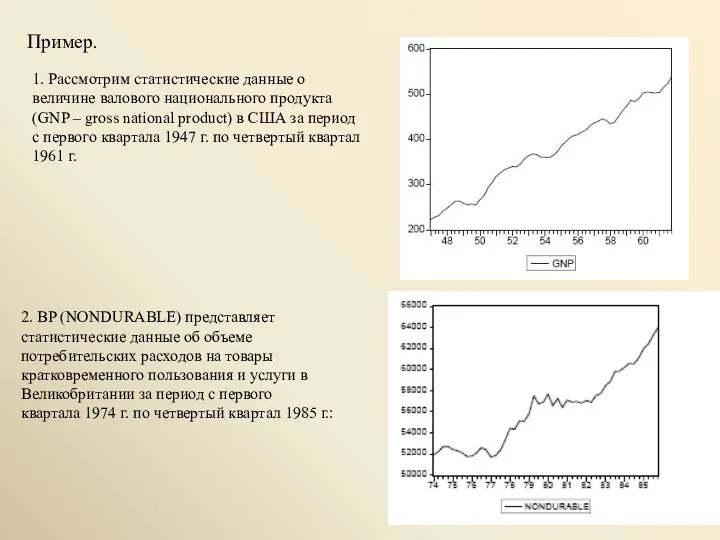
- 3. Пример. 1. Рассмотрим статистические данные о величине валового национального продукта (GNP – gross national product) в
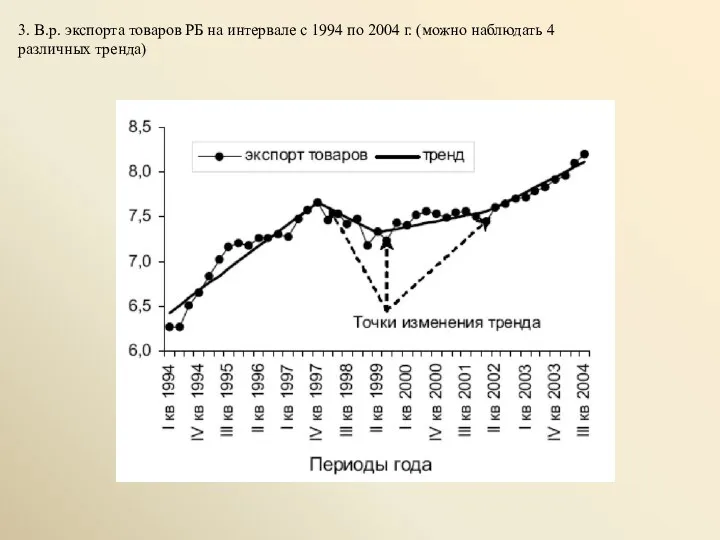
- 4. 3. В.р. экспорта товаров РБ на интервале с 1994 по 2004 г. (можно наблюдать 4 различных
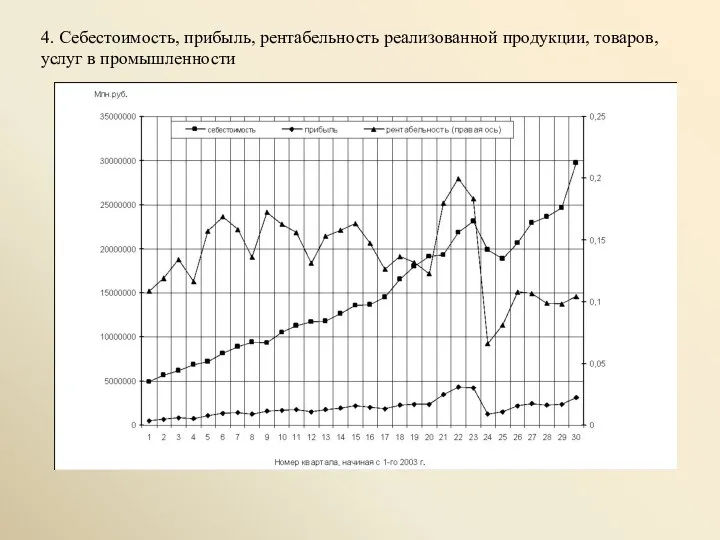
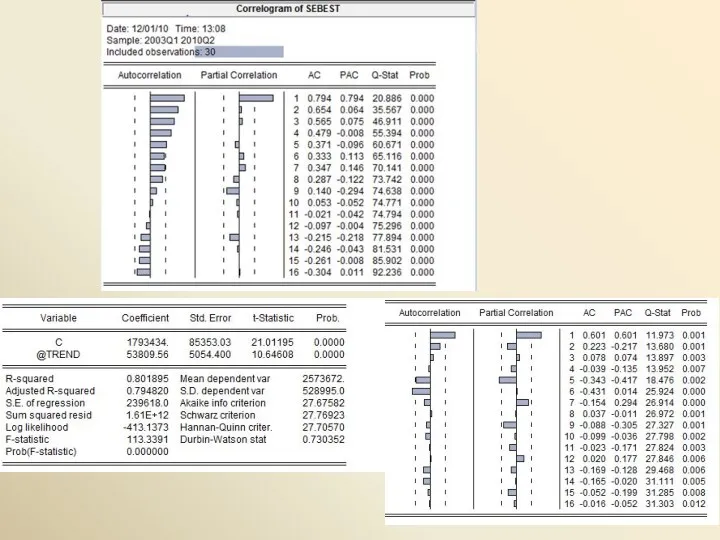
- 5. 4. Себестоимость, прибыль, рентабельность реализованной продукции, товаров, услуг в промышленности
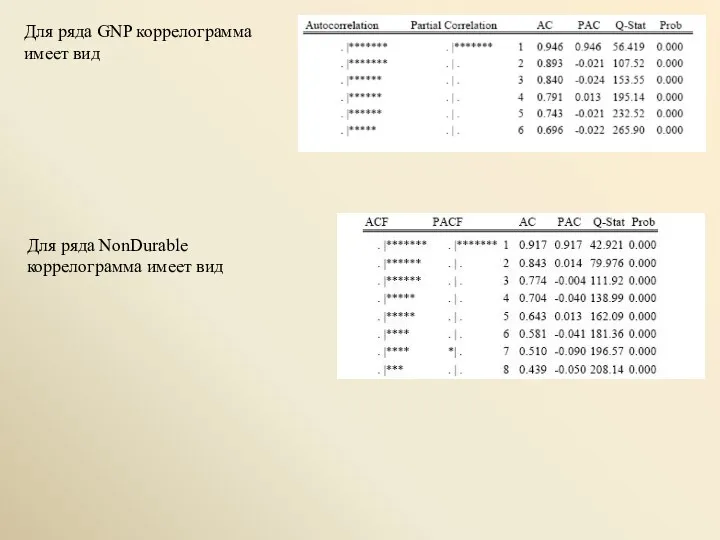
- 7. Для ряда GNP коррелограмма имеет вид Для ряда NonDurable коррелограмма имеет вид
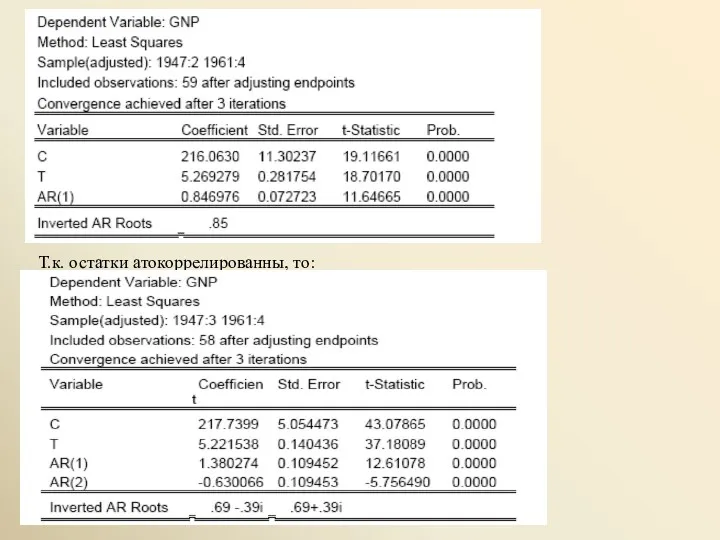
- 8. Приводимые в таблицах оценки константы (C) и коэффициента при переменной t (T) соответствуют оценкам µ и
- 9. Т.к. остатки атокоррелированны, то:
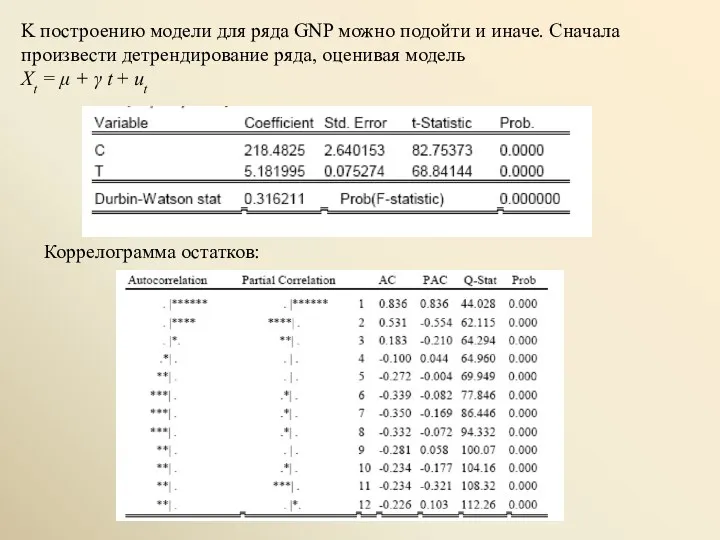
- 10. K построению модели для ряда GNP можно подойти и иначе. Сначала произвести детрендирование ряда, оценивая модель
- 11. позволяет идентифицировать этот ряд как AR(2). После этого можно строить AR(2) модель для (оцененного) детрендированного ряда
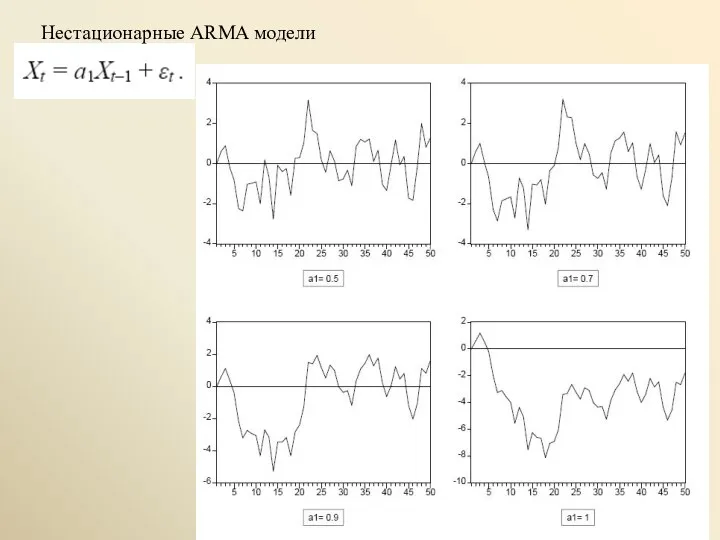
- 12. Нестационарные ARMA модели
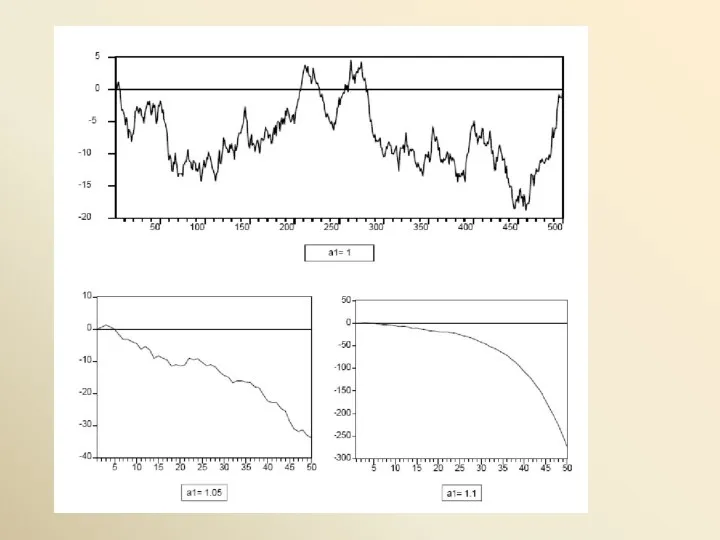
- 15. случайное блуждание (процесс случайного блуждания – random walk).
- 16. Рассмотрим процесс AR(1): Xt = a1Xt–1 + εt Представим его в виде: Xt – Xt–1 =
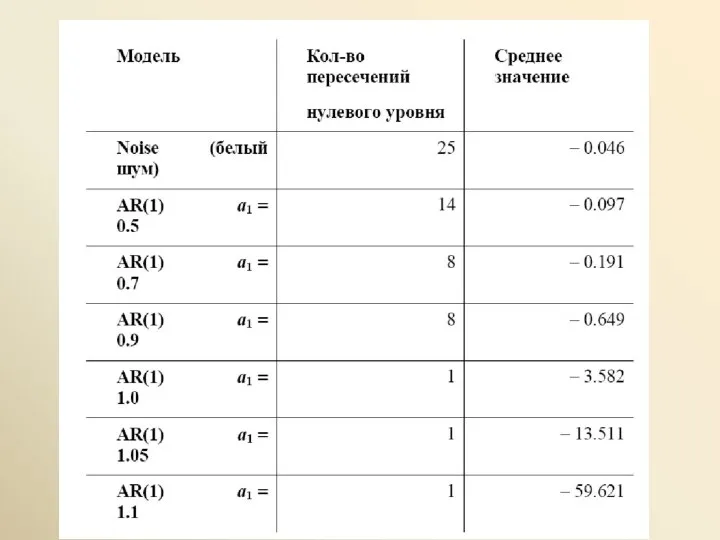
- 17. При 0 0, то ожидаемое значение следующего наблюдения Xt = xt меньше значения xt–1 , а
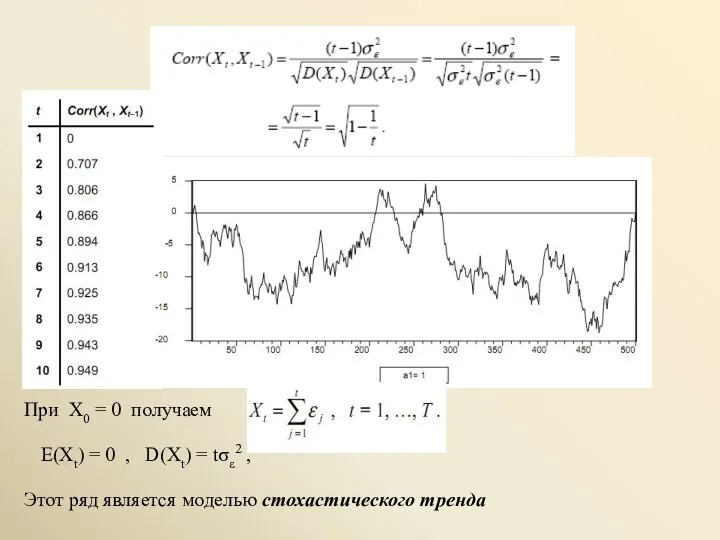
- 18. Этот ряд является моделью стохастического тренда При X0 = 0 получаем E(Xt) = 0 , D(Xt)
- 19. Различие между временными рядами, имеющими только детерминированный тренд, и рядами, которые (возможно, наряду с детерминированным) имеют
- 20. Детрендирование первого ряда приводит к ряду Xt0 = Xt – (α+ β t) = εt -
- 21. Временной ряд Xt называется стационарным относительно детерминированного тренда f(t) , если ряд Xt – f(t) стационарный.
- 22. Для интегрированного ряда порядка k используют обозначение I(k) . Если ряд Xt является интегрированным порядка k
- 23. Xt = α + β t + εt ~ I(0); Xt = α + Xt–1+ εt
- 24. Использование в регрессии нестационарных В.р. Может привести к фиктивным результатам – ложной (spurious) линейной связи, которая
- 25. Тесты на стационарность В тесте Дики-Фуллера нулевой (альтернативной) гипотезой является тот факт, что исследуемый В.р. xt
- 26. Методом наименьших квадратов оцениваются параметры модели ϕ , α , β и вычисляется значение t-статистики tϕ
- 27. В тесте Филлипса-Перрона (РР-тест) проверка нулевой гипотезы о нестационарности В.р. xt сводится к проверке гипотезы ϕ
- 28. Для λ 2 можно взять оценку – j-ая выборочная автоковариация В.р. ut, l - количество используемых
- 29. Тест Квятковского-Филлипса-Шмидта-Шина (KPSS-тест) в качестве нулевой рассматривает гипотезу о принадлежности В.р. классу стационарных. Рассмотрение ведется в
- 30. где σ2u – дисперсия остатков регрессии, e t– остатки регрессии x t на константу и тренд
- 31. Оценивание качества моделей и точности прогнозов. Для оценки качества построенных эконометрических моделей, как правило,используется стандартная техника
- 32. При использовании таблиц критических значений статистических оценок, в частности статистики DW, F-статистики, а также для оценки
- 34. Скачать презентацию



















 Мотивация результатов труда и поведения персонала организации (на материалах ИП TEHNO-Z )
Мотивация результатов труда и поведения персонала организации (на материалах ИП TEHNO-Z ) Европейский союз (ЕС)
Европейский союз (ЕС) Ключевые категории микроэкономики. Понятие и детерминанты рыночного спроса и предложения. Равновесие
Ключевые категории микроэкономики. Понятие и детерминанты рыночного спроса и предложения. Равновесие Макроэкономические проблемы: инфляция и безработица (часть 1)
Макроэкономические проблемы: инфляция и безработица (часть 1) Мировое хозяйство и международная торговля. (Обществознание. 8 класс)
Мировое хозяйство и международная торговля. (Обществознание. 8 класс) Лекция № 13. Экономический рост и экономический цикл
Лекция № 13. Экономический рост и экономический цикл Глобальные проблемы человечества
Глобальные проблемы человечества Экономическая информация. Классификация информации. Безтекстовые и текстовые формы интерпретации
Экономическая информация. Классификация информации. Безтекстовые и текстовые формы интерпретации Теория производства фирмы. Тема 4
Теория производства фирмы. Тема 4 Международное регулирование туристской деятельности
Международное регулирование туристской деятельности Ўқитишда модулли ёндашувнинг долзарблиги
Ўқитишда модулли ёндашувнинг долзарблиги Таможенно-тарифное регулирование Внешнеторговой деятельности
Таможенно-тарифное регулирование Внешнеторговой деятельности Экономические расчеты в ВКР
Экономические расчеты в ВКР Особенности калькулирования себестоимости
Особенности калькулирования себестоимости II заседание Ассоциации молодых депутатов в Янаульском районе
II заседание Ассоциации молодых депутатов в Янаульском районе Спрос. Величина спроса
Спрос. Величина спроса Перспективы развития мирового транспорта
Перспективы развития мирового транспорта Стратегия развития башкирского народа. Башҡорт халҡын һаҡлап ҡалыу юлдары (часть 3)
Стратегия развития башкирского народа. Башҡорт халҡын һаҡлап ҡалыу юлдары (часть 3) Основы теории поведения потребителя
Основы теории поведения потребителя Умный город, Череповец, 2019
Умный город, Череповец, 2019 Формы интеграционных объединений
Формы интеграционных объединений Адам даму индексі
Адам даму индексі 第7章 市场失灵与宏观经济学概论
第7章 市场失灵与宏观经济学概论 Экономика. Бюджет
Экономика. Бюджет Антиинфляционная политика государства
Антиинфляционная политика государства Финансово-экономические характеристики деятельности публичных компаний
Финансово-экономические характеристики деятельности публичных компаний Инвестиционные риски. Характеристики методов учета неопределенности инвестиционного проекта. (Тема 9)
Инвестиционные риски. Характеристики методов учета неопределенности инвестиционного проекта. (Тема 9) Постиндустриальное (информационное) общество
Постиндустриальное (информационное) общество