Содержание
- 2. 3. Векторное поле (продолжение) ОПРЕДЕЛЕНИЕ Векторное поле определяется векторной функцией точки где - точка пространства; -
- 3. 3. Векторное поле (продолжение) Векторная линия Векторная линия (силовая линия, линия тока) поля это кривая, у
- 4. 3. Векторное поле Векторная линия (продолжение) © Бутырин В.И., Гобыш А.В., Филатов В.В., Шварц Э.Б. 2016
- 5. 3. Векторное поле (продолжение) Дивергенция Дивергенция (расходимость) векторного поля © Бутырин В.И., Гобыш А.В., Филатов В.В.,
- 6. 3. Векторное поле Дивергенция (продолжение) Свойства дивергенции © Бутырин В.И., Гобыш А.В., Филатов В.В., Шварц Э.Б.
- 7. 3. Векторное поле (продолжение) Ротор Ротор (вихрь) векторного поля или в символическом виде © Бутырин В.И.,
- 8. 3. Векторное поле Ротор (продолжение) Свойства ротора © Бутырин В.И., Гобыш А.В., Филатов В.В., Шварц Э.Б.
- 9. 3. Векторное поле (продолжение) Поток векторного поля Поток векторного поля через поверхность в сторону, определяемую единичным
- 10. Поток П вектора есть скалярная величина. Величина П равна объему жидкости, которая протекает через поверхность за
- 11. Физически величину потока П через замкнутую поверхность можно трактовать как разность между количеством жидкости, вытекающей из
- 12. 3. Векторное поле Поток векторного поля (продолжение) © Бутырин В.И., Гобыш А.В., Филатов В.В., Шварц Э.Б.
- 13. 3. Векторное поле Поток векторного поля (продолжение) © Бутырин В.И., Гобыш А.В., Филатов В.В., Шварц Э.Б.
- 14. 3. Векторное поле Поток векторного поля (продолжение) Связь дивергенции с потоком векторного поля : где -
- 15. 3. Векторное поле Поток векторного поля (продолжение) Если поверхность задана уравнением поток через верхнюю сторону поверхности
- 16. 3. Векторное поле Поток векторного поля (продолжение) Если уравнение поверхности есть то © Бутырин В.И., Гобыш
- 17. 3. Векторное поле (продолжение) Линейный интеграл от вектора по линии где - проекция вектора на касательную
- 18. 3. Векторное поле (продолжение) Циркуляция Циркуляция векторного поля вдоль контура - линейный интеграл вдоль замкнутой линии
- 19. 3. Векторное поле Циркуляция (продолжение) © Бутырин В.И., Гобыш А.В., Филатов В.В., Шварц Э.Б. 2016
- 20. 3. Векторное поле Циркуляция (продолжение) © Бутырин В.И., Гобыш А.В., Филатов В.В., Шварц Э.Б. 2016
- 21. 3. Векторное поле (продолжение) Связь ротора векторного поля с циркуляцией определяется формулой лежит в плоскости, перпендикулярной
- 22. 3. Векторное поле (продолжение) Формула Гаусса-Остроградского Теорема. Если векторная функция непрерывна в замкнутой правильной области вместе
- 23. 3. Векторное поле Формула Гаусса-Остроградского (продолжение) или в векторной форме где - внешняя сторона поверхности, ограничивающей
- 24. 3. Векторное поле (продолжение) Формула Стокса Теорема. Пусть - поверхностно-односвязная область, - кусочно-гладкий контур в и
- 25. 3. Векторное поле Формула Стокса (продолжение) В декартовой системе координат формула Стокса примет вид © Бутырин
- 27. Скачать презентацию
























 Открытие протона и нейтрона. 9 класс
Открытие протона и нейтрона. 9 класс Молекулярная физика и термодинамика
Молекулярная физика и термодинамика Передаточные функции и частотные характеристики АС
Передаточные функции и частотные характеристики АС Особенности распространения радиоволн коротковолнового диапазона
Особенности распространения радиоволн коротковолнового диапазона Силы сопротивления при движении твердых тел в жидкостях и газах
Силы сопротивления при движении твердых тел в жидкостях и газах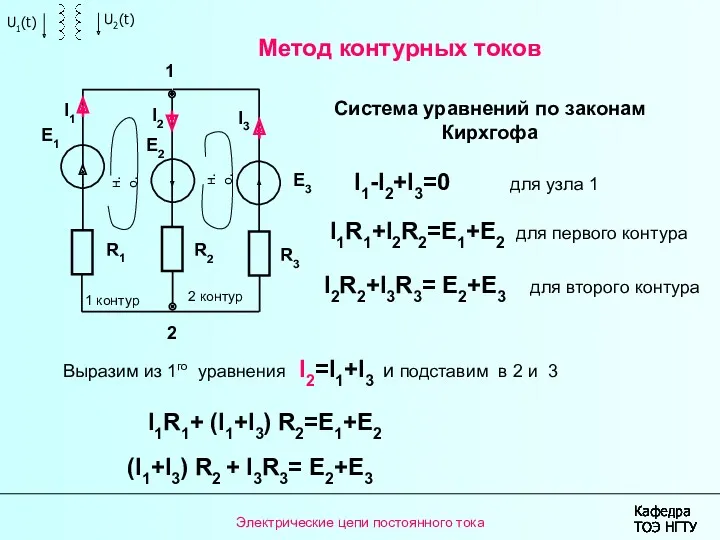 Метод контурных токов
Метод контурных токов Электрические явления
Электрические явления Закон Ома для полной цепи
Закон Ома для полной цепи Елементи спеціальної теорії відносності
Елементи спеціальної теорії відносності Физика и техника (7 класс)
Физика и техника (7 класс) Прохождение частицы через потенциальный барьер. Уравнение Шредингера для водородоподобного атома. Квантовые числа
Прохождение частицы через потенциальный барьер. Уравнение Шредингера для водородоподобного атома. Квантовые числа Электромагнитные колебания. Колебательный контур
Электромагнитные колебания. Колебательный контур Простые механизмы
Простые механизмы Что такое энергия
Что такое энергия Элементы машиноведения. Составные части машин
Элементы машиноведения. Составные части машин Презентация к уроку Значение влажности
Презентация к уроку Значение влажности ГАЗ 31029: Механика, технические характеристики, комплектация
ГАЗ 31029: Механика, технические характеристики, комплектация Энергетические уровни. Спонтанное и вынужденное излучения. Лекция 2
Энергетические уровни. Спонтанное и вынужденное излучения. Лекция 2 Скорость света
Скорость света Радиоактивность. (9 класс)
Радиоактивность. (9 класс) презентация к уроку физики 11 класс
презентация к уроку физики 11 класс Сила Лоренца
Сила Лоренца Математические модели установившегося режима и методы решения. Общие сведения о схемах замещения
Математические модели установившегося режима и методы решения. Общие сведения о схемах замещения Экзамен ПМ 01. Билет № 3. Методы производства такелажных работ
Экзамен ПМ 01. Билет № 3. Методы производства такелажных работ Розв’язування задач з теми Механічна робота. Потужність
Розв’язування задач з теми Механічна робота. Потужність Генерирование электрического тока. Трансформатор
Генерирование электрического тока. Трансформатор Физика и познание мира
Физика и познание мира Колебания и волны. Квантовая физика
Колебания и волны. Квантовая физика