Содержание
- 2. Дифференциальное уравнение теплопроводности
- 3. Метод математической физики Для вывода дифференциального уравнения теплопроводности используется метод математической физики, когда процесс изучается в
- 4. Допущения ● изменение объема тела от температуры пренебрежимо мало, по сравнению с его объемом, как величина
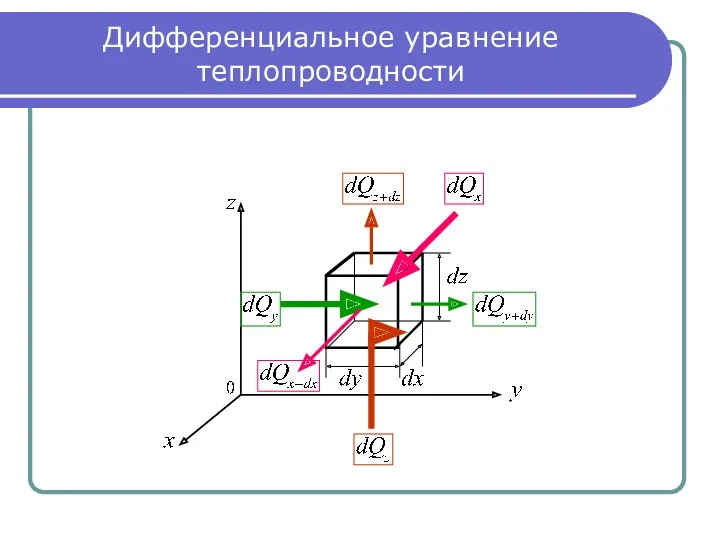
- 5. Уравнения (3 – 7) тепловыделения внутренних источников: ; (3) теплота, вошедшая теплопроводностью в элементарный объем dv
- 6. Уравнения (8 - 11) Функцию можно разложить в ряд Тейлора: . (8) Пренебрегаем величиной 2 порядка
- 7. Уравнения (12 – 13) Уравнения (9), (10), (11) подставляем в (4): , (12) а уравнения (2),
- 8. Уравнения (14 – 17) Производные от тепловых потоков по координатам: . (14) После подстановки (14) в
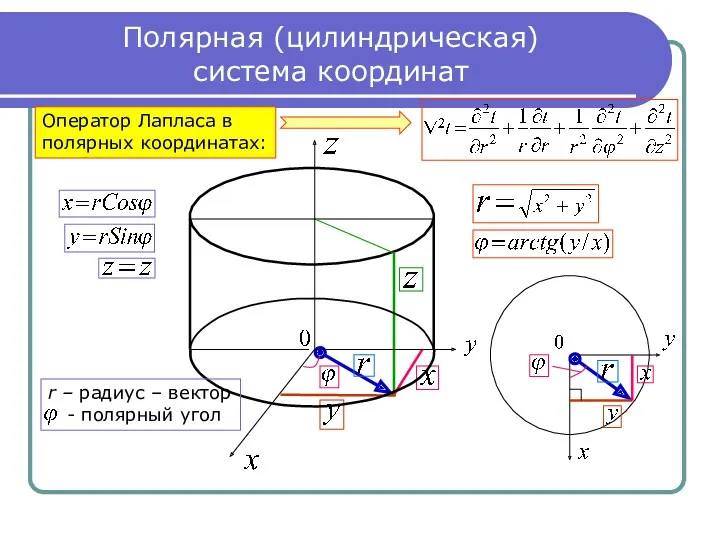
- 9. Полярная (цилиндрическая) система координат Оператор Лапласа в полярных координатах: r – радиус – вектор - полярный
- 10. Условия однозначности Дифференциальное уравнение теплопроводности (17) справедливо для ортогональных и полярных координат, с учетом выражений операторов
- 11. Граничные условия I рода: , для стационарных процессов они принимают вид: . II рода: , или
- 13. Скачать презентацию








 Физическая и коллоидная химия
Физическая и коллоидная химия Кінетична потенціальна енергія
Кінетична потенціальна енергія Формирование учебно-познавательной компетенции учащихся второй ступени обучения на уроках физики
Формирование учебно-познавательной компетенции учащихся второй ступени обучения на уроках физики Электрические явления. Соединения проводников
Электрические явления. Соединения проводников Сверхпроводимость
Сверхпроводимость Зубчатые передачи
Зубчатые передачи Полевая геофизика. Магниторазведка (лекция 2 )
Полевая геофизика. Магниторазведка (лекция 2 ) Механизмы управления. Рулевое управление
Механизмы управления. Рулевое управление Распределение газовых молекул по скоростям и энергиям
Распределение газовых молекул по скоростям и энергиям Механические колебания
Механические колебания Преломление света. Физический смысл показателя преломления. 9 класс
Преломление света. Физический смысл показателя преломления. 9 класс Мосты грузовых автомобилей МАЗ
Мосты грузовых автомобилей МАЗ Типовые примеры сборки узлов и панелей клепанной конструкции
Типовые примеры сборки узлов и панелей клепанной конструкции Урок-игра по волновой оптике
Урок-игра по волновой оптике Презентация к уроку Вес тела. 7 класс.
Презентация к уроку Вес тела. 7 класс. Электрические цепи постоянного тока (продолжение)
Электрические цепи постоянного тока (продолжение) Изготовление столярного соединения УС-1
Изготовление столярного соединения УС-1 Последовательное ипараллельное соединение. Электрические явления
Последовательное ипараллельное соединение. Электрические явления Сұйықтардың беттік керілуі
Сұйықтардың беттік керілуі Лекция № 5,6 РБ. Цепная реакция деления тяжелых ядер
Лекция № 5,6 РБ. Цепная реакция деления тяжелых ядер Волновая теория света
Волновая теория света Система автоматического управления
Система автоматического управления Игра Кто хочет стать физиком для 7 - 8 классов
Игра Кто хочет стать физиком для 7 - 8 классов Гидравлика. Физические свойства жидкостей
Гидравлика. Физические свойства жидкостей Оптическая литография
Оптическая литография Решение задач по теме Основы термодинамики
Решение задач по теме Основы термодинамики Воздействие лазерного излучения на мишени
Воздействие лазерного излучения на мишени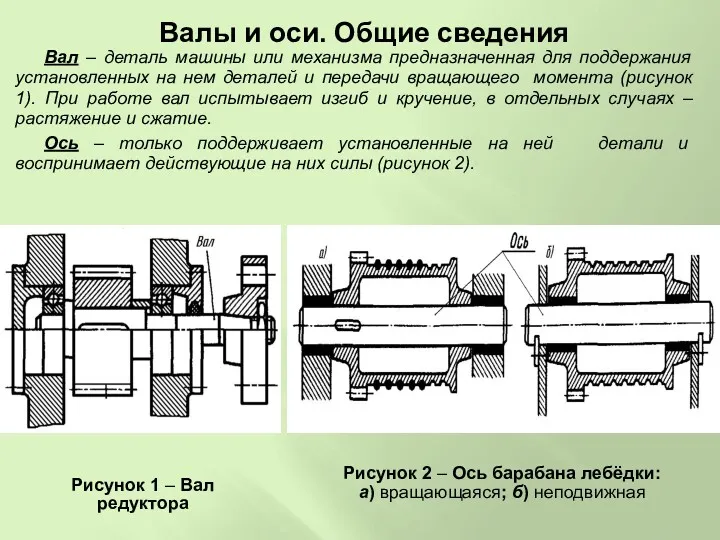 Валы и оси машины или механизма
Валы и оси машины или механизма