Содержание
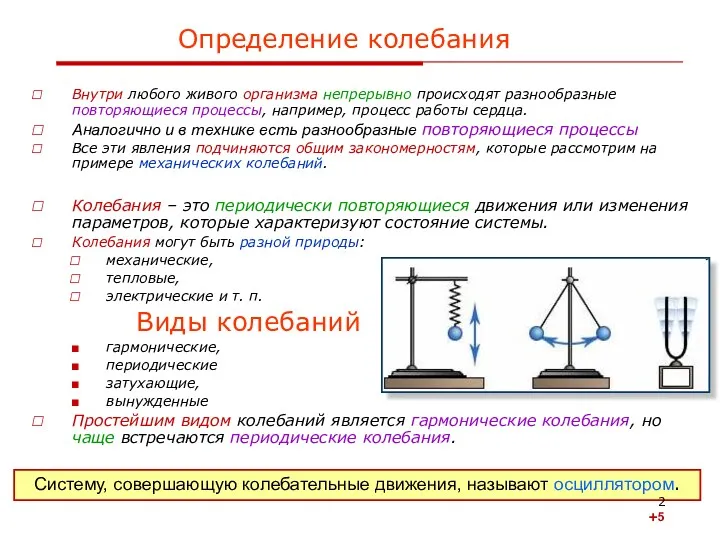
- 2. Определение колебания Внутри любого живого организма непрерывно происходят разнообразные повторяющиеся процессы, например, процесс работы сердца. Аналогично
- 3. Основные характеристики колебательного движения Смещение x – это расстояние, на которое отклоняется колеблющееся тело в данный
- 4. Основные характеристики колебательного движения (продолжение) Циклическая или круговая частота ω («омега») – величина, которая связана с
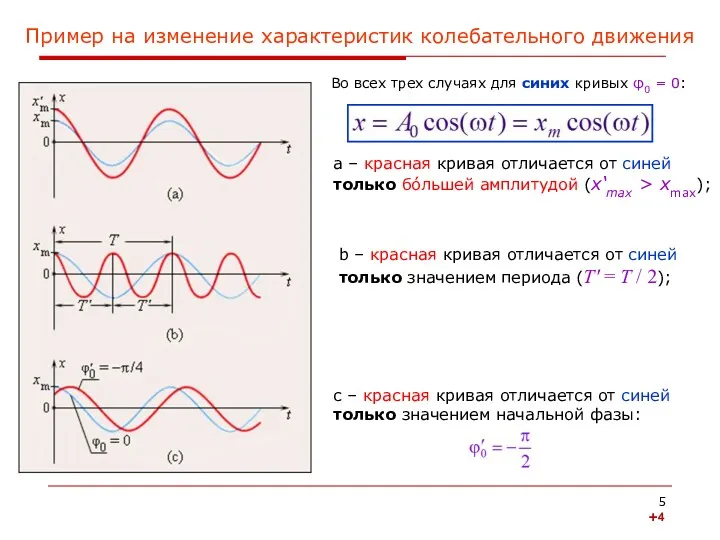
- 5. Пример на изменение характеристик колебательного движения Во всех трех случаях для синих кривых φ0 = 0:
- 6. Основные характеристики колебательного движения (ещё продолжение) Скорость движения материальной точки v. Измеряется в СИ в метрах
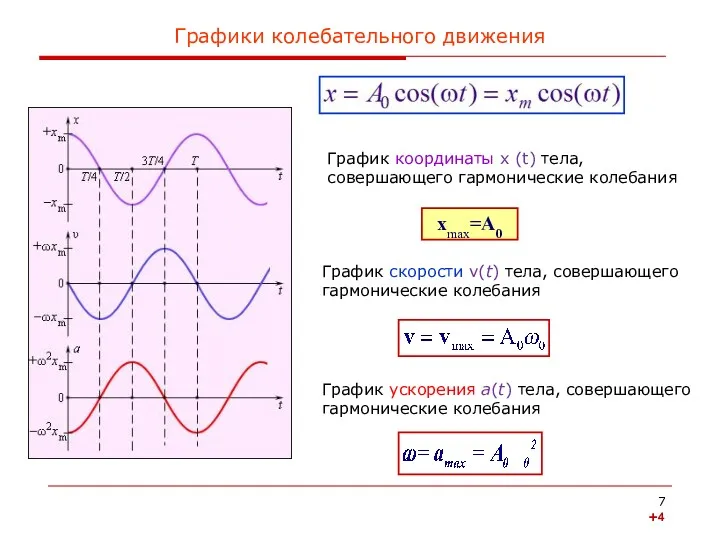
- 7. Графики колебательного движения График координаты x (t) тела, совершающего гармонические колебания График скорости v(t) тела, совершающего
- 8. Энергия гармонического колебания Полная энергия гармонического колебания E определяется суммой кинетической и потенциальной энергий: Подставляя в
- 9. Маятники Маятник − это тело массой m, , подвешенная на нити или пружине и совершающее гармонические
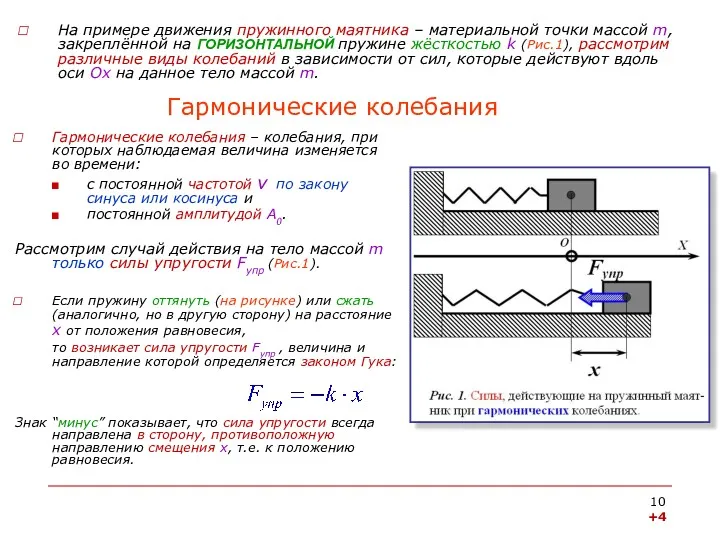
- 10. Гармонические колебания Гармонические колебания – колебания, при которых наблюдаемая величина изменяется во времени: с постоянной частотой
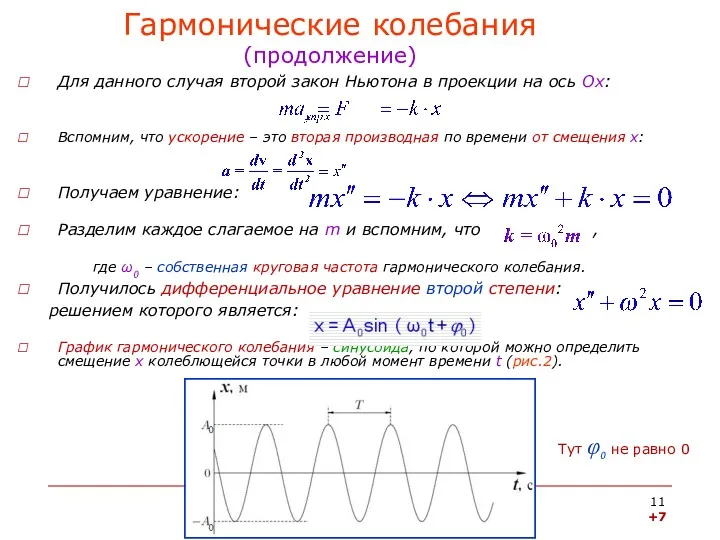
- 11. Гармонические колебания (продолжение) Для данного случая второй закон Ньютона в проекции на ось Ох: Вспомним, что
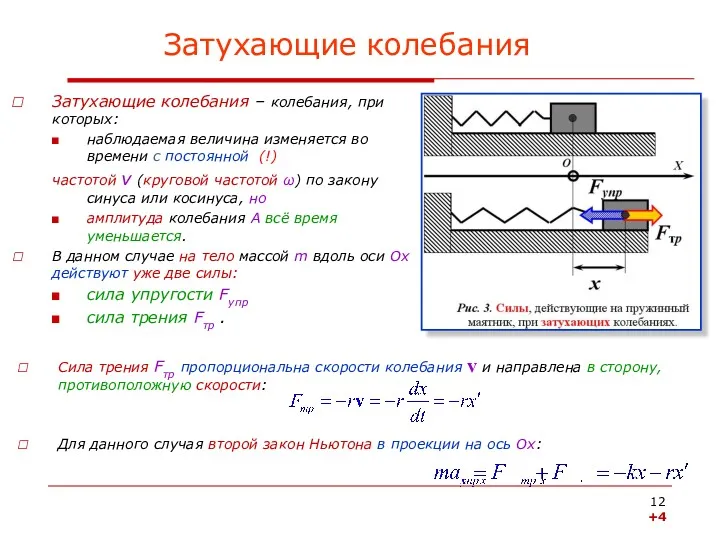
- 12. Затухающие колебания Затухающие колебания – колебания, при которых: наблюдаемая величина изменяется во времени с постоянной (!)
- 13. Затухающие колебания (продолжение) Учтём, что: Тогда при сокращении каждого слагаемого на m и переносе всех членов
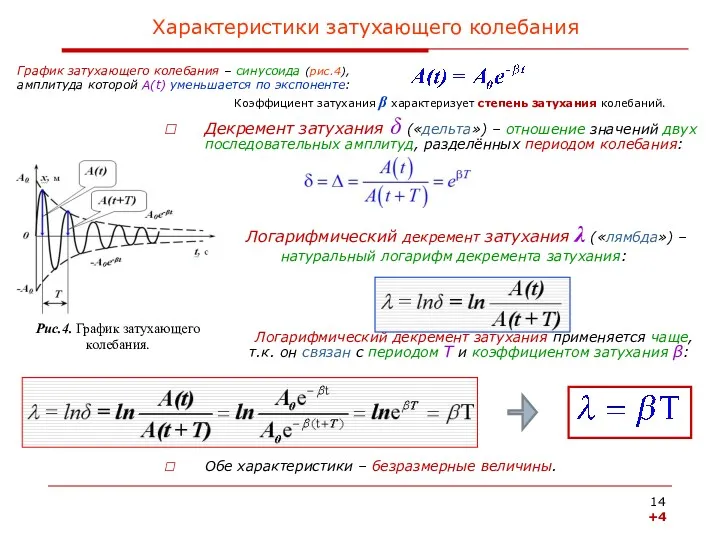
- 14. Декремент затухания δ («дельта») – отношение значений двух последовательных амплитуд, разделённых периодом колебания: Логарифмический декремент затухания
- 15. Время релаксации τ («тау») – это время, за которое амплитуда уменьшается в e раз: Характеристики затухающего
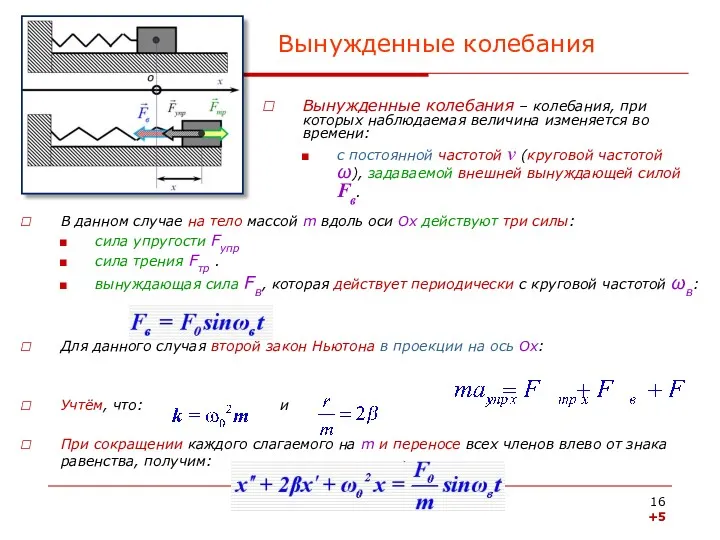
- 16. В данном случае на тело массой m вдоль оси Ох действуют три силы: сила упругости Fупр
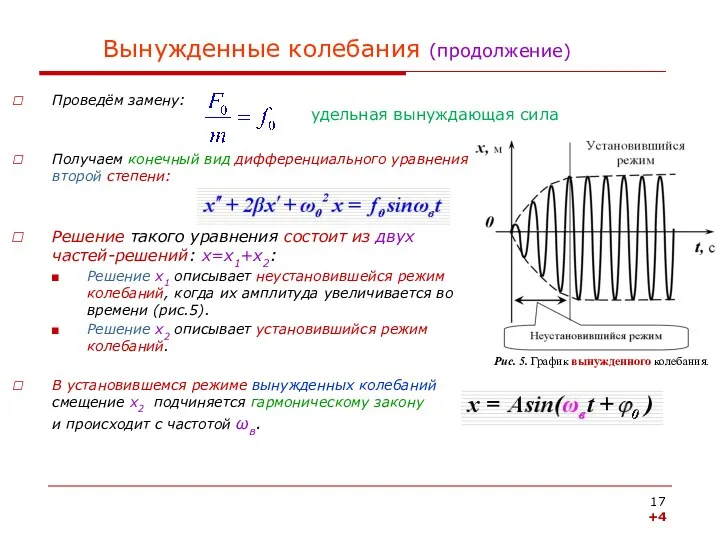
- 17. Вынужденные колебания (продолжение) Проведём замену: Получаем конечный вид дифференциального уравнения второй степени: Решение такого уравнения состоит
- 18. Резонанс Амплитуда А вынужденных колебаний зависит от многих разобранных выше параметров: частоты собственных колебаний ω0 ,
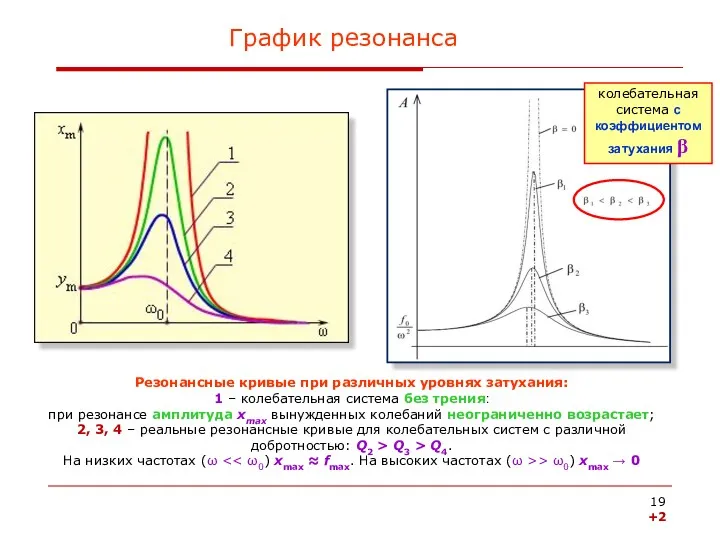
- 19. График резонанса Резонансные кривые при различных уровнях затухания: 1 – колебательная система без трения: при резонансе
- 21. Скачать презентацию








 Презентация урока по теме Количество теплоты
Презентация урока по теме Количество теплоты Хроматографические методы. (Часть 2)
Хроматографические методы. (Часть 2) Редуктор конический одноступенчатый горизонтальный
Редуктор конический одноступенчатый горизонтальный Термодинамика. Основы термодинамики
Термодинамика. Основы термодинамики Сабақтың тақырыбы Электр тогының жұмысы мен қуаты. Джоуль –Ленц заңы. Ток көзінің пайдалы әсер коэффициенті
Сабақтың тақырыбы Электр тогының жұмысы мен қуаты. Джоуль –Ленц заңы. Ток көзінің пайдалы әсер коэффициенті Буксовый узел грузового вагона. Техническая ревизия буксового узла колесный пары РУ1-Ш
Буксовый узел грузового вагона. Техническая ревизия буксового узла колесный пары РУ1-Ш What is the brake calipers?
What is the brake calipers? Полярография. Ртутно-капающий электрод. Роль метода в медицине и фармации
Полярография. Ртутно-капающий электрод. Роль метода в медицине и фармации Сила Лоренца
Сила Лоренца сила упругости
сила упругости Своя игра. Физика. 7 класс.
Своя игра. Физика. 7 класс. Электромагнитные колебания
Электромагнитные колебания Радиоактивность. Виды радиоактивных излучений. Изотопы. Закон радиоактивного распада. Радиоактивность вокруг нас
Радиоактивность. Виды радиоактивных излучений. Изотопы. Закон радиоактивного распада. Радиоактивность вокруг нас Трехфазные цепи переменного тока
Трехфазные цепи переменного тока Энергия топлива- урок физики в 8 классе
Энергия топлива- урок физики в 8 классе Влияние на работу дороги природных факторов
Влияние на работу дороги природных факторов Жұмыс орындарындағы электромагниттік сәулеленулер
Жұмыс орындарындағы электромагниттік сәулеленулер Скорость света
Скорость света Електричний струм у газах. Самостійний і несамостійний газові розряди. Плазма
Електричний струм у газах. Самостійний і несамостійний газові розряди. Плазма Основные законы идеального газа
Основные законы идеального газа Механика. Основные понятия кинематики
Механика. Основные понятия кинематики Аеродинаміка та динаміка польоту літака. Аеродинамічні характеристики крила. (Лекція 5.2.1)
Аеродинаміка та динаміка польоту літака. Аеродинамічні характеристики крила. (Лекція 5.2.1) Совершенствование коробки передач автомобиля УАЗ ПАТРИОТ
Совершенствование коробки передач автомобиля УАЗ ПАТРИОТ Метод кругового дихроизма и дисперсии оптического вращения
Метод кругового дихроизма и дисперсии оптического вращения Constraints application. Solution and computation of reactions, displacements, rotations, stresses and strains. 19 lesson
Constraints application. Solution and computation of reactions, displacements, rotations, stresses and strains. 19 lesson Рулевое управление
Рулевое управление Електричний струм у різних середовищах
Електричний струм у різних середовищах Модальный метод синтеза непрерывных систем
Модальный метод синтеза непрерывных систем