Слайд 8

Пьер Вариньон
Пьер Вариньон (фр. Pierre Varignon, Кан, Кан, 1654, Кан, 1654 — 23
декабря, Кан, 1654 — 23 декабря, 1722, Кан, 1654 — 23 декабря, 1722, Париж, Кан, 1654 — 23 декабря, 1722, Париж) — французский, Кан, 1654 — 23 декабря, 1722, Париж) — французский математик, Кан, 1654 — 23 декабря, 1722, Париж) — французский математик, член Парижской Академии наук, Кан, 1654 — 23 декабря, 1722, Париж) — французский математик, член Парижской Академии наук, профессор математики коллежа Мазарини, Кан, 1654 — 23 декабря, 1722, Париж) — французский математик, член Парижской Академии наук, профессор математики коллежа Мазарини (1688, Кан, 1654 — 23 декабря, 1722, Париж) — французский математик, член Парижской Академии наук, профессор математики коллежа Мазарини (1688), профессор Коллеж де Франс, Кан, 1654 — 23 декабря, 1722, Париж) — французский математик, член Парижской Академии наук, профессор математики коллежа Мазарини (1688), профессор Коллеж де Франс.[1], Кан, 1654 — 23 декабря, 1722, Париж) — французский математик, член Парижской Академии наук, профессор математики коллежа Мазарини (1688), профессор Коллеж де Франс.[1] Обучался в иезуитском, Кан, 1654 — 23 декабря, 1722, Париж) — французский математик, член Парижской Академии наук, профессор математики коллежа Мазарини (1688), профессор Коллеж де Франс.[1] Обучался в иезуитском коллеже и университете, Кан, 1654 — 23 декабря, 1722, Париж) — французский математик, член Парижской Академии наук, профессор математики коллежа Мазарини (1688), профессор Коллеж де Франс.[1] Обучался в иезуитском коллеже и университете в Кане, Кан, 1654 — 23 декабря, 1722, Париж) — французский математик, член Парижской Академии наук, профессор математики коллежа Мазарини (1688), профессор Коллеж де Франс.[1] Обучался в иезуитском коллеже и университете в Кане, где стал магистром, Кан, 1654 — 23 декабря, 1722, Париж) — французский математик, член Парижской Академии наук, профессор математики коллежа Мазарини (1688), профессор Коллеж де Франс.[1] Обучался в иезуитском коллеже и университете в Кане, где стал магистром в 1682 году.
Вариньон был другом НьютонаВариньон был другом Ньютона, ЛейбницаВариньон был другом Ньютона, Лейбница и БернуллиВариньон был другом Ньютона, Лейбница и Бернулли. Основной вклад Вариньон совершил в статикуВариньон был другом Ньютона, Лейбница и Бернулли. Основной вклад Вариньон совершил в статику и механикуВариньон был другом Ньютона, Лейбница и Бернулли. Основной вклад Вариньон совершил в статику и механику; кроме того, труды Вариньона посвящены анализу бесконечно малыхВариньон был другом Ньютона, Лейбница и Бернулли. Основной вклад Вариньон совершил в статику и механику; кроме того, труды Вариньона посвящены анализу бесконечно малых, геометрииВариньон был другом Ньютона, Лейбница и Бернулли. Основной вклад Вариньон совершил в статику и механику; кроме того, труды Вариньона посвящены анализу бесконечно малых, геометрии, гидромеханикеВариньон был другом Ньютона, Лейбница и Бернулли. Основной вклад Вариньон совершил в статику и механику; кроме того, труды Вариньона посвящены анализу бесконечно малых, геометрии, гидромеханике. За исключением ЛопиталяВариньон был другом Ньютона, Лейбница и Бернулли. Основной вклад Вариньон совершил в статику и механику; кроме того, труды Вариньона посвящены анализу бесконечно малых, геометрии, гидромеханике. За исключением Лопиталя, Вариньон был самым первым пропагандистом дифференциального исчисленияВариньон был другом Ньютона, Лейбница и Бернулли. Основной вклад Вариньон совершил в статику и механику; кроме того, труды Вариньона посвящены анализу бесконечно малых, геометрии, гидромеханике. За исключением Лопиталя, Вариньон был самым первым пропагандистом дифференциального исчисления во Франции. В 1687 годуВариньон был другом Ньютона, Лейбница и Бернулли. Основной вклад Вариньон совершил в статику и механику; кроме того, труды Вариньона посвящены анализу бесконечно малых, геометрии, гидромеханике. За исключением Лопиталя, Вариньон был самым первым пропагандистом дифференциального исчисления во Франции. В 1687 году в своей работе «Проект новой механики…» Вариньон дал точную формулировку закона параллелограмма сил, развил понятие момента сил и вывел теорему, получившую имя Вариньона. В работе «Новая механика или статика, проект которой был дан в 1687» (1725 В работе «Новая механика или статика, проект которой был дан в 1687» (1725) Вариньон дал систематическое изложение учения о сложении и разложении сил, о моментах сил и о правилах оперирования ими.[1]






















 Плотность вещества
Плотность вещества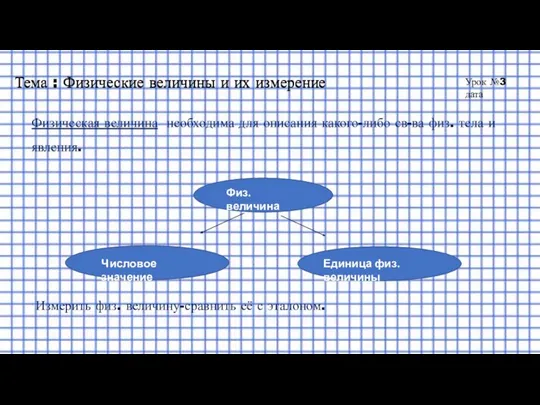 Физические величины и их измерение
Физические величины и их измерение Двигатели внутреннего сгорания. Система питания
Двигатели внутреннего сгорания. Система питания Триботехника. Определение и основные термины
Триботехника. Определение и основные термины Фізичні величини. Одиниці фізичних величин. Міжнародна система одиниць
Фізичні величини. Одиниці фізичних величин. Міжнародна система одиниць Спектрально-люминесцентные методы исследования
Спектрально-люминесцентные методы исследования Презентация к уроку Гамма - излучение.
Презентация к уроку Гамма - излучение. Надпровідність. Перспективи та застосування. Надпровідники. Лампа, діод, транзистор. Електричний струм у металах
Надпровідність. Перспективи та застосування. Надпровідники. Лампа, діод, транзистор. Електричний струм у металах Переменный электрический ток
Переменный электрический ток Дисперсия света. Интерференция. Применение интерференции. Физика. 11 класс
Дисперсия света. Интерференция. Применение интерференции. Физика. 11 класс Техническое обслуживание и ремонт автотранспорта. Устройство автомобилей
Техническое обслуживание и ремонт автотранспорта. Устройство автомобилей Законы и формулы молекулярной физики
Законы и формулы молекулярной физики Порівняння швидкостей рухів тварин, техніки
Порівняння швидкостей рухів тварин, техніки Своя игра по физике. 9 класс
Своя игра по физике. 9 класс Эксергия. Термодинамические процессы в газах, парах и их смесях. (Занятие 4)
Эксергия. Термодинамические процессы в газах, парах и их смесях. (Занятие 4) Презентация к уроку Три состояния вещества по прогр. Л.Э. Генденштейна, 7 класс
Презентация к уроку Три состояния вещества по прогр. Л.Э. Генденштейна, 7 класс Свойства и применение радиоволн. (11 класс)
Свойства и применение радиоволн. (11 класс) Элементы машиноведения. Составные части машин
Элементы машиноведения. Составные части машин Battery. Direct and Alternating current
Battery. Direct and Alternating current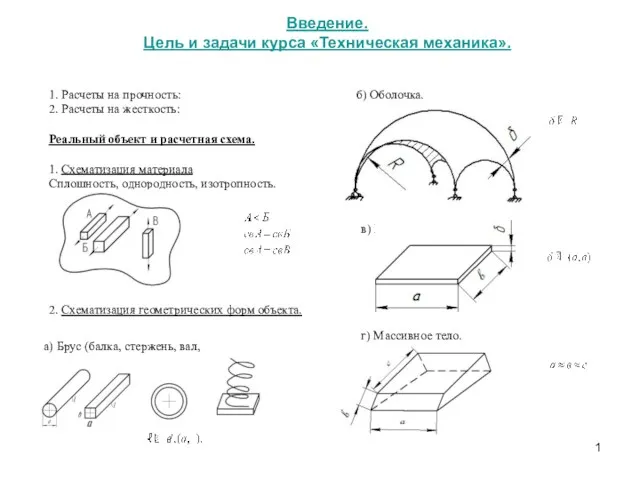 Цель и задачи курса Техническая механика. Расчеты на прочность. Расчеты на жесткость
Цель и задачи курса Техническая механика. Расчеты на прочность. Расчеты на жесткость Історія електричної лампи ( Das Geschichte des Glübirne )
Історія електричної лампи ( Das Geschichte des Glübirne ) Солнечная энергетика
Солнечная энергетика Кристаллофизикалық координат жүйесі
Кристаллофизикалық координат жүйесі Физика – наука о наиболее общих формах движения материи и их взаимных превращениях. Лекция №1
Физика – наука о наиболее общих формах движения материи и их взаимных превращениях. Лекция №1 Действие жидкости и газа на погруженное в них тело. Физика, 7 класс
Действие жидкости и газа на погруженное в них тело. Физика, 7 класс Механические колебания. Волны. Акустика
Механические колебания. Волны. Акустика Қатты дене-сұйық жанасу шегіндегі адсорбция
Қатты дене-сұйық жанасу шегіндегі адсорбция Презентация к уроку Плотность вещества, 7 класс
Презентация к уроку Плотность вещества, 7 класс