Содержание
- 2. Нестационарная теплопроводность Температуры: - окружающей среды (жидкости); - поверхности тела (стенки); - в центре тела.
- 3. Дифференциальное уравнение теплопроводности Нестационарная теплопроводность имеет место при нагревании и охлаждении заготовок, пуске и отключении теплоэнергетических
- 4. Охлаждение пластины
- 5. Начальные и граничные условия Рассматриваем охлаждение (нагревание) пластины при: Подставляем избыточную температуру пластины в дифференциальное уравнение
- 6. Решение Решение дифференциального уравнения (2) ищем в виде произведения двух функций, из которых одна является только
- 7. Решение Так как левая часть уравнения (6) является только функцией , а правая – только х,
- 8. Решение Решим (7)
- 9. Решение Решим (8)
- 10. Решение Общее решение: (9)
- 11. Решение Решение (9) подчиним граничному условию (3): (10)
- 12. Решение Подчиним решение (10) граничному условию (4): (11)
- 13. Решение Обозначим тогда Уравнение (11) примет вид: (12) где
- 14. Графическое решение уравнения охлаждения (нагревания) пластины
- 15. Результаты графического решения При то есть функция совпадает с осью абсцисс, то есть: При то есть
- 16. Значения для пластины
- 17. Решение Таким образом, решение уравнения (10) можно представить как множество решений соответствующее каждому значению ………………………………………………………………..
- 18. Решение Решение уравнения можно представить как сумму частных решений: (13) где - число Фурье; - безразмерная
- 19. Решение Коэффициент найдём из начального условия (3): (14) (13) и (14) есть искомое решение задачи.
- 20. Температура При можно ограничится одним членом ряда, тогда
- 21. Решение Пусть тогда
- 22. Решение .
- 23. Температура где
- 24. Температура В размерном виде:
- 25. Температура Температура в центре пластины: Температура на поверхности пластины:
- 26. Температура Средняя температура по толщине пластины:
- 27. Тепловой поток Тепловой поток определяется по закону Фурье:
- 28. Количество теплоты Количество теплоты, отданное пластиной в процессе охлаждения, определяется по формуле: Полное количество теплоты, отданное
- 29. График логарифмический
- 30. . . . . Внутренняя задача ● Частный случай (А): (практически Bi >100): Bi – число
- 31. . . . . А) Внутренняя задача В) Внешняя задача А) В)
- 32. . . . . Внешняя задача ● Частный случай (В): (практически Bi теплопроводность (λ) значительная. Из-за
- 33. . . . . Внешняя задача ● Частный случай (В): (практически Bi теплопроводность (λ) значительная. Из-за
- 34. . . . . Температурное поле в пластине
- 35. Охлаждение бесконечного цилиндра Пусть внутри источник теплоты отсутствует: Пусть Тогда дифференциальное уравнение температурного поля примет вид:
- 36. Охлаждение бесконечного цилиндра Начальные условия: (2) Граничные условия (3) (4)
- 37. Охлаждение бесконечного цилиндра Избыточная температура: Тогда (1)-(4) примет вид: (5) (6) (7) (8)
- 38. Охлаждение бесконечного цилиндра Решение ищем методом Фурье разделенных переменных: Тогда уравнение (5) примет вид (9)
- 39. Охлаждение бесконечного цилиндра Из (9) получим 2 уравнения: (10) (11)
- 40. Охлаждение бесконечного цилиндра решение уравнения (10): решение уравнения (11):
- 41. Охлаждение бесконечного цилиндра - функция Бесселя 1-го рода 0-порядка; - функция Бесселя 2-го рода 0-порядка; При
- 42. Охлаждение бесконечного цилиндра Тогда решение принимает вид: (12)
- 43. Температура Подчинив решение (12) граничным условиям (8) получим характеристическое уравнение для нахождения : Решение уравнения можно
- 44. Температура Для нахождения используем начальные условия (6) (14) (13) и (14) есть искомое решение задачи.
- 45. Температура При начальном равномерном распределении температуры:
- 46. ОХЛАЖДЕНИЕ ШАРА Пусть внутренние источники теплоты отсутствуют, то есть Пусть температура изменяется только в радиальном направлении,
- 47. ОХЛАЖДЕНИЕ ШАРА Начальные условия: Граничные условия:
- 48. ОХЛАЖДЕНИЕ ШАРА Избыточная температура:
- 49. Температура Решение уравнения имеет вид: где - коэффициент, зависящий от начальных условий. Характеристическое уравнение:
- 50. Температура Или:
- 52. Скачать презентацию

















































 Методы и средства измерения частоты, временных интервалов и фазового сдвига
Методы и средства измерения частоты, временных интервалов и фазового сдвига Простые механизмы
Простые механизмы Самостоятельная робота на уроках физики
Самостоятельная робота на уроках физики Imitation of low voltage DC arc
Imitation of low voltage DC arc Оборудование для заземления нейтрали в сетях 6-35 кВ
Оборудование для заземления нейтрали в сетях 6-35 кВ Вес тела. Единицы силы. Связь между силой тяжести и массой тела. Физика. 7 класс
Вес тела. Единицы силы. Связь между силой тяжести и массой тела. Физика. 7 класс Портфолио учителя физики Бушмакиной Е. С.
Портфолио учителя физики Бушмакиной Е. С. Разработка урока по теме Изучение колебаний математического маятника
Разработка урока по теме Изучение колебаний математического маятника Устройство и принцип работы воздухораспределителя 483
Устройство и принцип работы воздухораспределителя 483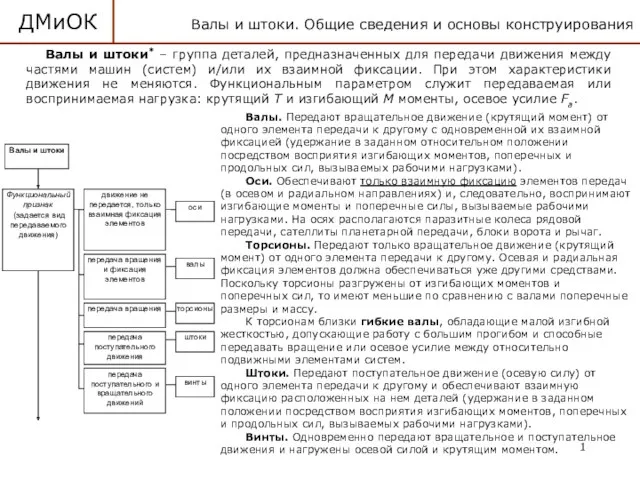 Детали машин и основы конструирования. Валы и штоки. (Лекция 11)
Детали машин и основы конструирования. Валы и штоки. (Лекция 11) Плотность вещества
Плотность вещества Тепловое излучение. Глава 5
Тепловое излучение. Глава 5 Реактивное движение
Реактивное движение Корабельные гироскопические системы. (Тема 2)
Корабельные гироскопические системы. (Тема 2) Температура
Температура Умови плавання тіл
Умови плавання тіл Углекислотные лазеры высокого и низкого давления
Углекислотные лазеры высокого и низкого давления Лекція №5. Закон збереження імпульсу
Лекція №5. Закон збереження імпульсу Взаємодія тіл. Імпульс. Закон збереження імпульсу
Взаємодія тіл. Імпульс. Закон збереження імпульсу Магнитное поле. Действие магнитного поля на движущийся электрический заряд
Магнитное поле. Действие магнитного поля на движущийся электрический заряд Современные приборы измерения температуры
Современные приборы измерения температуры Измерение активного сопротивления обмоток постоянному току
Измерение активного сопротивления обмоток постоянному току Законы отражения
Законы отражения Newton’s Laws of Motion
Newton’s Laws of Motion Технологический процесс проведения опрессовки форсунок судового двигателя
Технологический процесс проведения опрессовки форсунок судового двигателя Гамма-излучение
Гамма-излучение Спектрально-люминесцентные свойства кристаллов стабилизированного диоксида циркония, активированных ионами
Спектрально-люминесцентные свойства кристаллов стабилизированного диоксида циркония, активированных ионами Оптическое явление атмосферы гало
Оптическое явление атмосферы гало