Содержание
- 2. Тема 2. Основные теоремы электростатики План лекции 1. Циркуляция вектора напряжённости. Теорема о циркуляции вектора напряжённости.
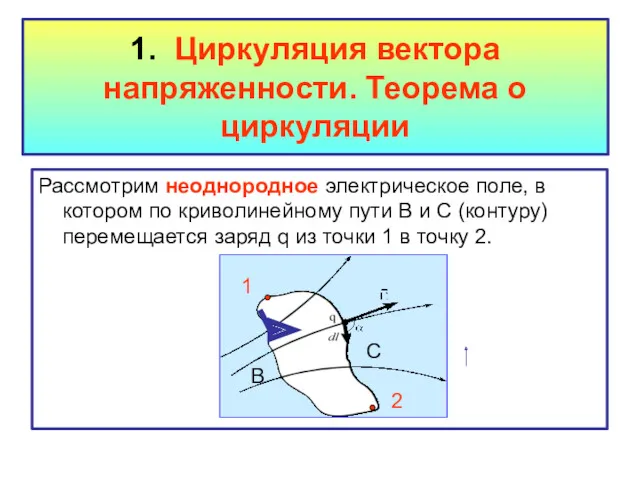
- 3. 1. Циркуляция вектора напряженности. Теорема о циркуляции Рассмотрим неоднородное электрическое поле, в котором по криволинейному пути
- 4. В предыдущей теме показано, что работа сил электростатического поля: - не зависит от формы пути: А1В2
- 5. Представим работу сил как или после сокращения на q: Циркуляцией вектора напряжённости называется интеграл типа
- 6. Циркуляция вектора напряженности: равна работе сил электростатического поля по перемещению единичного заряда вдоль замкнутого контура (физический
- 7. Теорема о циркуляции вектора напряжённости: циркуляция вектора напряжённости электростатического поля по замкнутому контуру равна нулю. Физический
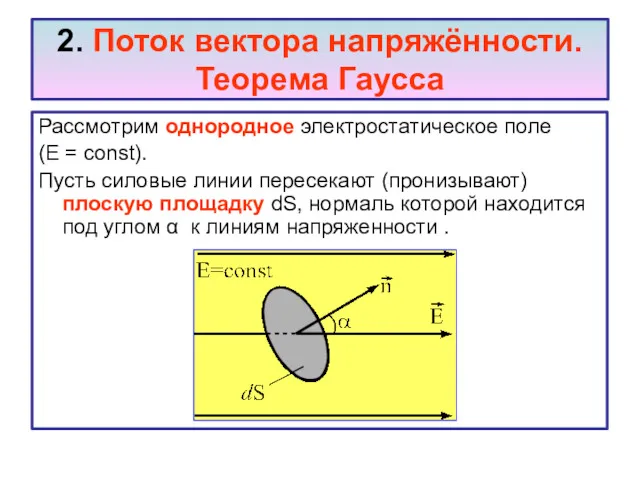
- 8. 2. Поток вектора напряжённости. Теорема Гаусса Рассмотрим однородное электростатическое поле (Е = const). Пусть силовые линии
- 9. Элементарный поток вектора напряжённости определяется выражением: En – проекция вектора на нормаль к площадке dS. Элементарный
- 10. Полный поток вектора определяет число силовых линий, пронизывающих всю плоскую поверхность S (физический смысл). Таким образом,
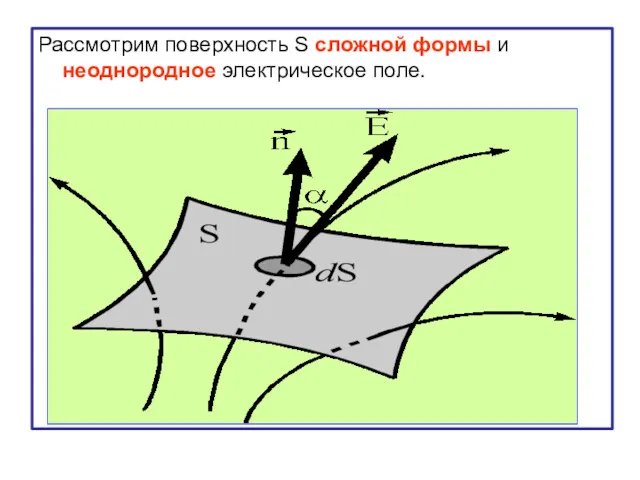
- 11. Рассмотрим поверхность S сложной формы и неоднородное электрическое поле.
- 12. В этом случае поверхность S разбивается на такие маленькие участки dS, в пределах которых поле можно
- 13. Если поверхность S будет замкнутой, то силовые линии неоднородного поля будут входить в поверхность и выходить
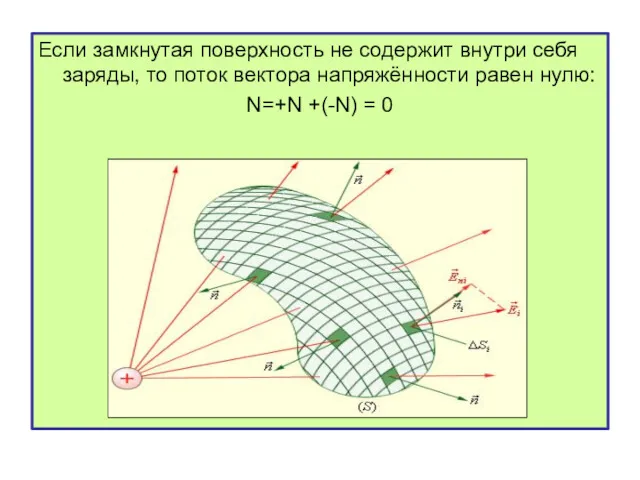
- 14. Если замкнутая поверхность не содержит внутри себя заряды, то поток вектора напряжённости равен нулю: N=+N +(-N)
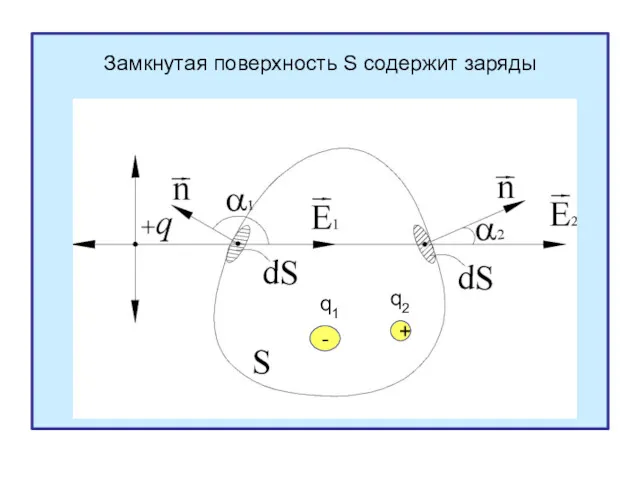
- 15. Замкнутая поверхность S содержит заряды - q1 q2 +
- 16. Теорема о потоке вектора напряжённости (теорема Гаусса) формулируется: поток вектора напряженности электрического поля через произвольную замкнутую
- 17. Физическое содержание теоремы Гаусса: силовые линии электростатического поля начинаются и оканчиваются на неподвижных зарядах; источником электростатического
- 18. 3. Методы расчёта электрических полей Важной прикладной задачей электростатики является расчет электрических полей, имеющихся в различных
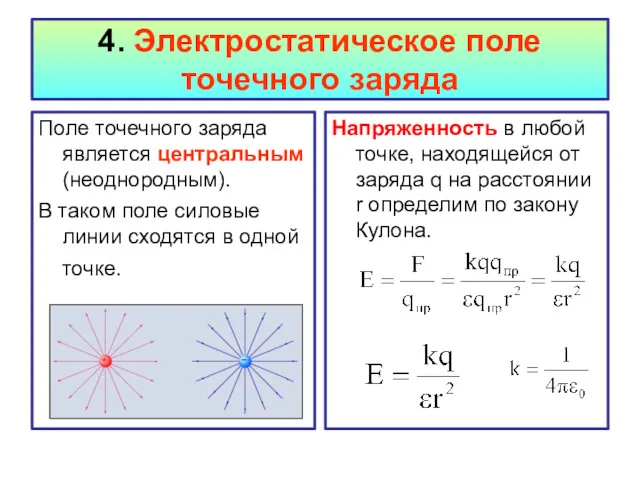
- 19. 4. Электростатическое поле точечного заряда Поле точечного заряда является центральным (неоднородным). В таком поле силовые линии
- 20. Разность потенциалов двух точек поля с потенциалами ϕ1 и ϕ2 определим на основе формулы Проинтегрируем это
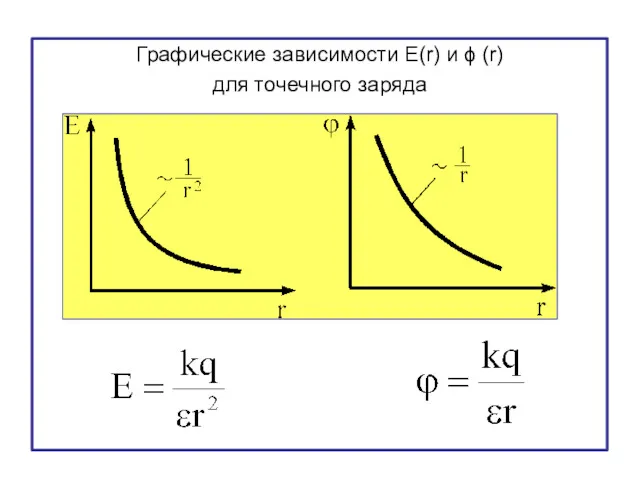
- 21. Графические зависимости E(r) и ϕ (r) для точечного заряда
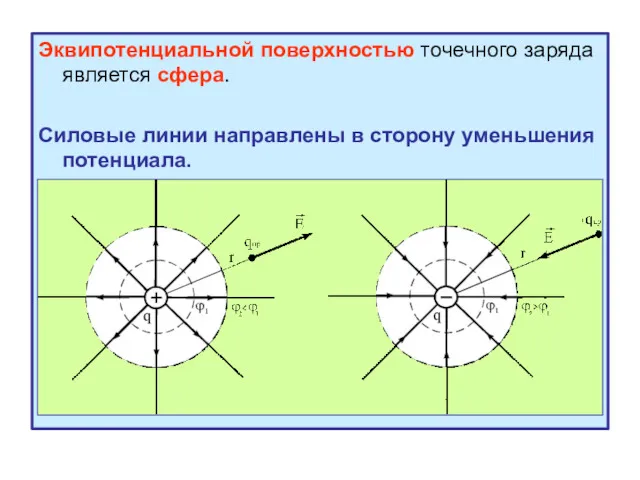
- 22. Эквипотенциальной поверхностью точечного заряда является сфера. Силовые линии направлены в сторону уменьшения потенциала.
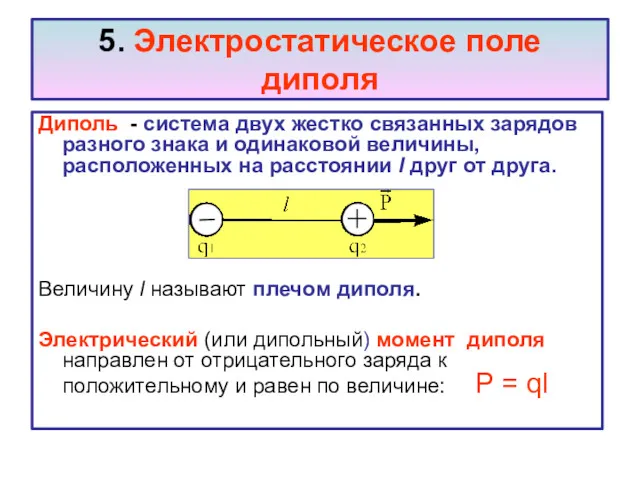
- 23. 5. Электростатическое поле диполя Диполь - система двух жестко связанных зарядов разного знака и одинаковой величины,
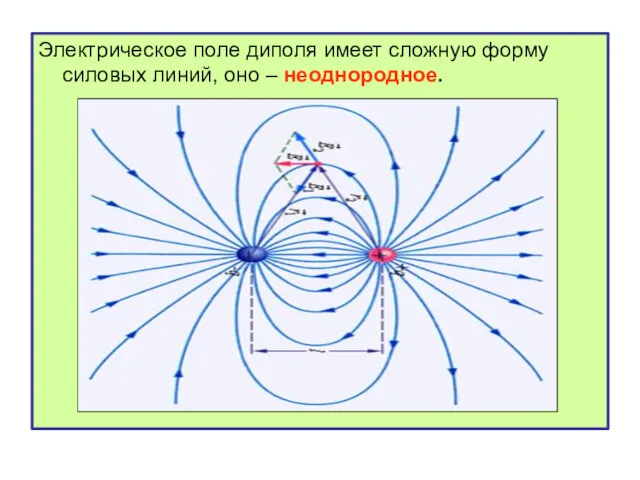
- 24. Электрическое поле диполя имеет сложную форму силовых линий, оно – неоднородное.
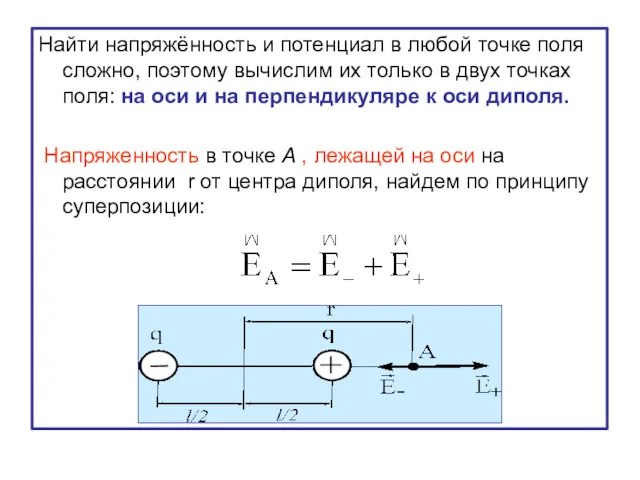
- 25. Найти напряжённость и потенциал в любой точке поля сложно, поэтому вычислим их только в двух точках
- 26. Поскольку векторы и направлены в разные стороны (причем, > ), то суммарная напряженность в скалярной форме
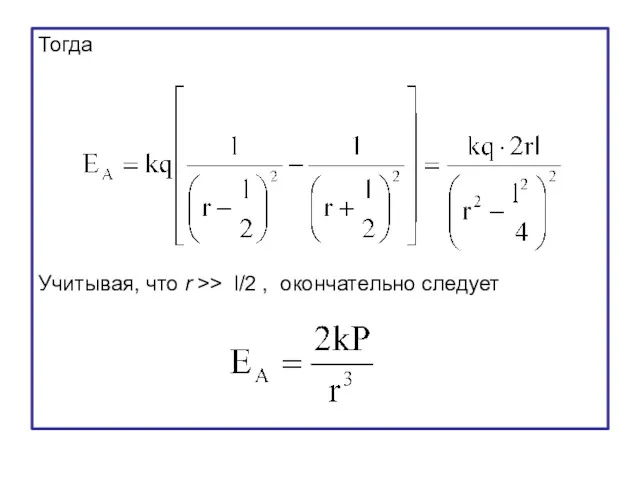
- 27. Тогда Учитывая, что r >> l/2 , окончательно следует
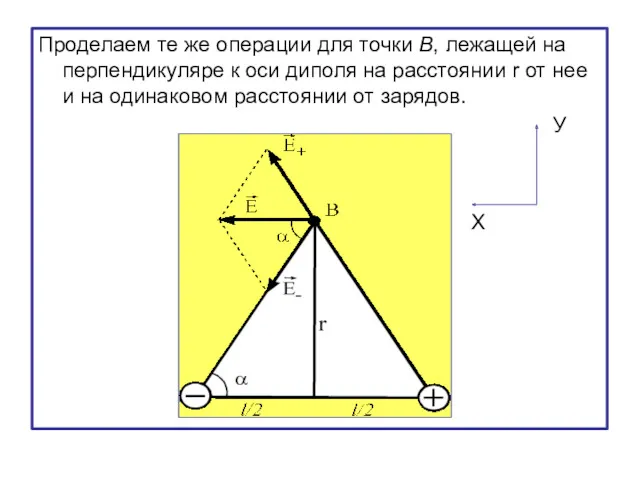
- 28. Проделаем те же операции для точки В, лежащей на перпендикуляре к оси диполя на расстоянии r
- 29. В этом случае Суммарная напряжённость в проекциях на ось У равна нулю. Суммарная напряженность в проекциях
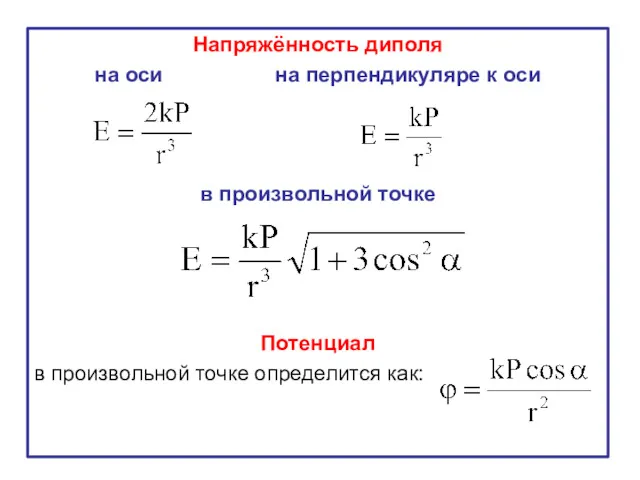
- 30. Напряжённость диполя на оси на перпендикуляре к оси в произвольной точке Потенциал в произвольной точке определится
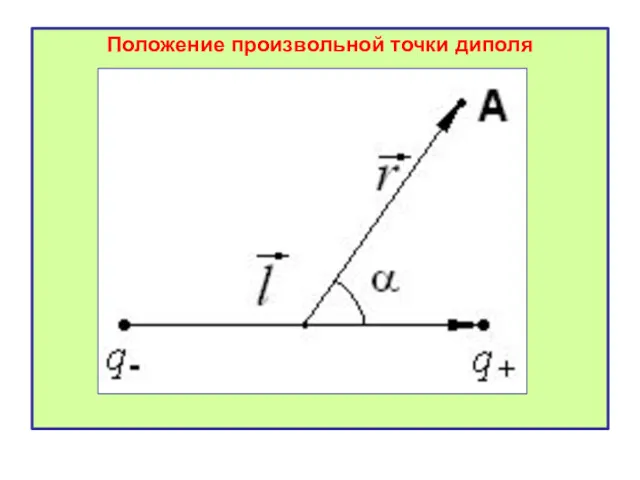
- 31. Положение произвольной точки диполя
- 33. Скачать презентацию















 Информационный материал для стенда в кабинет физики
Информационный материал для стенда в кабинет физики Магнитное поле. Индукция магнитного поля. Закон Био-Савара-Лапласа. Принцип суперпозиции
Магнитное поле. Индукция магнитного поля. Закон Био-Савара-Лапласа. Принцип суперпозиции Как вычислить проекцию?
Как вычислить проекцию? Прості механізми. Момент сили. Важіль. Умови рівноваги важеля
Прості механізми. Момент сили. Важіль. Умови рівноваги важеля Структурные схемы, типовые соединения звеньев. Линейные системы
Структурные схемы, типовые соединения звеньев. Линейные системы Коррозионная стойкость и прочность сварных соединений
Коррозионная стойкость и прочность сварных соединений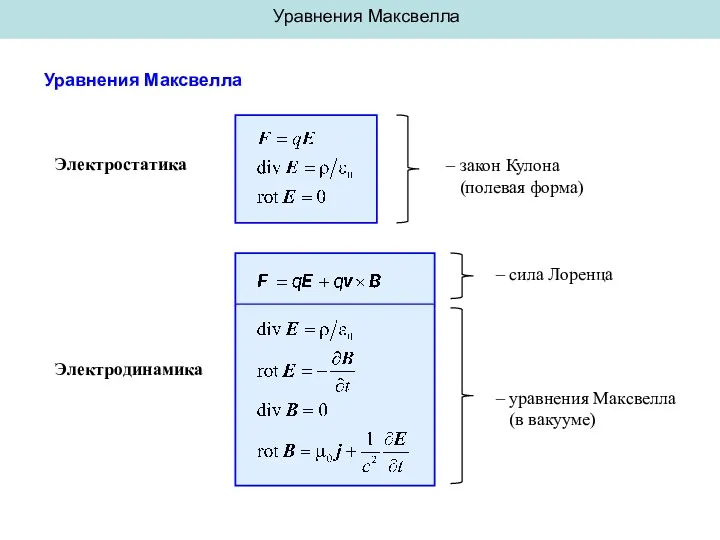 Уравнения Максвелла
Уравнения Максвелла Тепломассообмен. Поперечное обтекание одиночных труб и трубных пучков
Тепломассообмен. Поперечное обтекание одиночных труб и трубных пучков Выполнение судовых работ. Международные правила предупреждения столкновений судов в море
Выполнение судовых работ. Международные правила предупреждения столкновений судов в море Центр тяжести
Центр тяжести Виды излучений. Источники света. Спектры и спектральный анализ. Шкала электромагнитных волн
Виды излучений. Источники света. Спектры и спектральный анализ. Шкала электромагнитных волн Свободные и вынужденные электромагнитные колебания. Колебательный контур. Превращение энергии при электромагнитных колебаниях
Свободные и вынужденные электромагнитные колебания. Колебательный контур. Превращение энергии при электромагнитных колебаниях Источники света. Распространение света. 8 класс
Источники света. Распространение света. 8 класс Технологический процесс технического обслуживания и ремонта системы питания автомобиля ГАЗ- 3307
Технологический процесс технического обслуживания и ремонта системы питания автомобиля ГАЗ- 3307 Тепловые двигатели
Тепловые двигатели Закон Ома для однородного участка цепи в дифференциальной форме
Закон Ома для однородного участка цепи в дифференциальной форме Вакуумдағы электр тогы жөніндегі оқу материалын тө мендегідей жүйелілікпен оқытқан қолайлы болар деп санаймыз
Вакуумдағы электр тогы жөніндегі оқу материалын тө мендегідей жүйелілікпен оқытқан қолайлы болар деп санаймыз Изопроцессы в газах
Изопроцессы в газах Вихревое электрическое поле. Самоиндукция
Вихревое электрическое поле. Самоиндукция Mitsubishi Pajero sport жеңіл автокөлігінің алдыңғы жетекші белдігі
Mitsubishi Pajero sport жеңіл автокөлігінің алдыңғы жетекші белдігі Электроемкость. Конденсаторы
Электроемкость. Конденсаторы 20231003_prezentatsiya
20231003_prezentatsiya Вечный двигатель - воображаемое устройство, способное бесконечно совершать работу без затрат топлива
Вечный двигатель - воображаемое устройство, способное бесконечно совершать работу без затрат топлива Общие теоремы динамики материальной точки
Общие теоремы динамики материальной точки Влияние мобильного телефона на здоровье школьника
Влияние мобильного телефона на здоровье школьника Kappa (κ) Engine
Kappa (κ) Engine Соединения с натягом
Соединения с натягом Спутники
Спутники