Содержание
- 2. Явление синхронизации наблюдается не только в автоколебательных системах с регулярной динамикой, но и в системах, находящихся
- 3. Классический подход к проблеме синхронизации хаотических автоколебаний. Частотно – фазовая синхронизация Классические представления о синхронизации можно
- 4. используя последовательность моментов времени tk, соответствующих пересечению траекторией некоторой секущей плоскости в одном направлении (3) В
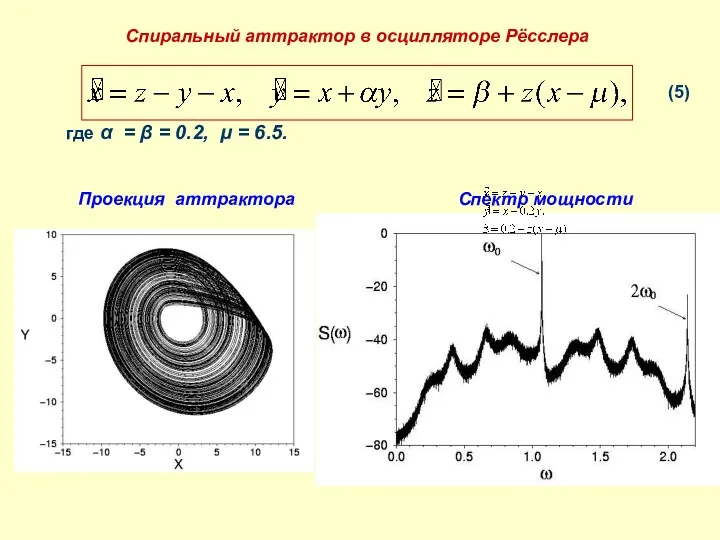
- 5. Спиральный аттрактор в осцилляторе Рёсслера где α = β = 0.2, μ = 6.5. Проекция аттрактора
- 6. Частотно – фазовая синхронизация хаоса означает: Кратность базовых часто взаимодействующих систем nω01 = mω02; Ограниченность разности
- 7. Численное исследование частотно –фазовой синхронизации хаоса в системе Рёсслера с гармоническим внешним воздействием Модель: α =
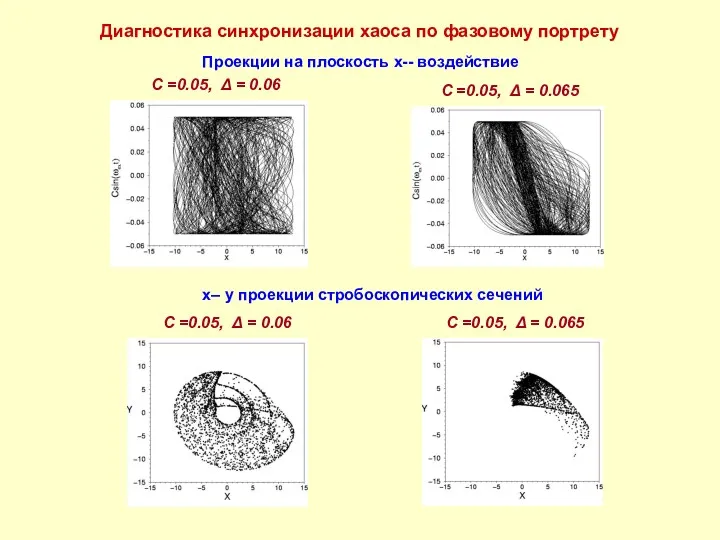
- 8. Диагностика синхронизации хаоса по фазовому портрету Проекции на плоскость x-- воздействие C =0.05, Δ = 0.06
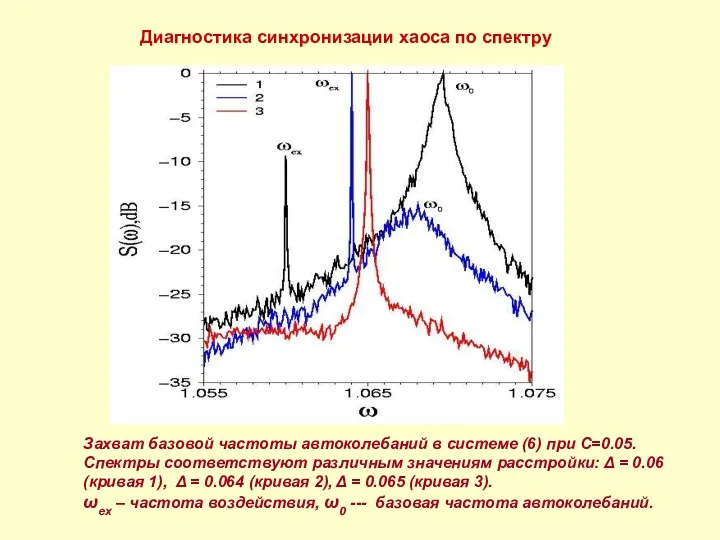
- 9. Диагностика синхронизации хаоса по спектру Захват базовой частоты автоколебаний в системе (6) при C=0.05. Спектры соответствуют
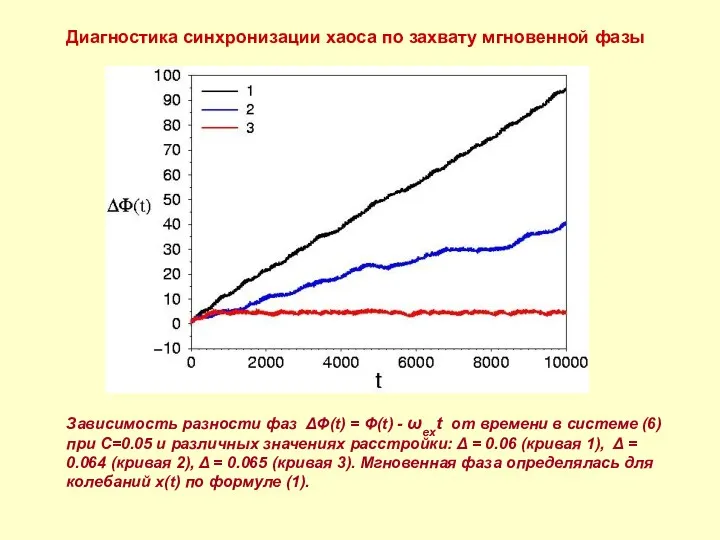
- 10. Диагностика синхронизации хаоса по захвату мгновенной фазы Зависимость разности фаз ΔΦ(t) = Φ(t) - ωext от
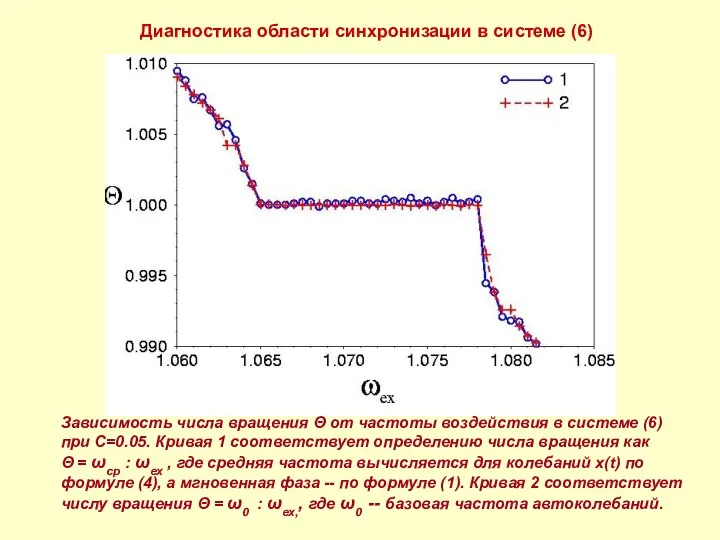
- 11. Диагностика области синхронизации в системе (6) Зависимость числа вращения Θ от частоты воздействия в системе (6)
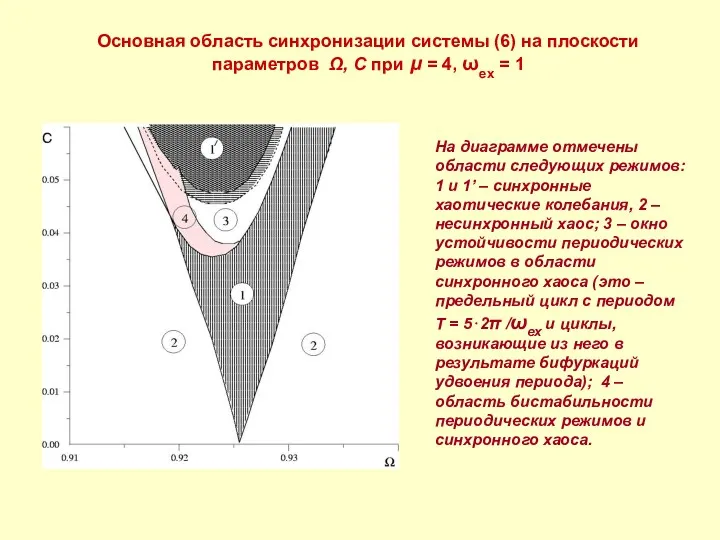
- 12. Основная область синхронизации системы (6) на плоскости параметров Ω, C при μ = 4, ωex =
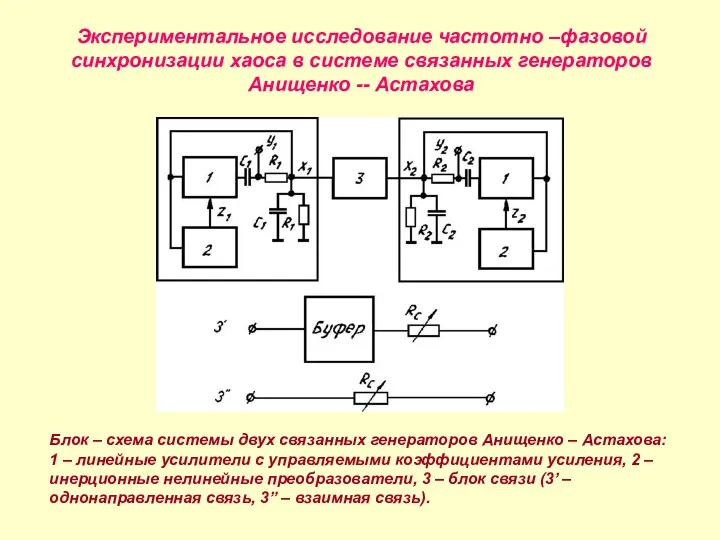
- 13. Экспериментальное исследование частотно –фазовой синхронизации хаоса в системе связанных генераторов Анищенко -- Астахова Блок – схема
- 14. Математическая модель экспериментальной системы (6) где m12 и g12 – параметры, управляющие динамическим режимом парциального генератора;
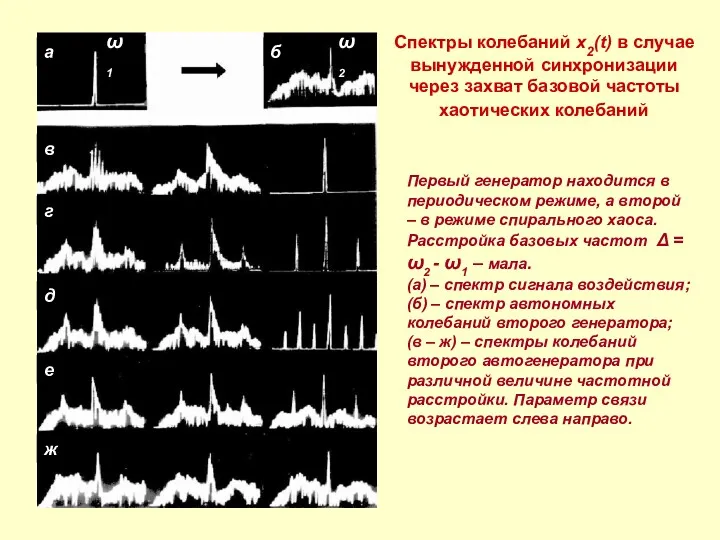
- 15. Спектры колебаний x2(t) в случае вынужденной синхронизации через захват базовой частоты хаотических колебаний Первый генератор находится
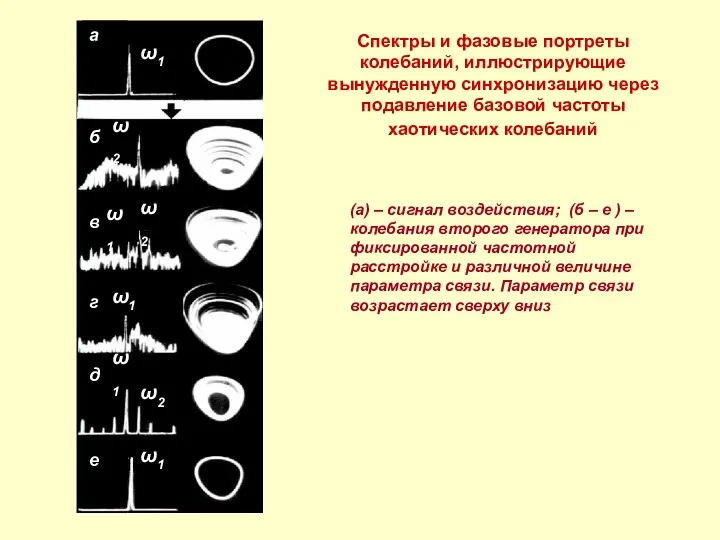
- 16. Спектры и фазовые портреты колебаний, иллюстрирующие вынужденную синхронизацию через подавление базовой частоты хаотических колебаний (а) –
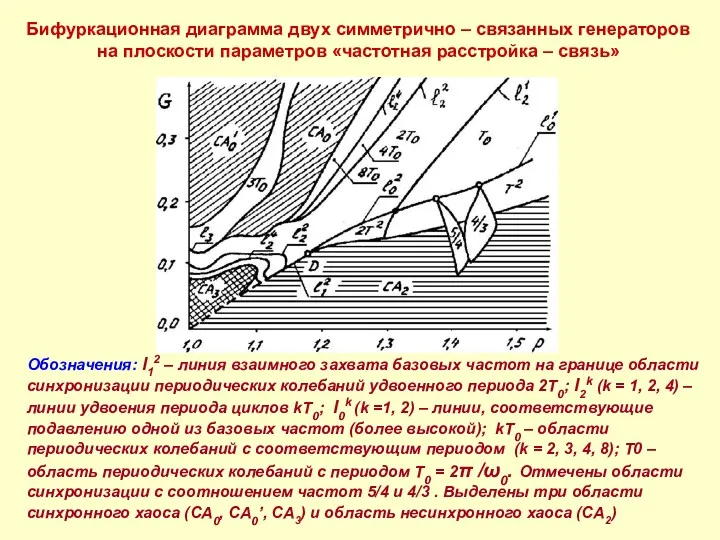
- 17. Бифуркационная диаграмма двух симметрично – связанных генераторов на плоскости параметров «частотная расстройка – связь» Обозначения: l12
- 18. Полная синхронизация взаимодействующих хаотических систем При взаимодействии (в том числе однонаправленном) двух совершенно идентичных хаотических систем
- 19. Если предельное множество, принадлежащее U, притягивает фазовые траектории не только из U, но и из некоторой
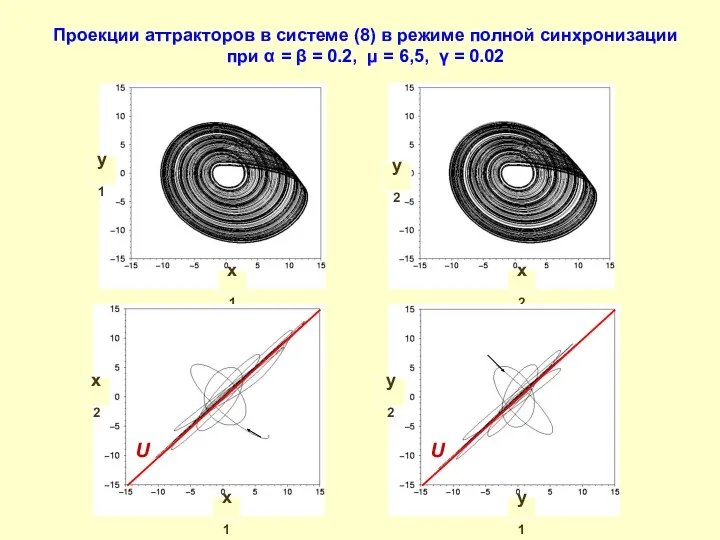
- 20. Проекции аттракторов в системе (8) в режиме полной синхронизации при α = β = 0.2, μ
- 21. Замечания. Полная синхронизация может наблюдаться не только в режиме спирального хаоса, но и в более сложных
- 23. Скачать презентацию









 Основной закон электростатики - закон Кулона
Основной закон электростатики - закон Кулона Анализ физико-химического состава почвы пришкольного участка
Анализ физико-химического состава почвы пришкольного участка Плавление и кристаллизация
Плавление и кристаллизация Внутренняя энергия. Первый закон термодинамики
Внутренняя энергия. Первый закон термодинамики Назначение, устройство и работа ГРМ легкового автомобиля на примере ВАЗ
Назначение, устройство и работа ГРМ легкового автомобиля на примере ВАЗ Жарық толқындарының интерференциясы
Жарық толқындарының интерференциясы Техническое обслуживание и текущий ремонт ходовой части автомобиля
Техническое обслуживание и текущий ремонт ходовой части автомобиля Цилиндрические зубчатые передачи. Кинематический расчет привода
Цилиндрические зубчатые передачи. Кинематический расчет привода Сопротивление материалов: деформация, напряжение
Сопротивление материалов: деформация, напряжение презентация Сообщающиеся сосуды
презентация Сообщающиеся сосуды Элементы физической кинетики
Элементы физической кинетики Механизм құрылымы
Механизм құрылымы Потенциалы Лиенара-Вихерта. Поле точечного заряда
Потенциалы Лиенара-Вихерта. Поле точечного заряда Динамика твердого тела
Динамика твердого тела Равновесные и неравновесные носители зарядов
Равновесные и неравновесные носители зарядов Однофазная цепь с последовательным соединением электроприемников
Однофазная цепь с последовательным соединением электроприемников Вечный двигатель
Вечный двигатель Прямолінійний рівноприскорений рух
Прямолінійний рівноприскорений рух Звукові хвилі. Інфразвук і ультразвук
Звукові хвилі. Інфразвук і ультразвук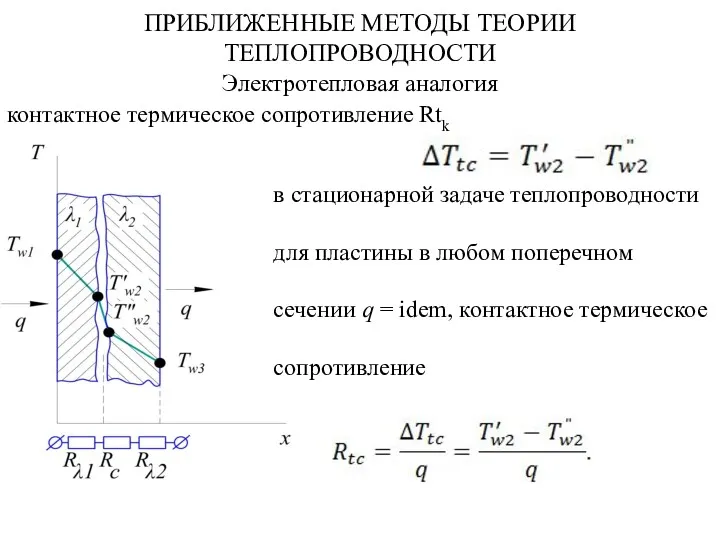 Приближенные методы теории теплопроводности. Электротепловая аналогия
Приближенные методы теории теплопроводности. Электротепловая аналогия Механические колебания. Кинематика и динамика колебательного движения
Механические колебания. Кинематика и динамика колебательного движения Энергия. Виды энергии. Презентация
Энергия. Виды энергии. Презентация Электрическое поле и его напряженность. Принцип суперпозиции полей точечных зарядов
Электрическое поле и его напряженность. Принцип суперпозиции полей точечных зарядов Диапазон частот. Радиодиапазон
Диапазон частот. Радиодиапазон Физика в професії кухаря
Физика в професії кухаря Физика. Аристотель
Физика. Аристотель Как люди научились считать время
Как люди научились считать время Презентация по физики в 7 классе. Тема Скорость. Единицы скорости
Презентация по физики в 7 классе. Тема Скорость. Единицы скорости