Содержание
- 2. Расчеты на прочность и жесткость при косом изгибе Косым изгибом называется такой случай изгиба бруса, при
- 3. Y X Z Y X Z Силовые плоскости Прямой плоский изгиб Косой плоский изгиб Рис.1 Рис.2
- 4. Стропила Обрешетины кровли Кровельный материал Косой изгиб возникает, например, в обрешетинах кровли от веса самой кровли,
- 5. Косой пространственный изгиб F1 F2 Косой изгиб бывает двух видов: 1) пространственный косой изгиб, когда действующая
- 6. 2) плоский косой изгиб, который возникает в случаях, когда вся действующая на брус нагрузка лежит в
- 7. Внутренние усилия при косом изгибе. Рассмотрим брус, на свободный конец которого действует сила F, линия действия
- 8. Mx My растяжение сжатие Fx Fy Момент Мх (Му) положителен, если он вызывает в точках первой
- 9. Fx F α Fy Y Z Силовая плоскость Mu В случае плоского косого изгиба удобно пользовать-ся
- 10. Fx F α Fy Y X Z Mu Силовая линия Силовая плоскость Mu Назовем силовой линией
- 11. Mu Силовая линия (8.2) Угол ά наклона силовой ли- нии к оси Y найдем из фор-
- 12. Напряжения при косом изгибе Напряжения во всех случаях сложного сопротивления , в том чис-ле и при
- 13. σzMy σzMx В формуле (8.3) x u y– это координа-ты точки, в которой определяется напряжениe. При
- 14. Qy Qx 2. Касательные напряжения. При определении касательных на-пряжений необходимо определять их геометрическую сумму, так как
- 15. Y X Z X Z Исследование напряженного состояния в точке при косом изгибе. Рассмотрим кон-сольную балку
- 16. Y X Z Вырежем вокруг этой точки элементарный параллелепипед. Изобразим этот параллелепипед в увеличенном виде, нагрузим
- 17. 1). Нормальные напряжения на верх-ней и передней гранях параллелепи-педа отсутствуют в силу гипотезы о ненадавливании продольных
- 18. Таким образом, у элементарного параллелепипеда нет свободных от напряжений площадок, то есть имеет место пространственное напряжен-ное
- 19. Опасные точки сечения. Нейтральная линия сечения. Из формул (8.3) и (8.4) следует, что прежде, чем вос-пользоваться
- 20. Предположим, что точка N ( xN ,yN) лежит на нейтральной линии . Тогда Н.л. φ yN
- 21. Выясним, какими свойствами обладает нейтральная линия при косом изгибе. 1). Найдем напряжения в центре тяжести сечения
- 22. 3).Сравним выражения (8.2) и (8.5). (8.5) (8.2) (8.6) С.л. ά c Нейтральная и силовая линии в
- 23. 4) Получим зависимость величины нормальных напряжений в точке сечения от положения этой точки относительно нейтраль-ной линии.
- 24. Н.л. φ M x y c K T φ L p B Из чертежа следует =MT+TB=MT+KL;
- 25. Н.л. φ M c p Из формулы (8.8) сле-дует, что чем больше р, то есть чем
- 26. Н.л. φ M c p . σрmax σсmax Из формулы (8.8) также следует, что напряжения линейно
- 27. В сечениях простой формы (прямоугольник, двутавр, швеллер и т.п.) опасными точками сечения будут угловые точки. Н.л.
- 28. Y X Расчет круглого сечения. Из (8.8) pmax Из (8.1) Выпишем формулу (8.6) Для круглого сечения
- 29. Так как косой изгиб представляет собой сочетание двух прямых изгибов, то перемещения при косом изгибе определяются
- 30. v u f ϒ Для этого сначала все нагрузки раскладываются на составляющие, дей- и направление прогиба
- 32. Скачать презентацию
 Презентация Звуковые волны
Презентация Звуковые волны Динамометр. Механический динамометр
Динамометр. Механический динамометр Теплоемкость идеального газа при изопроцессах. Лекция 12
Теплоемкость идеального газа при изопроцессах. Лекция 12 Сила тока
Сила тока Лестница Иакова- Аппарат для производства электрической дуги
Лестница Иакова- Аппарат для производства электрической дуги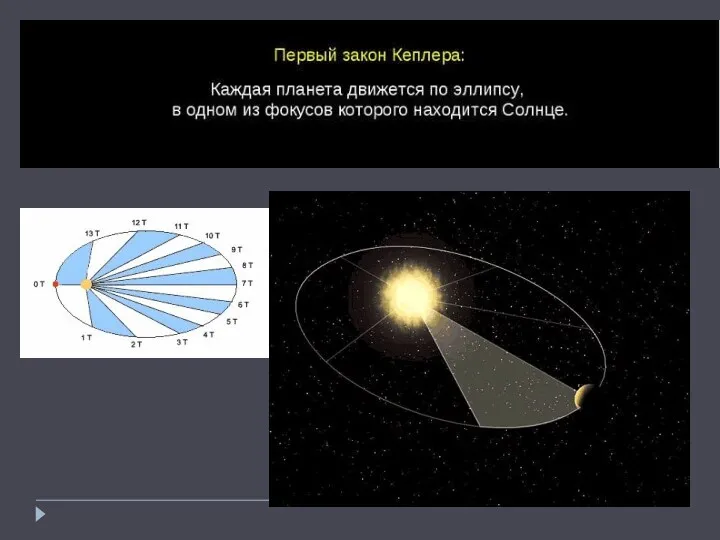 Первый закон Кеплера
Первый закон Кеплера Свойства кристаллов
Свойства кристаллов Источники света
Источники света Презентация к уроку Колебания
Презентация к уроку Колебания Физические основы механики
Физические основы механики Презентация к уроку физики в 8 классе Проводники и диэлектрики
Презентация к уроку физики в 8 классе Проводники и диэлектрики Характеристики двигателей. Тема 10
Характеристики двигателей. Тема 10 Ядерная и термоядерная энергетика. Часть 2
Ядерная и термоядерная энергетика. Часть 2 Традиційна енергетика. Централізовані системи електропостачання
Традиційна енергетика. Централізовані системи електропостачання Квантовая физика. Тема № 5
Квантовая физика. Тема № 5 Источники света. Распространение света. Отражение света. 8 класс
Источники света. Распространение света. Отражение света. 8 класс Устройство и ремонт электропоездов
Устройство и ремонт электропоездов Учебные презентации по физике по темам Электромагнитные волны и Строение атома
Учебные презентации по физике по темам Электромагнитные волны и Строение атома Урок физики 8 класс Испарение и конденсация
Урок физики 8 класс Испарение и конденсация Розв’язування задач за темою Рух тіла під дією кількох сил
Розв’язування задач за темою Рух тіла під дією кількох сил Ударно-тяговые приборы
Ударно-тяговые приборы Мотивация как компонент учебной деятельности. Методы формирования учебной мотивации на уроках физики
Мотивация как компонент учебной деятельности. Методы формирования учебной мотивации на уроках физики Итоговый урок, физика 8 класс
Итоговый урок, физика 8 класс Курс Атомные реакторы и ядерная энергетика. Лекция 3. Ядерная энергетика. Настоящее и будущее
Курс Атомные реакторы и ядерная энергетика. Лекция 3. Ядерная энергетика. Настоящее и будущее Атом водорода в квантовой механике
Атом водорода в квантовой механике Давление твёрдого тела. 7 кл.
Давление твёрдого тела. 7 кл. Ионизирующее излучение
Ионизирующее излучение Діелектрики в електричному полі. Поляризація діелектриків. Діелектрична проникність речовини
Діелектрики в електричному полі. Поляризація діелектриків. Діелектрична проникність речовини