Тепломассообмен. Теория подобия физических явлений. Числа подобия. Уравнения подобия презентация

Условия подобия
процессов конвективного теплообмена
Если систему дифференциальных уравнений и граничные
условия привести к безразмерному виду, то число влияющих
факторов формально сократится, например число (критерий)
Рейнольдса: соотношение сил инерции и вязкости.
Для нахождения явного вида зависимостей (9) нужны опытные
данные. Чтобы результаты опытов на модели можно было
перенести на натуру, необходимо, по условию подобия
процессов на модели и натуре, выдержать равенство
чисел подобия:
.

Условия подобия физических явлений
Если модель изготовлена в масштабе = 1/10, то для
одной и той же жидкости на модели и натуре, для соблюдения
условий подобия необходимо, чтобы отношение скоростей
было = 10, что не всегда можно обеспечить.
Поэтому иногда моделируют процессы на других жидкостях
= 1/10. В теорию подобия внесли большой вклад
Гухман А.А., Кирпичев М.В., Петухов В.С., Михеев М.А. и др.
Приведем систему дифференциальных уравнений и условия
однозначности к безразмерному виду одним из способов -
методом масштабных преобразований.
Получатся безразмерные величины:

Безразмерное дифференциальное уравнение теплоотдачи
Выразим размерные величины через безразмерные и
масштабы отнесения, выбранные из условий однозначности,
подставим их в дифференциальные уравнения
и граничные условия. Тогда дифференциальное уравнение
теплоотдачи примет вид:
После сокращения на и переноса всех
размерных величин в левую сторону получим: (1)
где - число Нуссельта (соотношение конвективной
теплоотдачи вне пограничного слоя и теплопроводности внутри.

Приведение к безразмерному виду дифференциального уравнения энергии
Дифференциальное уравнение энергии для стационарного
режима имеет вид:
(2)
Выразим все размерные величины через безразмерные и
масштабы отнесения:
Тогда дифференциальное уравнение энергии:
(3)

Безразмерное
дифференциальное уравнение энергии
Умножим обе части уравнения (3) на
После сокращений получим безразмерное дифференциальное
уравнение энергии Фурье-Кирхгофа (теплопроводности в
жидкости): . (4)
Здесь число (критерий) Пекле.

Приведение к безразмерному виду уравнения движения
Дифференциальное уравнение движения Навье-Стокса
в проекции на ось х для стационарного режима:
(5)
Умножим обе части уравнения на и вынесем из него
только размерные величины:

Числа подобия
Рейнольдса, Грасгофа, Эйлера
После сокращений имеем: (6)
В левой части - число (критерий) Рейнольдса
(соотношение сил инерции и вязкости). Умножим первый
член правой части
уравнения (6) на:
где число (критерий) Грасгофа – соотношение
подъемных и вязкостных сил.
Второй член правой части равенства (6) умножим на:
где число (критерий) Эйлера – соотношение сил
давления и инерции.

Безразмерное дифференциальное уравнение сплошности (неразрывности)
Тогда безразмерное дифференциальное уравнение движения
Навье-Стокса в проекции на ось х для стационарного режима:
(7)
Проекции уравнения Навье-Стокса на оси y и z не дадут
новых чисел подобия, поэтому их не рассматриваем.
Дифференциальное уравнение сплошности (неразрывности)
или
Так как , то безразмерное дифференциальное
уравнение
сплошности: или (8)

Безразмерные система уравнений
и граничные условия
Безразмерная система дифференциальных уравнений
конвективного теплообмена:
(9)
Граничные условия I рода:
(10)

Определяемые и определяющие
числа подобия
Преобразуем число Пекле
следующим образом:
где число (критерий) Прандтля – соотношение полей
скоростей и температур.
Из безразмерной системы уравнений и граничных условий
можно выявить три вида величин:
● независимые переменные -
● постоянные величины -
● зависимые переменные -
Определяемые числа подобия
Определяющие числа подобия

Общий вид решений конвективной теплоотдачи в безразмерном виде
Каждый определяемый критерий подобия является функцией
определяющих:
(11)
В безразмерных зависимостях (11) шесть влияющих факторов,
по сравнению с двенадцатью - в размерных уравнениях (9)
для (см. Тепломассообмен 10).

Виды подобий
Подобными называются явления, которые имеют одинаковую
физическую природу и описываются одинаковыми по форме
и по содержанию уравнениями.
Бывают следующие виды подобия:
● геометрическое – подобие геометрических фигур;
● тепловое – подобие тепловых потоков и температурных полей;
● кинематическое – подобие движений жидкостей;
● динамическое – подобие сил, вызывающих подобные
движения.
Основные понятия о теории подобия можно получить из трех
теорем подобия.
I теорема – в подобных явлениях
одноименные числа подобия равны:

II и III теоремы
подобия физических явлений
II теорема – решение дифференциального уравнения
(системы уравнений) можно представить в виде функции
от чисел подобия, полученных из этого уравнения:
IIIтеорема – подобны те явления, условия однозначности
которых подобны, а числа подобия, составленные из этих
условий однозначности, равны.
Условия однозначности подобны, если в сходственных точках
в сходственные моменты времени отношение одноименных
величин есть величины постоянные, называемые константами
подобия. Одноименные величины – это величины, имеющие
одинаковый физический смысл и размерности.

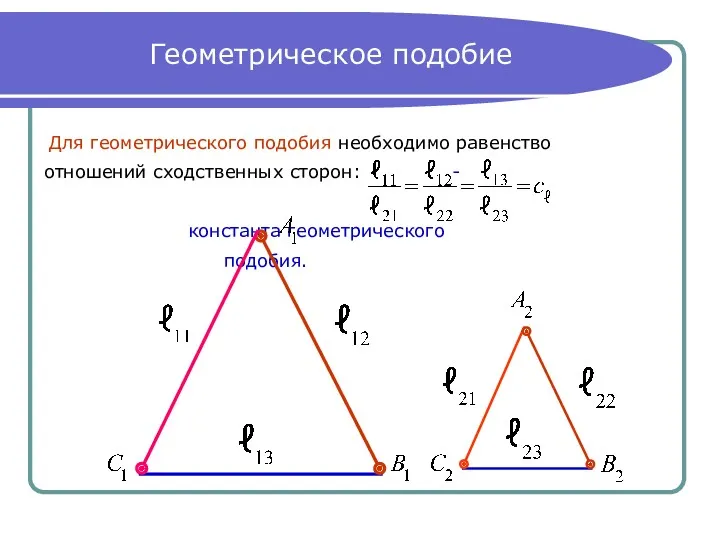
Геометрическое подобие
Для геометрического подобия необходимо равенство
отношений сходственных сторон: -
константа геометрического
подобия.