Содержание
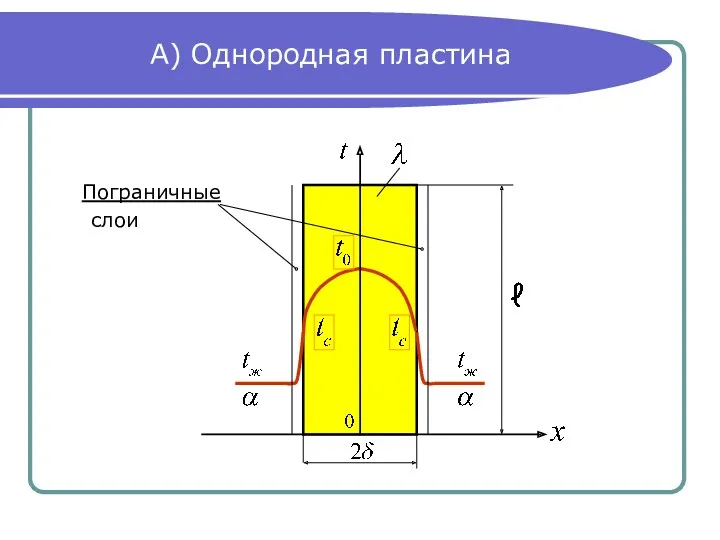
- 2. А) Однородная пластина Пограничные слои
- 3. Дифференциальное уравнение теплопроводности При бесконечная пластина. В стационарном процессе: Найти: Дифференциальное уравнение теплопроводности: (1) Для стационарного
- 4. Граничные условия Условия теплоотдачи одинаковы с обеих сторон пластины, поэтому температурное поле симметричное, а тепловыделения в
- 5. Константы интегрирования Константы интегрирования находятся из граничных условий (4) и уравнения (5) при: , (7) .
- 6. Тепловой поток и температуры Подставим константы интегрирования (7) и (12) в (6): (13) уравнение параболы. Тепловой
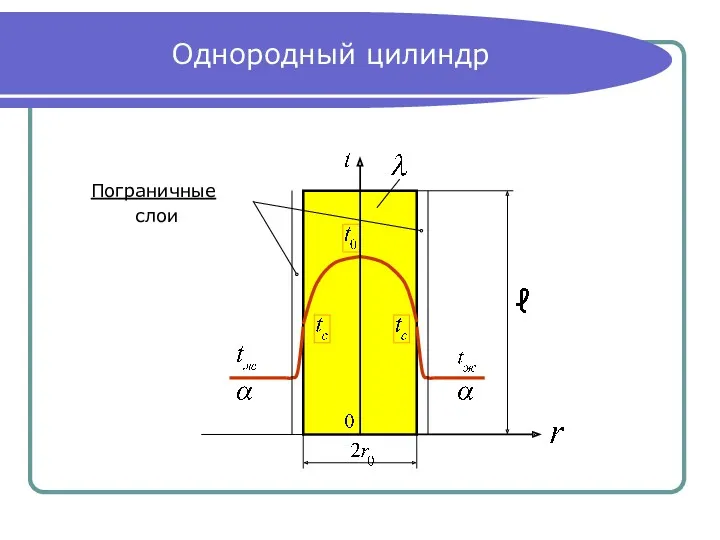
- 7. Однородный цилиндр Пограничные слои
- 8. Дифференциальное уравнение теплопроводности для цилиндра Для бесконечного цилиндрического стержня . При стационарном режиме Найти Условия теплоотдачи
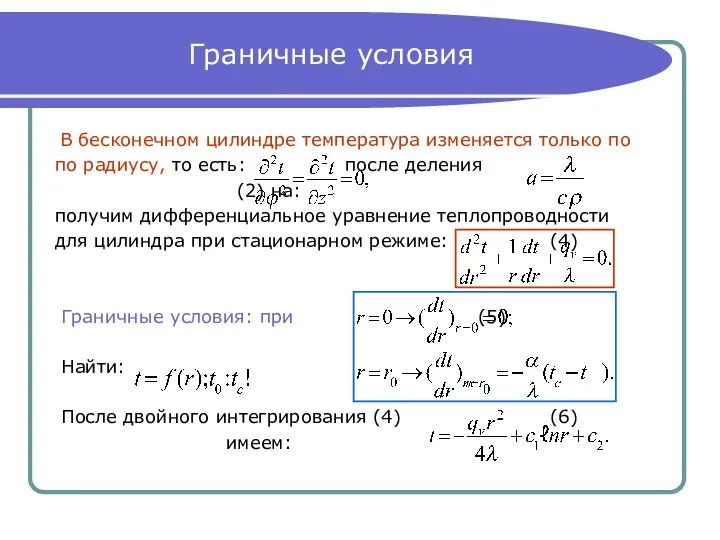
- 9. Граничные условия В бесконечном цилиндре температура изменяется только по по радиусу, то есть: после деления (2)
- 10. Конвективная теплоотдача от цилиндра к жидкости Определив константы интегрирования и подставив их в (6), имеем: (7)
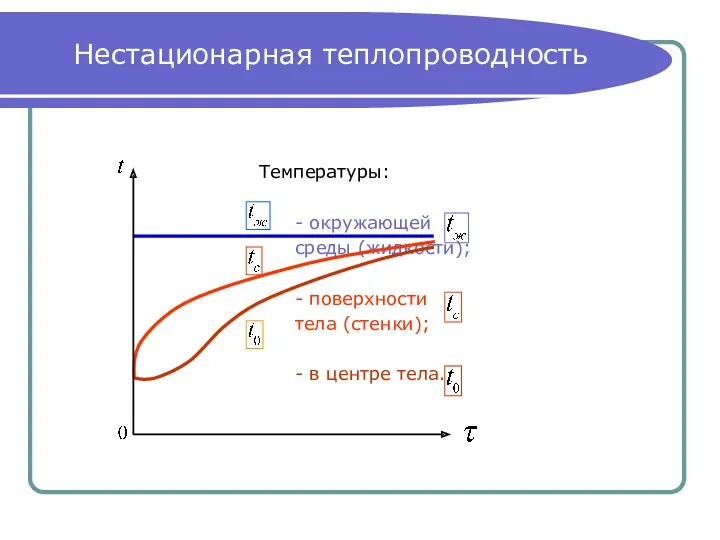
- 11. Нестационарная теплопроводность Температуры: - окружающей среды (жидкости); - поверхности тела (стенки); - в центре тела.
- 12. Дифференциальное уравнение теплопроводности Нестационарная теплопроводность имеет место при нагревании и охлаждении заготовок, пуске и отключении теплоэнергетических
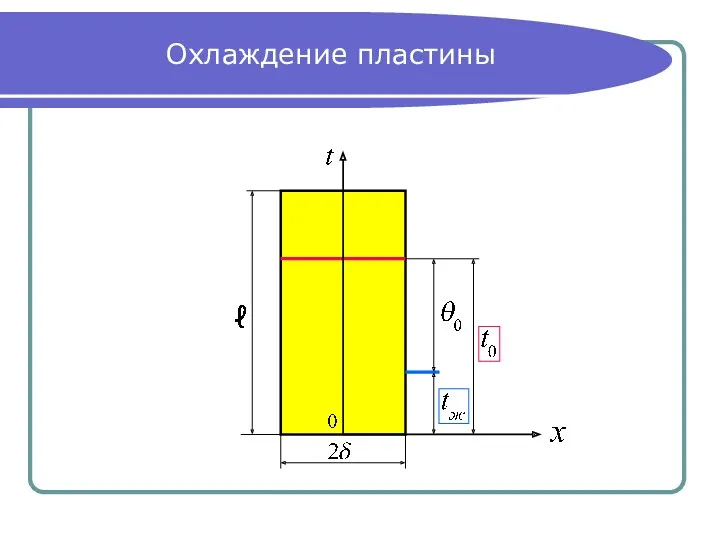
- 13. Охлаждение пластины
- 14. Начальные и граничные условия Рассматриваем охлаждение (нагревание) пластины при: Подставляем избыточную температуру пластины в дифференциальное уравнение
- 15. Разделение переменных Решение дифференциального уравнения (2) ищем в виде: произведения двух функций, из которых одна является
- 16. Решение в общем виде то есть: (7) (8) Получилась система дифференциальных уравнений (7) и (8), которой
- 17. Константы интегрирования Так как то или: При: а при Таким образом, решение надо отбросить, как не
- 18. Аналитическое решение то есть (11) После сокращения на или: Здесь число (критерий) Био – соотношение конвективной
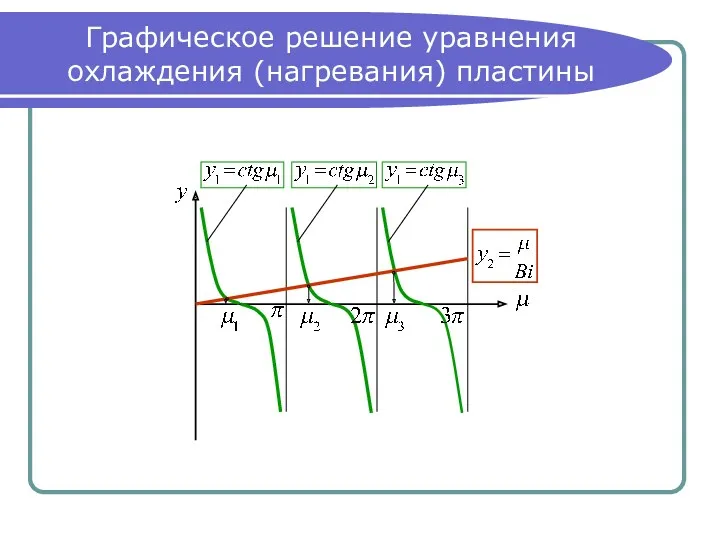
- 19. Графическое решение уравнения охлаждения (нагревания) пластины
- 20. Результаты графического решения При то есть функция совпадает с осью абсцисс, то есть: При то есть
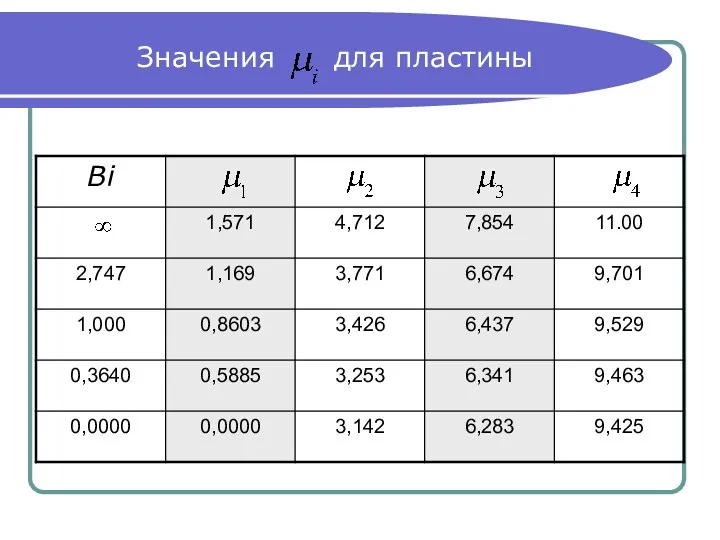
- 21. Значения для пластины
- 22. Условия на оси пластины В безразмерном виде: здесь число Fo (критерий) Фурье – безразмерное время. Для
- 23. Условия на поверхности пластины На поверхности пластины: Введем обозначение тогда: (16) Функции табулированы и могут быть
- 24. Графические решения На оси пластины: (18) На поверхности пластины: (19) Точные графики для оси пластины (Х
- 26. Скачать презентацию
















 Физика в картинках
Физика в картинках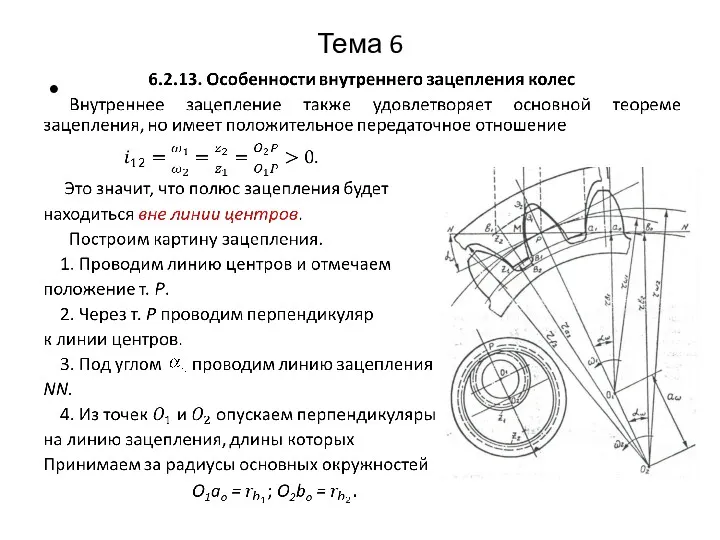 Особенности внутреннего зацепления колес
Особенности внутреннего зацепления колес Давление. Решение задач
Давление. Решение задач Фотоны
Фотоны Гидравлический подъемник. Выбор насоса
Гидравлический подъемник. Выбор насоса Прямолинейное равноускоренное движение. Ускорение
Прямолинейное равноускоренное движение. Ускорение Физические методы измерений. Виды и методы измерений. (Лекция 1)
Физические методы измерений. Виды и методы измерений. (Лекция 1) Гидростатика. Поверхностные явления. Гидромеханика идеальной и вязкой жидкости. Практическое занятие 5
Гидростатика. Поверхностные явления. Гидромеханика идеальной и вязкой жидкости. Практическое занятие 5 X-radiation
X-radiation Гироскопические приборы и устройства
Гироскопические приборы и устройства Электричество и магнетизм
Электричество и магнетизм Сила трения – сила, возникающая при движении одного тела по поверхности другого
Сила трения – сила, возникающая при движении одного тела по поверхности другого Закон Ома для полной цепи
Закон Ома для полной цепи Лекционно-зачетная система обучения физики в старших классах
Лекционно-зачетная система обучения физики в старших классах Двигатель внутреннего сгорания
Двигатель внутреннего сгорания Сила трения
Сила трения Подготовка к ЕГЭ Законы сохранения в механике
Подготовка к ЕГЭ Законы сохранения в механике Методи та системи неруйнівного контролю
Методи та системи неруйнівного контролю Урок по физике 7 класс Мощность
Урок по физике 7 класс Мощность Сила упругости. Закон Гука
Сила упругости. Закон Гука презентация импульс тела закон сохранения импульса
презентация импульс тела закон сохранения импульса Неоднородное одномерное уравнение теплопроводности
Неоднородное одномерное уравнение теплопроводности Зонная модель электронной проводимости металлов
Зонная модель электронной проводимости металлов Презентация по теме Кристаллы и аморфные тела
Презентация по теме Кристаллы и аморфные тела Електродвигун
Електродвигун Классификация и свойства углеродных наноматериалов
Классификация и свойства углеродных наноматериалов Найбільші кораблі
Найбільші кораблі Динамика. Основные понятия
Динамика. Основные понятия