Содержание
- 2. § 4. Нестационарная теплопроводность Процесс теплопроводности в неограниченной пластине описывается уравнением: , – одномерное дифференциальное уравнение
- 3. Для решения дифференциального уравнения воспользуемся методом разделения переменных: T (x, t) = Ф (x) ⋅ П
- 4. Принимаем допущения: 1) считаем, что нагрев (или охлаждение) пластины происходит из-за конвективной теплоотдачи от окружающей среды
- 5. Решение принимает вид: . Краевые условия: Т (x, 0) = TН , . Введем новую переменную
- 6. Краевые условия: ϑ (x, 0) = T0 – TН = ϑН , . Знак в правой
- 7. Подставим решение в граничное условие, например, при x=−δ: ⇒ ⇒ . Обозначим произведение k ⋅ δ
- 8. Жан Батист Био (1774–1862) – французский физик, геодезист и астроном. Его первые работы были посвящены исследованию
- 9. Имеем трансцендентное характеристическое уравнение, которое можно решить графически: . График левой части уравнения представляет собой котангенсоиду,
- 10. Характеристическое уравнение имеет бесчисленное множество корней. В связи с линейностью дифференциального уравнения теплопроводности его общее решение
- 11. Умножим обе части равенства на и проинтегрируем по х в пределах толщины пластины. Меняя порядок интегрирования
- 12. Учитывая, что , получим: . Учтем также, что и sin2x = 2⋅sinx⋅cosx. Тогда .
- 13. Итак, получаем , и решение принимает окончательный вид: , где – безразмерная координата. Таким образом, безразмерная
- 14. Рассмотрим, к чему сводится полученное решение при Bi → 0. При этом угловой коэффициент 1/Bi прямой
- 15. Решение для рассматриваемого случая сводится к следующему: . Определим конкретный вид связи между μ1 и Bi.
- 16. Рассмотрим нестационарную теплопроводность при граничных условиях I рода для неограниченной пластины. Считаем, что на границах пластины
- 17. Считаем, что TW не изменяется: Характеристическое уравнение при Bi→ ∞ принимает вид ctgμn = 0, то
- 18. Выражение для безразмерной избыточной температуры (решение задачи нестационарной теплопроводности при граничных условиях III рода, см. слайд
- 19. В переходных процессах нестационарной теплопроводности, когда температура в каждой точке тела изменяется от одного установившегося значения
- 20. Ряд решения задачи нестационарной теплопроводности из § 17 быстро сходится. Во-первых, каждое следующее характеристическое число больше
- 21. Обозначим и прологарифмируем последнее выражение: . tР – время наступления регулярного режима. – темп охлаждения (нагрева),
- 22. Для граничных условий I рода при Fo ≥ 0,3 μ1 = . Величина называется темпом нагрева
- 24. Скачать презентацию










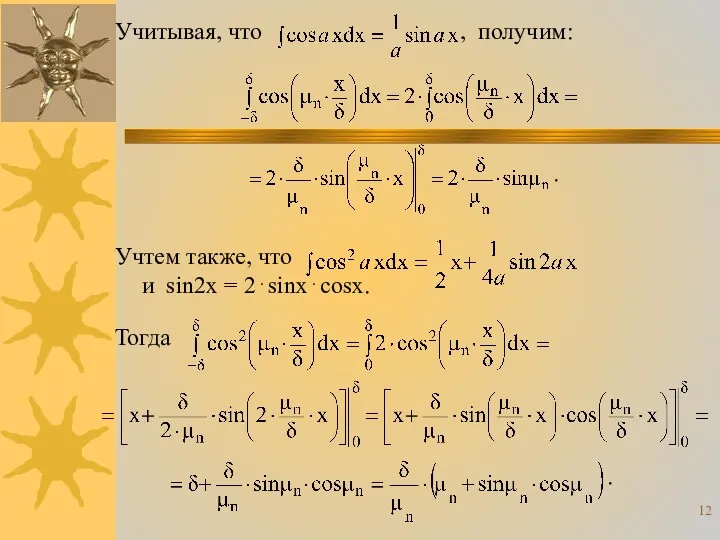










 Магнитные свойства горных пород и руд
Магнитные свойства горных пород и руд Масса, плотность, объем. 7 класс
Масса, плотность, объем. 7 класс Молекулярная физика
Молекулярная физика Компенсация реактивной мощности в системах электроснабжения промышленных предприятий
Компенсация реактивной мощности в системах электроснабжения промышленных предприятий Преобразователи электрических величин
Преобразователи электрических величин Определение давления тела на опору
Определение давления тела на опору : Слюсарно-механічні способи відновлення
: Слюсарно-механічні способи відновлення Тепловое излучение
Тепловое излучение Механические передачи. Ременные передачи
Механические передачи. Ременные передачи Разработка урока физики: Электризация тел
Разработка урока физики: Электризация тел Моделирование геомеханических процессов. Тема 11. Лекция № 16
Моделирование геомеханических процессов. Тема 11. Лекция № 16 Электронная презентация Два способа изменения внутренней энергии
Электронная презентация Два способа изменения внутренней энергии Масова частка речовини у розчині
Масова частка речовини у розчині Мультимедийная разработка внеклассного мероприятия Пионеры русской космонавтики
Мультимедийная разработка внеклассного мероприятия Пионеры русской космонавтики Режимы работы промышленных электрических сетей
Режимы работы промышленных электрических сетей Механические колебания
Механические колебания Презентация по физике Экология и космос
Презентация по физике Экология и космос Диодтыѕ атќаратын ќызметі
Диодтыѕ атќаратын ќызметі Проекты АЭС с ВВЭР Российские реакторы 3-го поколения
Проекты АЭС с ВВЭР Российские реакторы 3-го поколения Электризация тел. Электроскоп. Проводники и диэлектрики
Электризация тел. Электроскоп. Проводники и диэлектрики Подшипники скольжения
Подшипники скольжения Решение задач по физике (7 класс)
Решение задач по физике (7 класс) Цифровые сигналы
Цифровые сигналы Открытие электромагнитной индукции
Открытие электромагнитной индукции Измерение физических величин
Измерение физических величин Поверхностное натяжение. Термодинамика жидкостей
Поверхностное натяжение. Термодинамика жидкостей Своя игра по физике
Своя игра по физике Агрегатные состояния вещества. Плавление и отвердевание кристаллических тел
Агрегатные состояния вещества. Плавление и отвердевание кристаллических тел