Содержание
- 2. Последние два выражения образуют систему из 6N уравнений. Исключая из них время, получим (6N-1) функций С1,
- 3. Из всех 6N-1 интегралов движения наибольший интерес представляют аддитивные интегралы движения. Свойство аддитивности выражается в том,
- 4. Полный импульс замкнутой системы равен сумме импульсов, составляющих ее частиц (i = 1,…,N) 6.1 Закон сохранения
- 5. Сложим эти уравнения и объединим силы от пар частиц Но по третьему закону Ньютона , поэтому
- 6. Выразим импульс системы через скорость движения ее центра масс. Центром масс (центром инерции) системы тел называется
- 7. Здесь - скорость движения центра масс, она характеризует скорость перемещения системы как целого. Поскольку для замкнутой
- 8. Ранее был установлен закон сохранения полной механической энергии для одного тела - формула (4.3.1). Обобщим этот
- 9. Запишем уравнение Ньютона для i – ой частицы Умножим каждое из этих уравнений на элементарные перемещения
- 10. Левая часть уравнения (6.2.1) равна приращению кинетической энергии В правой части (6.2.1) первое слагаемое равно элементарной
- 11. - изменение расстояния между двумя частицами
- 12. Обобщим полученную формулу на случай N частиц Учтем, что внутренние силы центральные, направлены вдоль радиус-векторов ,
- 13. В результате получаем Объединяя слагаемые, формулу (6.2.1) перепишем в виде или Значит полная механическая энергия системы
- 14. 6.3 Закон сохранения момента импульса Ранее было получено выражение (5.5.5), связывающее момент импульса с моментом внешних
- 15. Если система замкнутая, то на каждую из ее частей внешние силы не действуют , тогда поэтому
- 16. Также всегда сохраняется проекция момента импульса на ту ось, относительно которой силовое поле симметрично. Частным случаем
- 17. 6.4 Упругий и неупругий удар шаров Анализ законов сохранения позволяет, не решая уравнений Ньютона, получить важные
- 18. Существуют два предельных вида удара: абсолютно упругий и абсолютно неупругий. При абсолютно упругом ударе механическая энергия
- 19. При абсолютно неупругом ударе потенциальная энергия деформации не возникает, а кинетическая энергия тел полностью или частично
- 20. Абсолютно неупругий удар Пусть массы шаров равны т1 и т2 , а скорости до удара и
- 21. Найдем, какая часть кинетической энергии перешла в немеханическую форму энергии (тепловую или другую) (6.4.2) Рассмотрим частный
- 22. Если, кроме того, масса неподвижного тела много больше массы движущегося тела, то Следовательно, в этом случае
- 23. Если, наоборот, неподвижное тело много легче подвижного, то Значит, в этом случае лишь небольшая доля кинетической
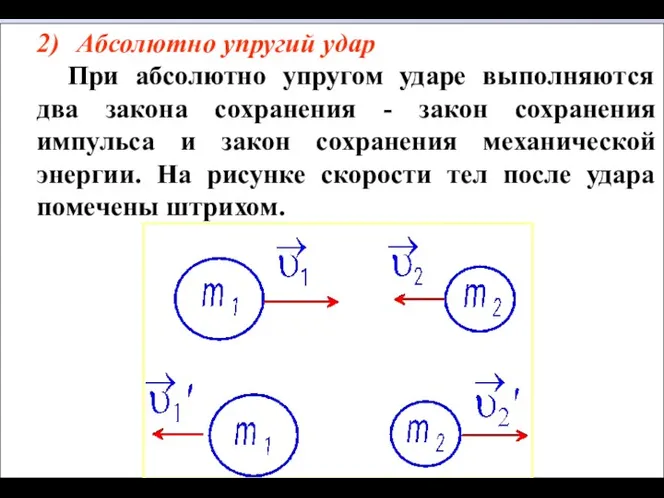
- 24. 2) Абсолютно упругий удар При абсолютно упругом ударе выполняются два закона сохранения - закон сохранения импульса
- 25. Запишем законы сохранения (6.4.3) Из них после преобразований получаем (6.4.4) Равенство (6.4.4) означает, что при абсолютно
- 26. Подставляя (6.4.4) в (6.4.3), получаем (6.4.5)
- 27. Рассмотрим частные случаи. 1) Пусть шары одинаковые, и один из шаров до удара был неподвижным, например,
- 29. Скачать презентацию

























 Законы геометрической оптики
Законы геометрической оптики Физика пласта
Физика пласта Элементарные частицы
Элементарные частицы урок-обобщение: Газовые законы
урок-обобщение: Газовые законы Передача давления жидкостями и газами. Закон Паскаля
Передача давления жидкостями и газами. Закон Паскаля Полупроводниковые дозиметрические детекторы
Полупроводниковые дозиметрические детекторы Свайные фундаменты. Классификация. (Лекция 6)
Свайные фундаменты. Классификация. (Лекция 6) Виды сил
Виды сил Конструкция и техническое обслуживание пассажирских вагонов
Конструкция и техническое обслуживание пассажирских вагонов Kosmicheskoe-izluchenie
Kosmicheskoe-izluchenie Учебный проект по теме Виды теплопередачи
Учебный проект по теме Виды теплопередачи Карданная передача
Карданная передача Презетанция Ток в вакууме
Презетанция Ток в вакууме Термическая стабильность структуры наноматериалов
Термическая стабильность структуры наноматериалов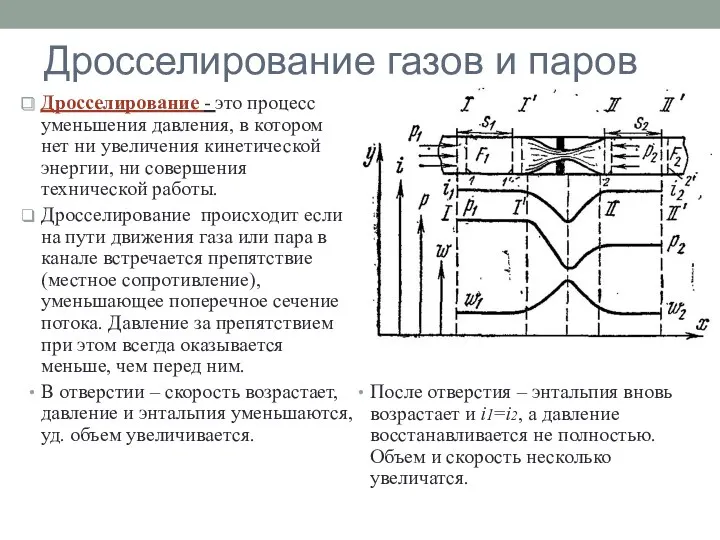 Дросселирование газов и паров
Дросселирование газов и паров Явление электромагнитной индукции
Явление электромагнитной индукции Спектральные характеристики одномерных и трехмерных жидкокристаллических фотонных кристаллов
Спектральные характеристики одномерных и трехмерных жидкокристаллических фотонных кристаллов Лекция № 1. Механические характеристики асинхронных электродвигателей
Лекция № 1. Механические характеристики асинхронных электродвигателей Занятие спецкурса о физике в 8 классе Бионика и электрические явления в живой природе
Занятие спецкурса о физике в 8 классе Бионика и электрические явления в живой природе Властивості рідин. Поверхневий натяг. Змочування
Властивості рідин. Поверхневий натяг. Змочування Відновлення деталей електролітичними способами. Зміцнення поверхонь
Відновлення деталей електролітичними способами. Зміцнення поверхонь Толық тізбек үшін Ом заңы
Толық тізбек үшін Ом заңы Кузнечно-сварочная практика. Специальность 190604 Техническое обслуживание и ремонт автомобильного транспорта
Кузнечно-сварочная практика. Специальность 190604 Техническое обслуживание и ремонт автомобильного транспорта Физико-технические основы электроэнергетики. Лекция 10
Физико-технические основы электроэнергетики. Лекция 10 Модульные технологии как технологии здоровьесбережения.
Модульные технологии как технологии здоровьесбережения. Фазированные антенные решетки и их назначение. Надежность ФАР
Фазированные антенные решетки и их назначение. Надежность ФАР Радиоактивность
Радиоактивность Подшипники качения
Подшипники качения