Содержание
- 2. Вопросы по теме: «ЧЕТЫРЁХУГОЛЬНИКИ». Ломаная. Замкнутая ломаная. Простая ломаная. Многоугольник. Вершины, стороны, диагонали и периметр многоугольника.
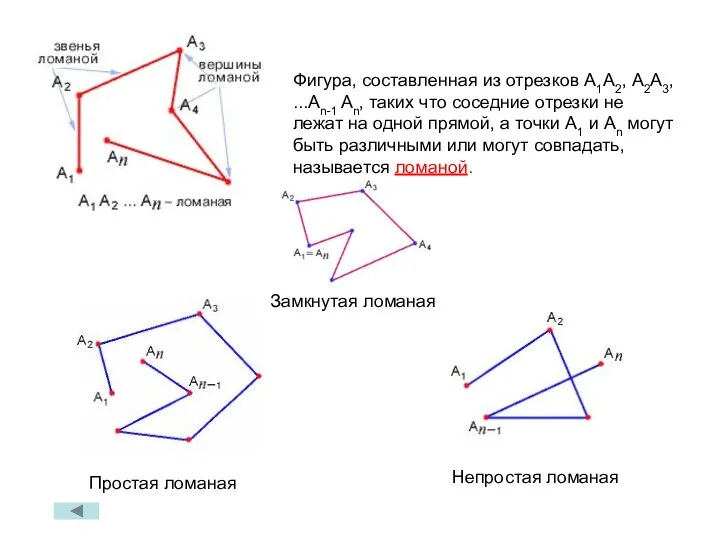
- 3. Непростая ломаная Простая ломаная Фигура, составленная из отрезков А1А2, А2А3, ...Аn-1 An, таких что соседние отрезки
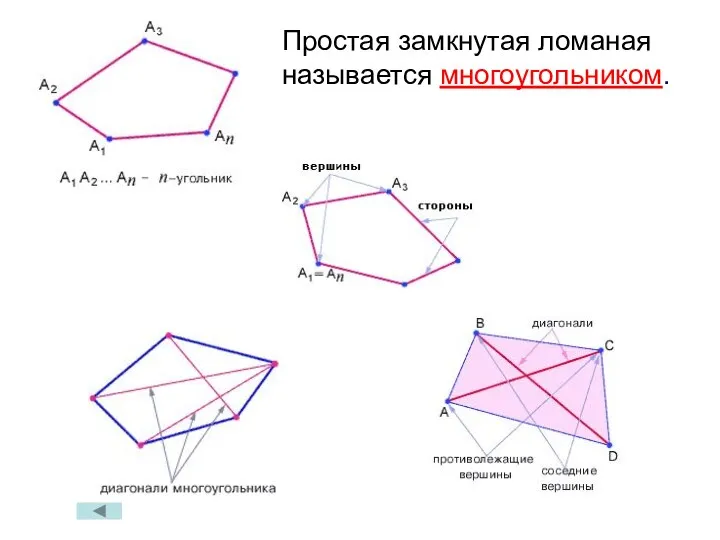
- 4. Простая замкнутая ломаная называется многоугольником.
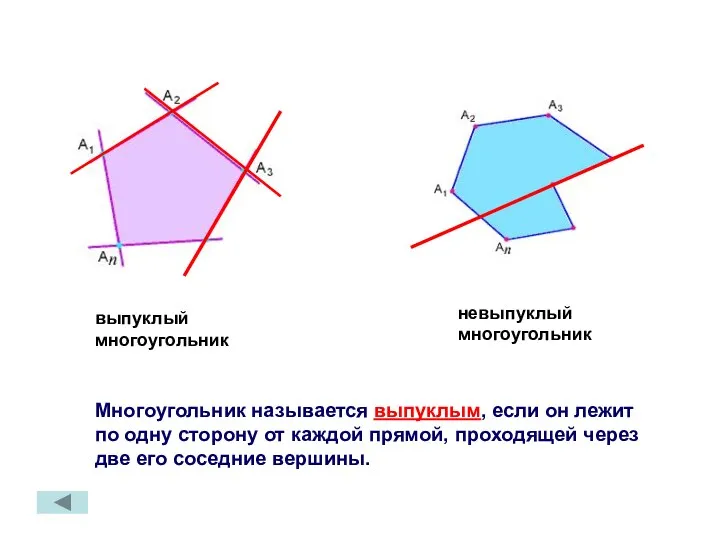
- 5. выпуклый многоугольник невыпуклый многоугольник Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой,
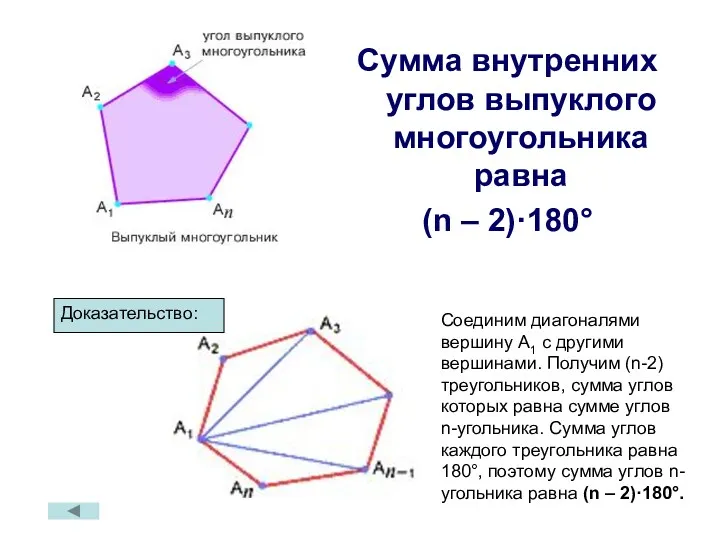
- 6. Сумма внутренних углов выпуклого многоугольника равна (n – 2)·180° Доказательство: Соединим диагоналями вершину А1 с другими
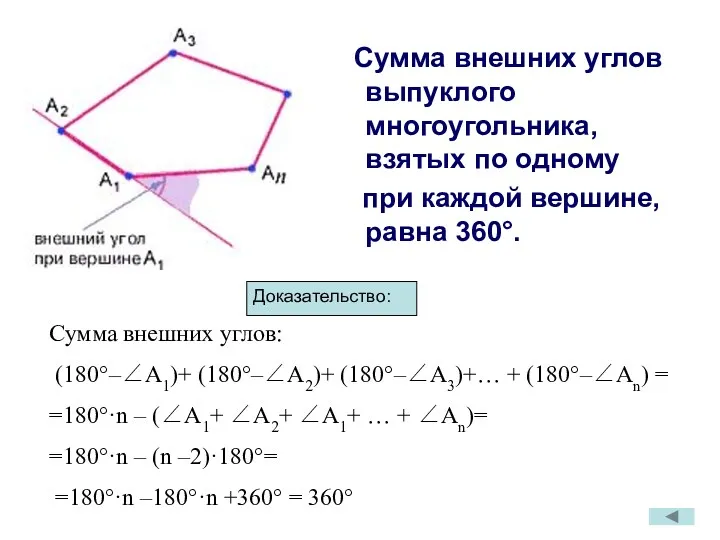
- 7. Сумма внешних углов выпуклого многоугольника, взятых по одному при каждой вершине, равна 360°. Доказательство: Сумма внешних
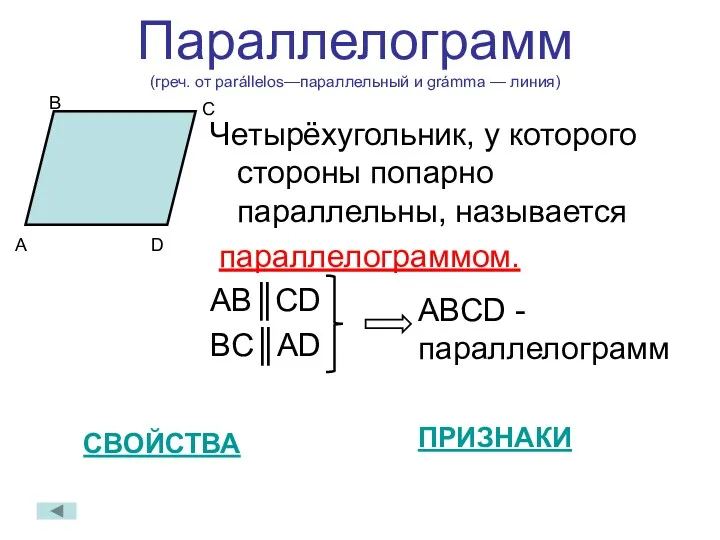
- 8. Параллелограмм (греч. от parállelos—параллельный и grámma — линия) Четырёхугольник, у которого стороны попарно параллельны, называется параллелограммом.
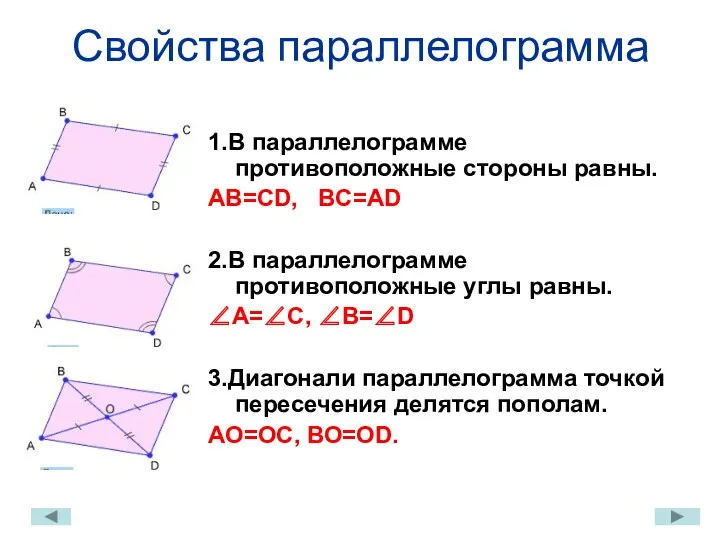
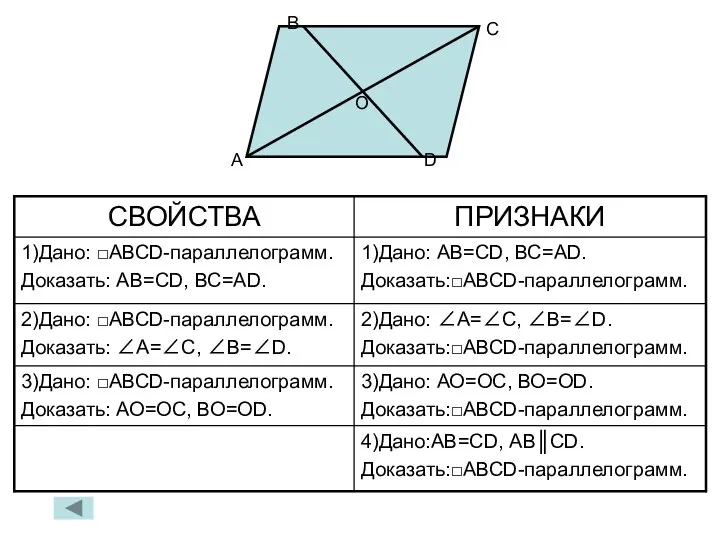
- 9. Свойства параллелограмма 1.В параллелограмме противоположные стороны равны. АВ=CD, BC=AD 2.В параллелограмме противоположные углы равны. ∠А=∠С, ∠В=∠D
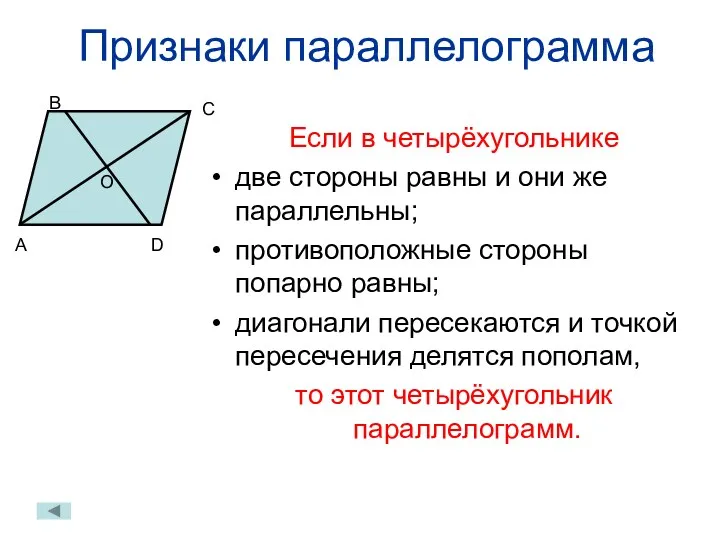
- 10. Признаки параллелограмма Если в четырёхугольнике две стороны равны и они же параллельны; противоположные стороны попарно равны;
- 11. А В С D О
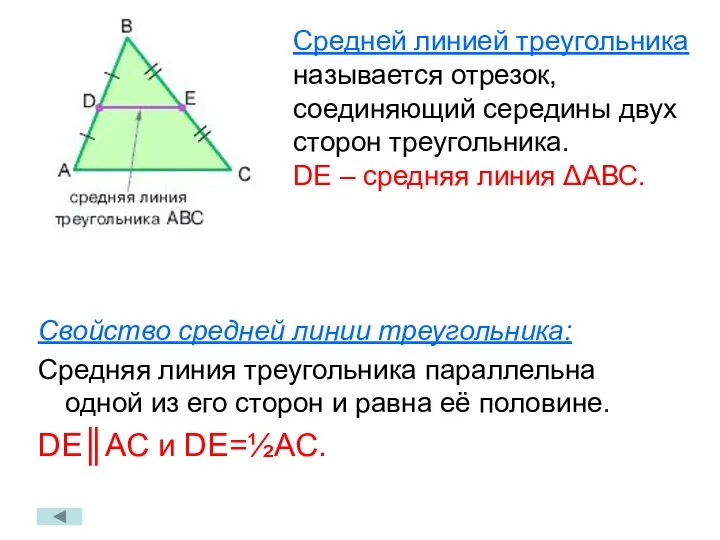
- 12. Свойство средней линии треугольника: Средняя линия треугольника параллельна одной из его сторон и равна её половине.
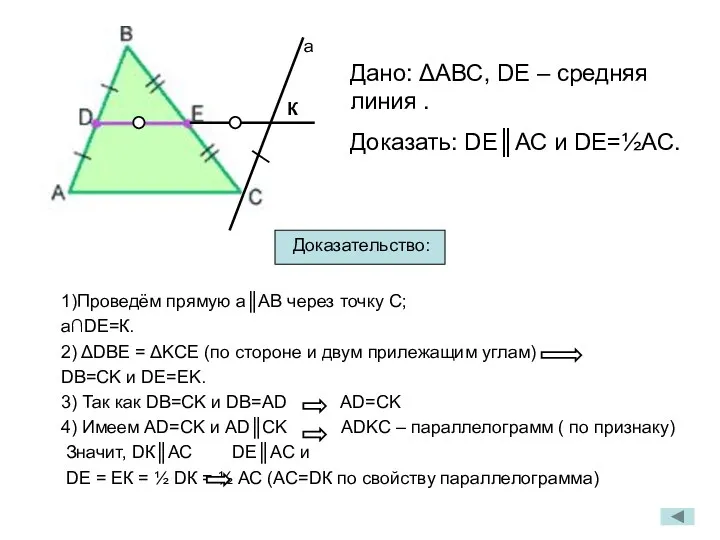
- 13. 1)Проведём прямую а║АВ через точку С; а∩DЕ=К. 2) ΔDBE = ΔKCE (по стороне и двум прилежащим
- 14. Фалéс из Милета — древнегреческий философ; военный инженер лидийских царей; совершал далекие путешествия с познавательными целями;
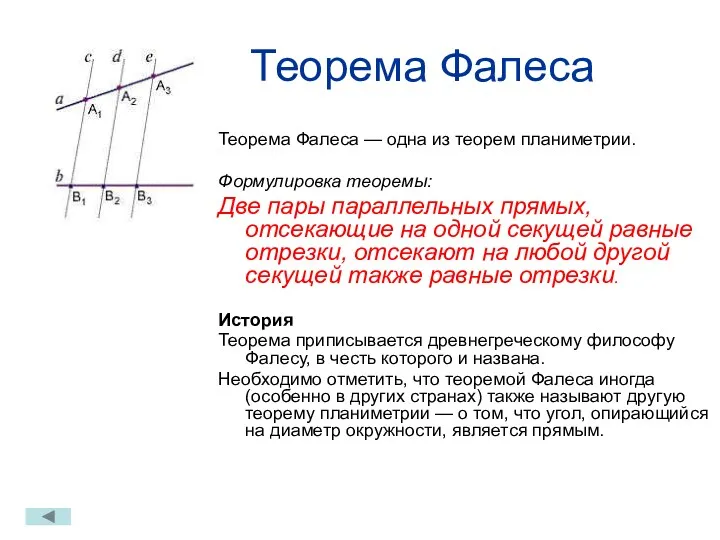
- 15. Теорема Фалеса Теорема Фалеса — одна из теорем планиметрии. Формулировка теоремы: Две пары параллельных прямых, отсекающие
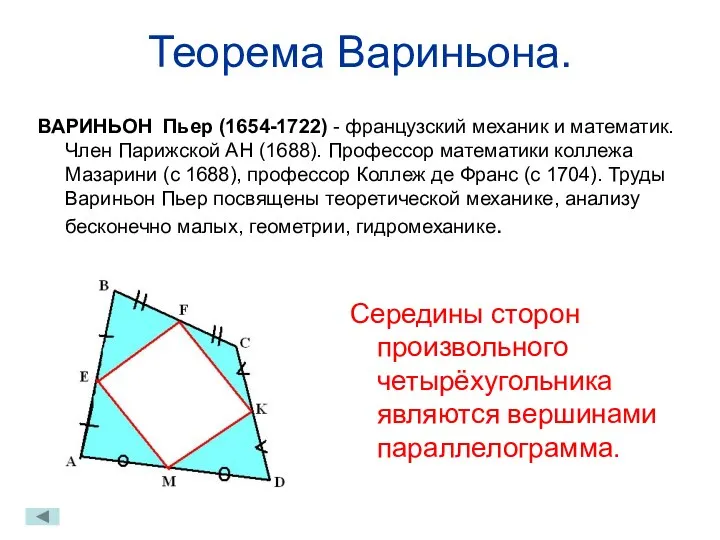
- 16. Теорема Вариньона. ВАРИНЬОН Пьер (1654-1722) - французский механик и математик. Член Парижской АН (1688). Профессор математики
- 17. трапеция Четырёхугольник, у которого две стороны параллельны, а две другие не параллельны, называется трапецией. Параллельные стороны
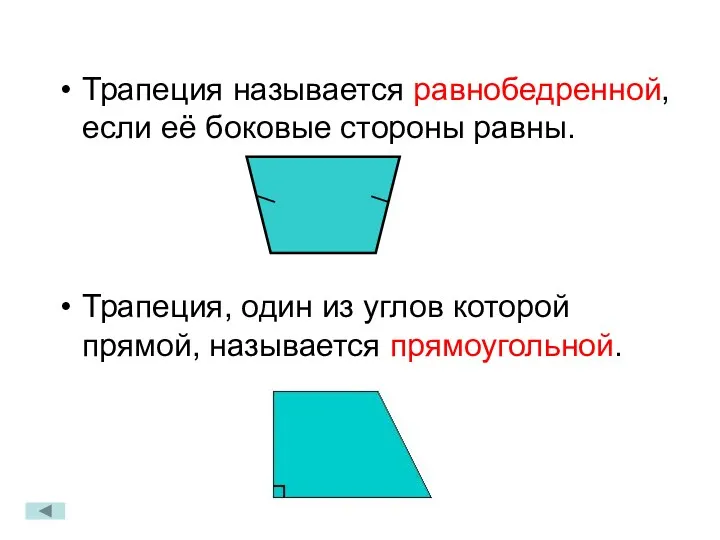
- 18. Трапеция называется равнобедренной, если её боковые стороны равны. Трапеция, один из углов которой прямой, называется прямоугольной.
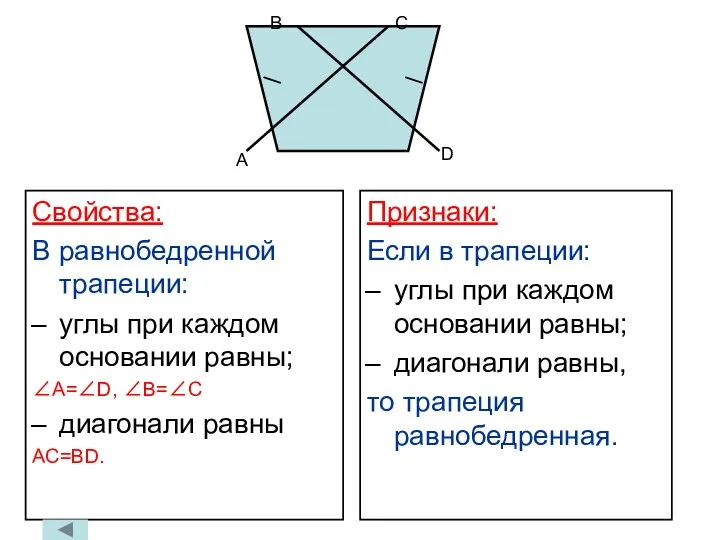
- 19. А В С D Свойства: В равнобедренной трапеции: углы при каждом основании равны; ∠А=∠D, ∠В=∠С диагонали
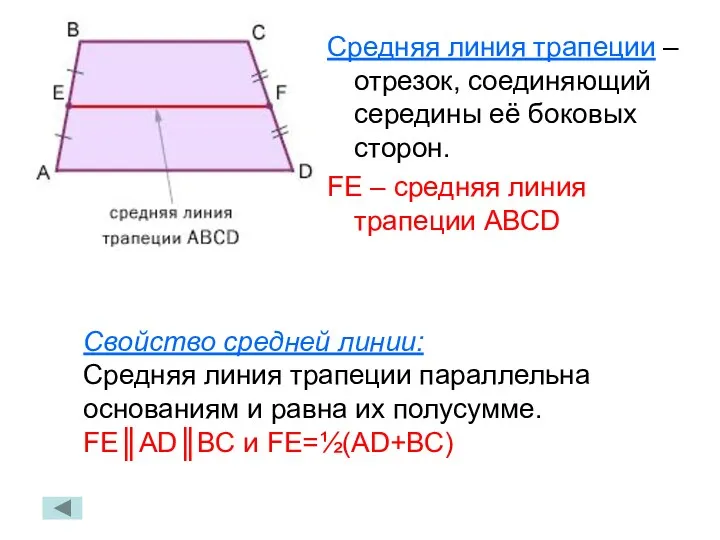
- 20. Средняя линия трапеции – отрезок, соединяющий середины её боковых сторон. FE – средняя линия трапеции АВСD
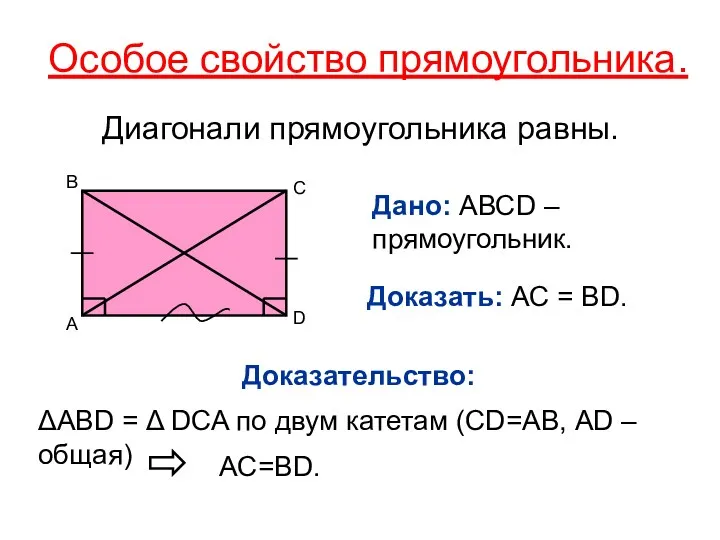
- 21. прямоугольник Прямоугольником называется параллелограмм, у которого все углы прямые. Свойства. Особое свойство прямоугольника: Диагонали прямоугольника равны.
- 22. Особое свойство прямоугольника. Диагонали прямоугольника равны. Дано: АВСD – прямоугольник. A B C D Доказательство: ΔАВD
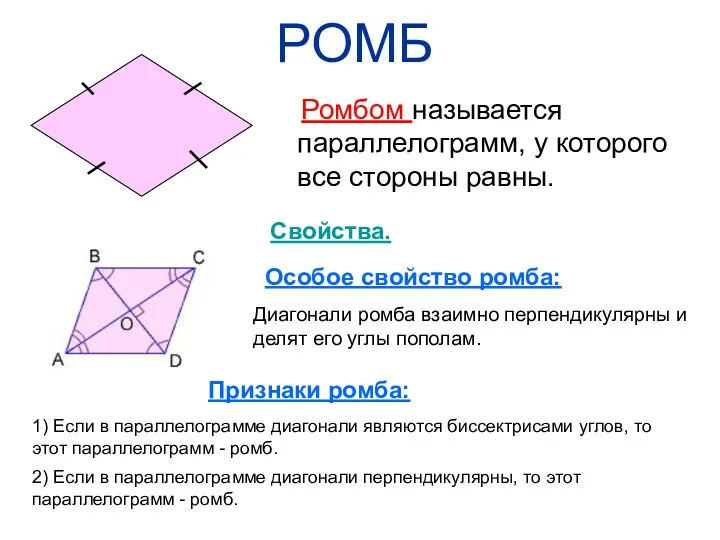
- 23. РОМБ Ромбом называется параллелограмм, у которого все стороны равны. Свойства. Особое свойство ромба: Диагонали ромба взаимно
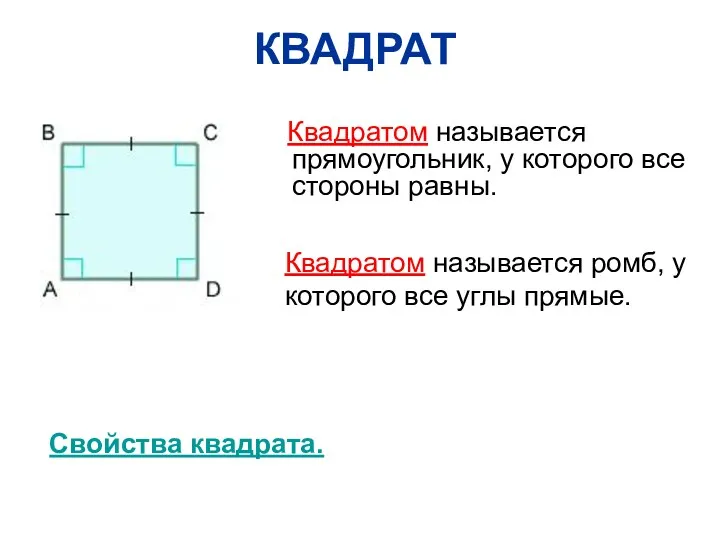
- 24. КВАДРАТ Квадратом называется прямоугольник, у которого все стороны равны. Квадратом называется ромб, у которого все углы
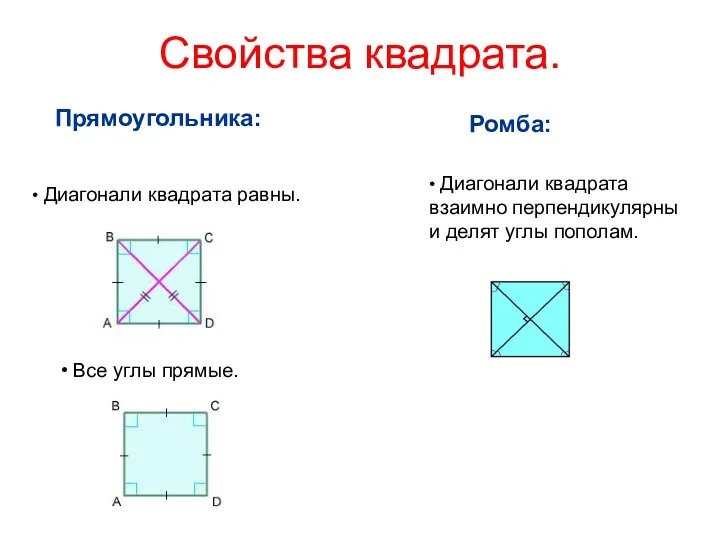
- 25. Свойства квадрата. Прямоугольника: • Диагонали квадрата равны. • Все углы прямые. Ромба: • Диагонали квадрата взаимно
- 27. Скачать презентацию




 Тест-презентация, на тему Площадь плоских фигур по геометрии в 8 классе.
Тест-презентация, на тему Площадь плоских фигур по геометрии в 8 классе. Решение задач на параллельные прямые
Решение задач на параллельные прямые зачет по геометрии по теме Треугольники
зачет по геометрии по теме Треугольники Наглядное пособие по геометрии
Наглядное пособие по геометрии Презентация Такая известная теорема Пифагора
Презентация Такая известная теорема Пифагора Урок математики в 8 классе по теме Многоугольники
Урок математики в 8 классе по теме Многоугольники Презентация Элементы стереометрии (9 класс)
Презентация Элементы стереометрии (9 класс) Своя игра
Своя игра обобщение материала по теме Четырехугольники
обобщение материала по теме Четырехугольники Повторение планиметрии.
Повторение планиметрии. к урокам 17-18 по геометрии 7 кл
к урокам 17-18 по геометрии 7 кл Презентация к уроку геометрии в 8 классе по теме: Теорема Пифагора
Презентация к уроку геометрии в 8 классе по теме: Теорема Пифагора Урок по теме Теорема Пифагора
Урок по теме Теорема Пифагора Золотое сечение
Золотое сечение урок по геометрии Четырехугольники
урок по геометрии Четырехугольники Презентация по теме Тетраэдр
Презентация по теме Тетраэдр Координаты вектора
Координаты вектора Аксиома параллельных прямых
Аксиома параллельных прямых уроки заключительного повторения по теме Пирамида
уроки заключительного повторения по теме Пирамида Площадь. Площадь прямоугольника
Площадь. Площадь прямоугольника Математическая игра Поле чудес
Математическая игра Поле чудес Основное свойство измерения углов
Основное свойство измерения углов Симметрия вокруг нас
Симметрия вокруг нас Урок-презентация-игра, 7 класс, Геометрия Знаете ли вы геометрию?
Урок-презентация-игра, 7 класс, Геометрия Знаете ли вы геометрию? презентация к уроку геометрии в 11а классе - тела вращения
презентация к уроку геометрии в 11а классе - тела вращения ПРЕЗЕНТАЦИЯ ПО ТЕМЕ ТРЕУГОЛЬНИК
ПРЕЗЕНТАЦИЯ ПО ТЕМЕ ТРЕУГОЛЬНИК Проект по теме Арифметическая и геометрическая прогрессии
Проект по теме Арифметическая и геометрическая прогрессии Параллельные прямые
Параллельные прямые