Содержание
- 2. Теорема косинусов. История. Утверждения, обобщающие теорему Пифагора и эквивалентные теореме косинусов, были сформулированы отдельно для случаев
- 3. Теорема косинусов. История. Утверждения, эквивалентные теореме косинусов для сферического треугольника, применялись в сочинениях математиков стран Средней
- 4. Теорема косинусов. История. В Европе теорему косинусов популяризовал Франсуа Виет в XVI столетии. В начале XIX
- 5. Теорема косинусов Теорема: Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих
- 6. Теорема косинусов Доказательство: Пусть в треугольнике ABC AB=c, BC=a, CA=b. Докажем, например, что: Введем систему координат
- 9. Теорема синусов. История. Самое древнее доказательство для теоремы синусов на плоскости описано в книге Насир ад-Дин
- 10. Теорема синусов Теорема: Стороны треугольника пропорциональны синусам противолежащих углов.
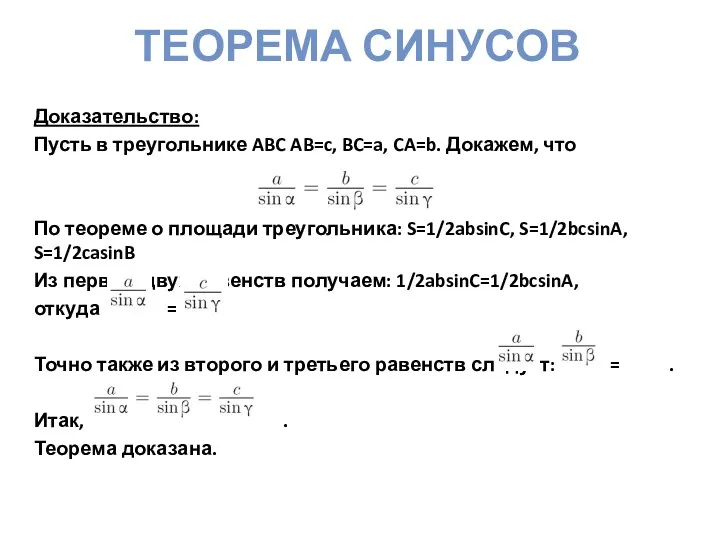
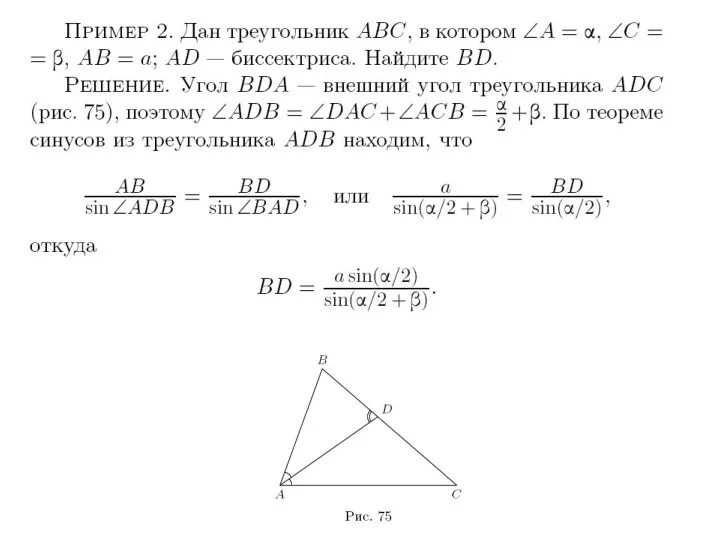
- 11. Теорема синусов Доказательство: Пусть в треугольнике ABC AB=c, BC=a, CA=b. Докажем, что По теореме о площади
- 12. Теорема синусов Замечание: Можно доказать, что отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной
- 16. Скачать презентацию











 Треугольники
Треугольники Методическая разработка урока по теме Симметрия 8 класс
Методическая разработка урока по теме Симметрия 8 класс презентация к уроку геометрии 8 класс
презентация к уроку геометрии 8 класс Медианы, биссектрисы и высоты треугольника (тест)
Медианы, биссектрисы и высоты треугольника (тест) Презентация к уроку Конус 11 класс
Презентация к уроку Конус 11 класс Луч и угол
Луч и угол презентация геометрия 8 класс: Параллелограмм
презентация геометрия 8 класс: Параллелограмм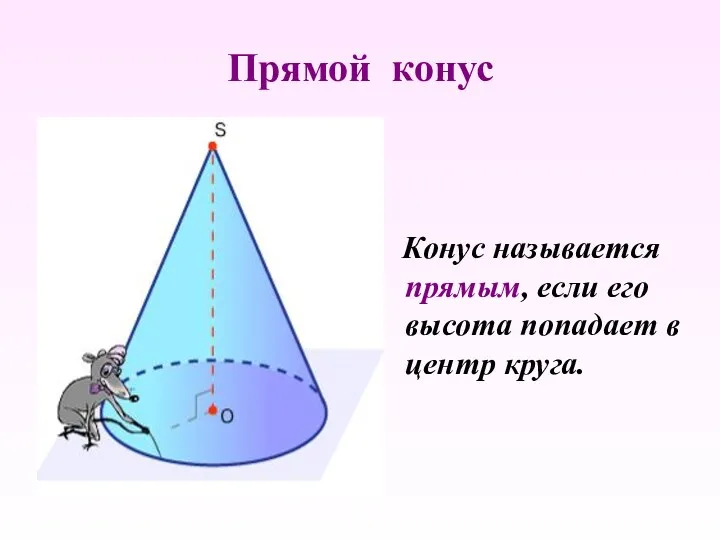 Презентация Определение конуса
Презентация Определение конуса Урок геометрии в 8 классе Площадь трапеции
Урок геометрии в 8 классе Площадь трапеции Презентация по геометрии
Презентация по геометрии Прямоугольные треугольники
Прямоугольные треугольники Начальные геометрические сведения
Начальные геометрические сведения Презентация
Презентация Пифагор
Пифагор Свойства прямоугольного треугольника
Свойства прямоугольного треугольника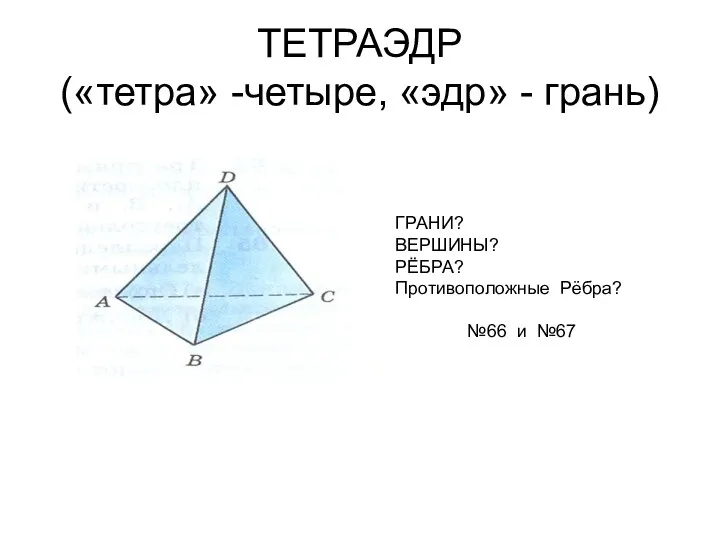 тетраэдр и параллелепипед
тетраэдр и параллелепипед Стереометрия 10 класс. Двугранный угол. Перпендикулярность плоскостей. Прямоугольный параллелепипед.
Стереометрия 10 класс. Двугранный угол. Перпендикулярность плоскостей. Прямоугольный параллелепипед. Исторический материал Начала геометрии
Исторический материал Начала геометрии ЭЛЕКТИВНЫЙ КУРС РЕШЕНИЕ ПЛАНИМЕТРИЧЕСКИХ ЗАДАЧ НА ВПИСАННЫЕ И ОПИСАННЫЕ ОКРУЖНОСТИ по геометрии для учащихся 9 классов
ЭЛЕКТИВНЫЙ КУРС РЕШЕНИЕ ПЛАНИМЕТРИЧЕСКИХ ЗАДАЧ НА ВПИСАННЫЕ И ОПИСАННЫЕ ОКРУЖНОСТИ по геометрии для учащихся 9 классов 7 чудес света
7 чудес света Сечение тетраэдра
Сечение тетраэдра Урок-обобщение по теме Параллельные прямые
Урок-обобщение по теме Параллельные прямые Методическая разработка по теме Признаки равенства треугольников
Методическая разработка по теме Признаки равенства треугольников Презентация Построения в пространстве. Геометрия 10 класс.
Презентация Построения в пространстве. Геометрия 10 класс. Презентация по теме: Подобие теругольников
Презентация по теме: Подобие теругольников Презентация Второй признак равенства треугольников
Презентация Второй признак равенства треугольников Правильные многогранники
Правильные многогранники Презентация к уроку по теме: Площадь (8 класс)
Презентация к уроку по теме: Площадь (8 класс)