Содержание
- 2. Прямая и плоскость пересекаются, если они имеют одну единственную общую точку, которую называют точкой пересечения прямой
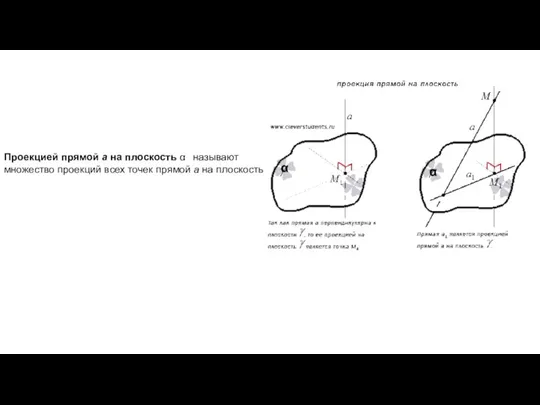
- 3. Проекцией точки М на плоскость α называется либо сама точка М, если М лежит в плоскости
- 4. Проекцией прямой a на плоскость α называют множество проекций всех точек прямой a на плоскость .
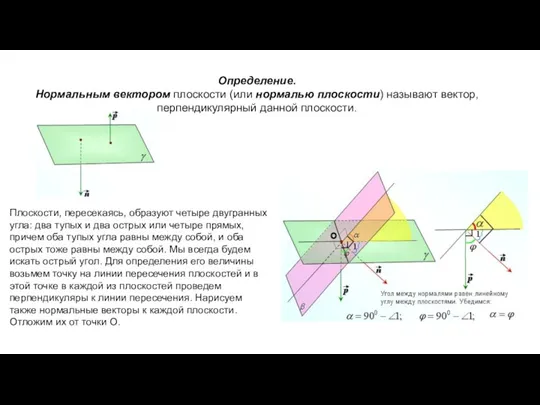
- 6. Определение. Нормальным вектором плоскости (или нормалью плоскости) называют вектор, перпендикулярный данной плоскости. Плоскости, пересекаясь, образуют четыре
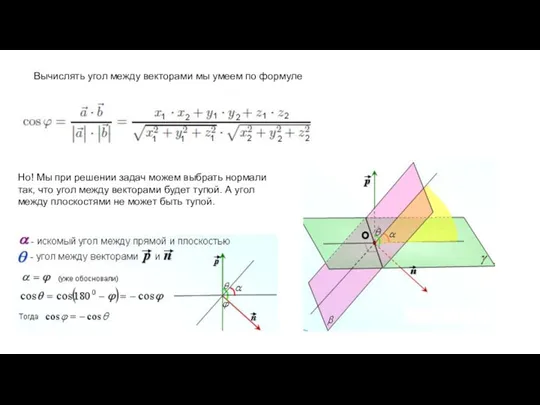
- 7. Вычислять угол между векторами мы умеем по формуле Но! Мы при решении задач можем выбрать нормали
- 8. Итак, если угол между нормалями острый, то мы сразу получаем угол между плоскостями (формула со знаком
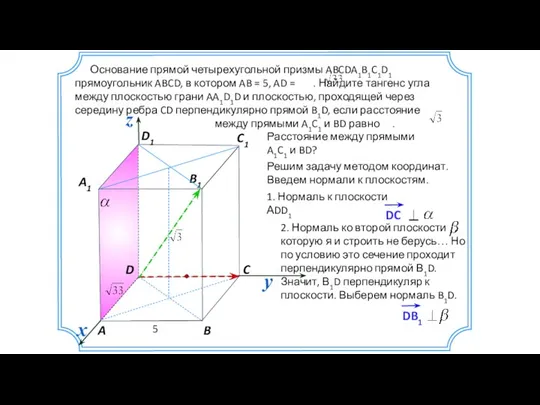
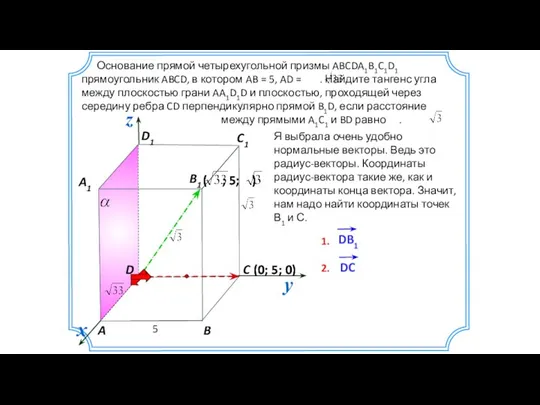
- 10. Основание прямой четырехугольной призмы ABCDA1B1C1D1 прямоугольник ABCD, в котором AB = 5, AD = . Найдите
- 11. (0; 5; 0) Основание прямой четырехугольной призмы ABCDA1B1C1D1 прямоугольник ABCD, в котором AB = 5, AD
- 13. Скачать презентацию





 Презентация по теме Прямоугольные треугольники 7 класс учебник Атанасяна
Презентация по теме Прямоугольные треугольники 7 класс учебник Атанасяна Введение в геометрию. Прямая и ортезок.
Введение в геометрию. Прямая и ортезок. 7класс Геометрия Перпендикулярные прямые
7класс Геометрия Перпендикулярные прямые к уроку № 30 по геометрии 7 кл
к уроку № 30 по геометрии 7 кл Презентация Значение синуса, косинуса и тангенса для углов 30°, 45°, 60°
Презентация Значение синуса, косинуса и тангенса для углов 30°, 45°, 60° Презентация к уроку геометрии Вектора в координатной плоскости. 9 класс.
Презентация к уроку геометрии Вектора в координатной плоскости. 9 класс. Урок по геометрии: Второй признак равенства треугольников 7 класс
Урок по геометрии: Второй признак равенства треугольников 7 класс Презентация. Площадь и периметр прямоугольника.
Презентация. Площадь и периметр прямоугольника. Свойства и признаки треугольников
Свойства и признаки треугольников Соотношение между сторонами и углами прямоугольного треугольника
Соотношение между сторонами и углами прямоугольного треугольника конспект урока на тему прямоугольник 8 класс
конспект урока на тему прямоугольник 8 класс Презентация Треугольник
Презентация Треугольник Презентация решения задач по теме Треугольник
Презентация решения задач по теме Треугольник Интерактивный плакат на тему Четырехугольники
Интерактивный плакат на тему Четырехугольники Презентация Пифагор и его школа
Презентация Пифагор и его школа Обобщающий урок геометрии за курс 8 класса
Обобщающий урок геометрии за курс 8 класса Некоторые задачи из пособия Гордина Задачи С 4 для подготовки к ЕГЭ по математике
Некоторые задачи из пособия Гордина Задачи С 4 для подготовки к ЕГЭ по математике Основное свойство измерения углов
Основное свойство измерения углов Многогранники.
Многогранники. Решение задач по теме Многогранники, геометрия, 10 класс
Решение задач по теме Многогранники, геометрия, 10 класс Первый урок геометрии в 8 классе
Первый урок геометрии в 8 классе Перпендикуляр и наклонная
Перпендикуляр и наклонная Урок по теме: Площади многоугольников. 8 класс. Геометрия. Учебник Л.С.Атанасян.
Урок по теме: Площади многоугольников. 8 класс. Геометрия. Учебник Л.С.Атанасян. Брейн - ринг по теме История математики
Брейн - ринг по теме История математики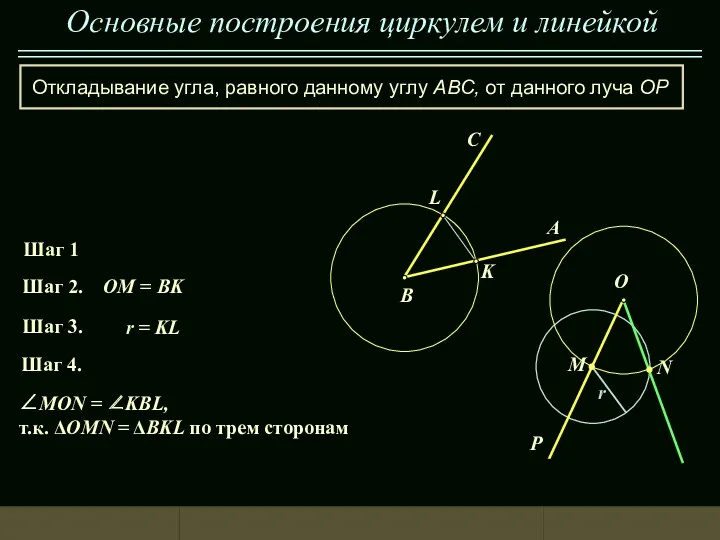 Построение угла равного данному
Построение угла равного данному Презентация по теме Метод координат
Презентация по теме Метод координат Вписанные и центральные углы
Вписанные и центральные углы Симметрия
Симметрия