Содержание
- 2. Применение теории графов Определения
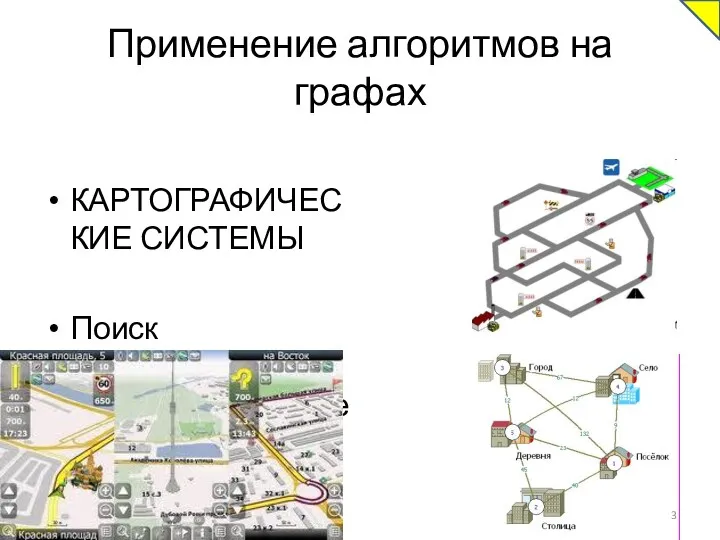
- 3. Применение алгоритмов на графах КАРТОГРАФИЧЕСКИЕ СИСТЕМЫ Поиск оптимального маршрута на карте
- 4. Применение алгоритмов на графах Различные приложения для компьютерных игр.
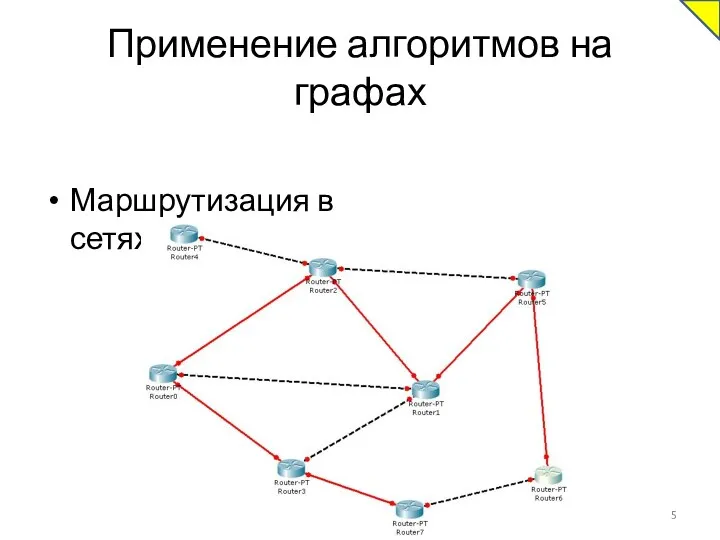
- 5. Применение алгоритмов на графах Маршрутизация в сетях
- 6. Социальные сети
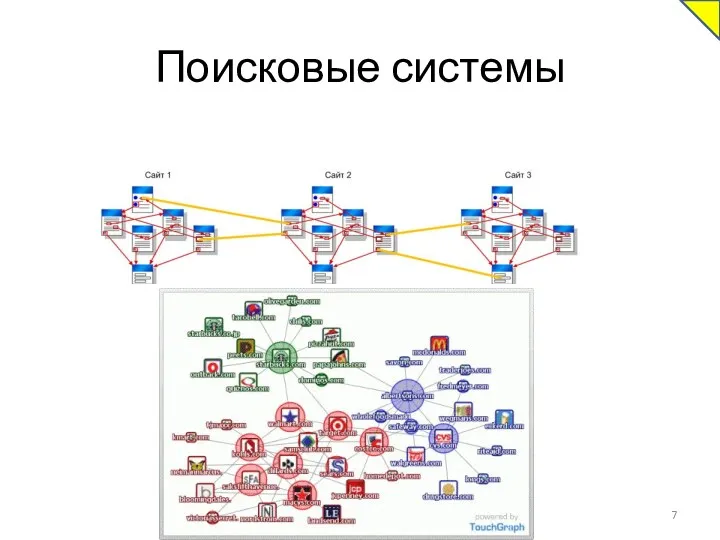
- 7. Поисковые системы
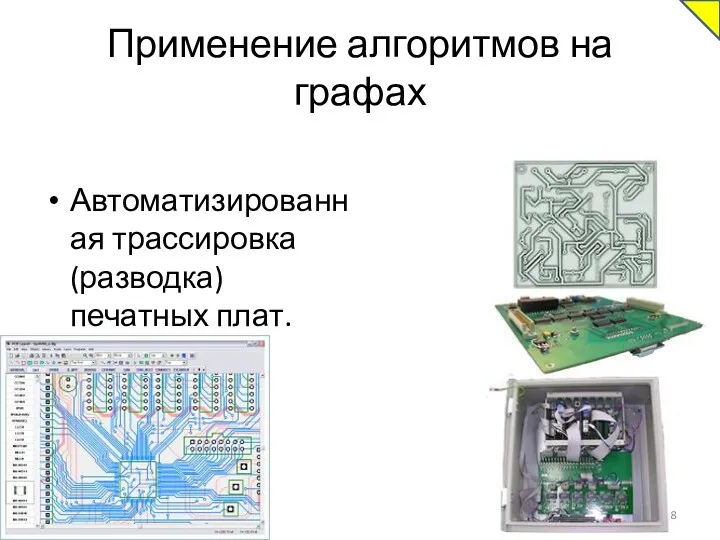
- 8. Применение алгоритмов на графах Автоматизированная трассировка (разводка) печатных плат.
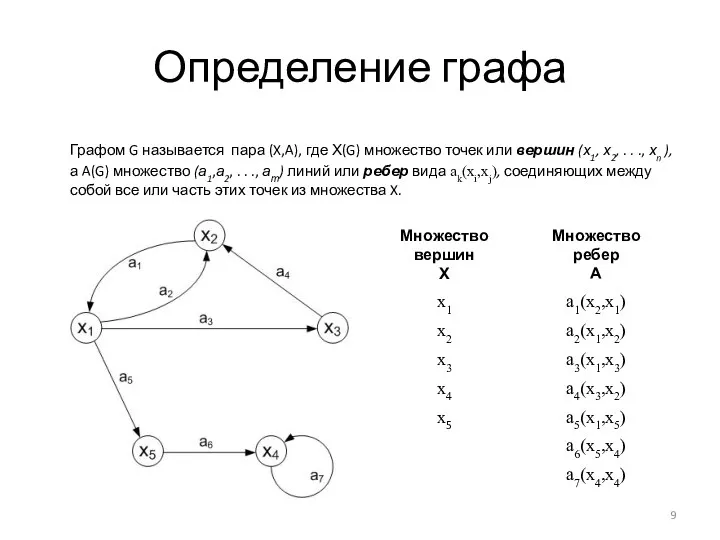
- 9. Определение графа Графом G называется пара (X,A), где Х(G) множество точек или вершин (х1, х2, .
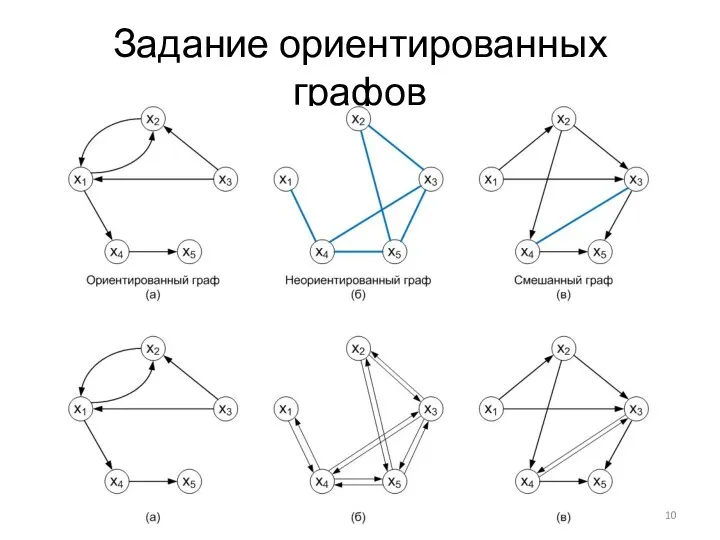
- 10. Задание ориентированных графов
- 11. Пути и маршруты Путем (или ориентированным маршрутом) ориентированного графа называется последовательность дуг, в которой конечная вершина
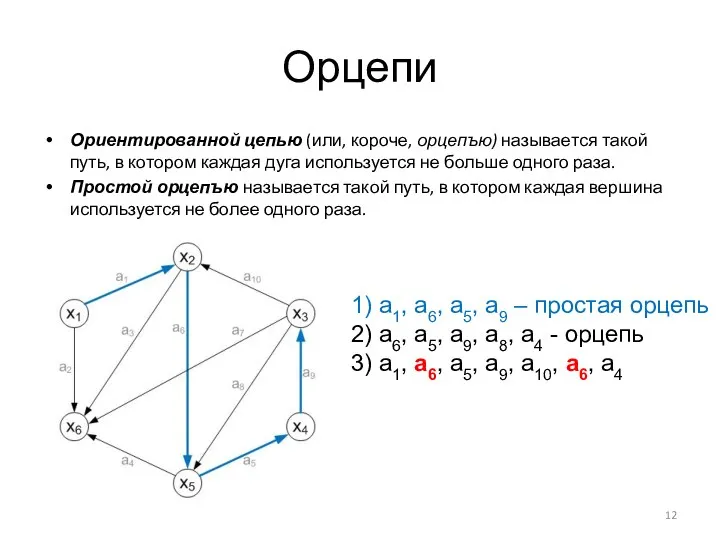
- 12. Орцепи Ориентированной цепью (или, короче, орцепъю) называется такой путь, в котором каждая дуга используется не больше
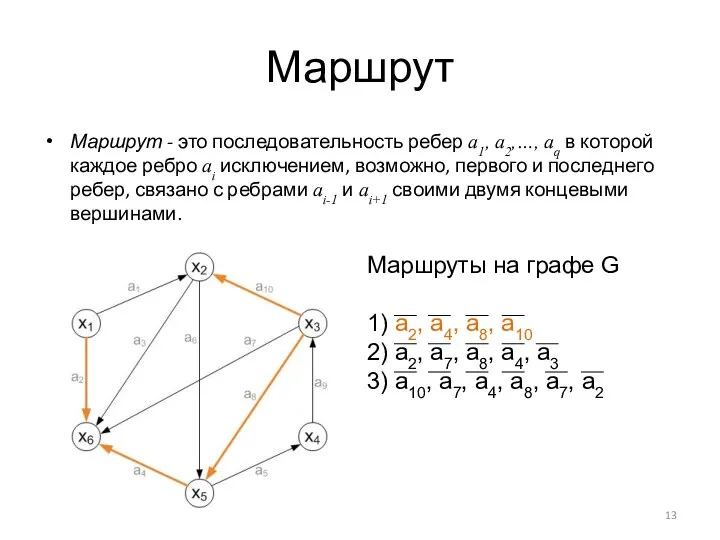
- 13. Маршрут Маршрут - это последовательность ребер a1, a2,…, aq в которой каждое ребро ai исключением, возможно,
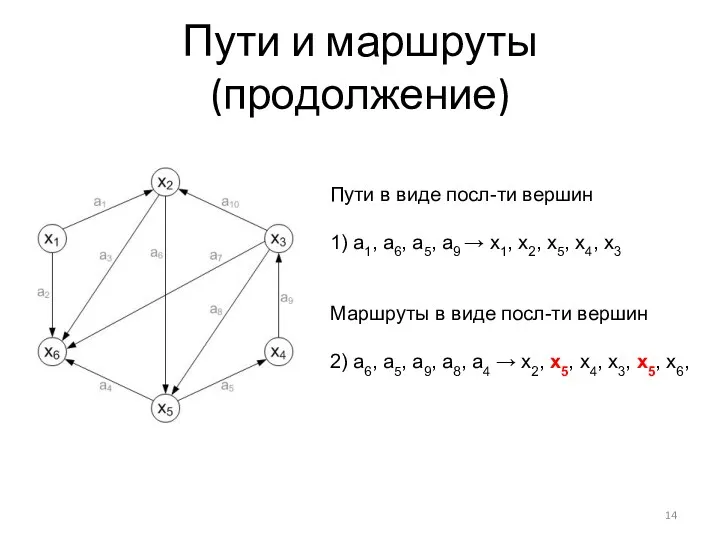
- 14. Пути и маршруты (продолжение) Пути в виде посл-ти вершин 1) a1, a6, a5, a9 → x1,
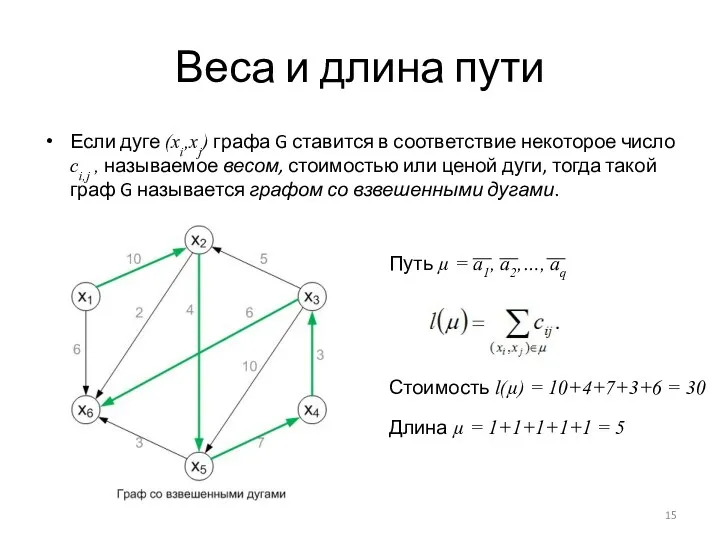
- 15. Веса и длина пути Если дуге (xi,xj) графа G ставится в соответствие некоторое число сi,j ,
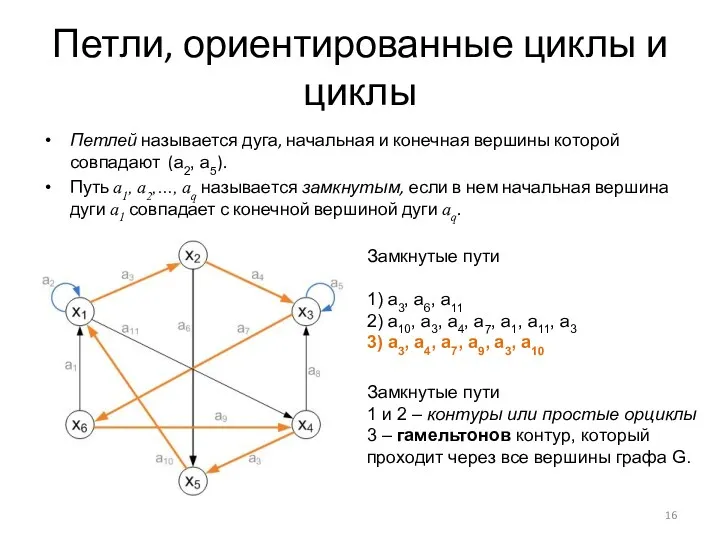
- 16. Петли, ориентированные циклы и циклы Петлей называется дуга, начальная и конечная вершины которой совпадают (a2, a5).
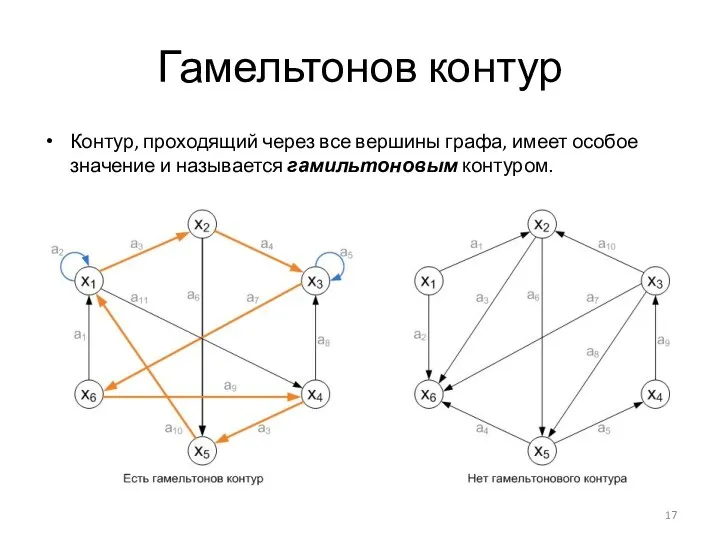
- 17. Гамельтонов контур Контур, проходящий через все вершины графа, имеет особое значение и называется гамильтоновым контуром.
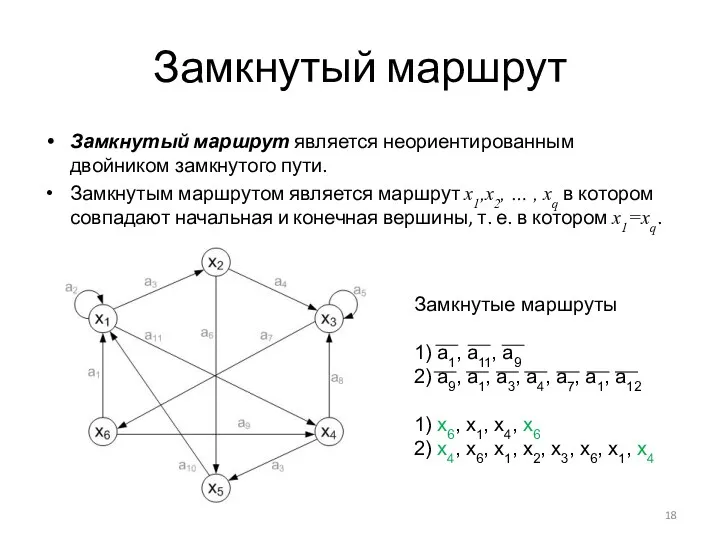
- 18. Замкнутый маршрут Замкнутый маршрут является неориентированным двойником замкнутого пути. Замкнутым маршрутом является маршрут x1,x2, … ,
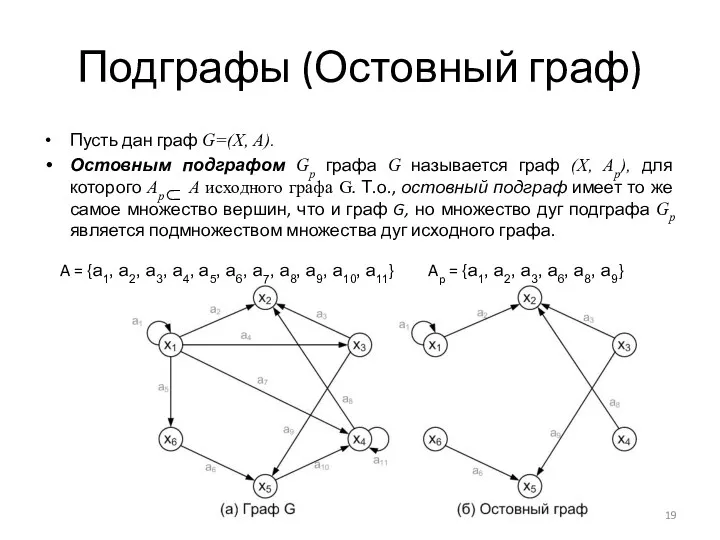
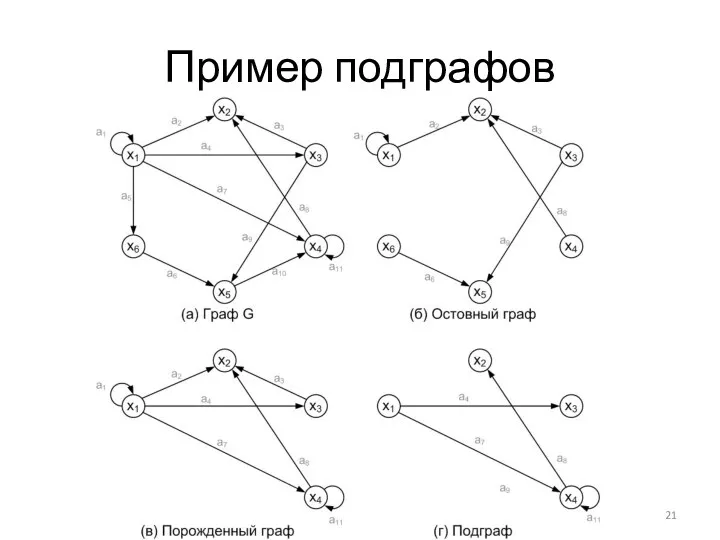
- 19. Подграфы (Остовный граф) Пусть дан граф G=(X, А). Остовным подграфом Gp графа G называется граф (X,
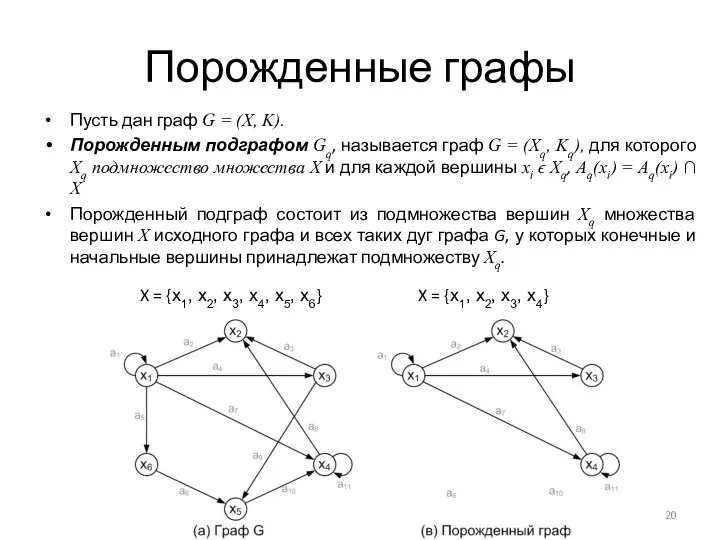
- 20. Порожденные графы Пусть дан граф G = (X, K). Порожденным подграфом Gq, называется граф G =
- 21. Пример подграфов
- 22. Хранение графов
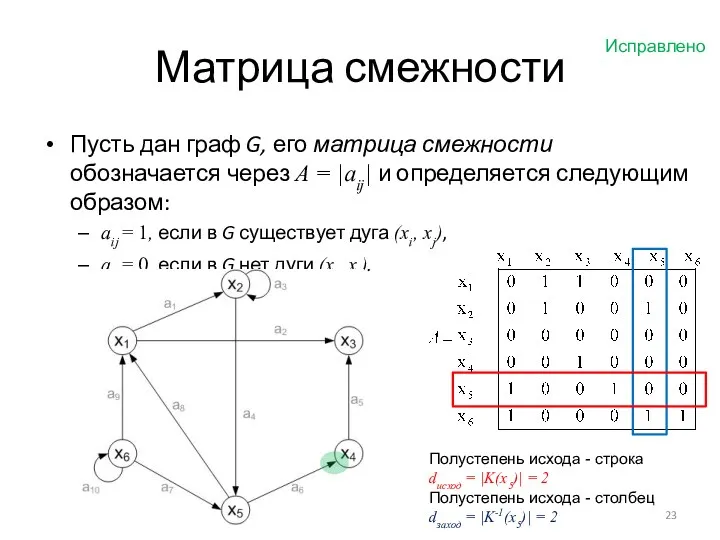
- 23. Матрица смежности Пусть дан граф G, его матрица смежности обозначается через A = |aij| и определяется
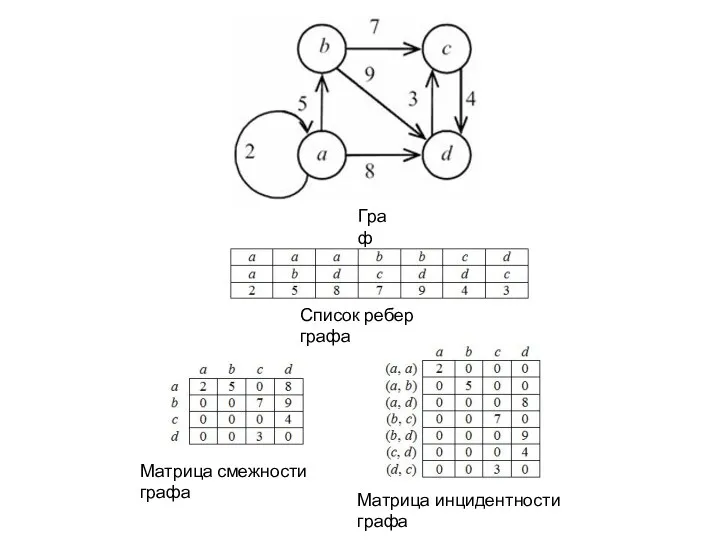
- 24. Матрица инцидентности Пусть дан граф G с n вершинами и т дугами. Матрица инциденций (инцидентности) графа
- 26. Алгоритмы на графах Обходные алгоритмы Обход в глубину (Depth First Search, DFS); Обход в ширину (Breadth
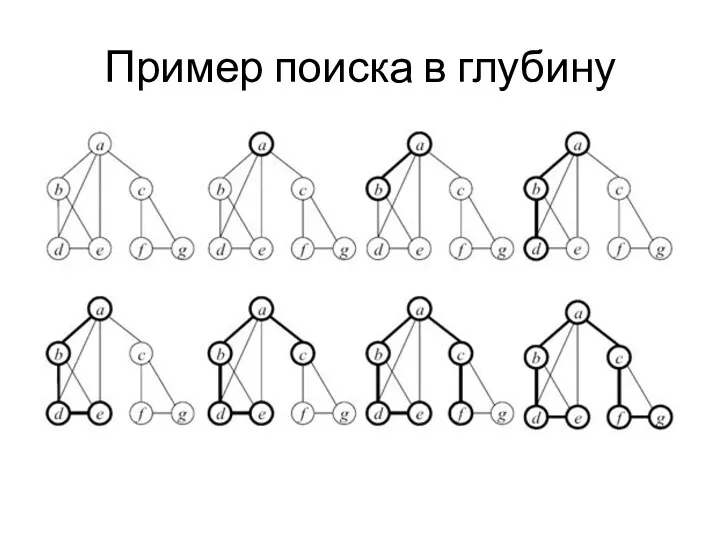
- 27. Поиск в глубину Алгоритм поиска в глубину Шаг 1. Всем вершинам графа присваивается значение не посещенная.
- 28. Пример поиска в глубину
- 29. Поиск в ширину Алгоритм поиска в ширину Шаг 1. Всем вершинам графа присваивается значение не посещенная.
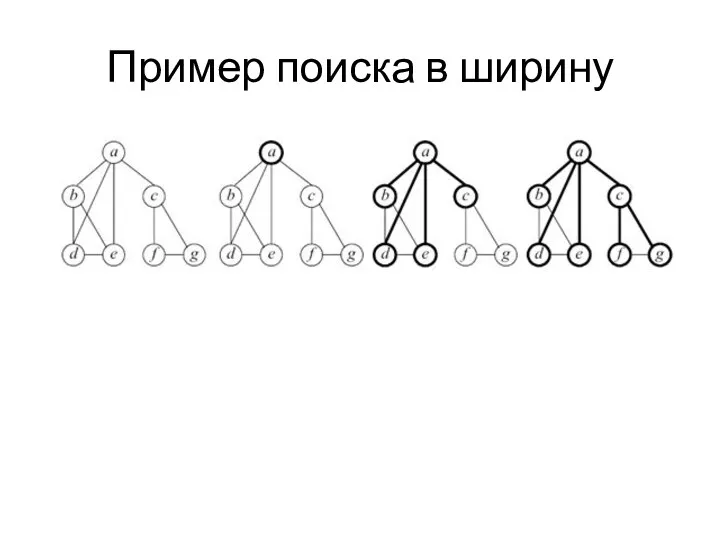
- 30. Пример поиска в ширину
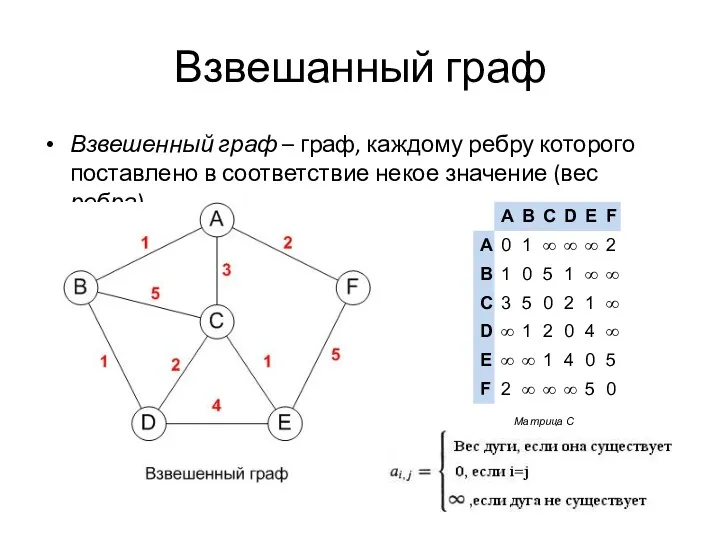
- 31. Взвешанный граф Взвешенный граф – граф, каждому ребру которого поставлено в соответствие некое значение (вес ребра).
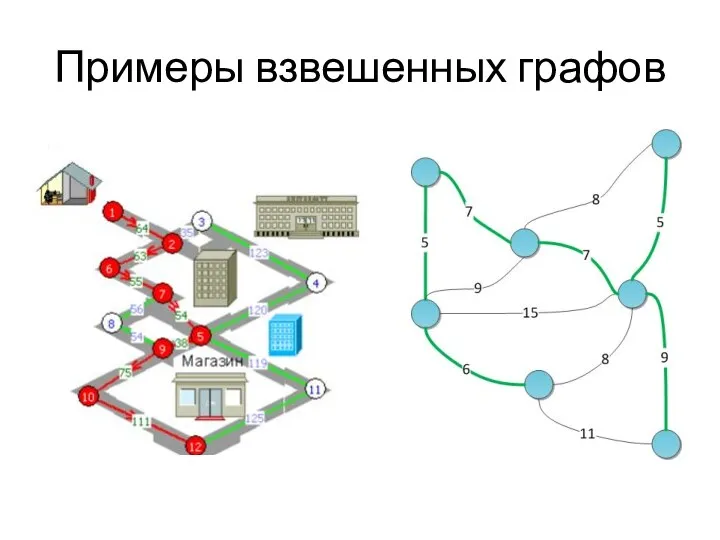
- 32. Примеры взвешенных графов
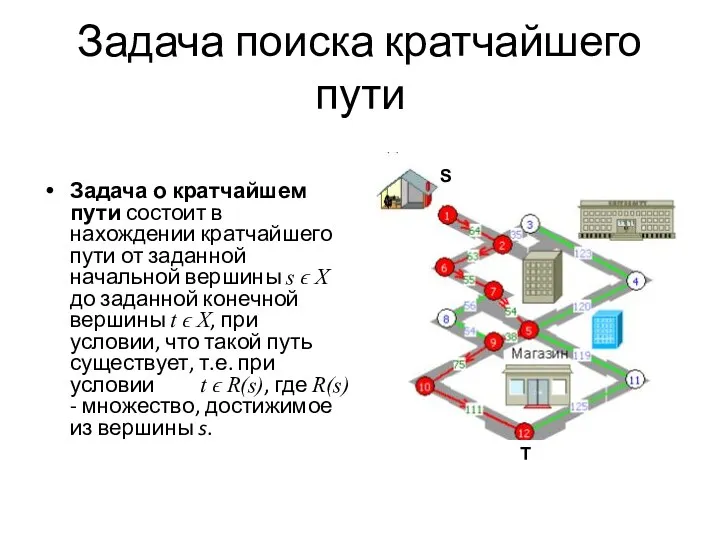
- 33. Задача поиска кратчайшего пути Задача о кратчайшем пути состоит в нахождении кратчайшего пути от заданной начальной
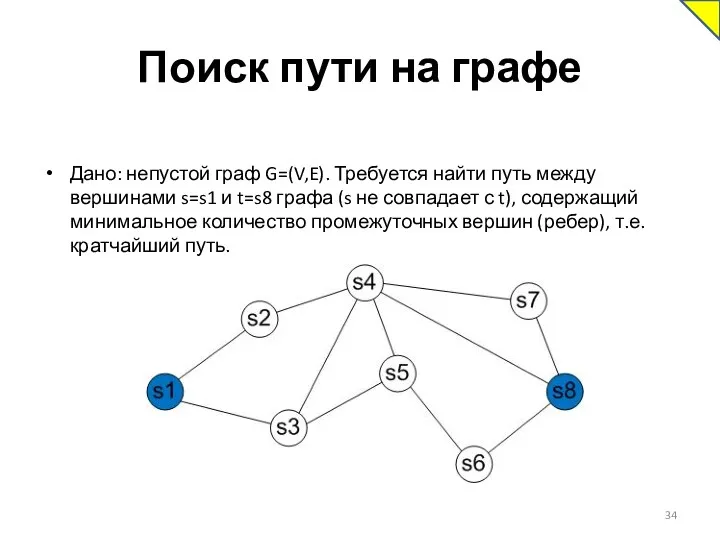
- 34. Поиск пути на графе Дано: непустой граф G=(V,E). Требуется найти путь между вершинами s=s1 и t=s8
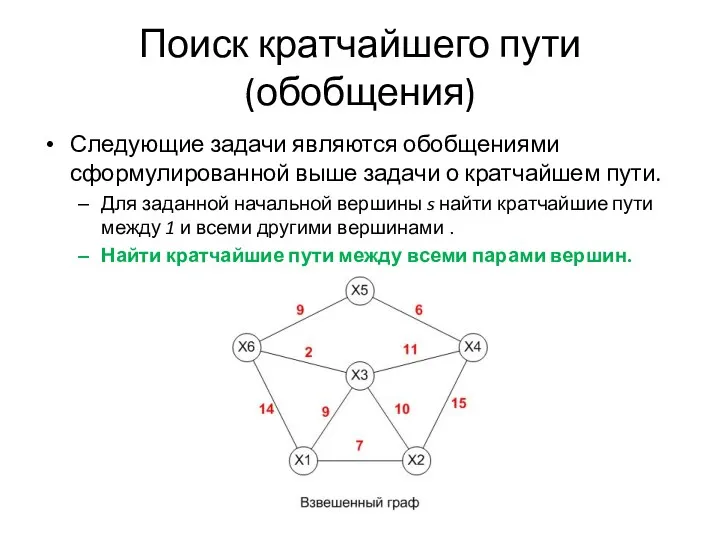
- 35. Поиск кратчайшего пути (обобщения) Следующие задачи являются обобщениями сформулированной выше задачи о кратчайшем пути. Для заданной
- 36. Наиболее известные алгоритмы поиска кратчайшего пути алгоритм Дейкстры; алгоритм Белмана-Форда; переборные алгоритмы волновой алгоритм.
- 37. Алгоритм Дейкстры Алгоритм Дейкстры Шаг 1. Всем вершинам, за исключением первой, присваивается вес равный бесконечности, а
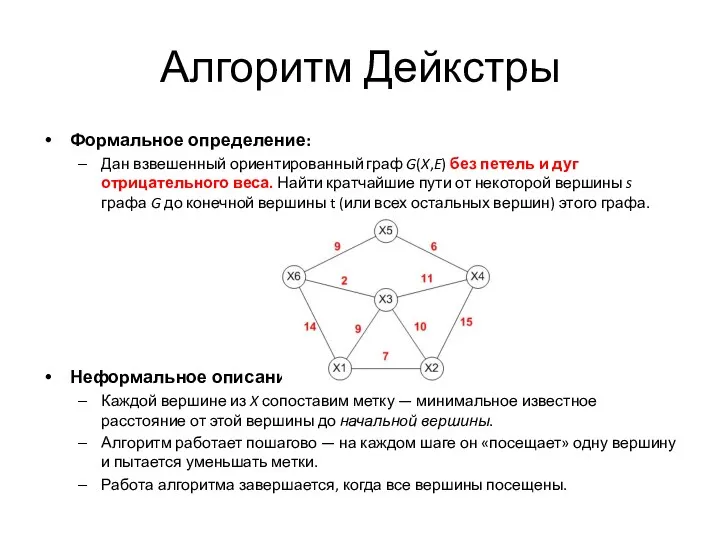
- 38. Алгоритм Дейкстры Формальное определение: Дан взвешенный ориентированный граф G(X,E) без петель и дуг отрицательного веса. Найти
- 39. Алгоритм Дейкстры Шаг алгоритма: Если все вершины посещены, алгоритм завершается. Иначе: из ещё не посещённых вершин
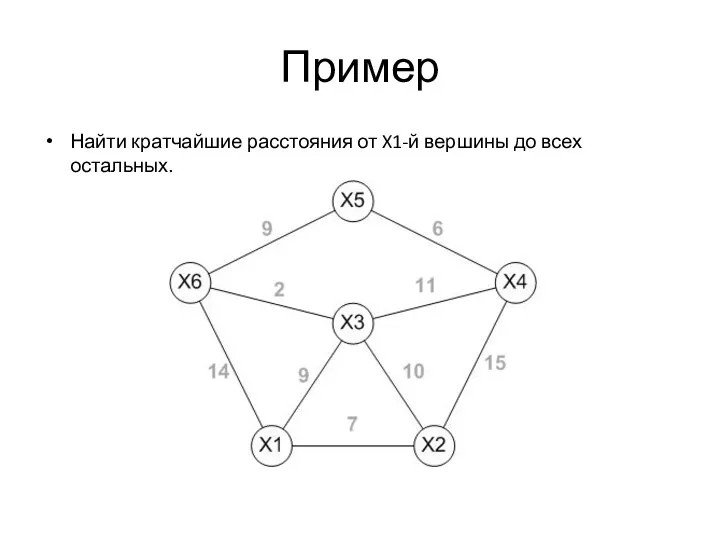
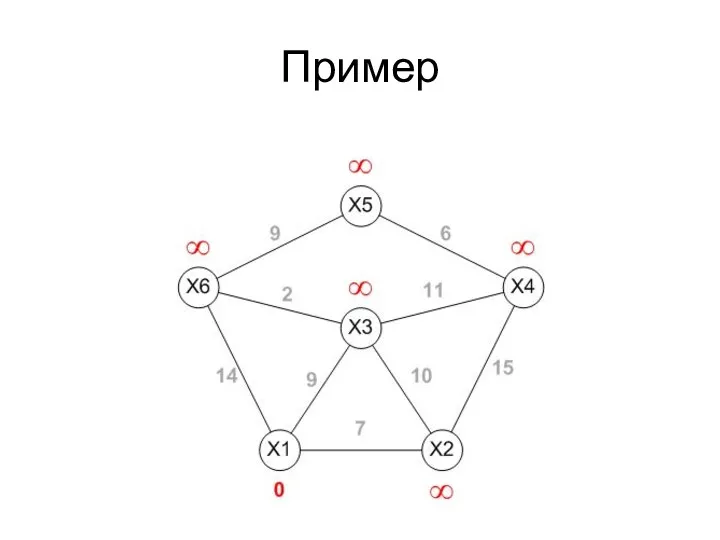
- 40. Пример Найти кратчайшие расстояния от X1-й вершины до всех остальных.
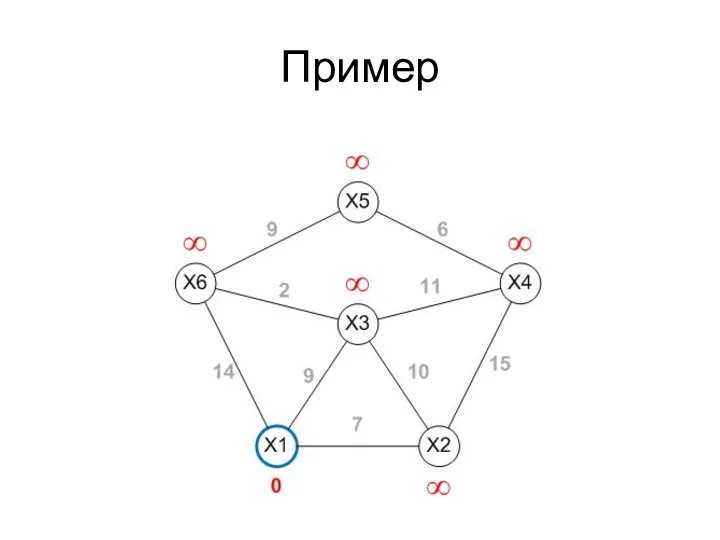
- 41. Пример
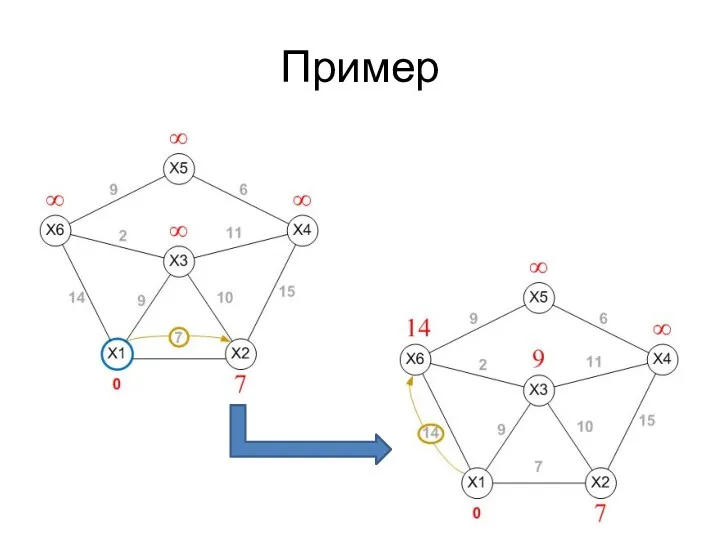
- 42. Пример
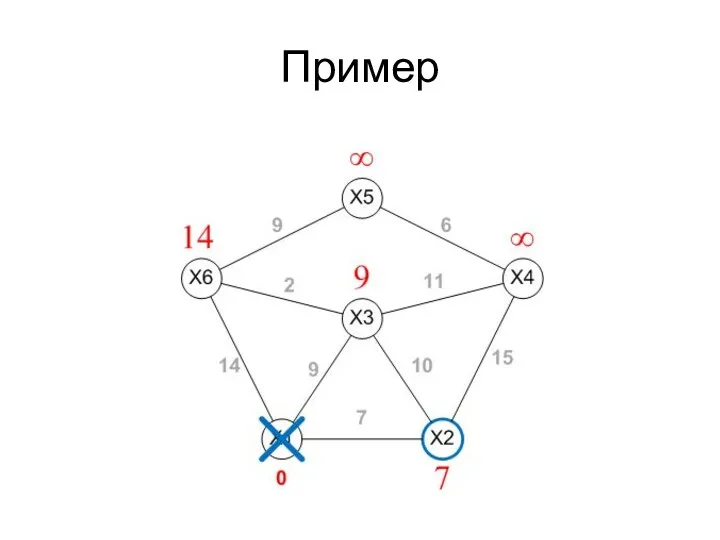
- 43. Пример
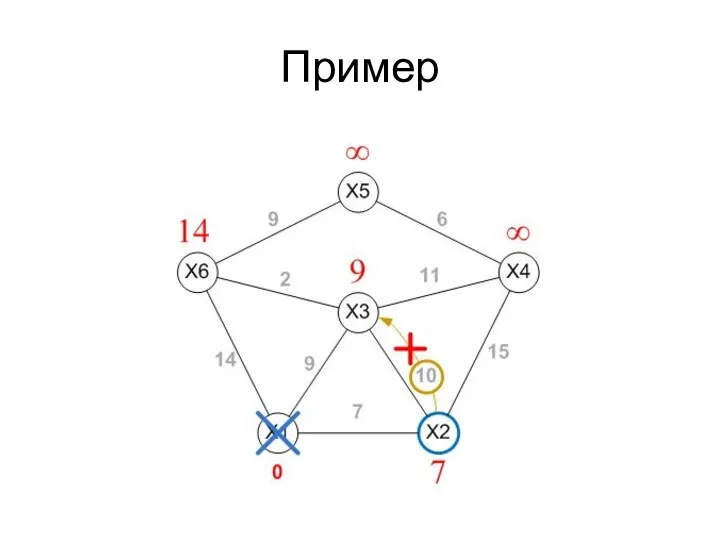
- 44. Пример
- 45. Пример
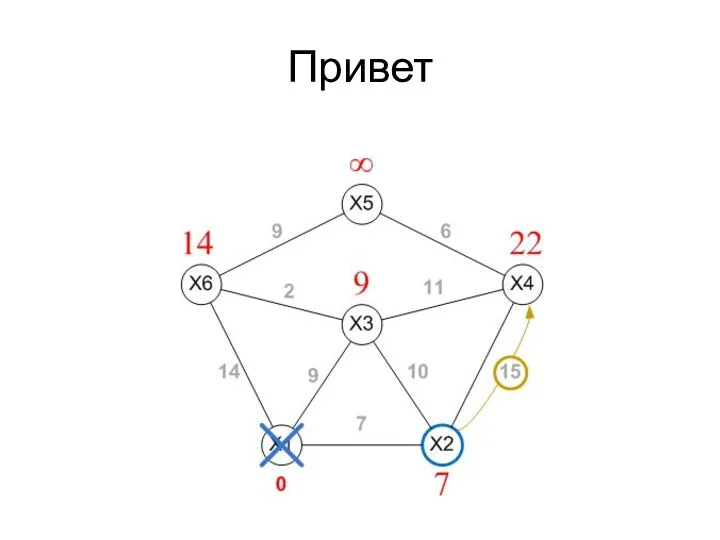
- 46. Привет
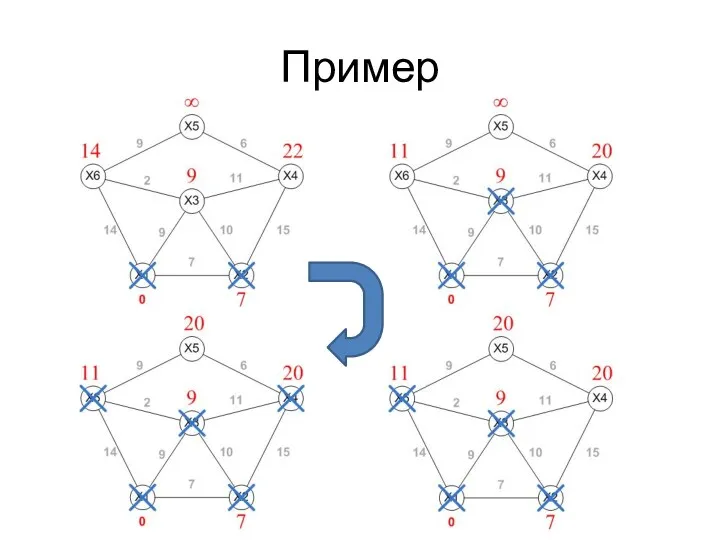
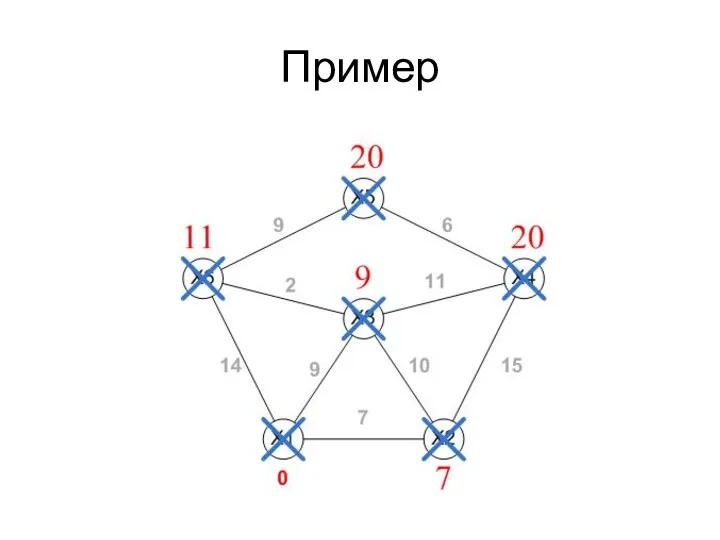
- 47. Пример
- 48. Пример
- 49. Применение алгоритмов поиска кратчайшего пути Вариант 1. Дана сеть автомобильных дорог, соединяющих города Московской области. Некоторые
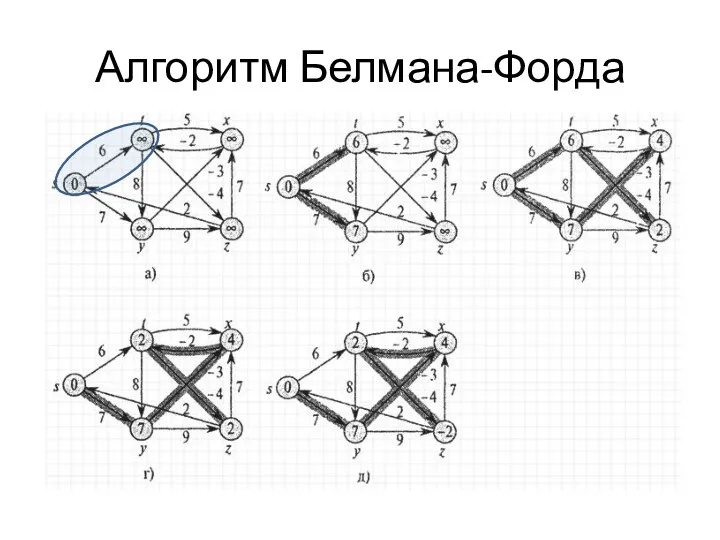
- 50. Алгоритм Белмана-Форда
- 51. Алгоритм Беллмана-Форда Дан ориентированный или неориентированный граф G со взвешенными рёбрами. Длиной пути назовём сумму весов
- 52. Алгоритм Белмана-Форда
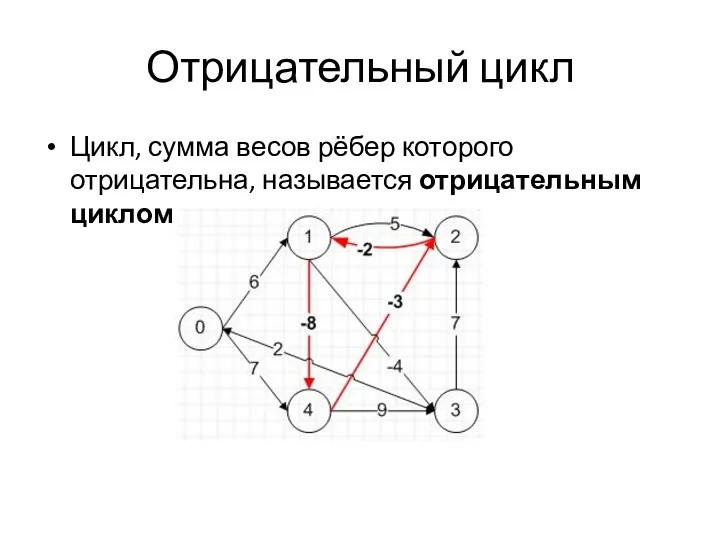
- 53. Отрицательный цикл Цикл, сумма весов рёбер которого отрицательна, называется отрицательным циклом.
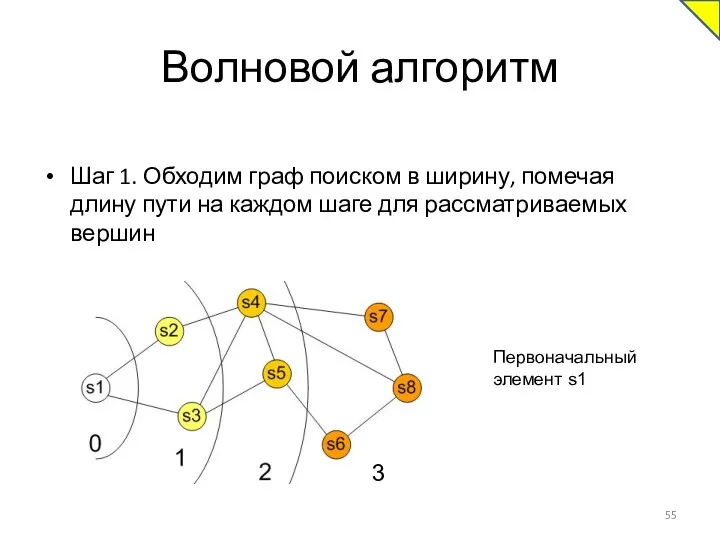
- 54. Волновой алгоритм
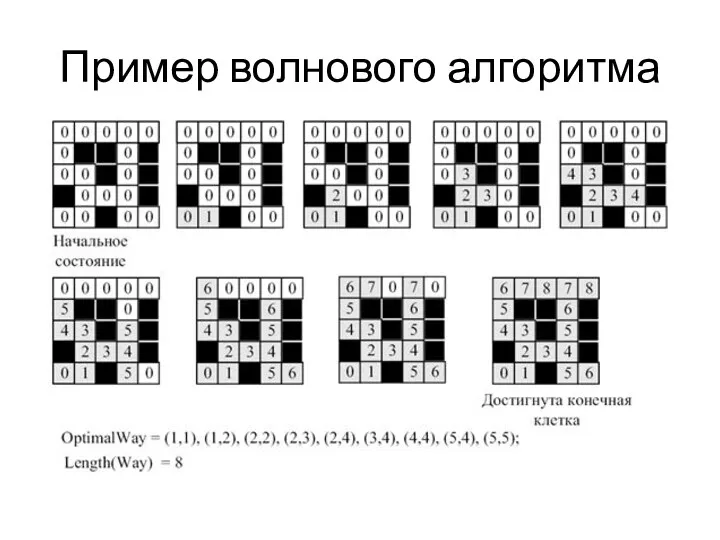
- 55. Волновой алгоритм Шаг 1. Обходим граф поиском в ширину, помечая длину пути на каждом шаге для
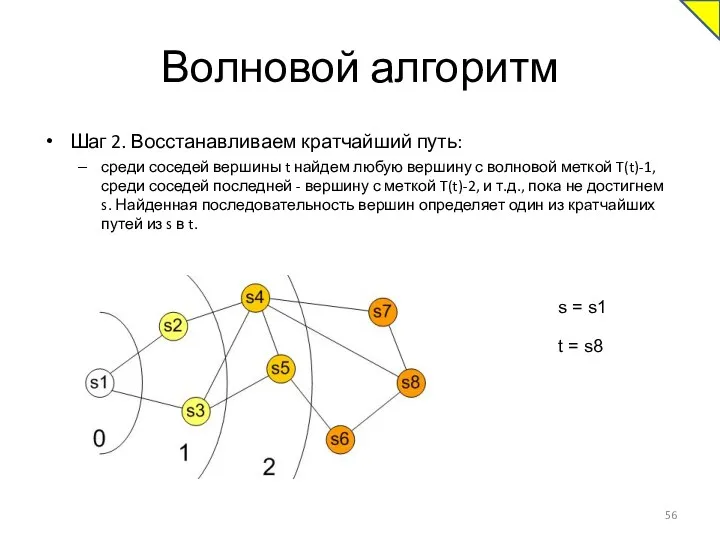
- 56. Волновой алгоритм Шаг 2. Восстанавливаем кратчайший путь: среди соседей вершины t найдем любую вершину с волновой
- 57. Пример волнового алгоритма
- 58. Применение методов поиска кратчайшего пути
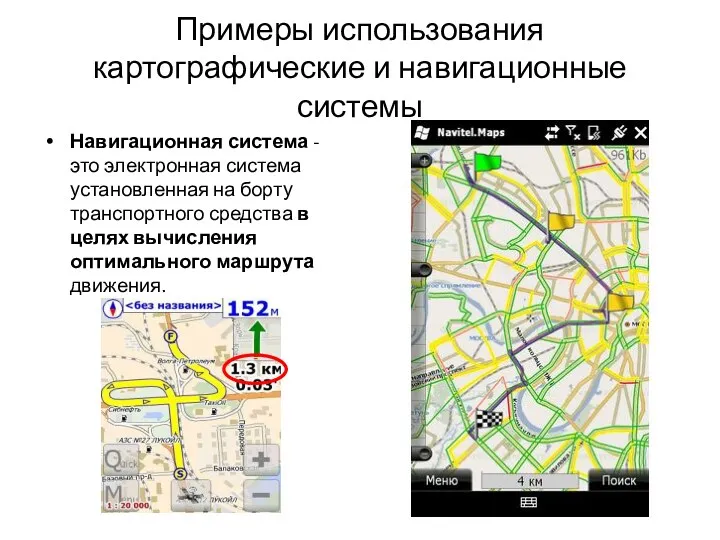
- 59. Примеры использования картографические и навигационные системы Навигационная система - это электронная система установленная на борту транспортного
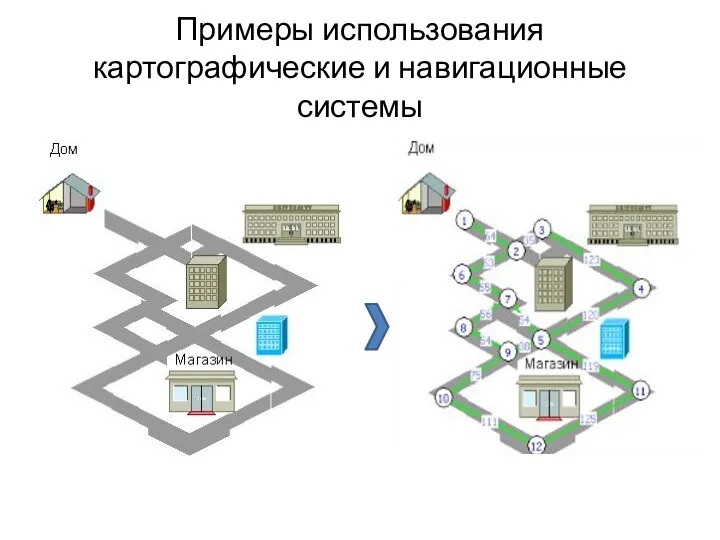
- 60. Примеры использования картографические и навигационные системы
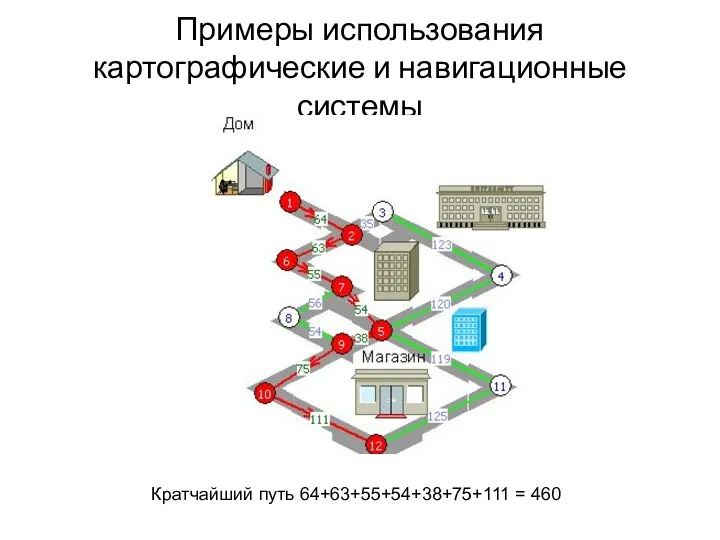
- 61. Примеры использования картографические и навигационные системы Кратчайший путь 64+63+55+54+38+75+111 = 460
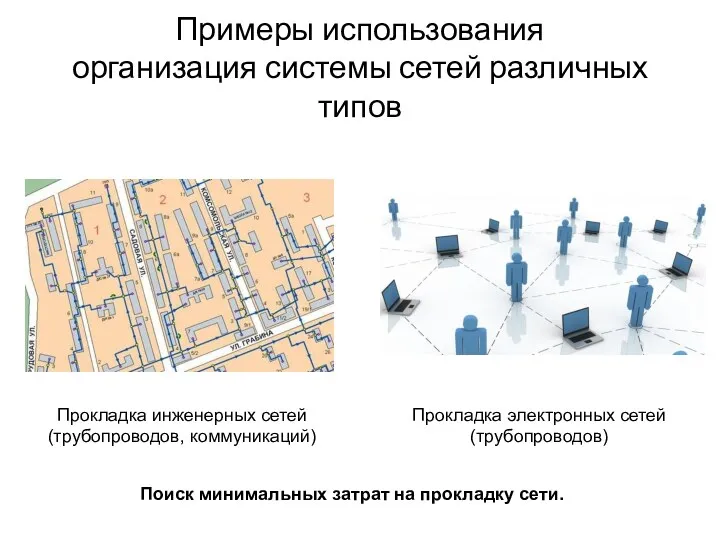
- 62. Примеры использования организация системы сетей различных типов Прокладка инженерных сетей (трубопроводов, коммуникаций) Прокладка электронных сетей (трубопроводов)
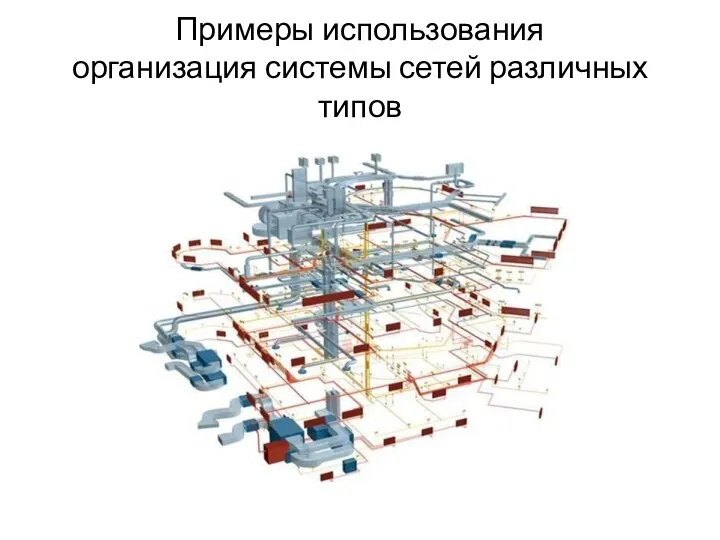
- 63. Примеры использования организация системы сетей различных типов
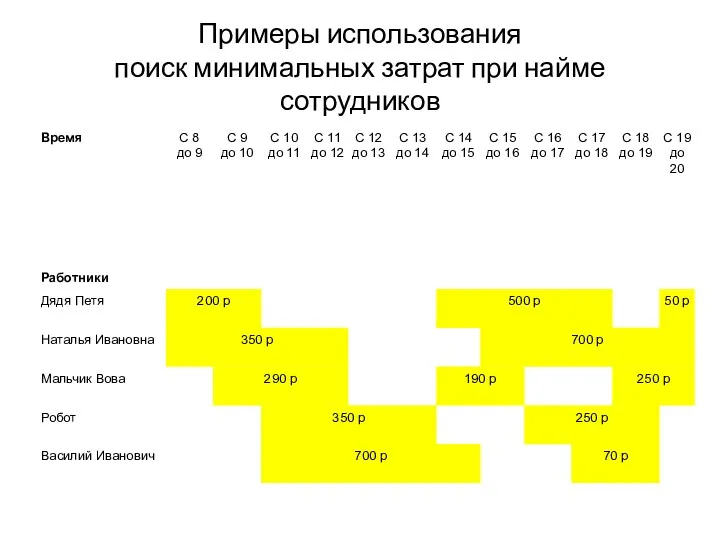
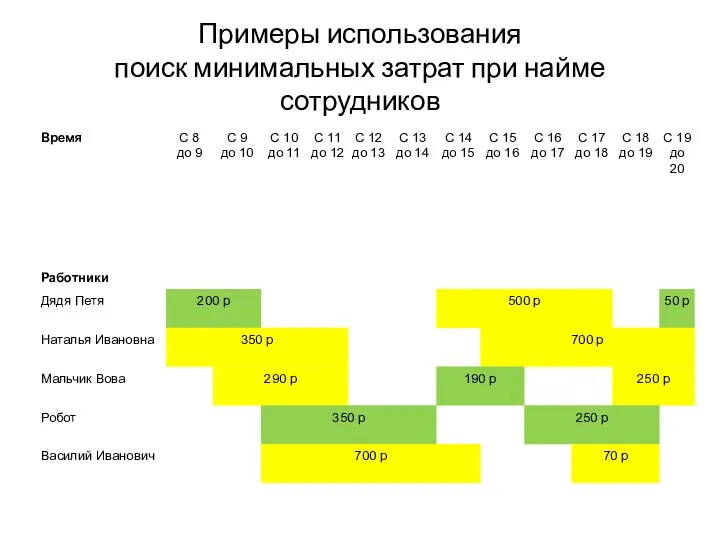
- 64. Примеры использования поиск минимальных затрат при найме сотрудников
- 65. Примеры использования поиск минимальных затрат при найме сотрудников
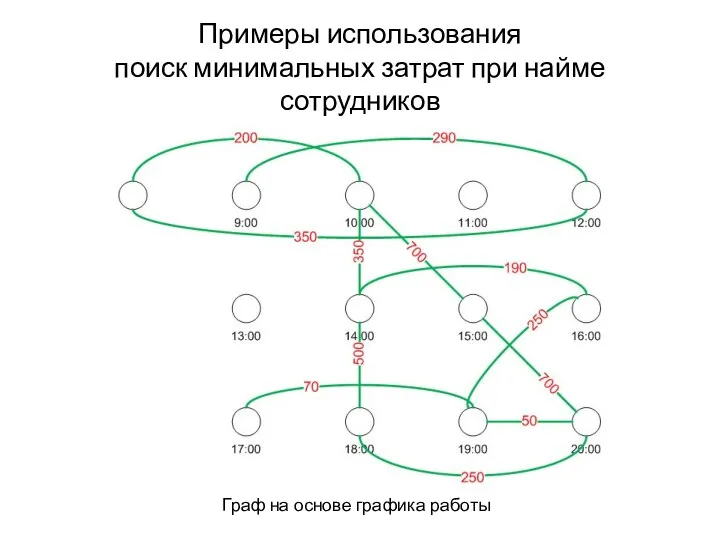
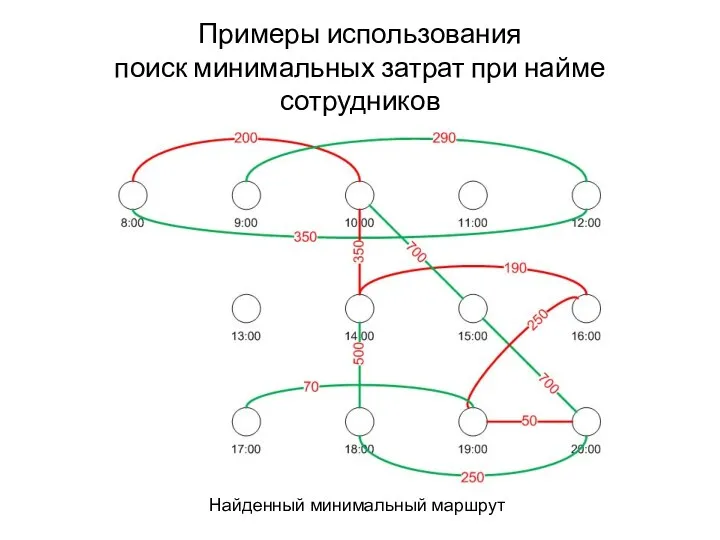
- 66. Примеры использования поиск минимальных затрат при найме сотрудников Граф на основе графика работы
- 67. Примеры использования поиск минимальных затрат при найме сотрудников Найденный минимальный маршрут
- 68. Примеры использования поиск минимальных затрат при найме сотрудников
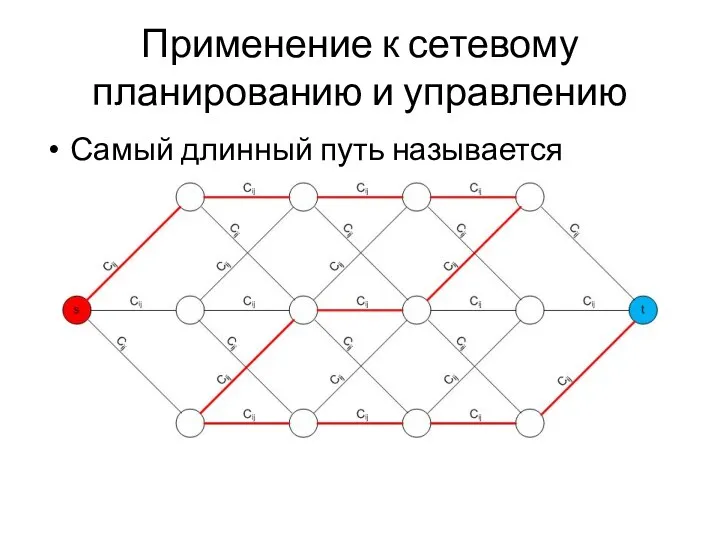
- 69. Применение к сетевому планированию и управлению Самый длинный путь называется критическим путем
- 70. Задача о максимальном потоке
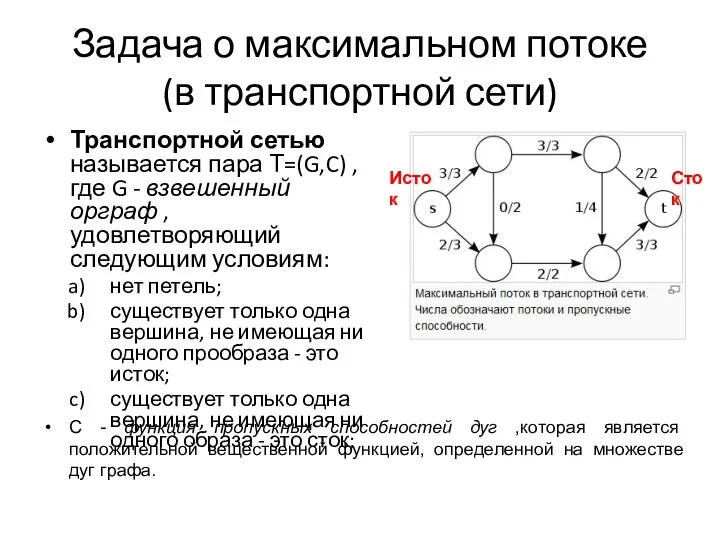
- 71. Задача о максимальном потоке (в транспортной сети) Транспортной сетью называется пара Т=(G,C) , где G -
- 72. Задача о максимальном потоке Потоком в транспортной сети Т называется неотрицательная вещественная функция, определенная на множестве
- 73. Алгоритм Форда-Фалкерсона (шаги 1-3) Перенумеровать все вершины сети произвольным образом, кроме истока и стока. Задать некоторый
- 74. Алгоритм Форда-Фалкерсона (шаги 4-5) Если в результате процедуры помечивания вершина-сток метки не получила, то текущий поток
- 75. Алгоритм Форда-Фалкерсона (схема нахождения К) Схема нахождения К: К = min{ К1;К2 }, где Для нахождения
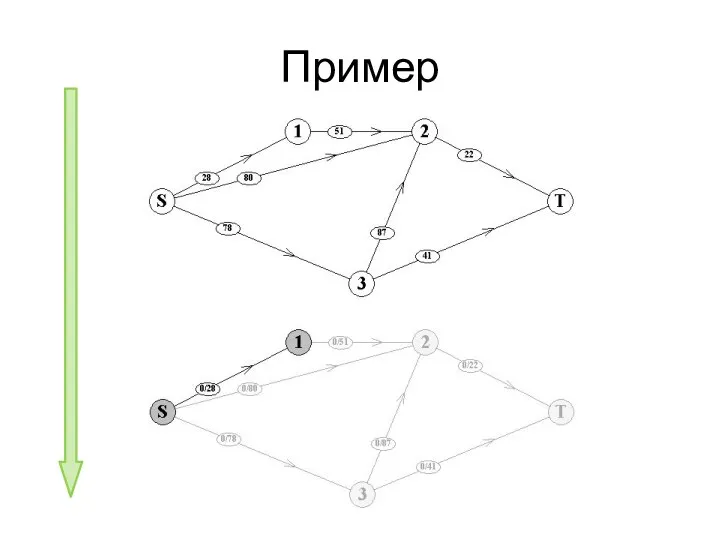
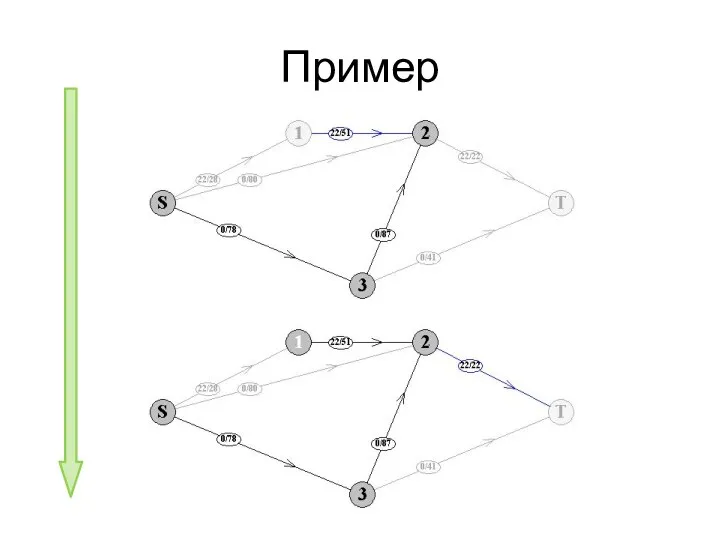
- 76. Пример
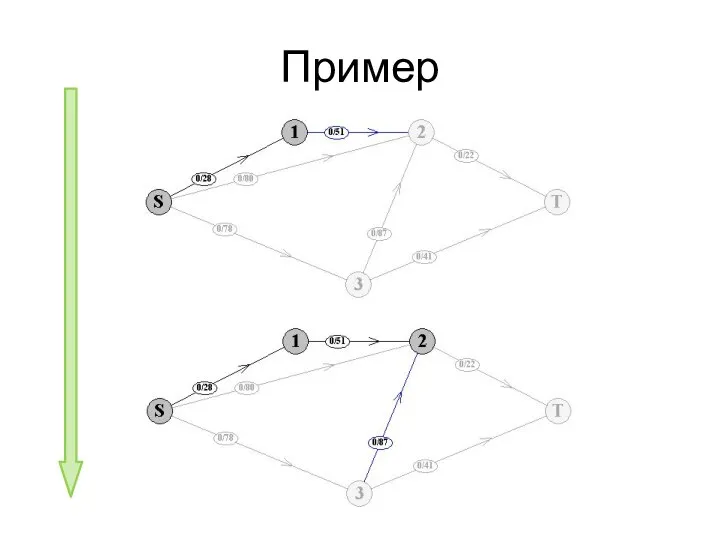
- 77. Пример
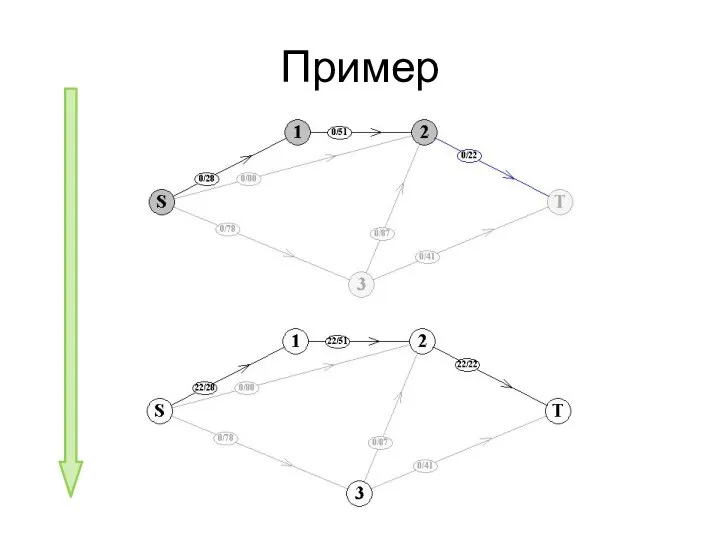
- 78. Пример
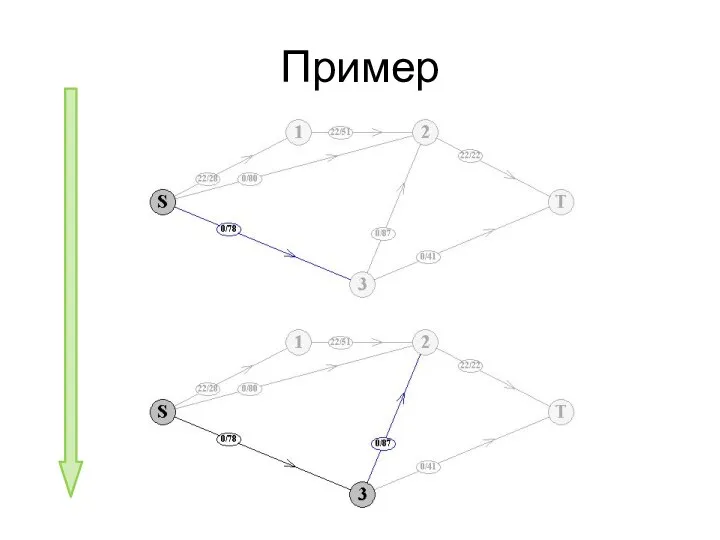
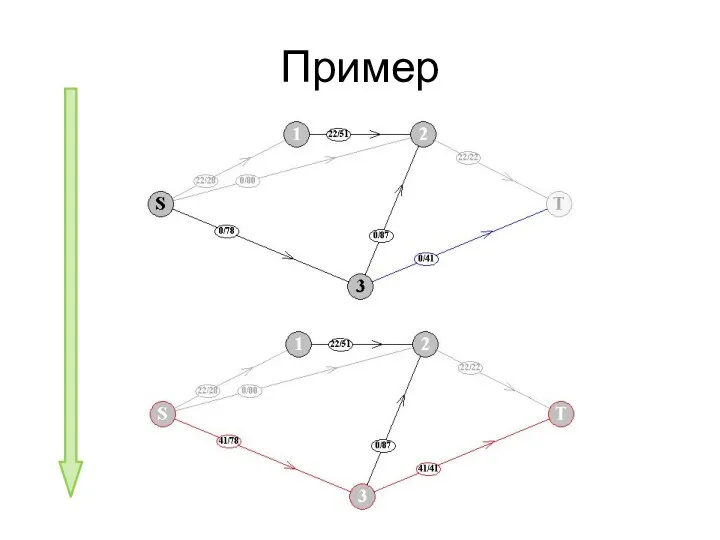
- 79. Пример
- 80. Пример
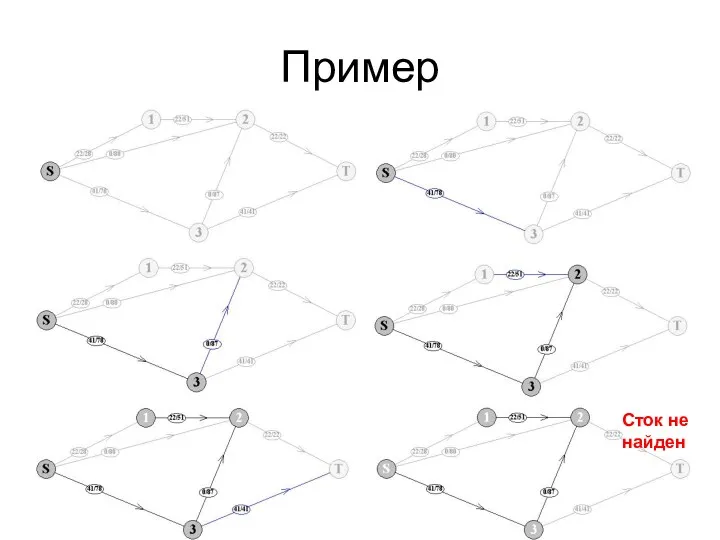
- 81. Пример
- 82. Пример Сток не найден
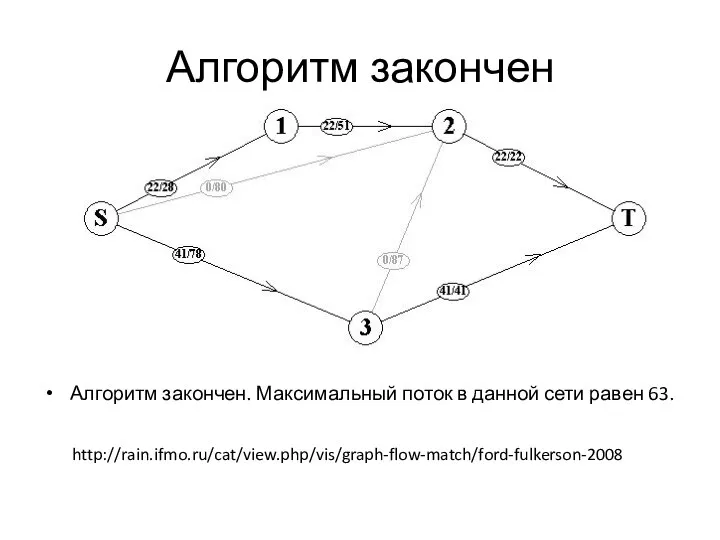
- 83. Алгоритм закончен Алгоритм закончен. Максимальный поток в данной сети равен 63. http://rain.ifmo.ru/cat/view.php/vis/graph-flow-match/ford-fulkerson-2008
- 84. Примеры использования задачи поиска максимального потока Пример 1. Расчет пропускной способности компьютерной или дорожной сети Пример
- 85. Пример 1 Расчет пропускной способности компьютерной или дорожной сети
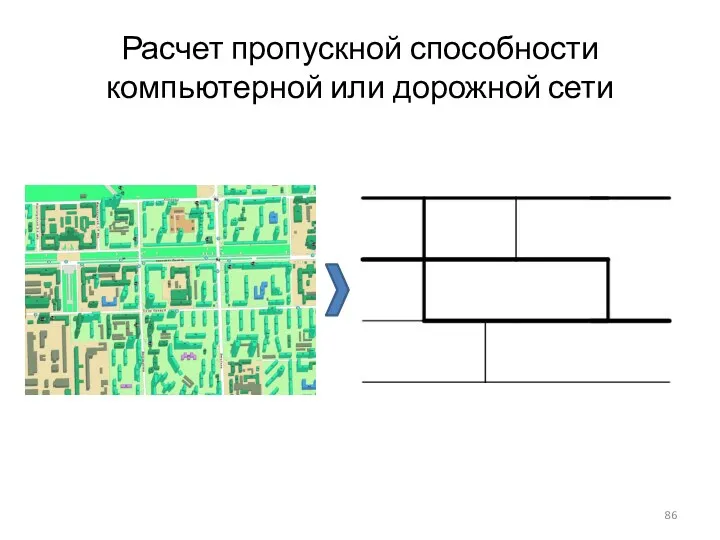
- 86. Расчет пропускной способности компьютерной или дорожной сети
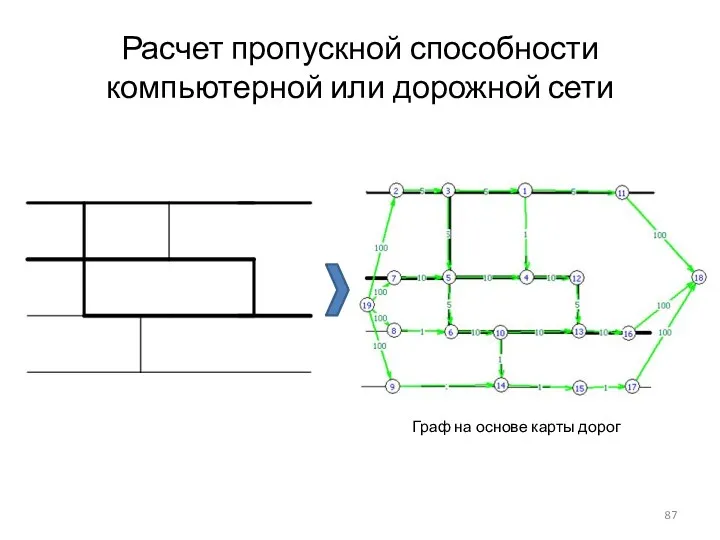
- 87. Расчет пропускной способности компьютерной или дорожной сети Граф на основе карты дорог
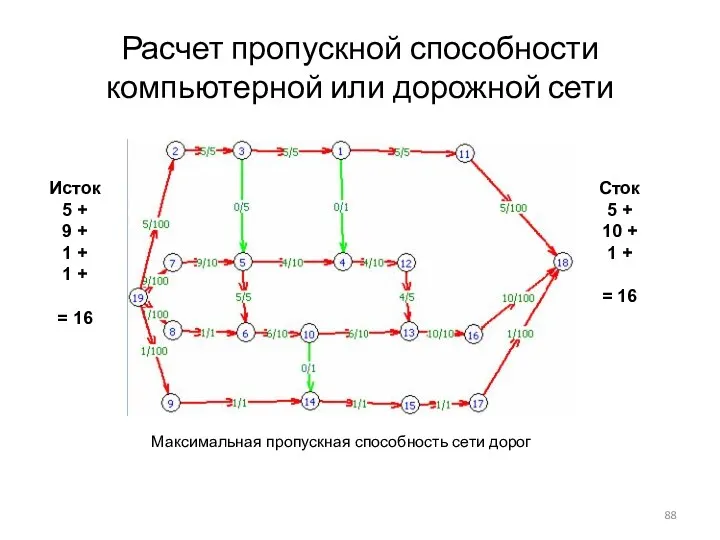
- 88. Расчет пропускной способности компьютерной или дорожной сети Максимальная пропускная способность сети дорог Исток 5 + 9
- 89. Пример 2 Распределение работы между несколькими работниками
- 90. Распределение работы между несколькими работниками
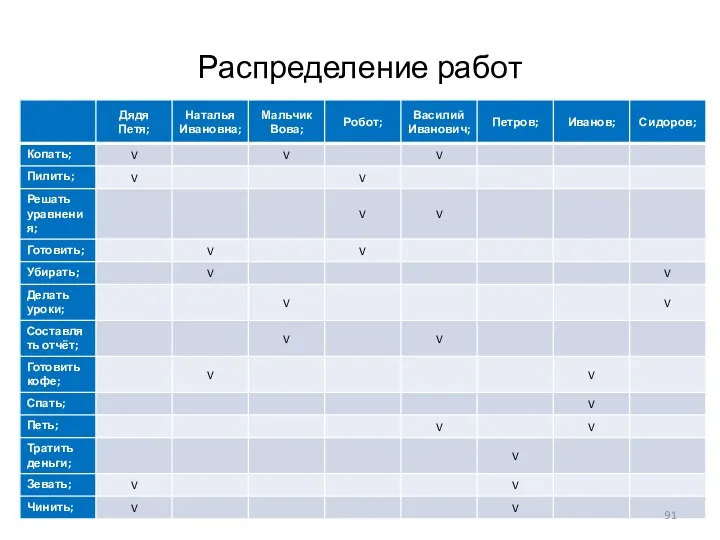
- 91. Распределение работ
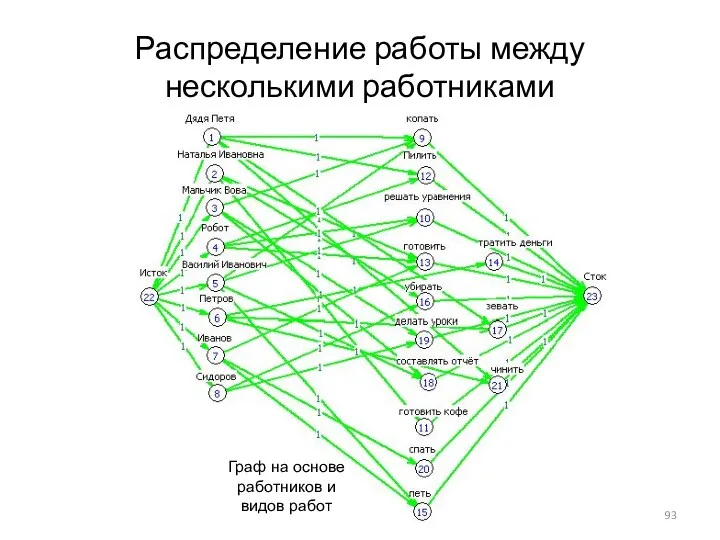
- 92. Распределение работы между несколькими работниками
- 93. Распределение работы между несколькими работниками Граф на основе работников и видов работ
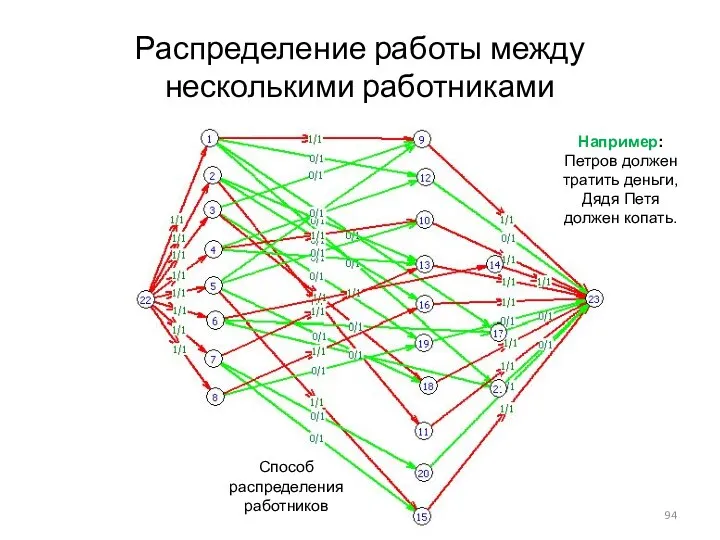
- 94. Распределение работы между несколькими работниками Способ распределения работников Например: Петров должен тратить деньги, Дядя Петя должен
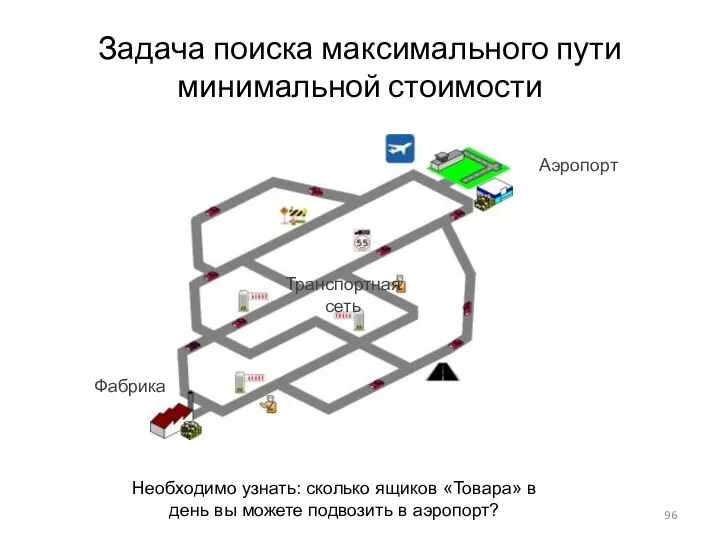
- 95. Пример 3. Задача поиска максимального пути минимальной стоимости
- 96. Задача поиска максимального пути минимальной стоимости Необходимо узнать: сколько ящиков «Товара» в день вы можете подвозить
- 97. Деревья Деревья Остовные деревья (остовы) Задача поиска минимального остовного дерева Алгоритмы
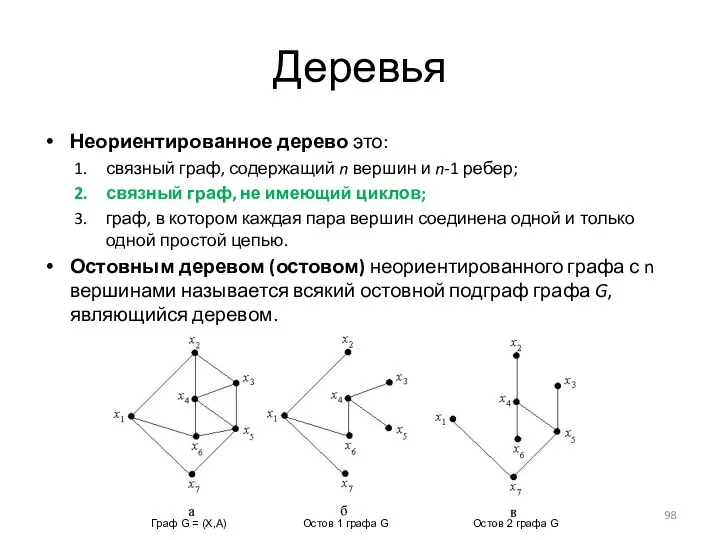
- 98. Деревья Неориентированное дерево это: связный граф, содержащий n вершин и n-1 ребер; связный граф, не имеющий
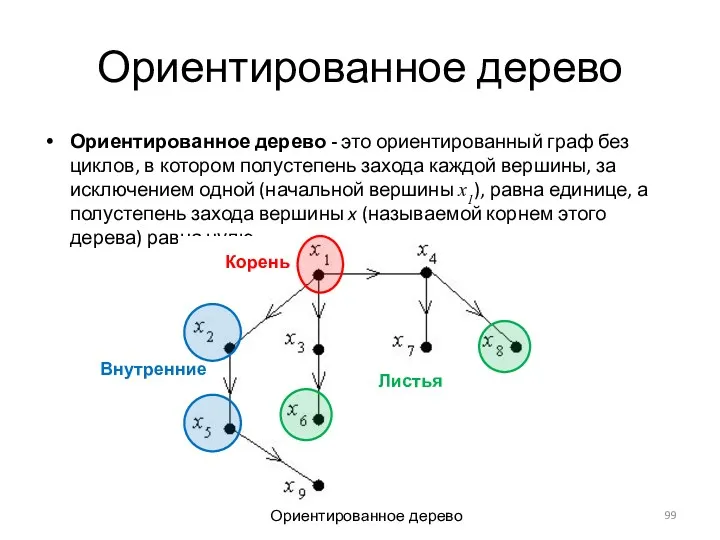
- 99. Ориентированное дерево Ориентированное дерево - это ориентированный граф без циклов, в котором полустепень захода каждой вершины,
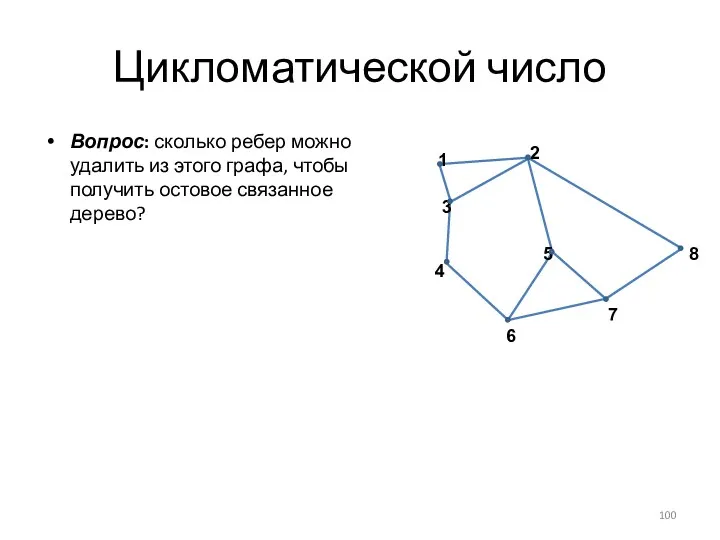
- 100. Цикломатической число Вопрос: сколько ребер можно удалить из этого графа, чтобы получить остовое связанное дерево?
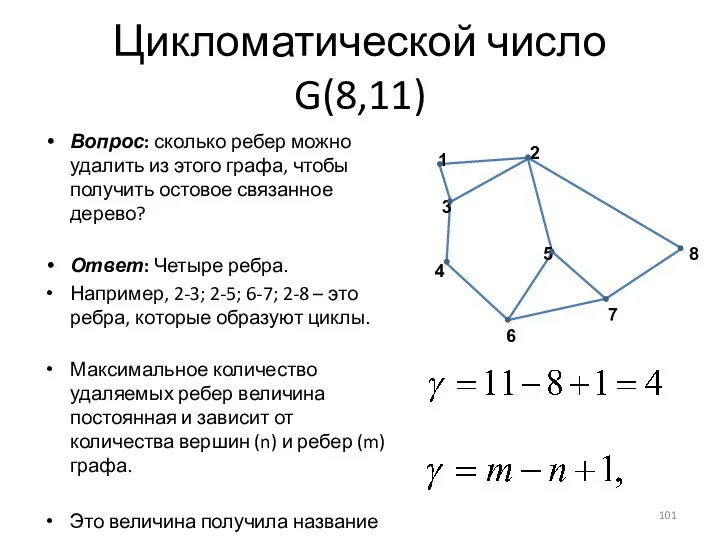
- 101. Цикломатической число G(8,11) Вопрос: сколько ребер можно удалить из этого графа, чтобы получить остовое связанное дерево?
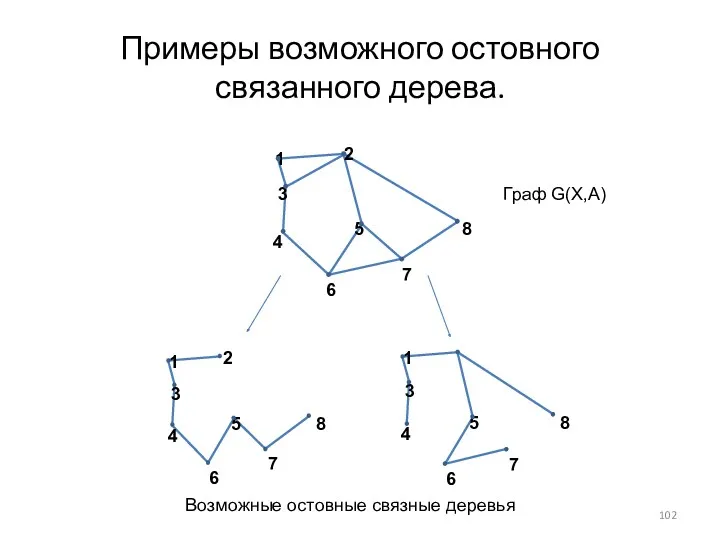
- 102. Примеры возможного остовного связанного дерева. Возможные остовные связные деревья Граф G(X,A)
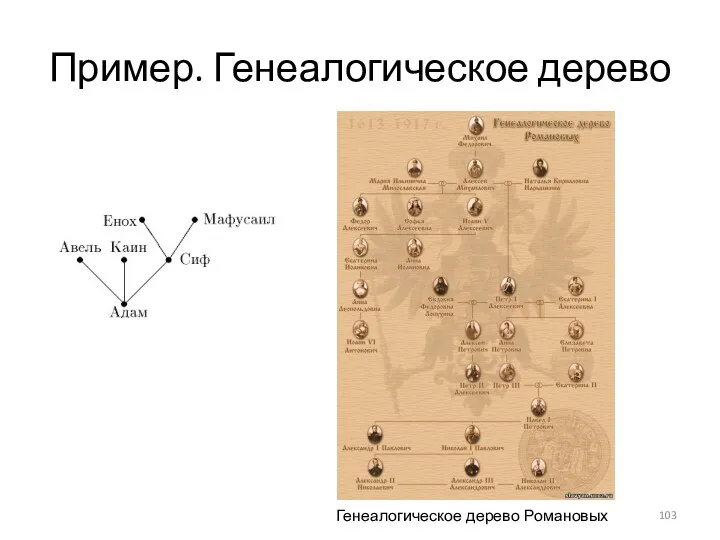
- 103. Пример. Генеалогическое дерево Генеалогическое дерево Романовых
- 104. Пример. Иерархические структуры Иерархическая структура управления в организациях
- 105. Задача поиска минимального остовного дерева (ПМОД)
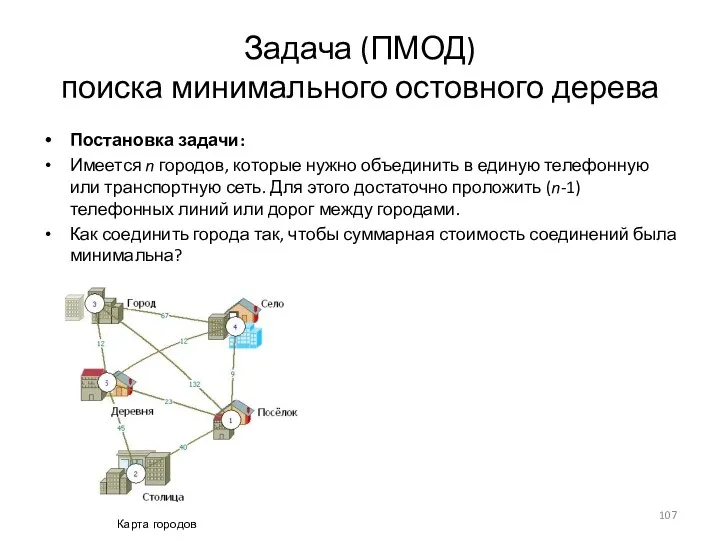
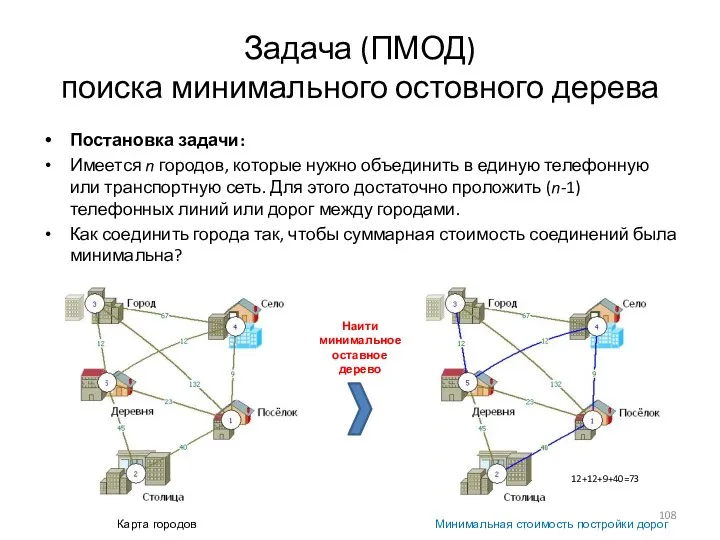
- 106. Задача (ПМОД) поиска минимального остовного дерева Постановка задачи: Имеется n городов, которые нужно объединить в единую
- 107. Задача (ПМОД) поиска минимального остовного дерева Постановка задачи: Имеется n городов, которые нужно объединить в единую
- 108. Задача (ПМОД) поиска минимального остовного дерева Постановка задачи: Имеется n городов, которые нужно объединить в единую
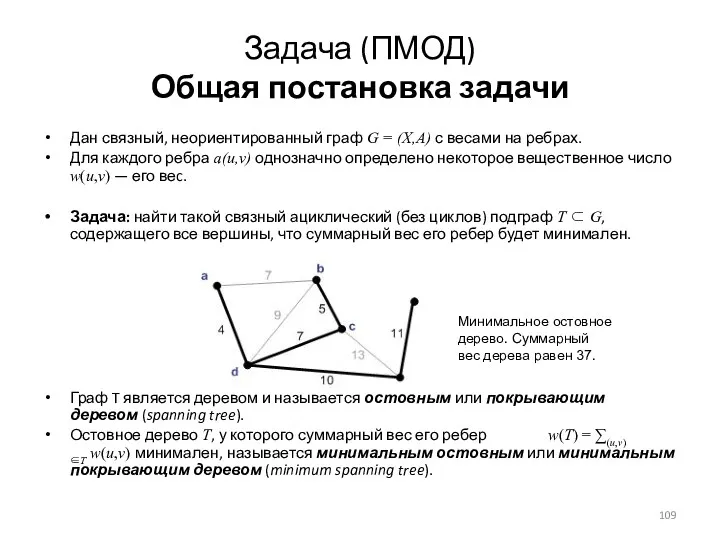
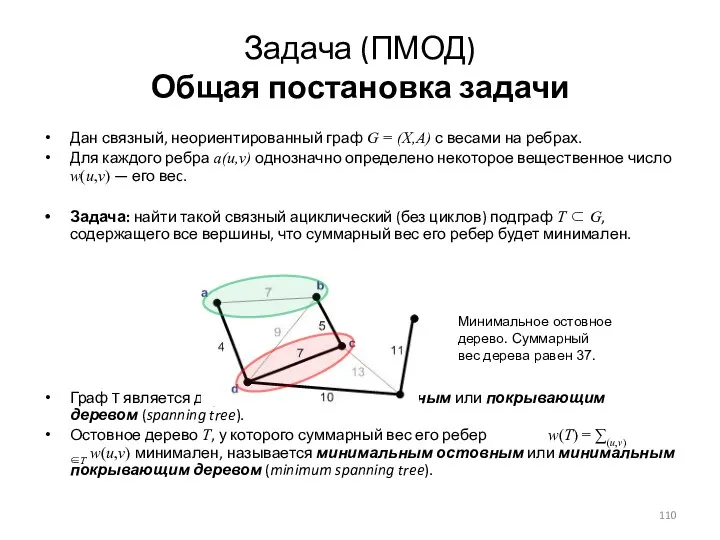
- 109. Задача (ПМОД) Общая постановка задачи Дан связный, неориентированный граф G = (X,A) с весами на ребрах.
- 110. Задача (ПМОД) Общая постановка задачи Дан связный, неориентированный граф G = (X,A) с весами на ребрах.
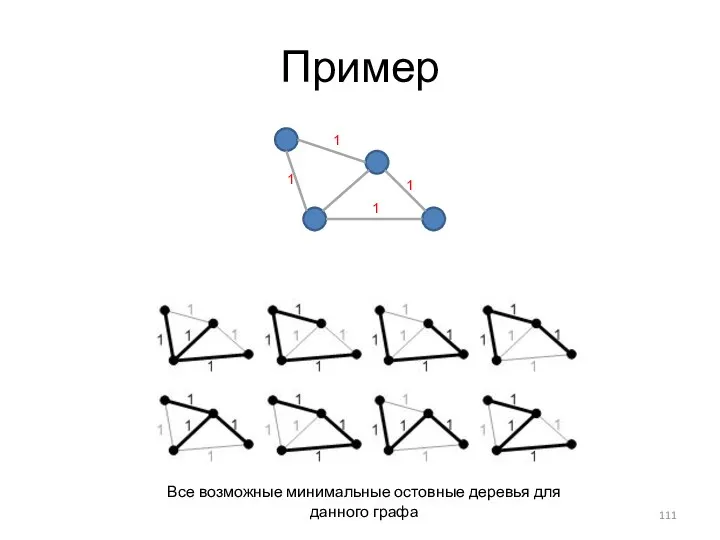
- 111. Пример Все возможные минимальные остовные деревья для данного графа
- 112. Задача (ПМОД) Алгоритмы решения Алгоритм Крускала Алгоритм Прима
- 113. Жадная стратегия Дан связный взвешенный неориентированный граф G(X,A) с n вершинами. Искомый остов строится постепенно. Алгоритм
- 114. Алгоритм Буровки
- 115. Вид возможной процедуры поиска безопасных ребер FIND-SAFE-EDGES(G) 1: foreach (для каждого) лидера x' 2: safe(x') ←
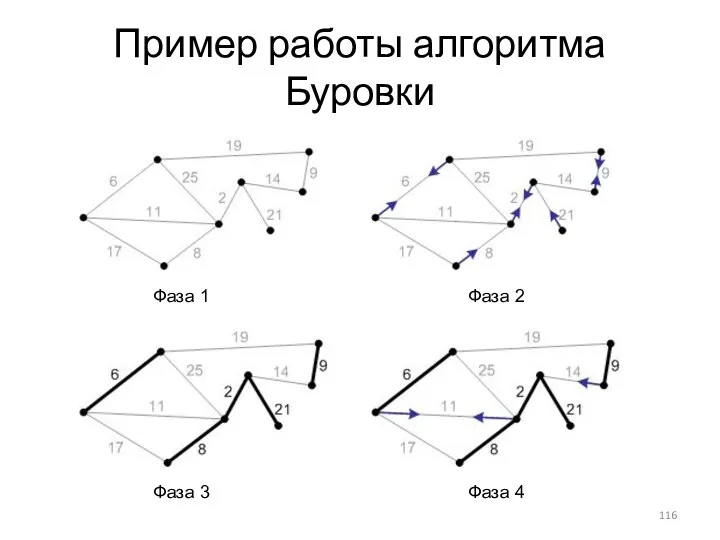
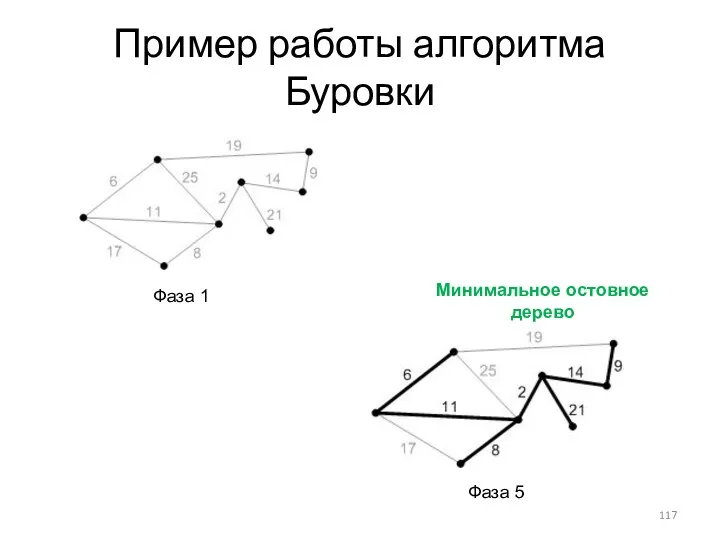
- 116. Пример работы алгоритма Буровки Фаза 1 Фаза 2 Фаза 3 Фаза 4
- 117. Пример работы алгоритма Буровки Фаза 1 Фаза 5 Минимальное остовное дерево
- 118. Алгоритм Крускала
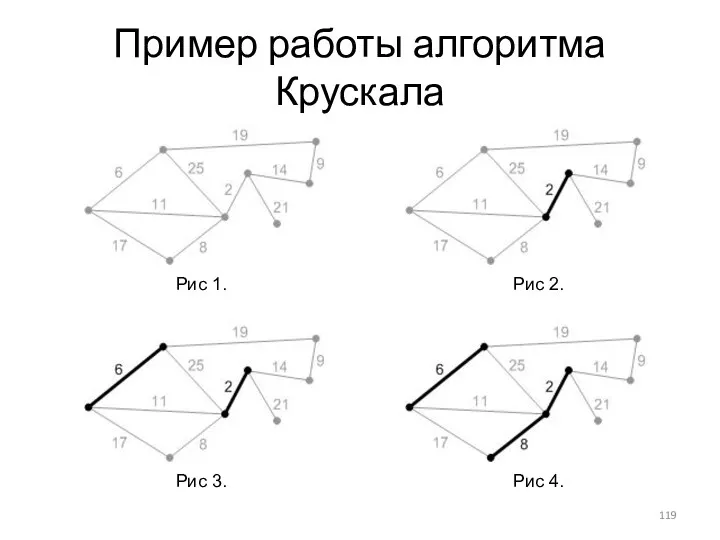
- 119. Пример работы алгоритма Крускала Рис 1. Рис 2. Рис 3. Рис 4.
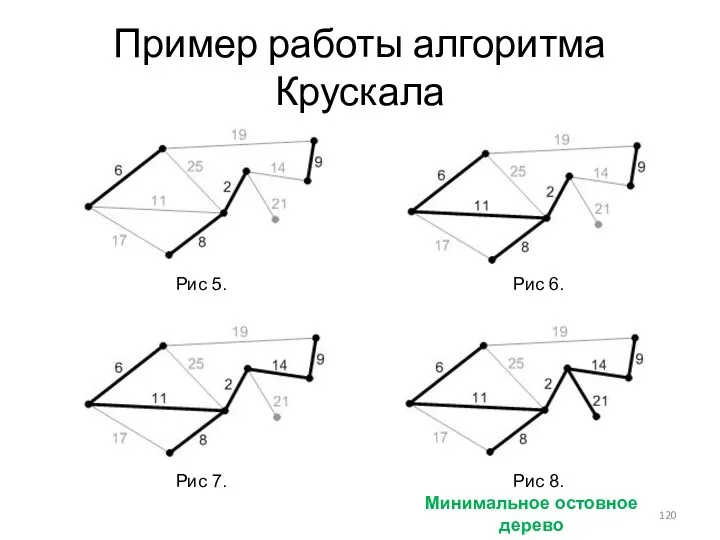
- 120. Пример работы алгоритма Крускала Рис 5. Рис 6. Рис 7. Рис 8. Минимальное остовное дерево
- 121. Алгоритм Крускала
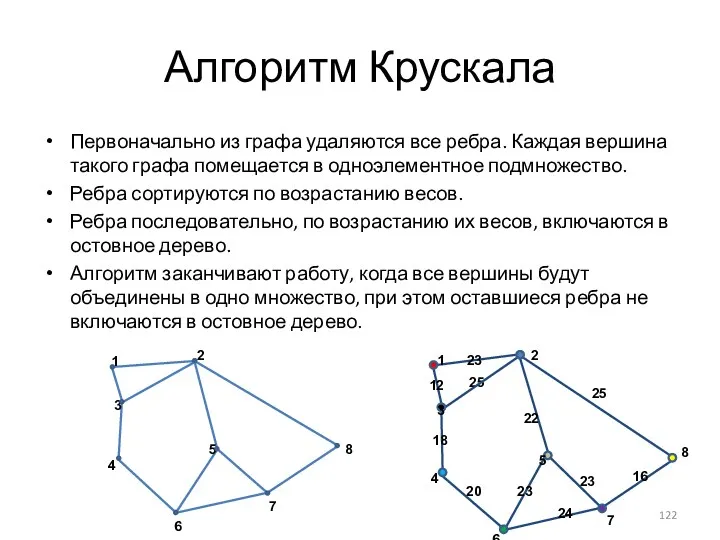
- 122. Алгоритм Крускала Первоначально из графа удаляются все ребра. Каждая вершина такого графа помещается в одноэлементное подмножество.
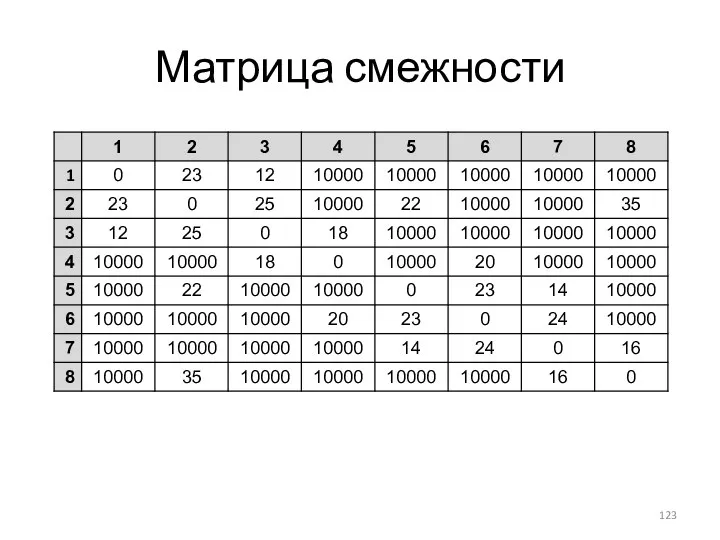
- 123. Матрица смежности
- 124. Алгоритм Крускала. Шаг 1. Раскрасить все вершины в разные цвета. Для этого создадим массив С(8).
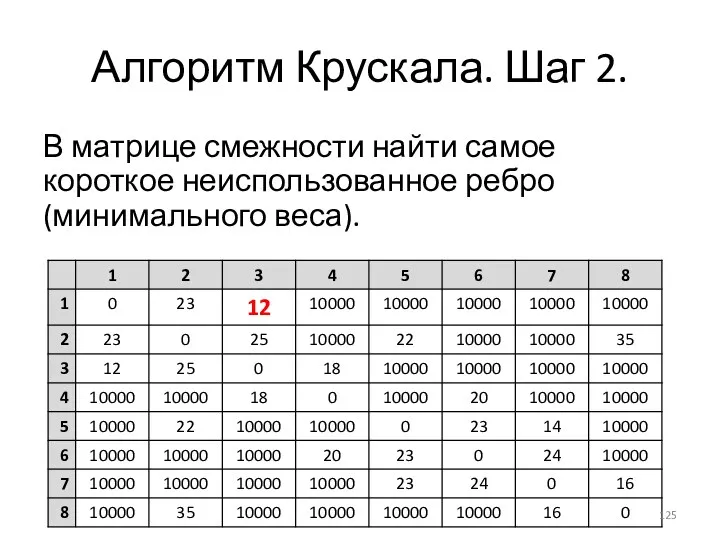
- 125. Алгоритм Крускала. Шаг 2. В матрице смежности найти самое короткое неиспользованное ребро (минимального веса).
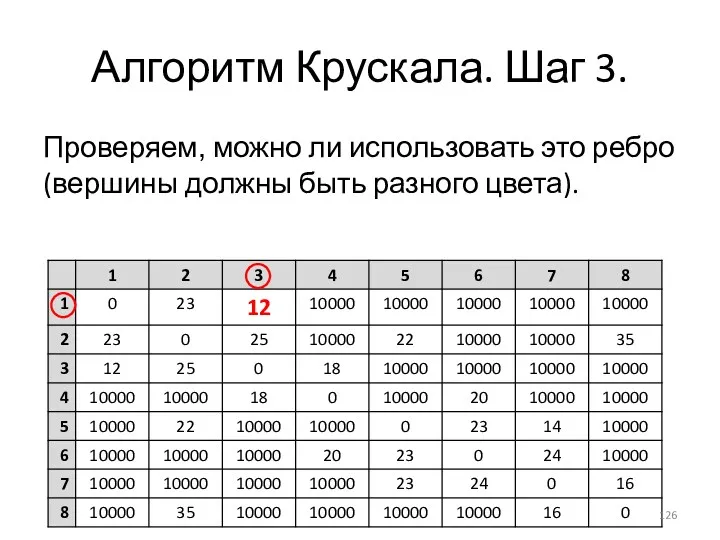
- 126. Алгоритм Крускала. Шаг 3. Проверяем, можно ли использовать это ребро (вершины должны быть разного цвета).
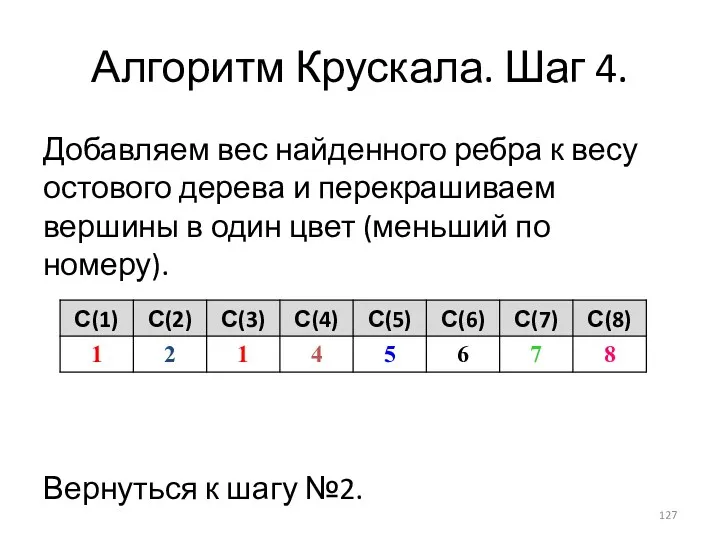
- 127. Алгоритм Крускала. Шаг 4. Добавляем вес найденного ребра к весу остового дерева и перекрашиваем вершины в
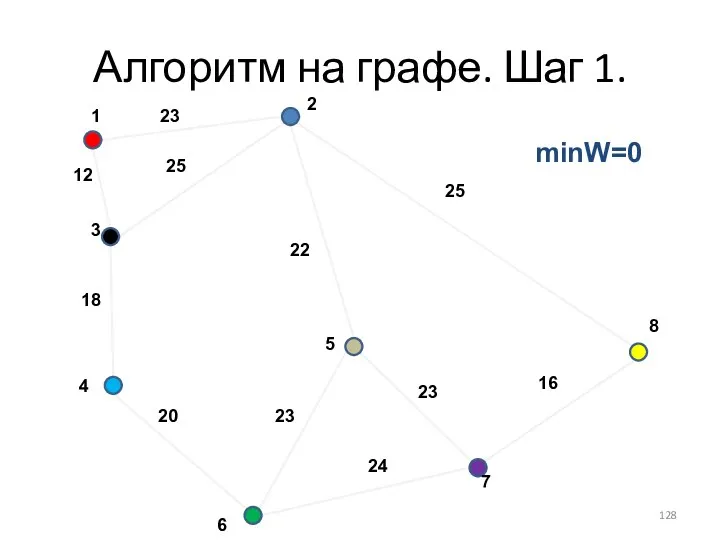
- 128. Алгоритм на графе. Шаг 1. minW=0
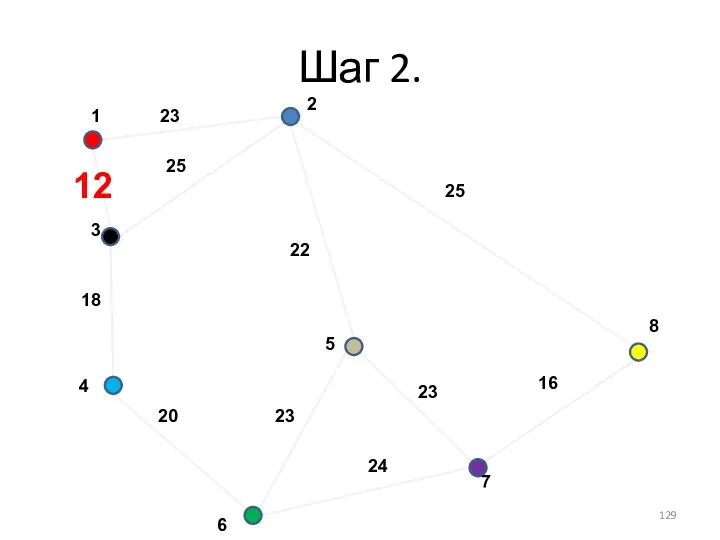
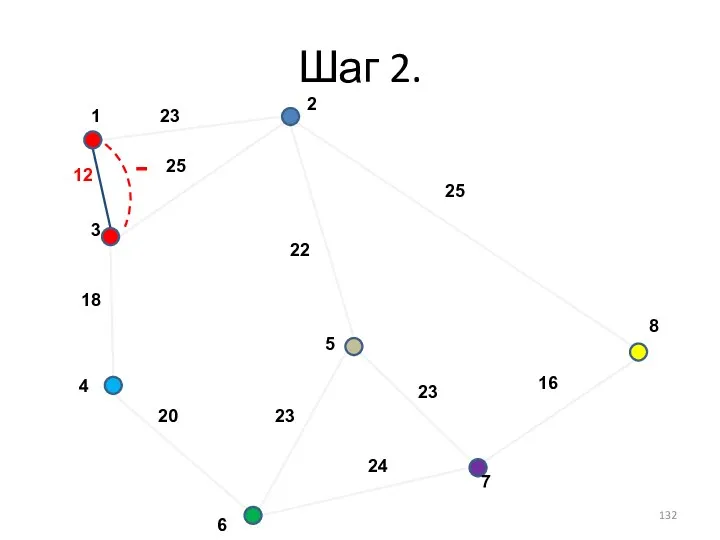
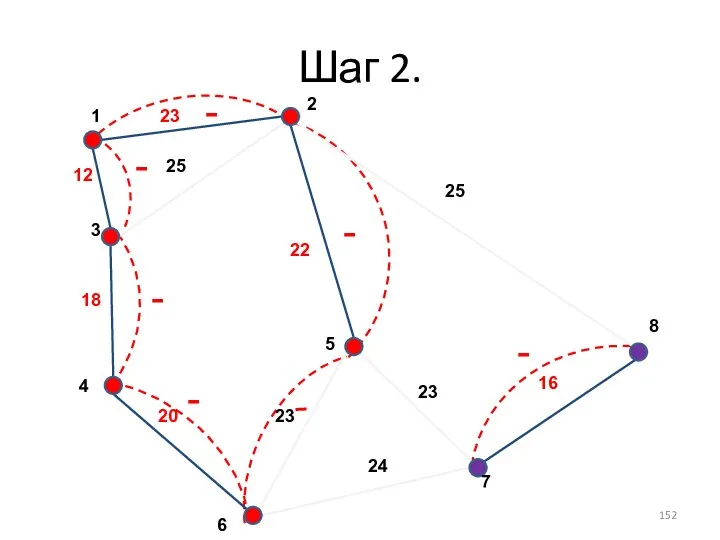
- 129. Шаг 2.
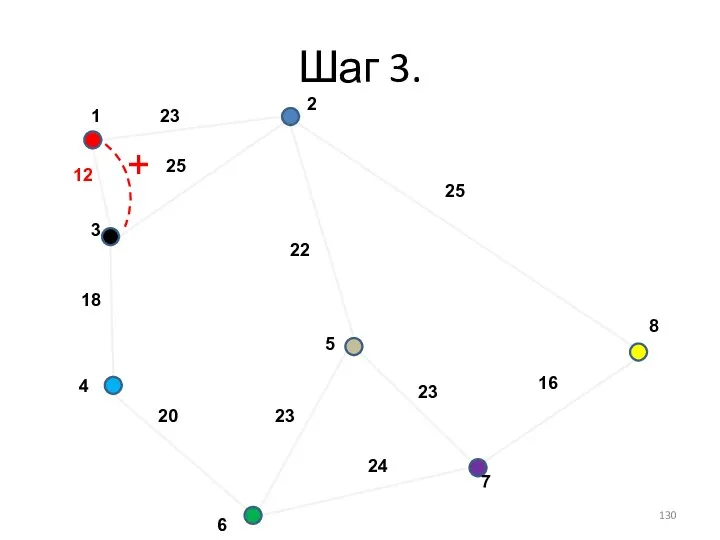
- 130. Шаг 3. +
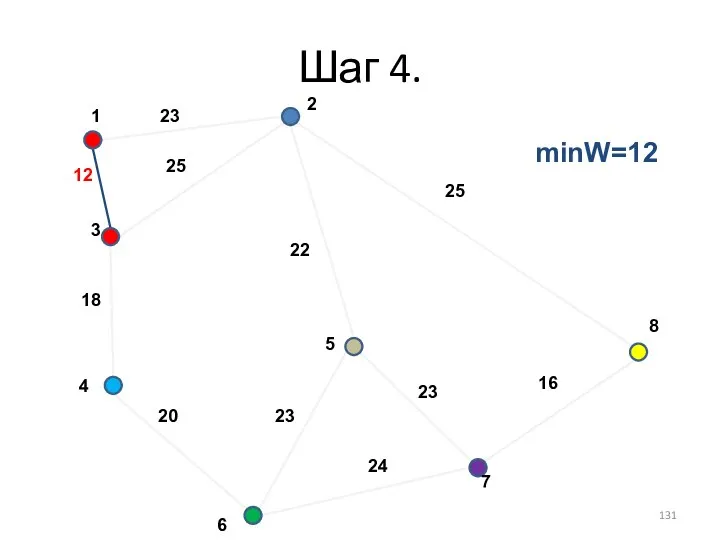
- 131. Шаг 4. minW=12
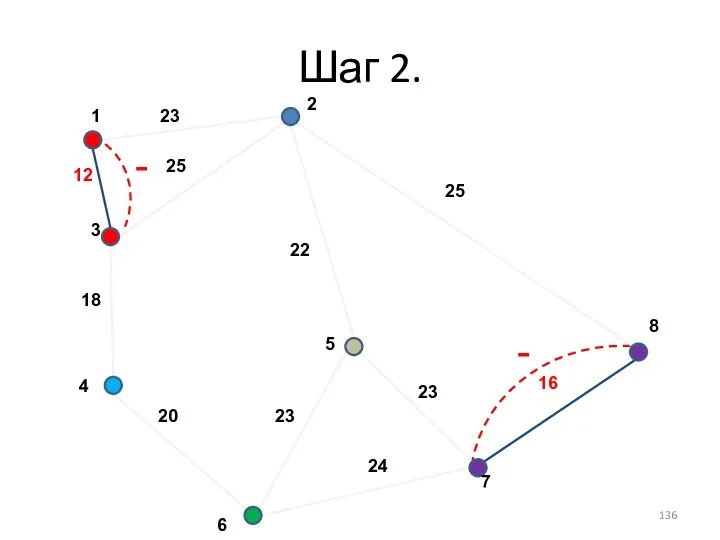
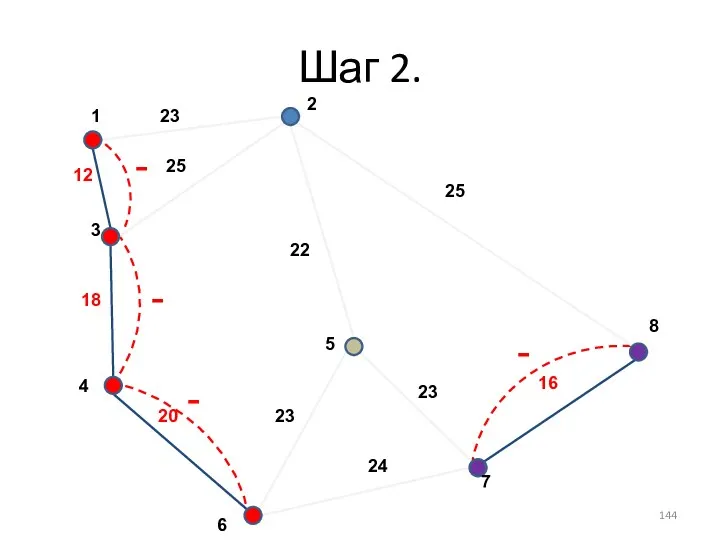
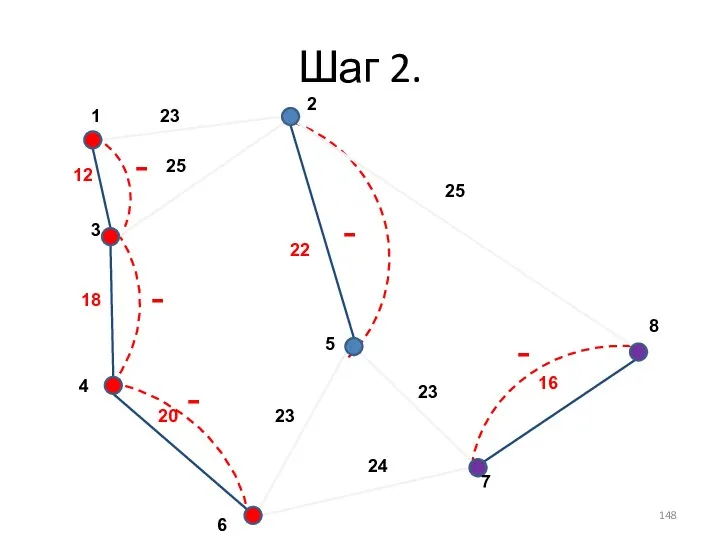
- 132. Шаг 2. -
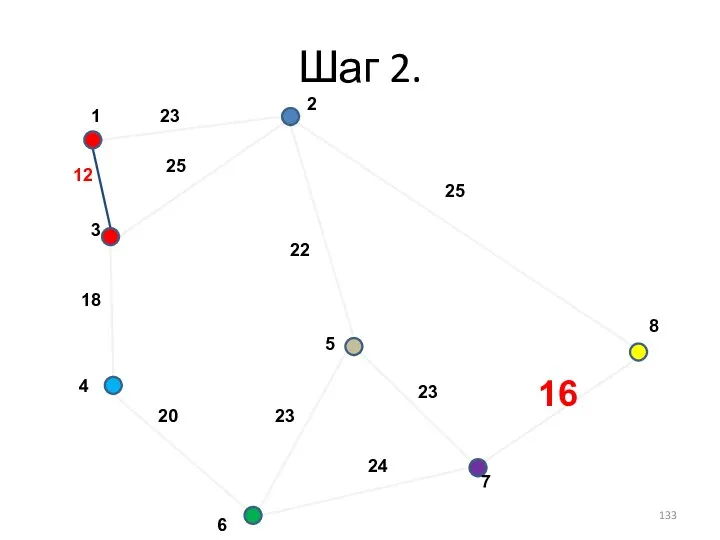
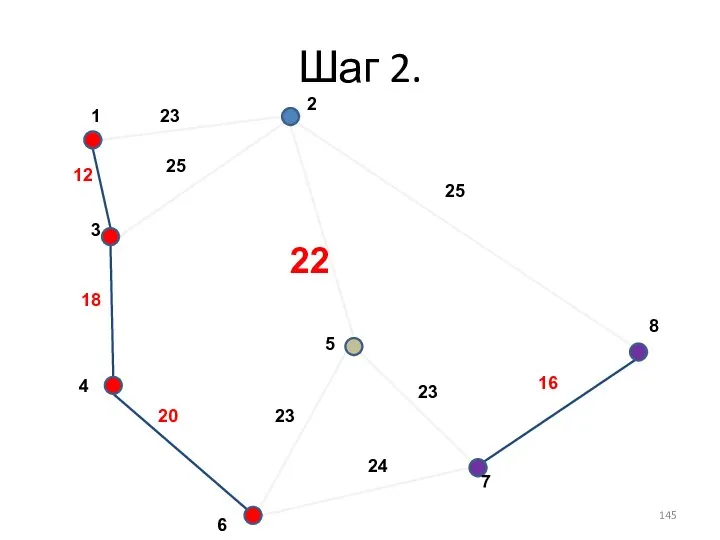
- 133. Шаг 2.
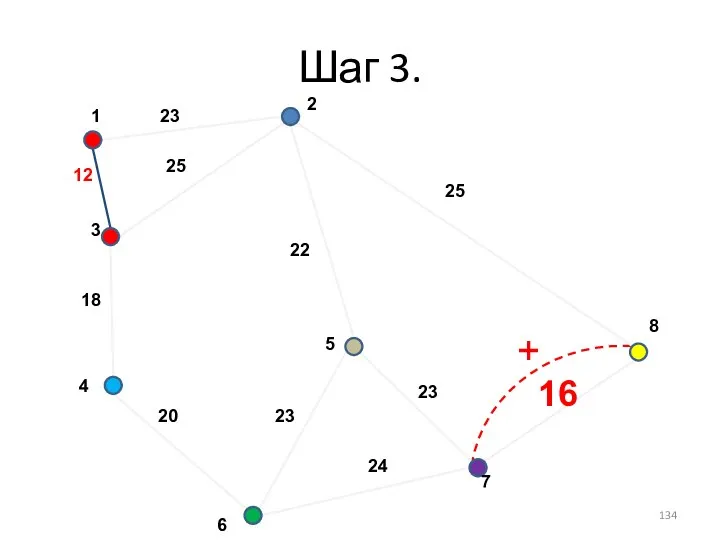
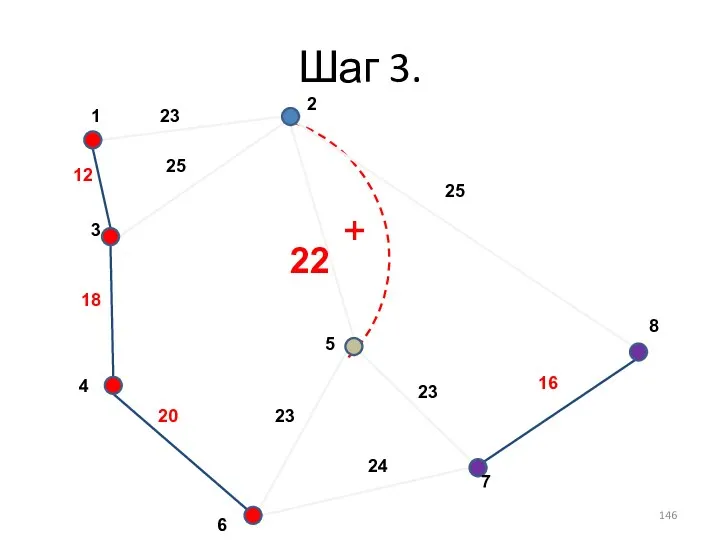
- 134. Шаг 3. +
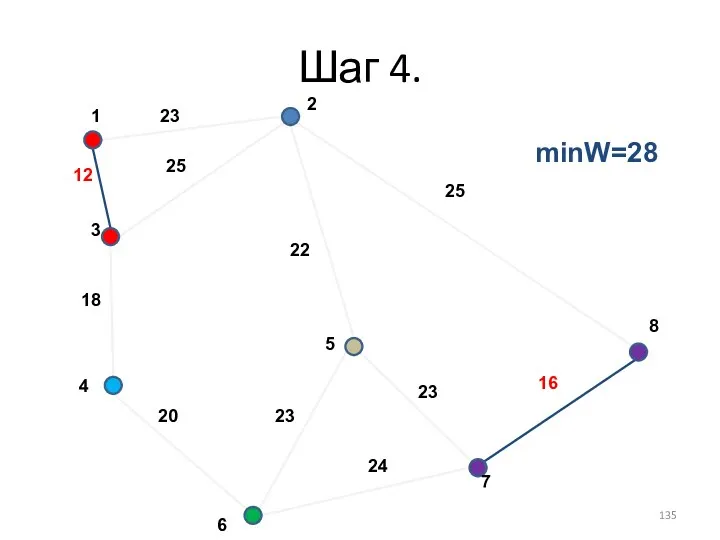
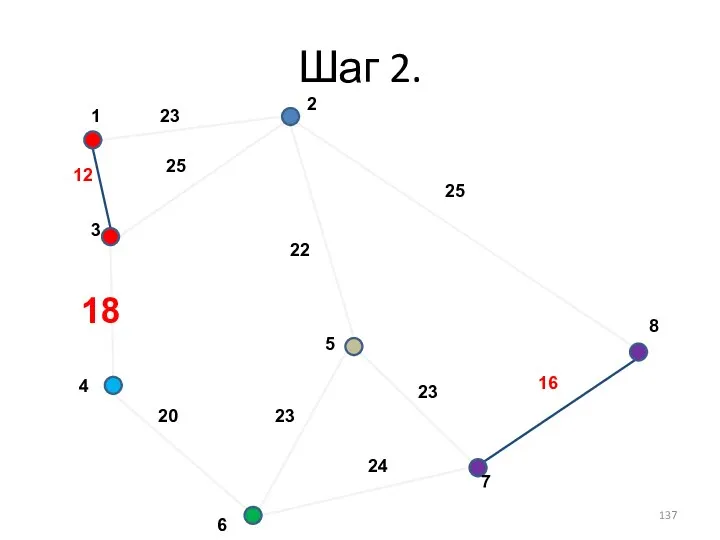
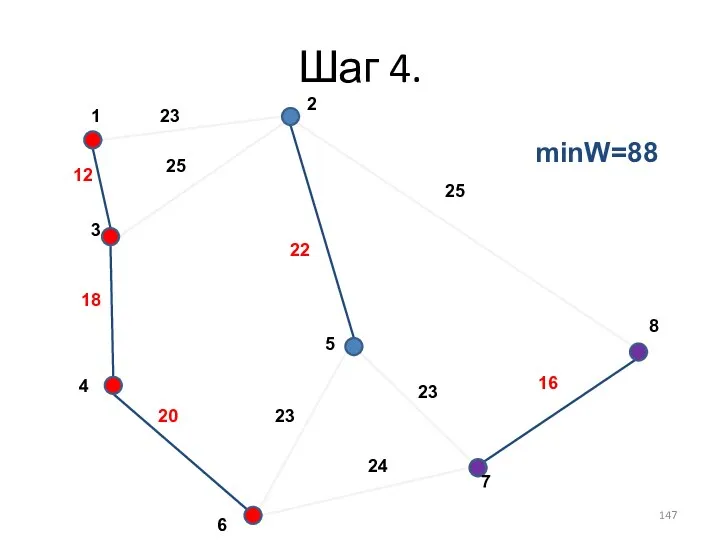
- 135. Шаг 4. minW=28
- 136. Шаг 2. - -
- 137. Шаг 2.
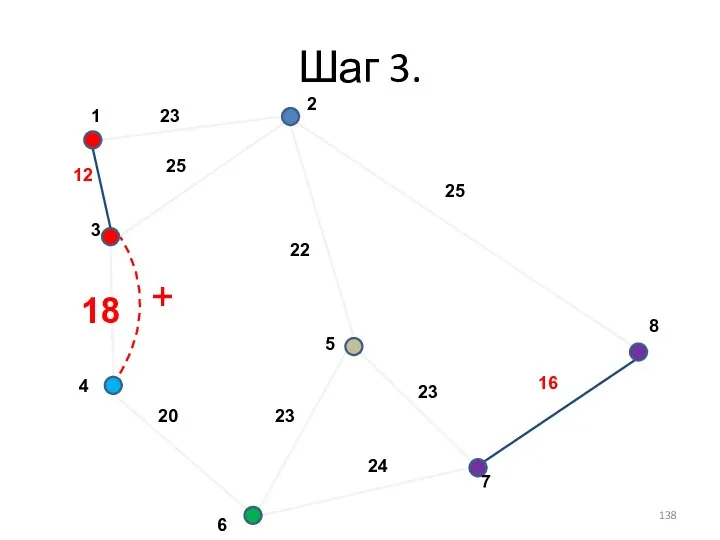
- 138. Шаг 3. +
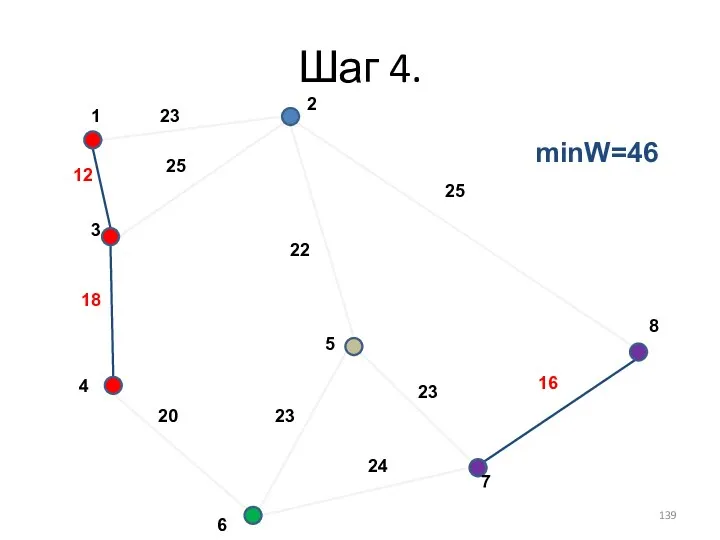
- 139. Шаг 4. minW=46
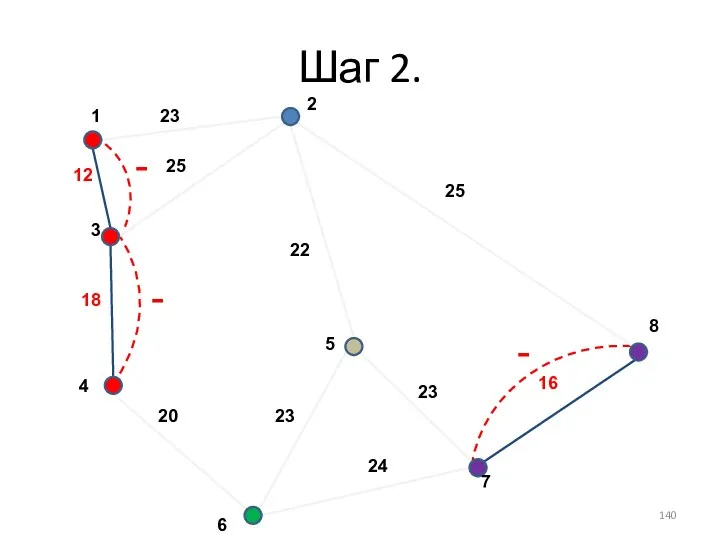
- 140. Шаг 2. - - -
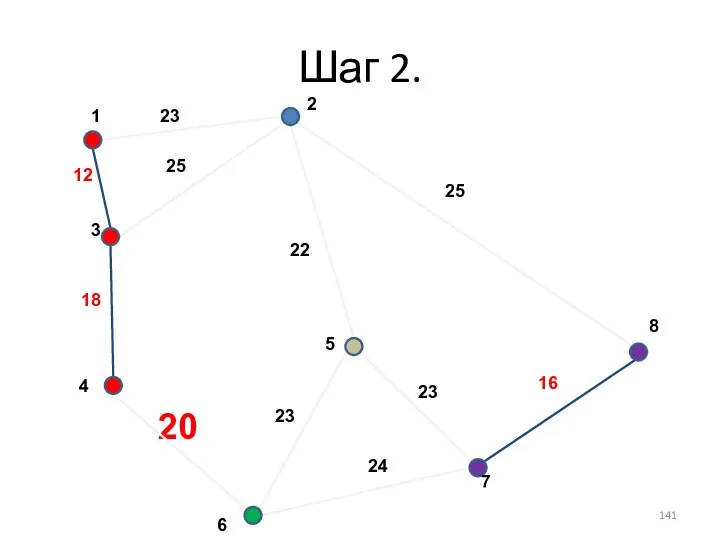
- 141. Шаг 2.
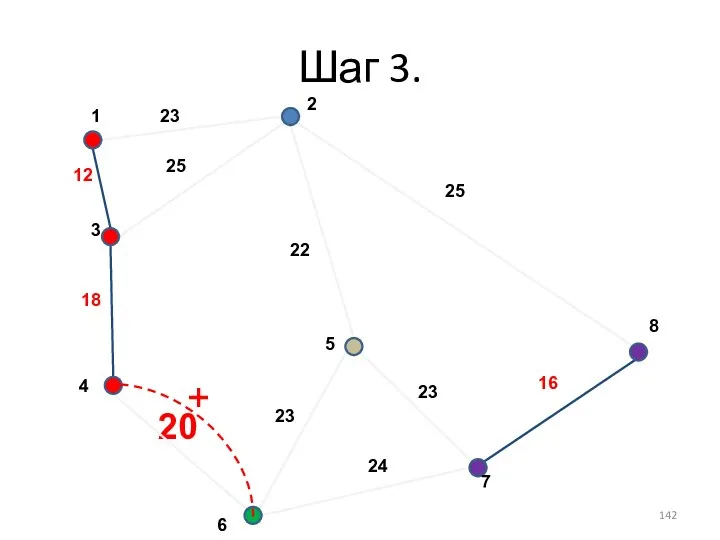
- 142. Шаг 3. +
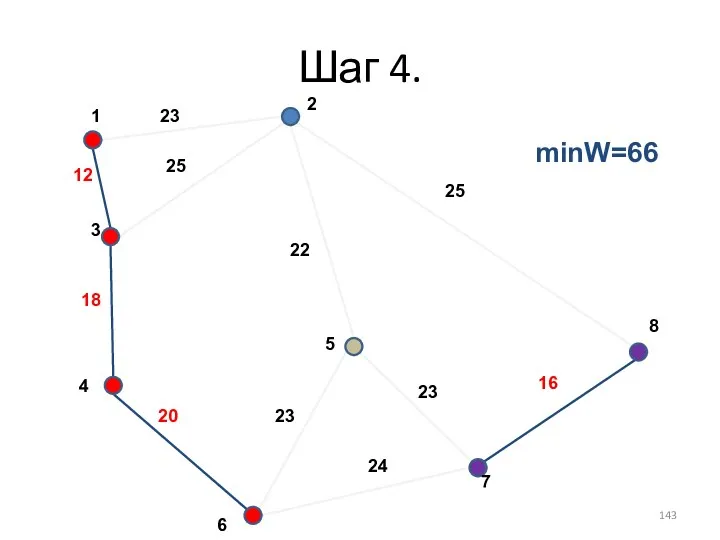
- 143. Шаг 4. minW=66
- 144. Шаг 2. - - - -
- 145. Шаг 2.
- 146. Шаг 3. +
- 147. Шаг 4. minW=88
- 148. Шаг 2. - - - - -
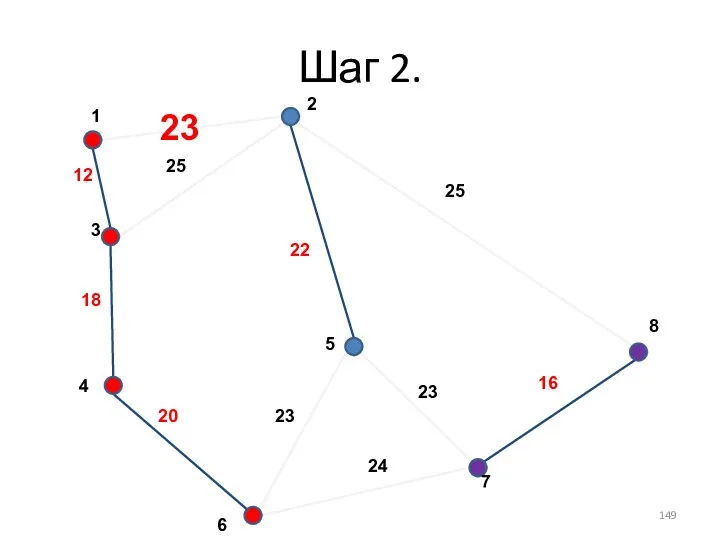
- 149. Шаг 2.
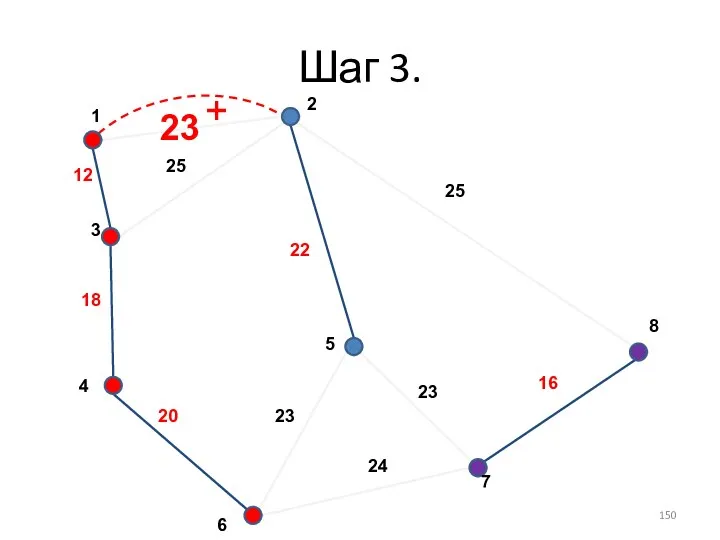
- 150. Шаг 3. +
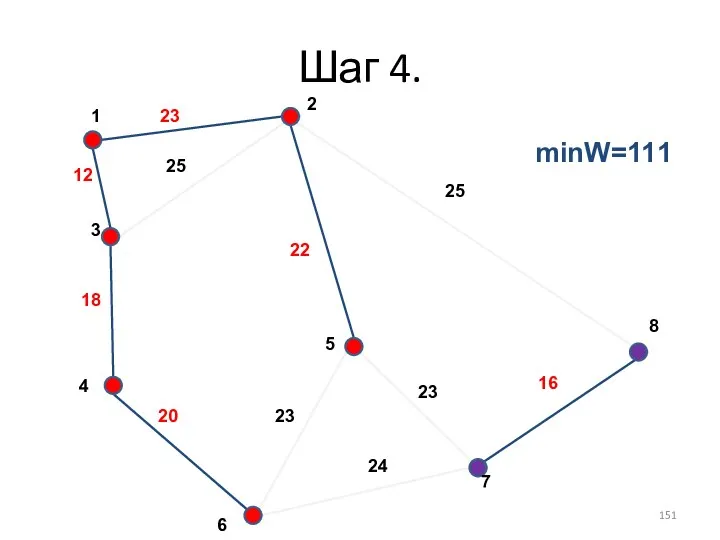
- 151. Шаг 4. minW=111
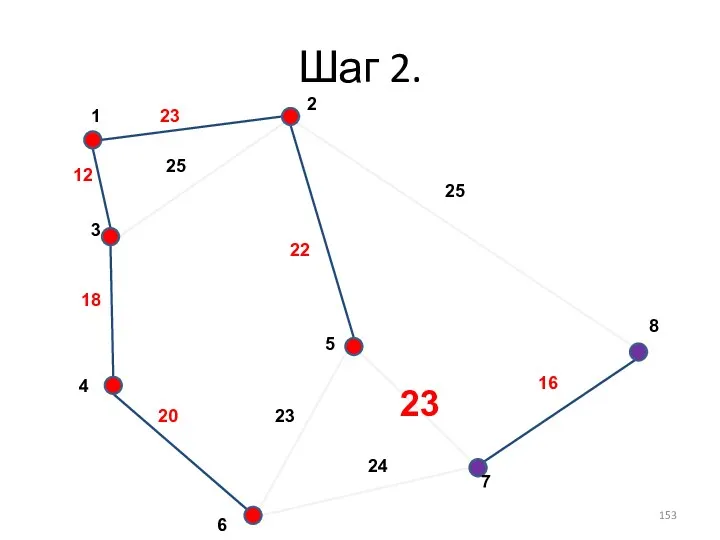
- 152. Шаг 2. - - - - - - -
- 153. Шаг 2.
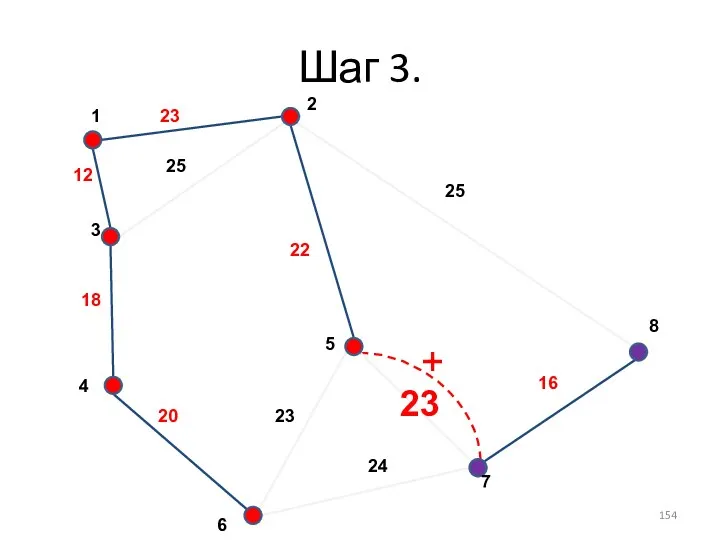
- 154. Шаг 3. +
- 155. Шаг 4. minW=134
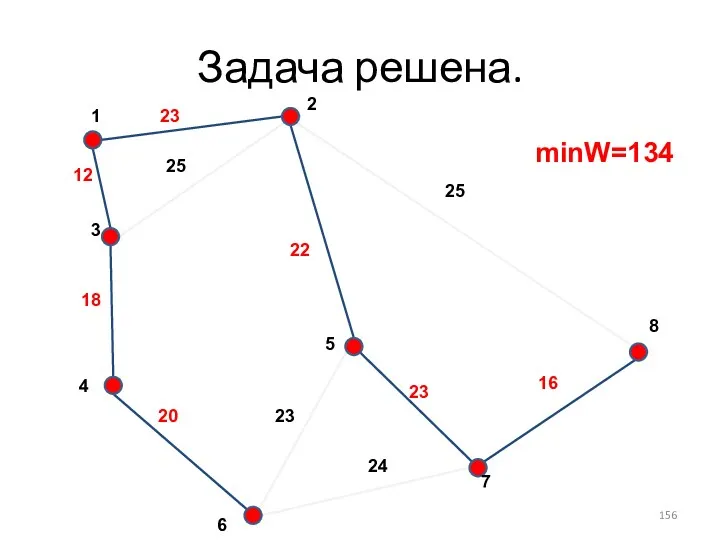
- 156. Задача решена. minW=134
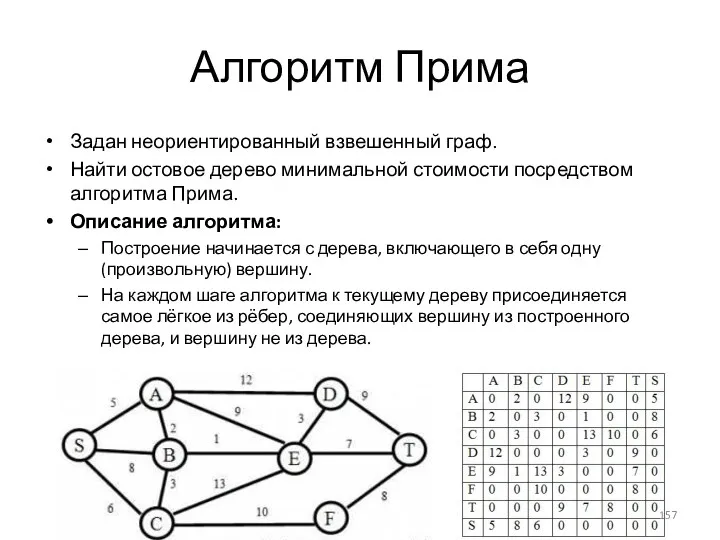
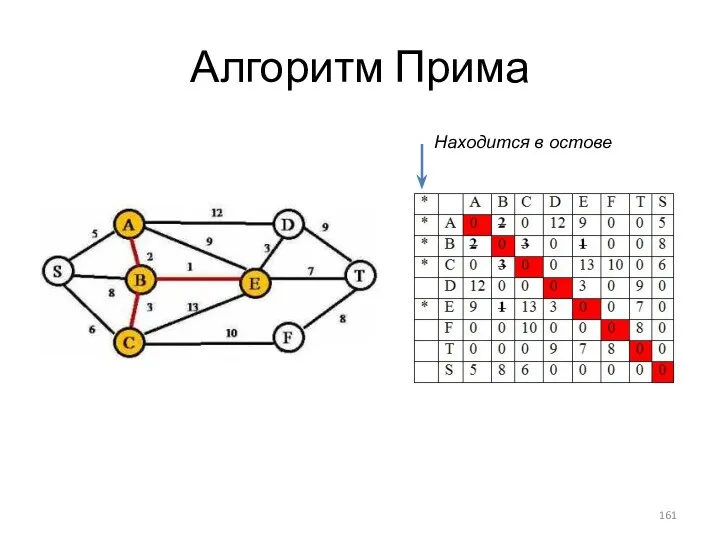
- 157. Алгоритм Прима Задан неориентированный взвешенный граф. Найти остовое дерево минимальной стоимости посредством алгоритма Прима. Описание алгоритма:
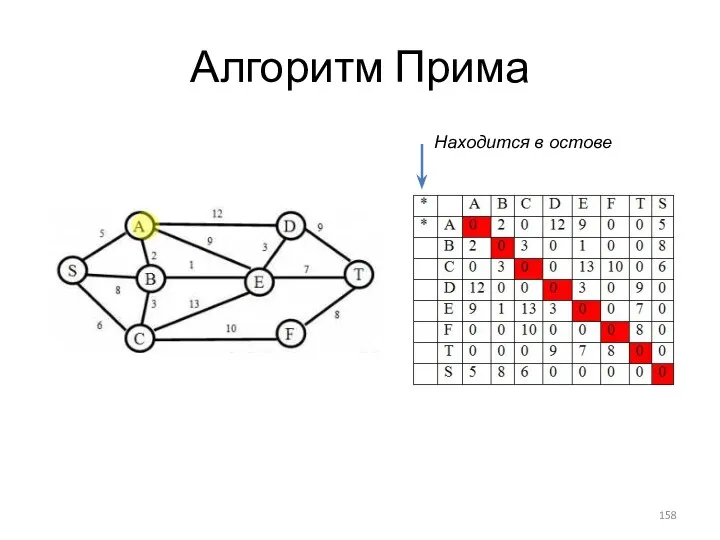
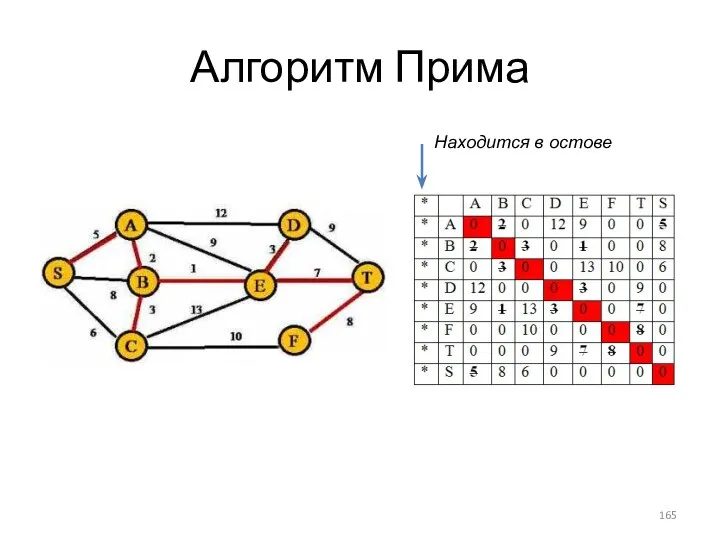
- 158. Алгоритм Прима Находится в остове
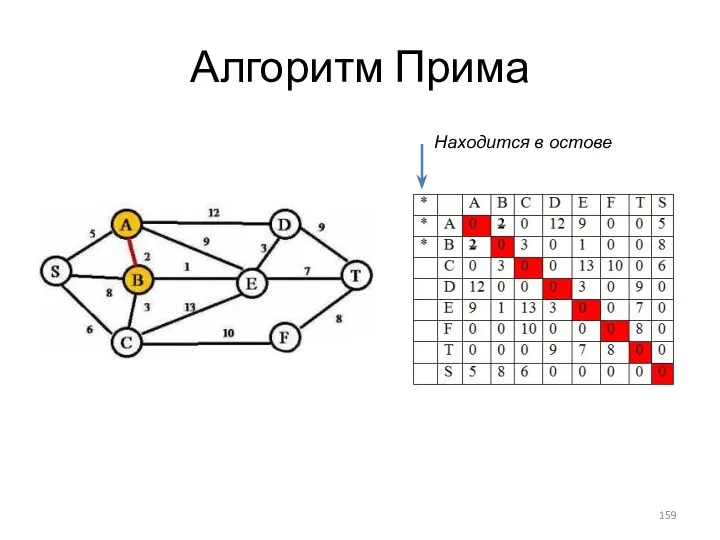
- 159. Алгоритм Прима Находится в остове
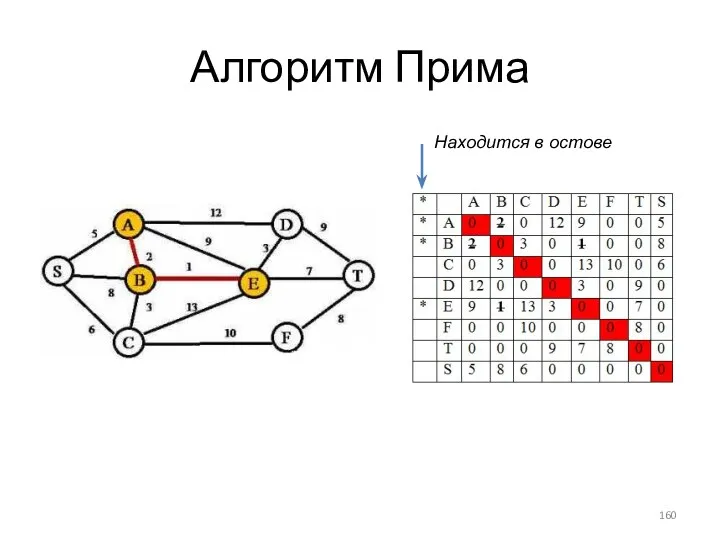
- 160. Алгоритм Прима Находится в остове
- 161. Алгоритм Прима Находится в остове
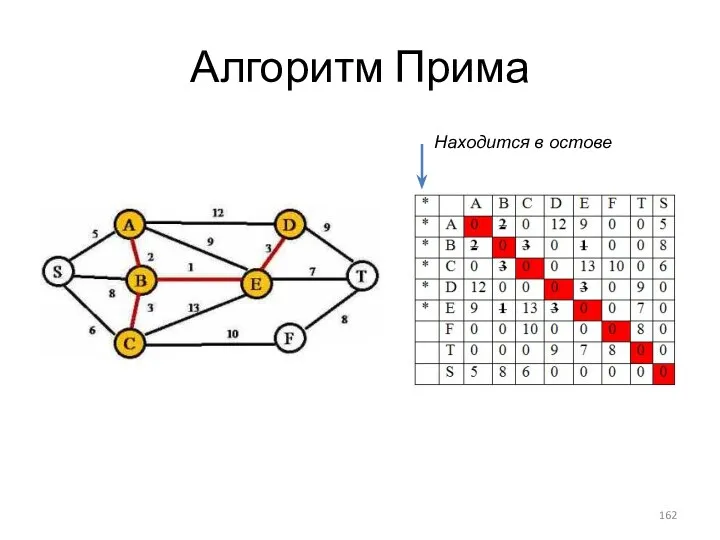
- 162. Алгоритм Прима Находится в остове
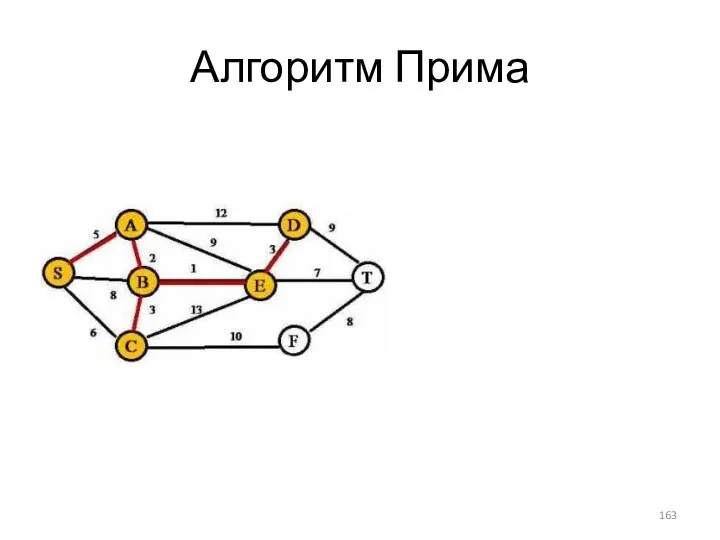
- 163. Алгоритм Прима
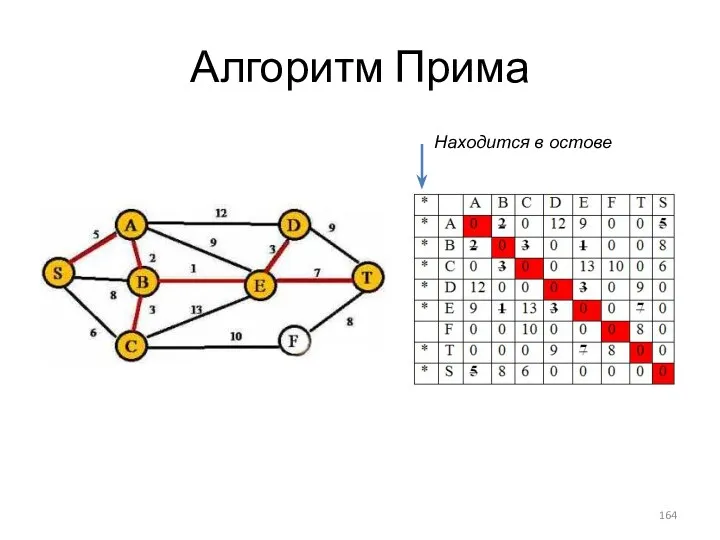
- 164. Алгоритм Прима Находится в остове
- 165. Алгоритм Прима Находится в остове
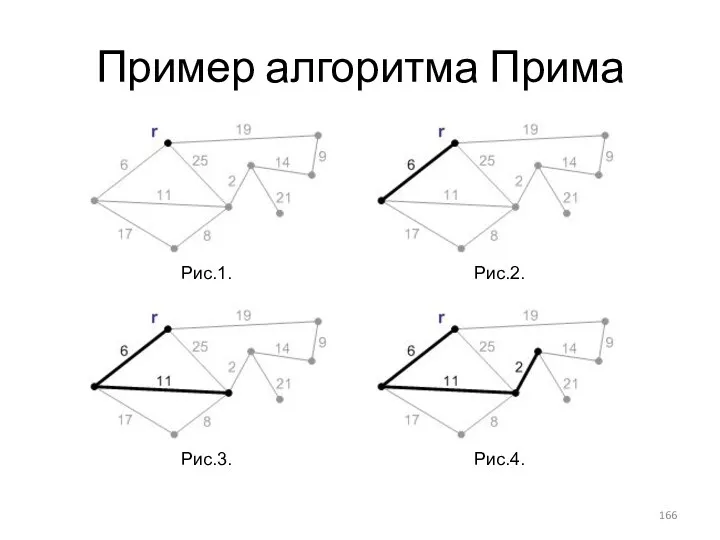
- 166. Пример алгоритма Прима Рис.1. Рис.2. Рис.3. Рис.4.
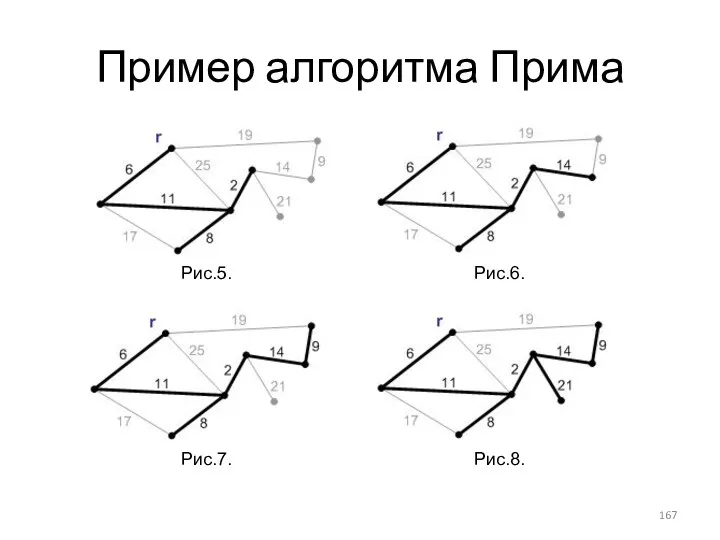
- 167. Пример алгоритма Прима Рис.5. Рис.6. Рис.7. Рис.8.
- 169. Скачать презентацию







































 Инструкция по работе с мобильным приложением E-Salyq Azamat в части подачи ФНО 250.00
Инструкция по работе с мобильным приложением E-Salyq Azamat в части подачи ФНО 250.00 Конкурс Мой безопасный Интернет, Интернет: вред и польза
Конкурс Мой безопасный Интернет, Интернет: вред и польза HTML-VR: программируемые 3D кнопки-гиперссылки и 3Dpx объекты
HTML-VR: программируемые 3D кнопки-гиперссылки и 3Dpx объекты Программирование на языке Python. § 62. Массивы
Программирование на языке Python. § 62. Массивы Методы ООП. Введение в шаблоны. Тема 17
Методы ООП. Введение в шаблоны. Тема 17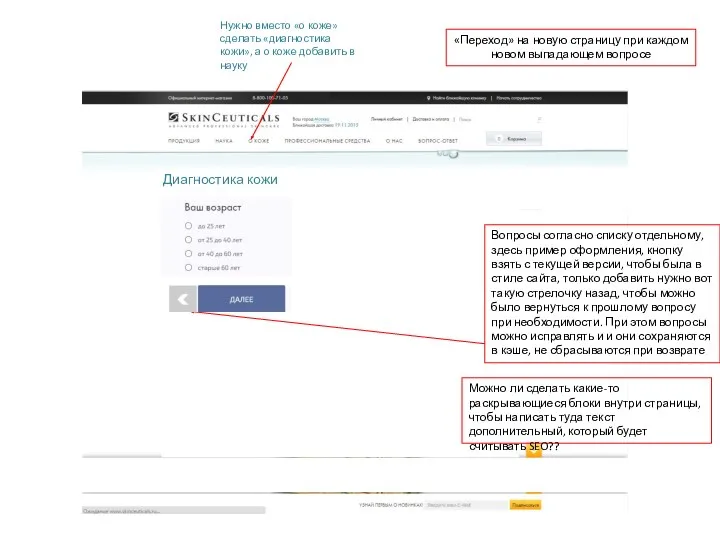 Оформление сайта. Диагностика кожи
Оформление сайта. Диагностика кожи Основи програмної інженерії (лекція 1)
Основи програмної інженерії (лекція 1) Сети и сетевое оборудование
Сети и сетевое оборудование Алгоритм Forel. Выделение устойчивых таксонов
Алгоритм Forel. Выделение устойчивых таксонов Принципи побудови комутаторів та комутаційних середовищ паралельних КС. (Тема 15)
Принципи побудови комутаторів та комутаційних середовищ паралельних КС. (Тема 15) Управление памятью. Функции ОC по управлению памятью
Управление памятью. Функции ОC по управлению памятью Устройство компьютера (10 класс)
Устройство компьютера (10 класс) Представление чисел в компьютере. Математические основы информатики
Представление чисел в компьютере. Математические основы информатики Отображение информации с помощью аудио и видео средств вычислительной техники
Отображение информации с помощью аудио и видео средств вычислительной техники Передача информации. Схема передачи информации. Электронная почта
Передача информации. Схема передачи информации. Электронная почта Работа с интерактивной доской StarBoard
Работа с интерактивной доской StarBoard Новые онлайн кассы в 2017 году. Изменения в законе № 54 ФЗ
Новые онлайн кассы в 2017 году. Изменения в законе № 54 ФЗ Буква - строка - текст. Искусство шрифта
Буква - строка - текст. Искусство шрифта Компьютерна я безопасность
Компьютерна я безопасность Выполнения алгоритма
Выполнения алгоритма Азы программирования на языке LabView. Первая модель робота LegoWeDo
Азы программирования на языке LabView. Первая модель робота LegoWeDo Уровни представления данных. Функции СУБД. (Лекция 2)
Уровни представления данных. Функции СУБД. (Лекция 2) Настройка интеграции базы 1С с внешними системами. Типичные ситуации
Настройка интеграции базы 1С с внешними системами. Типичные ситуации Database Management System
Database Management System Устройства ввода и вывода информации
Устройства ввода и вывода информации Жесткий диск
Жесткий диск 1С: Лекторий
1С: Лекторий Алгоритм із повторенням
Алгоритм із повторенням