Содержание
- 2. Introduction /63
- 3. THIS IS NOT A LECTURE /63
- 4. Lets inquire and discover together! /63
- 5. What is programming? /63
- 6. OOP point of view Class diagram /63
- 7. OOP point of view Sequence diagram /63
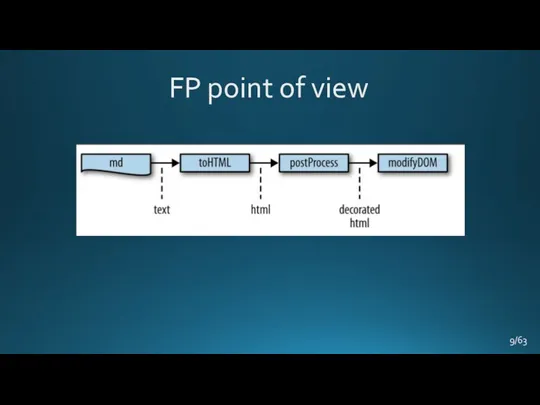
- 8. FP point of view /63
- 9. FP point of view /63
- 10. What is similar between those POVs? /63
- 11. Composition /63
- 12. Programming is Composition /63
- 13. Is there any science which is focused on composition? /63
- 14. Yes, it is Category Theory /63
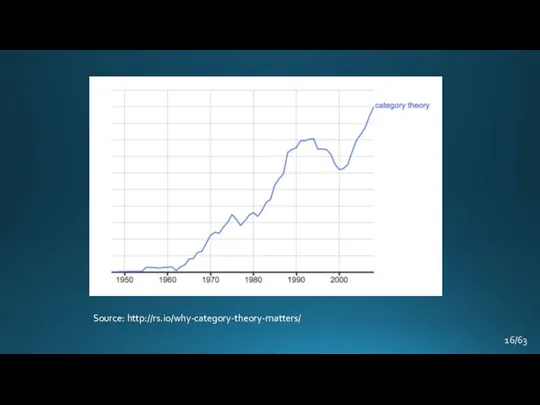
- 15. Why to study CT? /63
- 16. Source: http://rs.io/why-category-theory-matters/ /63
- 17. Why to study CT? Extremely general and wide-applicable Gives the new way (not set-theoretic) to look
- 18. Why to study CT? programming /63
- 19. Why to study CT for software engineer? Growing complexity of software systems and multicore\distributed systems revolution
- 20. What is a Category? /63
- 21. /63
- 22. Category is: Objects Arrows between objects Composition rule: ( . ) :: (a → b) →
- 23. Associativity of composition What? /63
- 24. Associativity of composition What? /63
- 25. Order of the operations doesn’t matter Associativity of composition Why? /63
- 26. Identity Arrow What? /63
- 27. Identity Arrow What? /63
- 28. Identity Arrow What? /63
- 29. It is neutral element (‘zero’) for the composition (id x = х). It gives us a
- 30. Examples /63
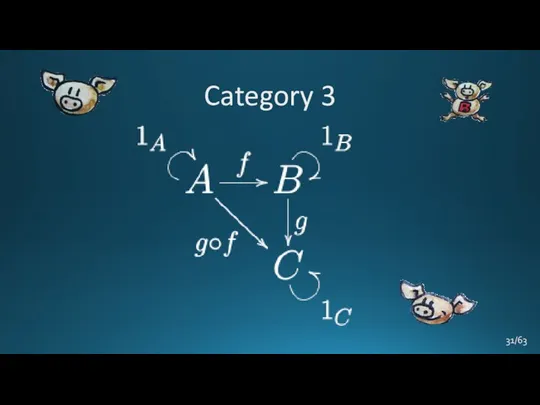
- 31. Category 3 /63
- 32. Category 1 /63
- 33. Category 0 /63
- 34. Integer Category Objects: singleton (set with only one element in it) Arrows: all possible integers Composition:
- 35. String Category Objects: singleton Arrows: all possible strings Composition: ++ - string concatenation Identity: «» -
- 36. Monoids Set-theoretic approach Set M Binary operation •: M × M → M For all a,
- 37. Examples: Monoids Category-theoretic approach /63
- 38. Monoids Category-theoretic approach /63
- 39. Set Category Objects: all sets. Arrows: functions between sets. Identity: id function between sets. Composition: (
- 40. Hask Category Objects: types in Haskell Arrows: functions between them (everything is pure!) Identity: id function:
- 41. /63
- 42. Functions /63
- 43. Functions in categories: Functors /63
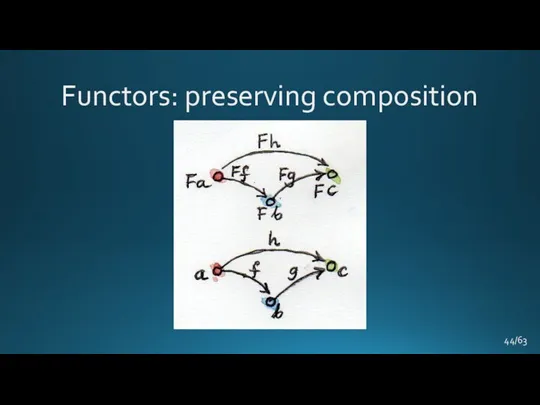
- 44. Functors: preserving composition /63
- 45. Functors: preserving identities /63
- 46. Functors: in brief Maps objects to objects Maps arrows to arrows Preserve composition and identities /63
- 47. Example /63
- 48. /63
- 49. Why is that useful? /63
- 50. /63
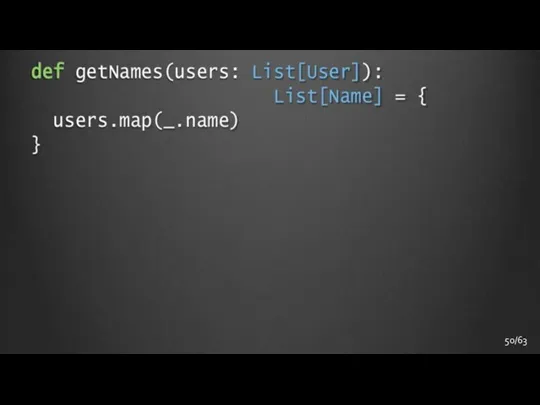
- 51. 41/50 51/63
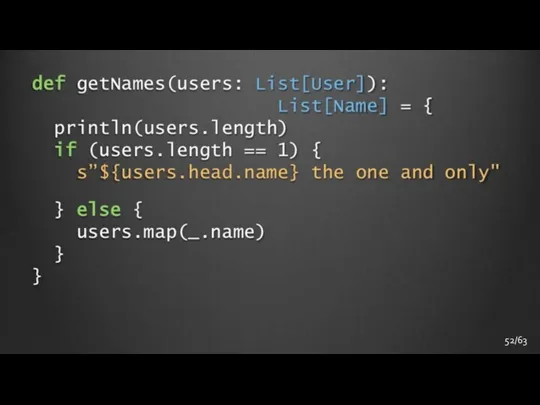
- 52. 52/63
- 53. Wait, but what if you’ll need one more container type ? 53/63
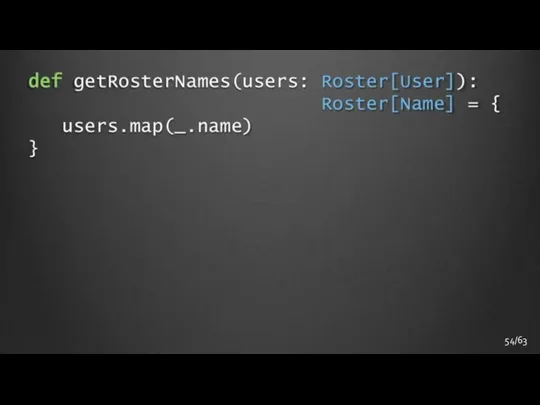
- 54. 54/63
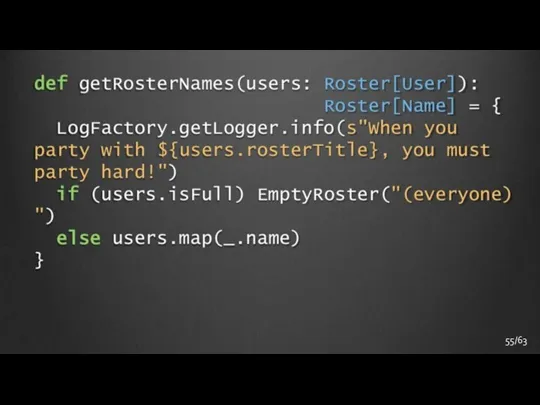
- 55. 55/63
- 56. How to rescue the situation? 56/63
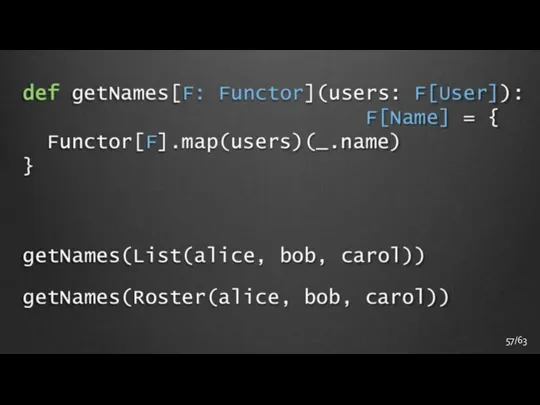
- 57. 57/63
- 58. Conclusions and some further thoughts CT and programming are tightly connected through composition CT – source
- 59. Acknowledgements /63
- 60. Acknowledgements /63
- 61. Acknowledgements Richard Feynman Jiddu Krishnamurti /63
- 62. Q&A /63
- 64. Скачать презентацию




















































 Создание лексико-семантической основы ИПЯ
Создание лексико-семантической основы ИПЯ Базы данных
Базы данных Эталонная модель сетевого взаимодействия OSI
Эталонная модель сетевого взаимодействия OSI Белгі бойынша көпхаттамалы коммутация технологиясының жұмысын өңдеу
Белгі бойынша көпхаттамалы коммутация технологиясының жұмысын өңдеу Тестировщик программного обеспечения. Итоговый проект Сайт Beerkontora.ru
Тестировщик программного обеспечения. Итоговый проект Сайт Beerkontora.ru Обработка текстовой и графической информации
Обработка текстовой и графической информации Сетевые операционные системы
Сетевые операционные системы Комп’ютерні віруси
Комп’ютерні віруси Пошук матеріалів в Інтернеті та їх оцінювання
Пошук матеріалів в Інтернеті та їх оцінювання Инфраструктура открытых ключей
Инфраструктура открытых ключей Database Systems Development. Lecture. 1 Introduction to Database Systems
Database Systems Development. Lecture. 1 Introduction to Database Systems Hashtag my day. User story
Hashtag my day. User story Надійність, діагностика та експлуатація комп’ютерних систем та мереж
Надійність, діагностика та експлуатація комп’ютерних систем та мереж Разработка утилиты для обфускации веб-приложений
Разработка утилиты для обфускации веб-приложений Технология Drag and Drop
Технология Drag and Drop Онлайн – ресурсы для поиска работы и найма персонала
Онлайн – ресурсы для поиска работы и найма персонала Строки. Регулярные выражения
Строки. Регулярные выражения Интернет. Глобальная компьютерная сеть
Интернет. Глобальная компьютерная сеть Базы данных. Основные понятия
Базы данных. Основные понятия Операционные системы. Файловые системы. Загрузчики. Виртуальные среды
Операционные системы. Файловые системы. Загрузчики. Виртуальные среды Расширить поле до 1170px
Расширить поле до 1170px Моделирование памяти. Информационные объекты MATRIX. Организация циклов
Моделирование памяти. Информационные объекты MATRIX. Организация циклов Інформаційні характеристики каналів зв'язку
Інформаційні характеристики каналів зв'язку Поняття про базу даних як основну складову будь-якої ІС
Поняття про базу даних як основну складову будь-якої ІС Понятие ресурса ОС
Понятие ресурса ОС Обработка форм
Обработка форм ПОРТФОЛИО ДОСТИЖЕНИЙ
ПОРТФОЛИО ДОСТИЖЕНИЙ Потоки и процессы
Потоки и процессы