Содержание
- 2. Определение (рекурсивное) 1. Одиночная вершина есть двоичное дерево. 2. Двоичное дерево – это вершина (V), соединенная
- 3. Пример двоичного дерева Кружочками обозначены вершины дерева, стрелками - связи между вершинами.
- 4. Высота дерева (h) определяется как число вершин в самой длинной ветви дерева. Начальная вершина называется корнем.
- 5. Словарь tree [три] – дерево root [рут] – корень vertex [вётэкс] – вершина right [райт] –
- 6. Свойство 1: Максимальное число вершин в двоичном дереве высоты h равно nmax(h)= 2h – 1 Доказательство:
- 7. Свойство 2: Минимально возможная высота двоичного дерева с n вершинами равна hmin(n) = ⎡log(n+1)⎤ Доказательство: Из
- 8. Определение Двоичное дерево называют идеально сбалансированным (ИСД), если для каждой его вершины размеры левого и правого
- 9. Пример
- 10. Свойство 3: Высота ИСД с n вершинами минимальна. hисд(n) = hmin(n) = ⎡log(n+1)⎤
- 11. Каждая вершина содержит данные и указатели на вершину слева и справа. В качестве заголовка для дерева
- 12. Структура вершины дерева struct Vertex { int Data; Vertex * Left; Vertex * Right; } ;
- 13. Графическое представление
- 14. Существует много работ, которые можно выполнять с деревьями. Например, посадка, подкормка, подстрижка, полив, окучивание и т.п.
- 15. Основные операции с деревьями Определение. Обход дерева – выполнение некоторой операции с каждой его вершиной. Существуют
- 16. Обходы легко программируются с помощью рекурсивных процедур. Пример. Процедура обхода дерева сверху вниз. void Obhod1 (
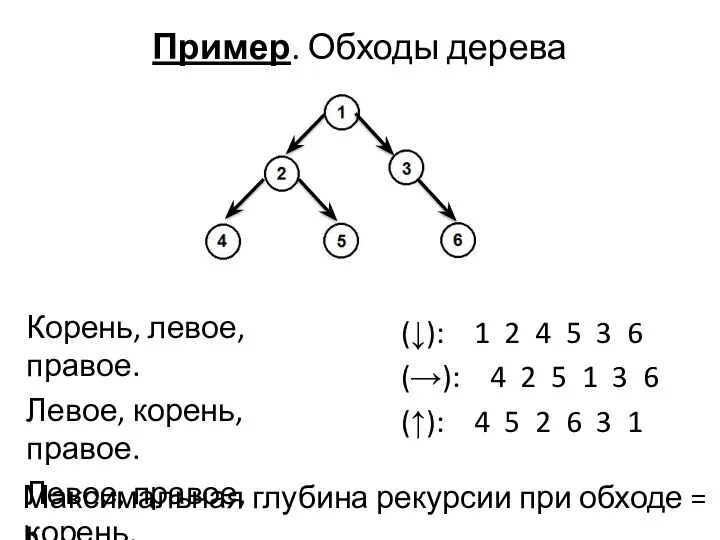
- 17. Пример. Обходы дерева Корень, левое, правое. Левое, корень, правое. Левое, правое, корень. (↓): 1 2 4
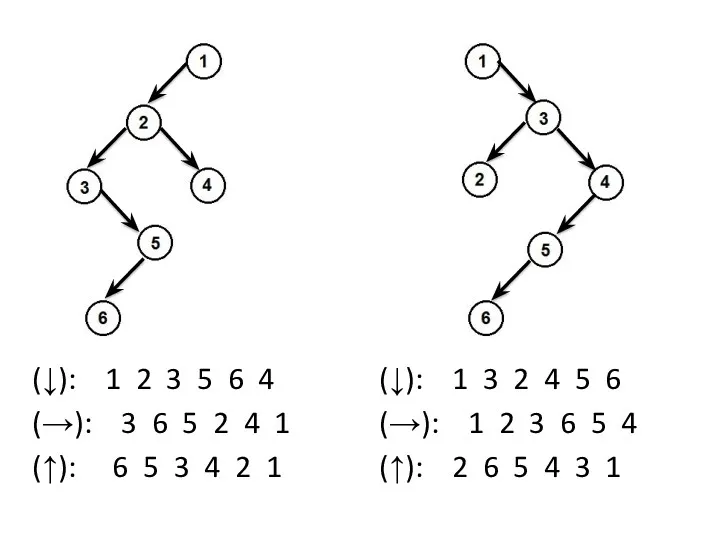
- 18. (↓): 1 3 2 4 5 6 (→): 1 2 3 6 5 4 (↑): 2
- 19. 3.9. Деревья поиска Двоичные деревья часто используются для представления данных, среди которых идет поиск элементов по
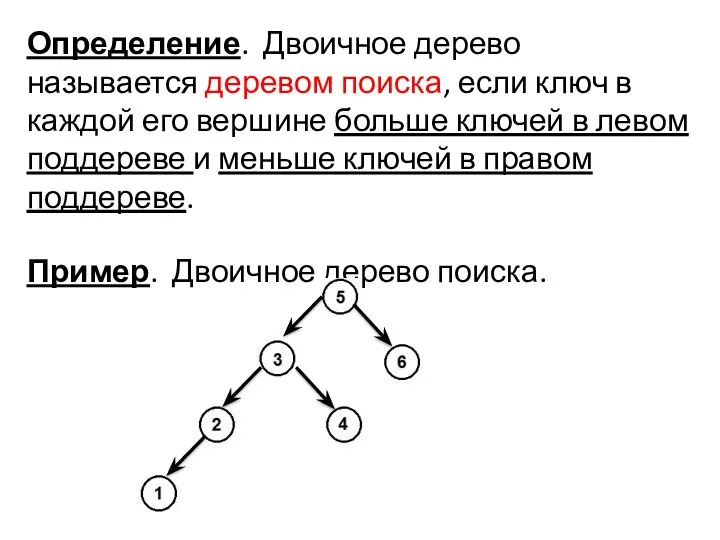
- 20. Определение. Двоичное дерево называется деревом поиска, если ключ в каждой его вершине больше ключей в левом
- 21. 3.9.1. Поиск вершины с ключом Х Начиная с корневой вершины дерева, сравниваем ключ поиска с данными
- 22. Поиск вершины с ключом Х Алгоритм на псевдокоде p := Root DO (p != NULL) IF
- 23. Трудоемкость поиска по дереву Максимальное количество сравнений при поиске: Cmax =2h Идеально сбалансированное дерево: Cmax= 2
- 24. Построение ИСДП из элементов массива А = (a1, a2 ,…, an): Отсортировать массив по возрастанию. Построить
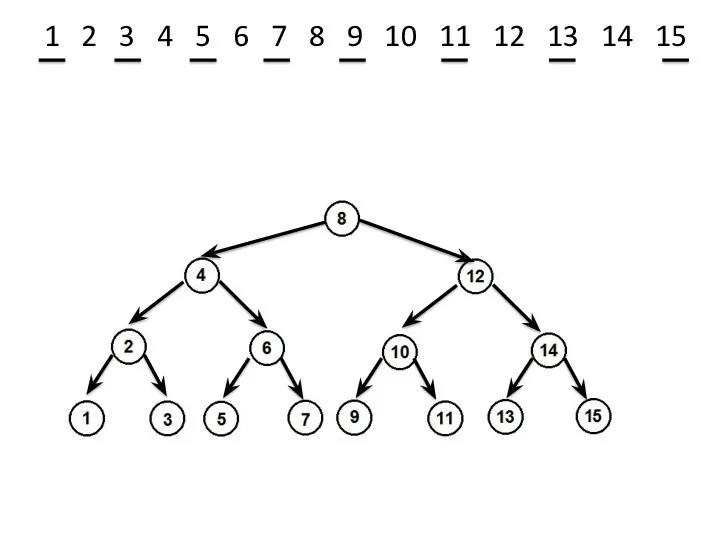
- 25. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
- 26. Построение ИСДП Алгоритм на псевдокоде Vertex* ISDP (L,R) IF (L>R) return NULL; ELSE m := ⎡(L+R)/2⎤
- 27. В реальности количество элементов данных заранее неизвестно и они поступают последовательно в произвольном порядке. Требуется строить
- 28. Случайные деревья поиска. Все преимущества деревьев реализуются именно тогда, когда меняется их структура в ходе выполнения
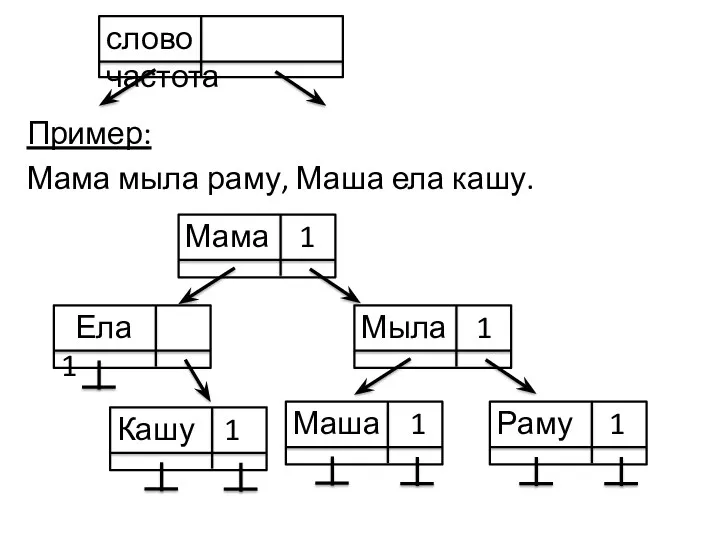
- 29. Пример: Мама мыла раму, Маша ела кашу. слово частота Мама 1 Ела 1 Мыла 1 Раму
- 30. Построение СДП Идея: построение выполняется путем добавления новых вершин в дерево. Если дерево пустое, то создать
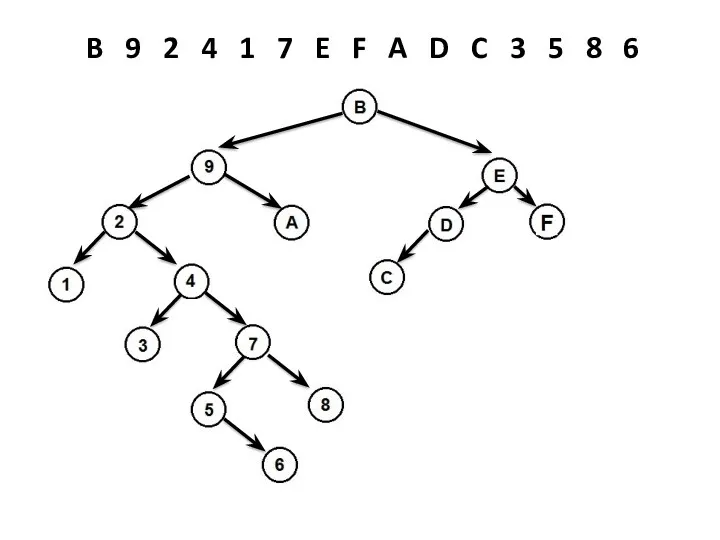
- 31. B 9 2 4 1 7 E F A D C 3 5 8 6
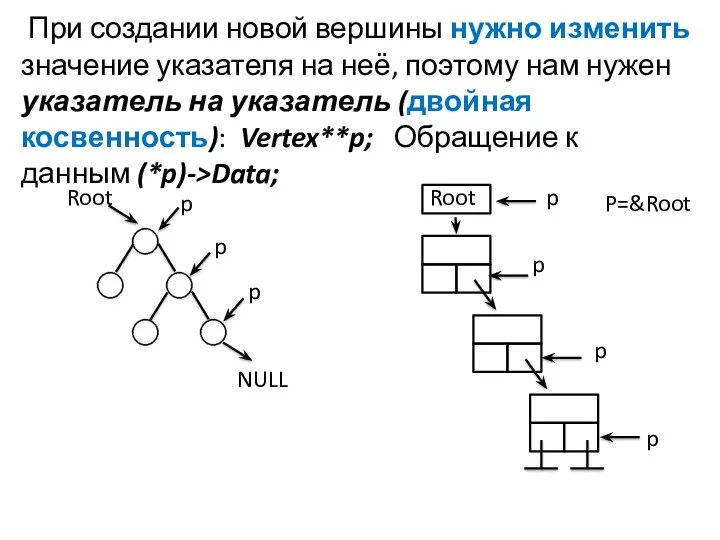
- 32. При создании новой вершины нужно изменить значение указателя на неё, поэтому нам нужен указатель на указатель
- 33. Обозначения: Root - корень, D – данные, p - указатель на указатель Добавить (данные D в
- 34. Хотя назначение этого алгоритма - поиск с включением, его можно использовать и для сортировки. Если мы
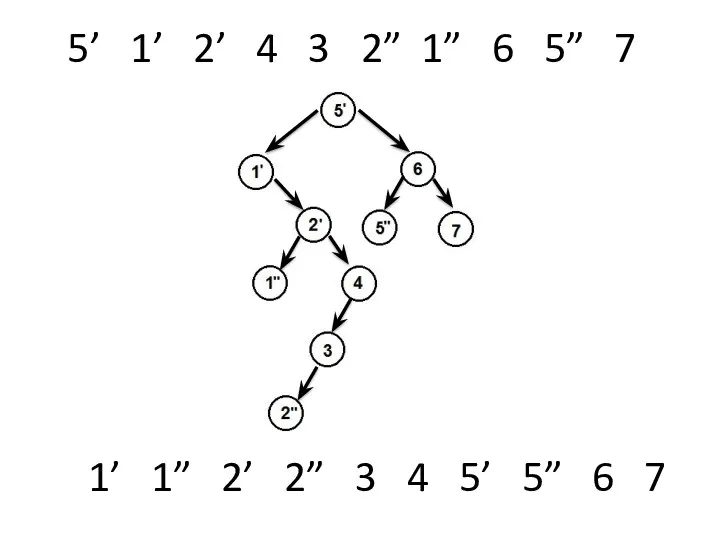
- 35. 5’ 1’ 2’ 4 3 2” 1” 6 5” 7 1’ 1” 2’ 2” 3 4
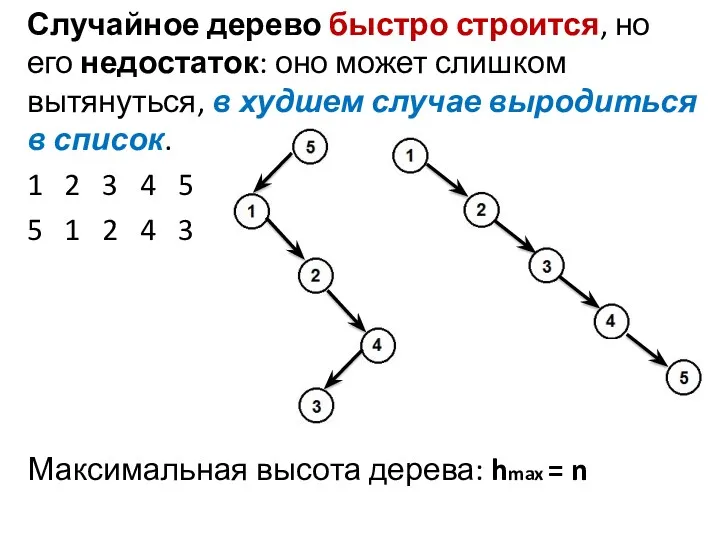
- 36. Случайное дерево быстро строится, но его недостаток: оно может слишком вытянуться, в худшем случае выродиться в
- 39. Скачать презентацию



![Словарь tree [три] – дерево root [рут] – корень vertex](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/588464/slide-4.jpg)























 Интеллектуальные информационные системы (ИИС). Лекция 7. Нечеткий логический вывод
Интеллектуальные информационные системы (ИИС). Лекция 7. Нечеткий логический вывод Информационная деятельность человека: сбор, обработка, хранение, передача, защита информации. Урок №2
Информационная деятельность человека: сбор, обработка, хранение, передача, защита информации. Урок №2 Все на поиск терминов. Компьютерный турнир
Все на поиск терминов. Компьютерный турнир Системы управления базами данных (СУБД) MS Access
Системы управления базами данных (СУБД) MS Access Мультимедийная презентация-сказкаРепкав технике оригами.
Мультимедийная презентация-сказкаРепкав технике оригами. Основные сведения о персональных компьютерах. (Тема 4)
Основные сведения о персональных компьютерах. (Тема 4) Устройство компьютера
Устройство компьютера Apache Kafka
Apache Kafka Настройка сетевых параметров операционных систем Windows и Linux
Настройка сетевых параметров операционных систем Windows и Linux Типы информационных моделей. Основные этапы разработки и исследования моделей на компьютере
Типы информационных моделей. Основные этапы разработки и исследования моделей на компьютере Цветовые модели компьютерной графики
Цветовые модели компьютерной графики Разработка движка для сайта “Музыкальный портал”
Разработка движка для сайта “Музыкальный портал” Диаграмма состояний. Применение языка UML при разработке информационных систем
Диаграмма состояний. Применение языка UML при разработке информационных систем Графика в Pascal ABC
Графика в Pascal ABC Система Ладошки
Система Ладошки Электронное правительство
Электронное правительство Технологии обработки данных. Сетевые технологии обработки данных. (Лекция 8)
Технологии обработки данных. Сетевые технологии обработки данных. (Лекция 8) Модуль 1: Установка и настройка SQL Server 2008
Модуль 1: Установка и настройка SQL Server 2008 Введение в C#. Новый язык от Microsoft
Введение в C#. Новый язык от Microsoft Информация и информационные технологии
Информация и информационные технологии Постановка задачи обеспечения информационной безопасности баз данных
Постановка задачи обеспечения информационной безопасности баз данных Системы управления контентом CMS (08)
Системы управления контентом CMS (08) Spring Framework
Spring Framework Как пройти нормоконтроль
Как пройти нормоконтроль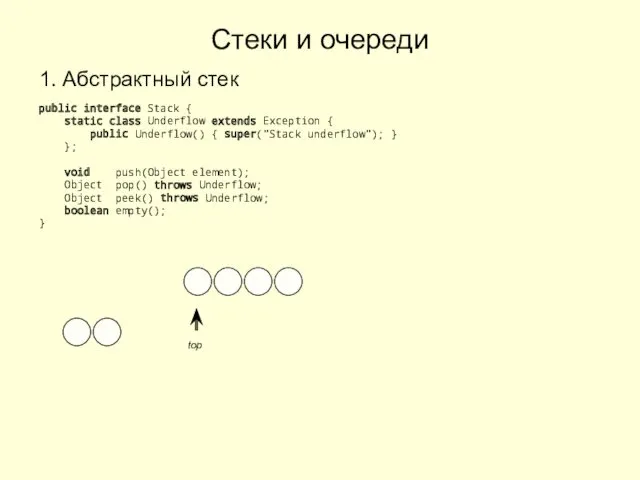 Стеки и очереди
Стеки и очереди Подготовка к ОГЭ (информатика)
Подготовка к ОГЭ (информатика) Аддитивные технологии
Аддитивные технологии Компьютерный сленг и его использование в молодёжной среде
Компьютерный сленг и его использование в молодёжной среде