Содержание
- 2. Оглавление
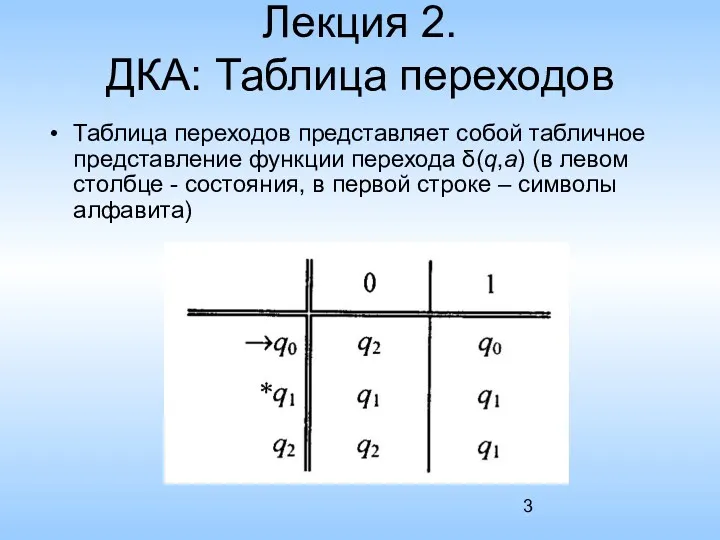
- 3. Лекция 2. ДКА: Таблица переходов Таблица переходов представляет собой табличное представление функции перехода δ(q,a) (в левом
- 4. ДКА: Расширенная функция переходов Расширенная функция переходов ставит в соответствие состоянию q и цепочке w состояние
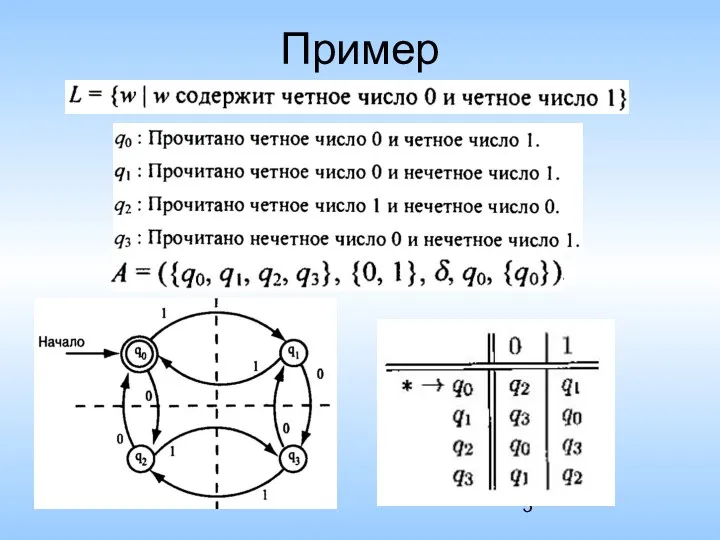
- 5. Пример
- 6. Пример (продолжение) w=110101 Язык ДКА (регулярный язык)
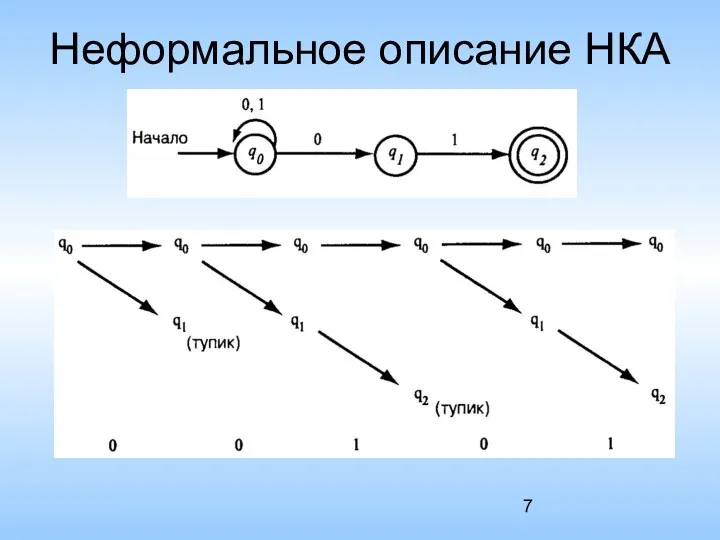
- 7. Неформальное описание НКА
- 8. Формальное определение НКА
- 9. НКА: Расширенная функция переходов Расширенная функция переходов ставит в соответствие состоянию q и цепочке w множество
- 10. Пример w=00101 Язык НКА
- 11. Конструкция подмножеств ДКА обладают всеми возможностями НКА -> L(D)=L( N)
- 12. Конструкция подмножеств (пример) |QD | = QN={q0, q1, q2}
- 13. «Ленивый» алгоритм
- 14. Конструкция подмножеств Базис: |w|=0 -> w=ε -> (по базису определения) = = Индукция: |w| = n+1,
- 15. Теорема
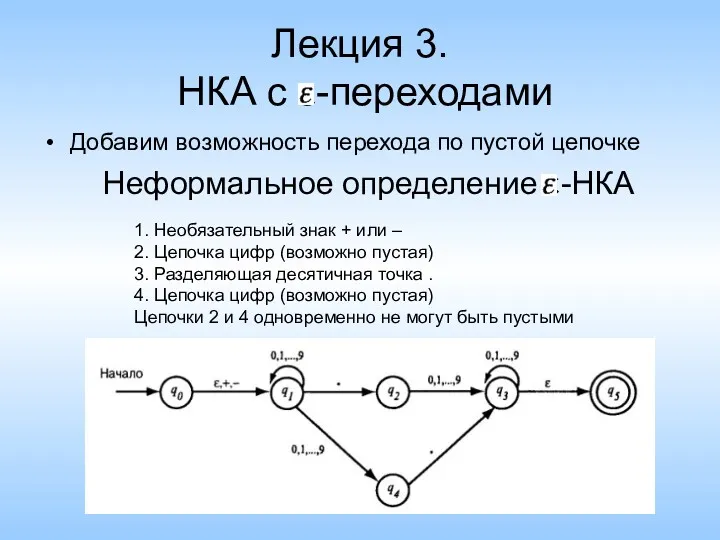
- 16. Лекция 3. НКА с ε-переходами Добавим возможность перехода по пустой цепочке Неформальное определение ε-НКА 1. Необязательный
- 17. Формальное определение ε-НКА
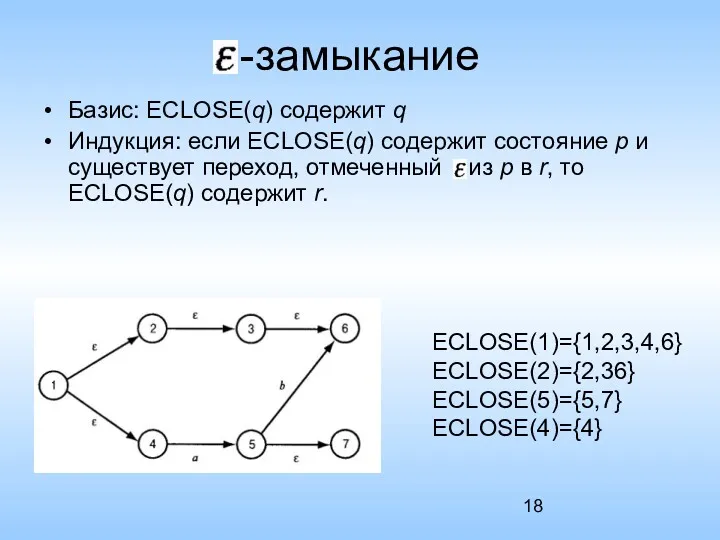
- 18. -замыкание Базис: ECLOSE(q) содержит q Индукция: если ECLOSE(q) содержит состояние p и существует переход, отмеченный из
- 19. -НКА: Расширенная функция переходов Базис: Индукция: пусть w=xa, a из
- 20. Пример
- 21. Устранение -переходов 1. QD есть множество -замкнутых подмножеств QЕ 2. 3. 4.
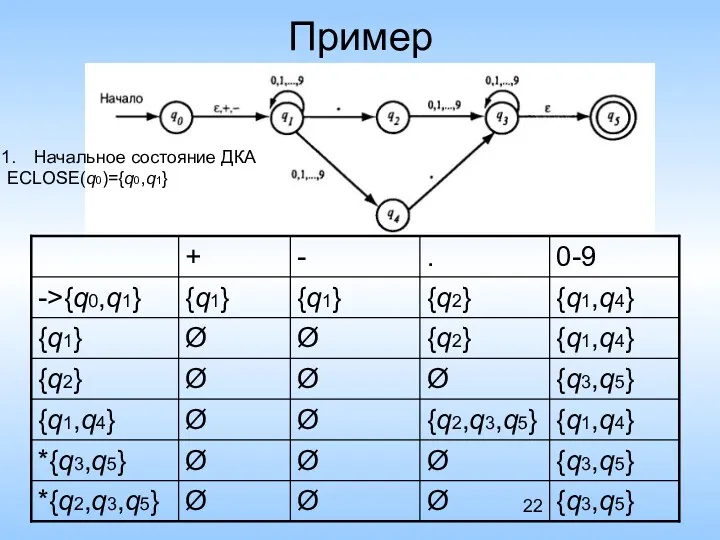
- 22. Пример Начальное состояние ДКА ECLOSE(q0)={q0,q1}
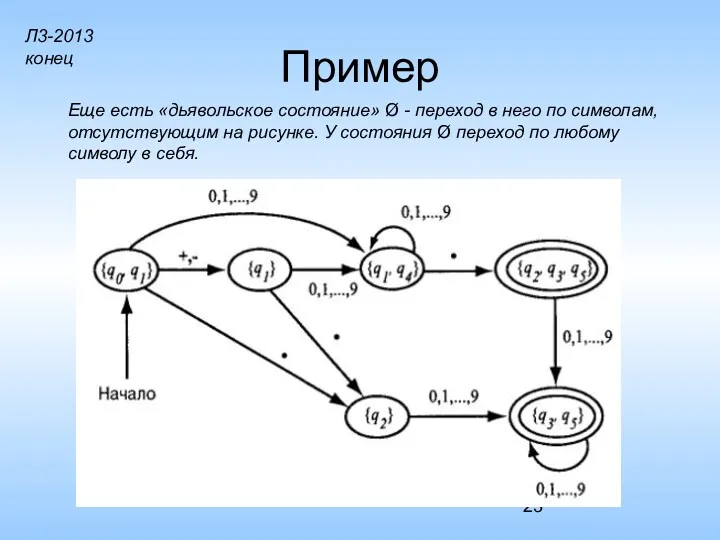
- 23. Пример Еще есть «дьявольское состояние» Ø - переход в него по символам, отсутствующим на рисунке. У
- 24. Теорема Необходимость. Пусть существует ДКА D с языком L=L(D). Преобразуем D в -НКА E. Добавим переходы
- 25. Лекция 4. Регулярные выражения (РВ) Алгебраическое описание регулярных языков Grep Lex, Flex вход: РВ, выход: ДКА
- 26. Операции над языками 3. Итерация («звездочка», замыкание Клини – S. C. Kleene) языка L (L*) представляет
- 27. Построение РВ Базис: константы Ø и суть РВ, определяющие языки Ø и { } если a
- 28. Пример РВ для множества цепочек из чередующихся нулей и единиц 01 -> {01} (01)* -> {w:
- 29. Приоритеты операций РВ Замыкание Клини (применяется к наименьшей последовательности символов слева от нее и являющейся РВ)
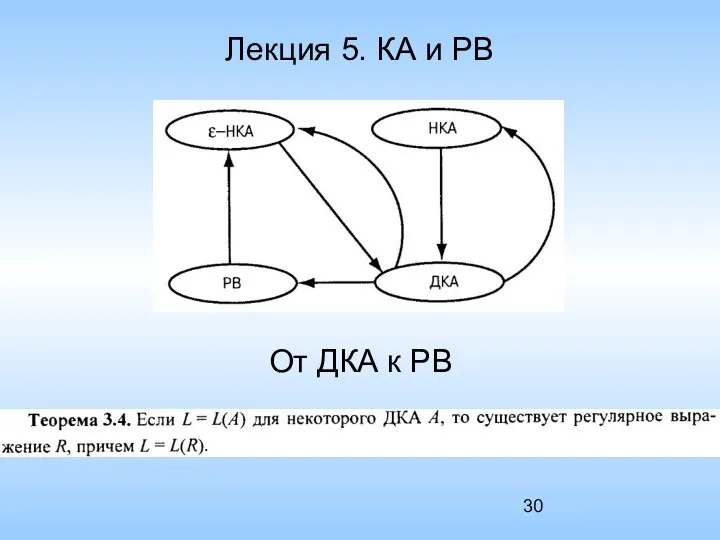
- 30. Лекция 5. КА и РВ От ДКА к РВ
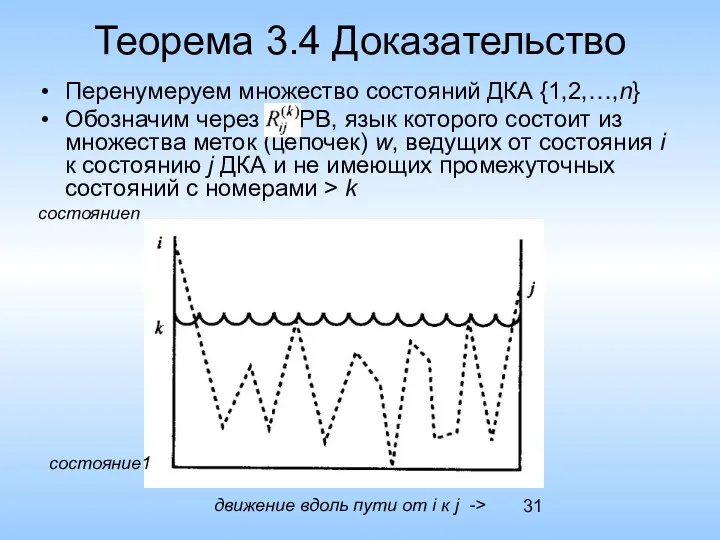
- 31. Теорема 3.4 Доказательство Перенумеруем множество состояний ДКА {1,2,…,n} Обозначим через РВ, язык которого состоит из множества
- 32. Теорема 3.4 Доказательство Для построения используем индуктивное определение от k=0 до k=n Базис: k=0 (у пути
- 34. Скачать презентацию





















 Ветвление в Паскале
Ветвление в Паскале Организация безопасности в компьютерных сетях образовательного учреждения
Организация безопасности в компьютерных сетях образовательного учреждения Формулы и методы планирования в Excel
Формулы и методы планирования в Excel Автоматизированная система оперативного управления перевозками (АСОУП)
Автоматизированная система оперативного управления перевозками (АСОУП)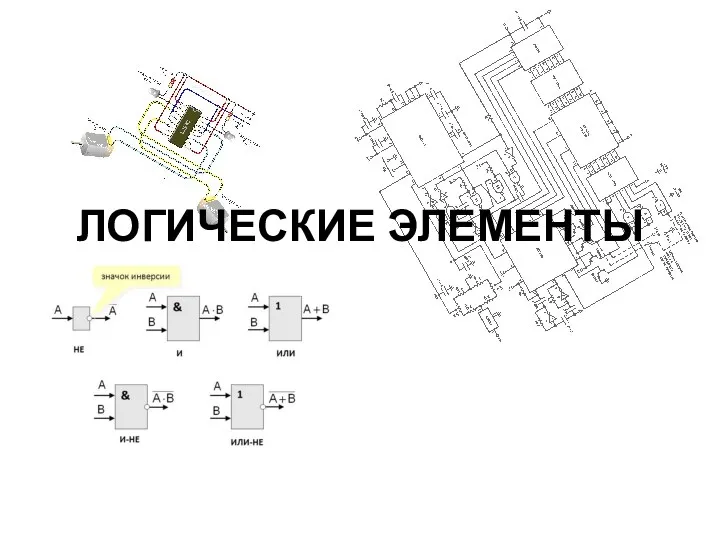 Логические элементы
Логические элементы 1С:Бухгалтерия сельскохозяйственного предприятия
1С:Бухгалтерия сельскохозяйственного предприятия Модель и моделирование. (10 класс)
Модель и моделирование. (10 класс) Голосовые ассистенты
Голосовые ассистенты Этапы создания (разработки) web-сайта
Этапы создания (разработки) web-сайта Елементи функціонального програмування
Елементи функціонального програмування Есептеуіш техниканың даму тарихы
Есептеуіш техниканың даму тарихы Тестирование программного обеспечения
Тестирование программного обеспечения Алгоритм и его формальное исполнение. Виды алгоритмов
Алгоритм и его формальное исполнение. Виды алгоритмов Основы электротехники. Платформа Arduino
Основы электротехники. Платформа Arduino Сеть платежных терминалов
Сеть платежных терминалов Збереження інформації
Збереження інформації Программирование на языке Python
Программирование на языке Python Электронная почта. Сетевое коллективное взаимодействие и сетевой этикет
Электронная почта. Сетевое коллективное взаимодействие и сетевой этикет Вирусы и антивирусы
Вирусы и антивирусы Информационная безопасность
Информационная безопасность Высказывания. Логические операции
Высказывания. Логические операции Ссылочные Биржи
Ссылочные Биржи Слой приложений
Слой приложений Правила использования сети интернет
Правила использования сети интернет Рекурсия. Для исполнителя Робот в системе программирования КУМИР
Рекурсия. Для исполнителя Робот в системе программирования КУМИР Виды графики. Компьютерная графика
Виды графики. Компьютерная графика Системы хранения данных (СХД). Перспективы развития. Лекция 14
Системы хранения данных (СХД). Перспективы развития. Лекция 14 Интернет-технологии в деятельности органов государственного управления
Интернет-технологии в деятельности органов государственного управления