Содержание
- 2. ПРОЦЕССЫ С ЦЕЛОЧИСЛЕННЫМИ ЗНАЧЕНИЯМИ пуассоновский процесс процесс размножения и гибели процесс чистого размножения распределение Пуассона марковская
- 3. Методика описания характеристик процессов с целочисленными значениями Вводятся постулаты процесса Строится автоматная модель (стохастический автомат Мура)
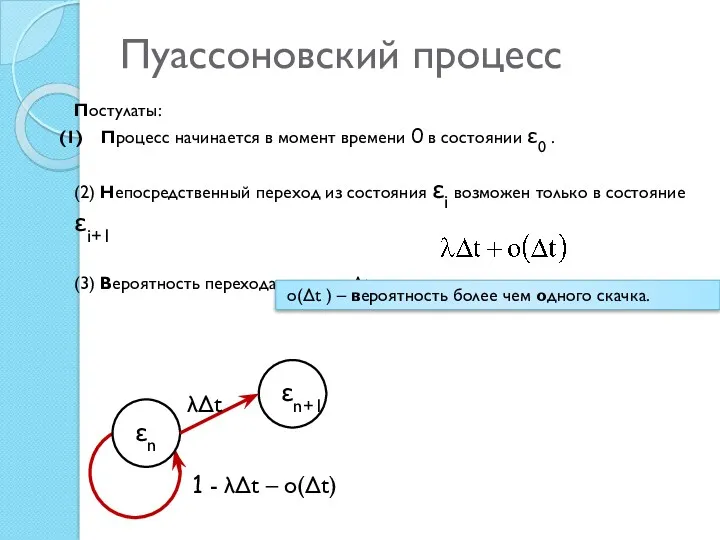
- 4. Пуассоновский процесс Постулаты: Процесс начинается в момент времени 0 в состоянии ε0 . (2) Непосредственный переход
- 5. Вероятности (находятся аналитически) Вероятность того, что система в момент времени (t + Δt) будет находиться в
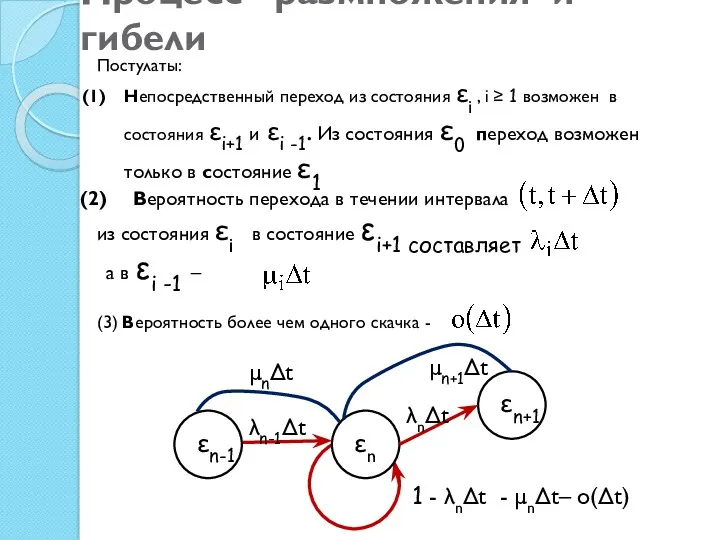
- 6. Процесс размножения и гибели Постулаты: Непосредственный переход из состояния εi , i ≥ 1 возможен в
- 7. Вероятности переходов Рис. 4.2. Фрагмент автоматной модели Состояние в момент времени возможно, если: (1) в момент
- 8. Вероятности состояний Начальные условия Условие стационарности Вероятности переходов в марковской сети
- 9. Процесс линейного роста Элементы совокупности на интервале могут делиться с вероятностью погибнуть с вероятностью
- 10. Распределение Пуассона Распределение Пуассона – распределение вероятностей случайной величины X с целочисленными неотрицательными значениями, заданное формулой
- 11. Пуассоновский процесс В теории случайных процессов при расчете нагрузки линий связи обычно полагают, что количество вызовов,
- 12. Марковская цепь Марковская цепь – важный пример последовательности зависимых случайных испытаний с конечным или счетным числом
- 13. Моделирование случайных потоков Рассматривается упорядоченная последовательность случайных моментов времени, в которые происходит или не происходит какое-либо
- 14. Типы потоков событий Потоки с ограниченным последействием, у которых интервалы статистически независимы, следовательно, многомерное распределение раскладывается
- 15. Методика моделирования случайных потоков (1) Формируются реализации случайных величин с заданным законом распределения (2) По формулам
- 16. ОЧЕРЕДИ Очередь в случае одного канала Предположение о показательном времени обслуживания Очереди с бесконечным числом каналов
- 17. Предположение о показательном времени обслуживания Простейший случай постоянных коэффициентов в процессе размножения и гибели Процесс размножения
- 18. Предположение о показательном времени обслуживания Представим, что решение продолжать или не продолжать разговор принимается каждую секунду
- 20. Скачать презентацию















 Labor Dynamics of the IT Economy. What IT Planners Need to Know about the Nature of Programming
Labor Dynamics of the IT Economy. What IT Planners Need to Know about the Nature of Programming Признаки объектов
Признаки объектов Обработка информации. Получение новой информации. 5 класс.
Обработка информации. Получение новой информации. 5 класс. Количественные параметры информационных объектов
Количественные параметры информационных объектов Поколения ЭВМ
Поколения ЭВМ Относительные, абсолютные и смешанные ссылки. 9 класс
Относительные, абсолютные и смешанные ссылки. 9 класс Условия и циклы языка ABAP
Условия и циклы языка ABAP Авантелеком - Цифровая платформа управления коммуникациями для государственных и муниципальных унитарных предприятий
Авантелеком - Цифровая платформа управления коммуникациями для государственных и муниципальных унитарных предприятий Путешествие в страну Инфознайка
Путешествие в страну Инфознайка Virtual reality
Virtual reality Презентация СAD-CAM-CAE-системы-назначение, виды, история
Презентация СAD-CAM-CAE-системы-назначение, виды, история Урок информатики Виды компьютерной графики
Урок информатики Виды компьютерной графики Развитие вычислительной техники и архитектура
Развитие вычислительной техники и архитектура CSS. Источники информации. Подключение CSS к HTML. Таблицы стилей для различных устройств просмотра. Селекторы и комбинаторы
CSS. Источники информации. Подключение CSS к HTML. Таблицы стилей для различных устройств просмотра. Селекторы и комбинаторы Моделирование на UML. Определение UML. Лекция 1
Моделирование на UML. Определение UML. Лекция 1 Программирование на языке Паскаль. Ветвления
Программирование на языке Паскаль. Ветвления Архивы, библиотеки, музеи в глобальной информационной среде
Архивы, библиотеки, музеи в глобальной информационной среде Развитие пошаговых стратегий
Развитие пошаговых стратегий Синхронизация. Критические секции (Critical section)
Синхронизация. Критические секции (Critical section) Разработка технологических карт уроков
Разработка технологических карт уроков Информационно - коммуникативные технологии в современной начальной школе.Презентация.
Информационно - коммуникативные технологии в современной начальной школе.Презентация. Базові засоби розробки і оформлення програм на мові Pascal
Базові засоби розробки і оформлення програм на мові Pascal Теоретические основы монтажа. Создание проекта в Adobe Premiere Pro
Теоретические основы монтажа. Создание проекта в Adobe Premiere Pro Основы программирования на Python
Основы программирования на Python Умный дом. Преимущества и возможности
Умный дом. Преимущества и возможности Решение задач. Basic
Решение задач. Basic Понятие информационного метода. Понятие информационного процесса
Понятие информационного метода. Понятие информационного процесса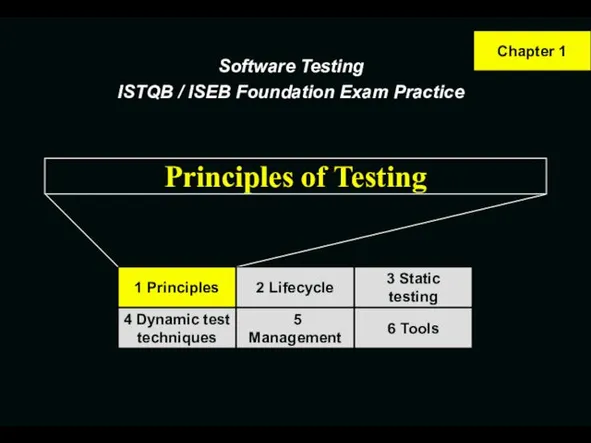 Principles of Testing
Principles of Testing