Содержание
- 2. Зміст навчальної дисципліни Статистичні методи аналізу даних ; Методи моделювання та аналізу взаємозвєязікв між характеристиками об’єкта
- 3. Лекція 1 Основні поняття математичної статистики Поняття вибіркового методу в статистиці Шкали вимірювань Статистичні ряди та
- 4. Математична статистика Математична статистика –розділ прикладної математики, предметом якого є розробка раціональних прийомів і методів отримання,
- 5. Генеральна сукупність та вибірка Сукупність об'єктів або спостережень, всі елементи якої підлягають вивченню при статистичному аналізі,
- 6. Генеральна сукупність та вибірка Вибірка вона повинна правильно відображати кількісні та якісні співвідношення генеральної сукупності, тобто
- 7. Шкали вимірювань Шкала − числова система, що відображає досліджувані властивості та ознаки об’єкта. Шкала найменувань (класифікації,
- 8. Статистичні ряди Припустимо, що необхідно вивчити деяку ознаку генеральної сукупності Х, для чого було проведено n
- 9. Ознака Х є випадковою величиною, а статистичний ряд – емпіричним (тобто отриманим у результаті експерименту або
- 10. Статистичні ряди Для побудови інтервального статистичного ряду множину значень варіант розбивають на інтервали , тобто проводять
- 11. Полігон частот, гістограма Полігоном частот (відносних частот) називається ламана лінія, що сполучає точки з координатами: (хi
- 12. Емпірична функція розподілу Емпірична функція розподілу і кумулята Кумулятою називається крива, що проходить через точки з
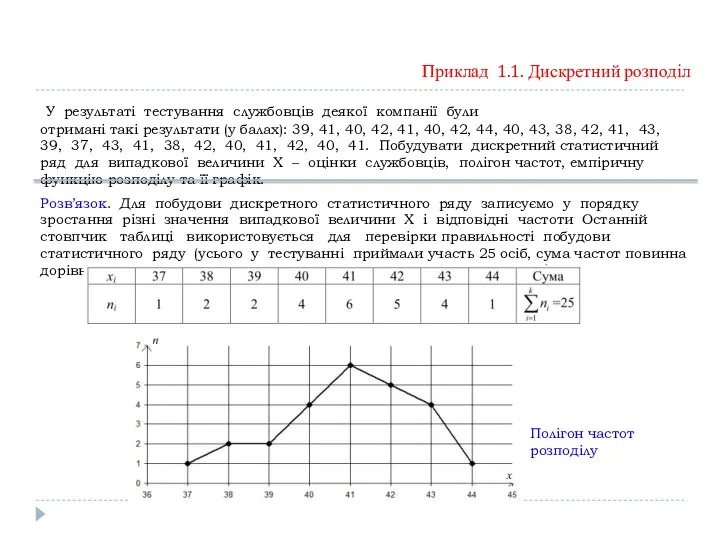
- 13. Приклад 1.1. Дискретний розподіл У результаті тестування службовців деякої компанії були отримані такі результати (у балах):
- 14. Для побудови емпіричної функції розподілу доповнимо таблицю двома рядками. В першому рядку обчислимо суму частот варіант,
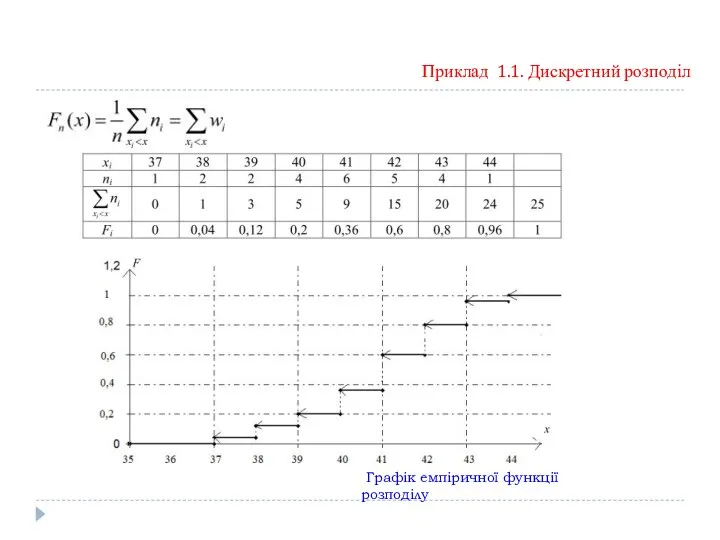
- 15. Приклад 1.1. Дискретний розподіл Графік емпіричної функції розподілу
- 16. Приклад 1.2. Неперервний розподіл За даними вибіркового дослідження було отримано розподіл родин за доходом на одного
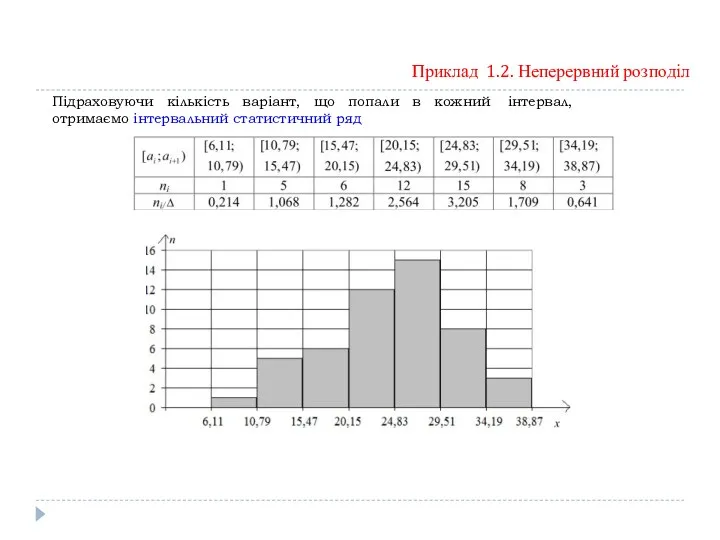
- 17. Приклад 1.2. Неперервний розподіл Підраховуючи кількість варіант, що попали в кожний інтервал, отримаємо інтервальний статистичний ряд
- 18. Приклад 1.2. Неперервний розподіл
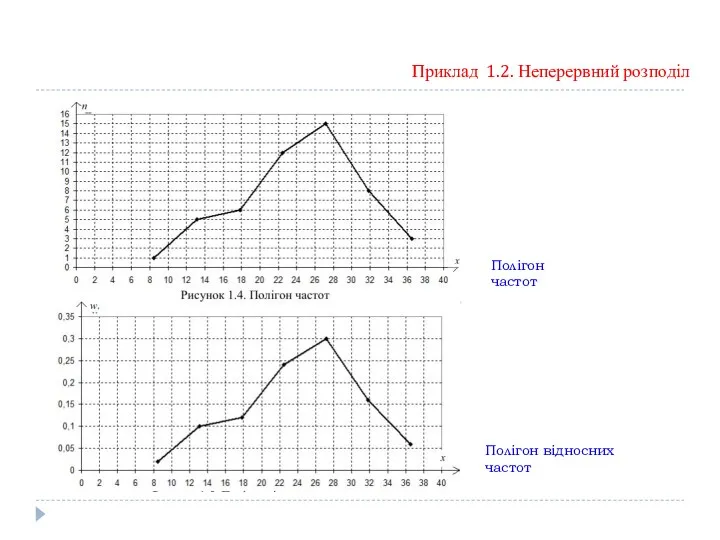
- 19. Приклад 1.2. Неперервний розподіл Полігон частот Полігон відносних частот
- 20. Приклад 1.2. Неперервний розподіл
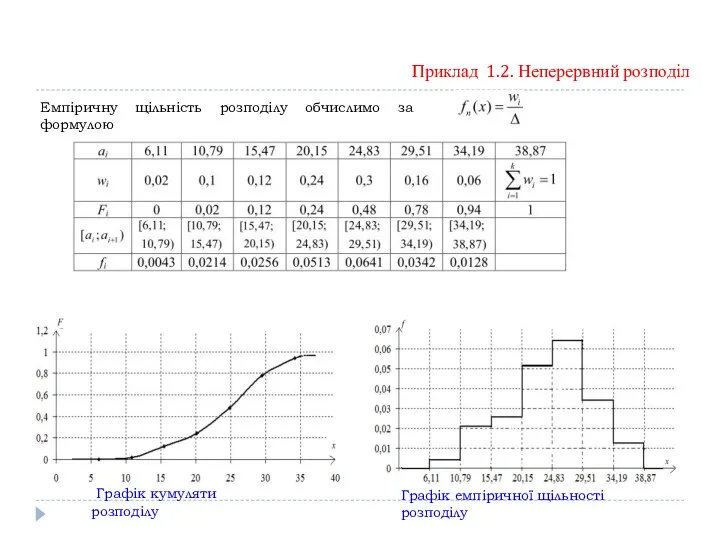
- 21. Емпіричну щільність розподілу обчислимо за формулою Приклад 1.2. Неперервний розподіл Графік кумуляти розподілу Графік емпіричної щільності
- 22. Числові характеристики статистичних рядів Деяку ознаку Х генеральної сукупності можна розглядати як випадкову величину. Числові характеристики
- 23. Числові характеристики статистичних рядів Медіаною Ме називається значення величини Х, що розділяє вибірку, елементи якої розташовані
- 24. Числові характеристики розсіювання Варіаційним розмахом R називається різниця між максимальним і мінімальним елементом вибірки: Вибірковою дисперсією
- 25. Вибіркове середнє квадратичне відхилення S - величина, що дорівнює кореню квадратному з вибіркової дисперсії: Числові характеристики
- 26. Приклад 1.3 За даними вибіркового дослідження відомі ціни хі певного товару у різних торгівельних організаціях. Знайти
- 27. Приклад 1.3
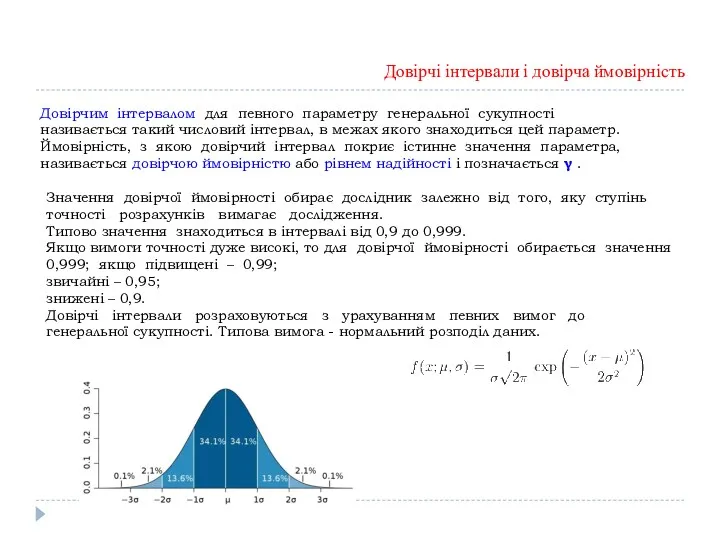
- 28. Довірчі інтервали і довірча ймовірність Довірчим інтервалом для певного параметру генеральної сукупності називається такий числовий інтервал,
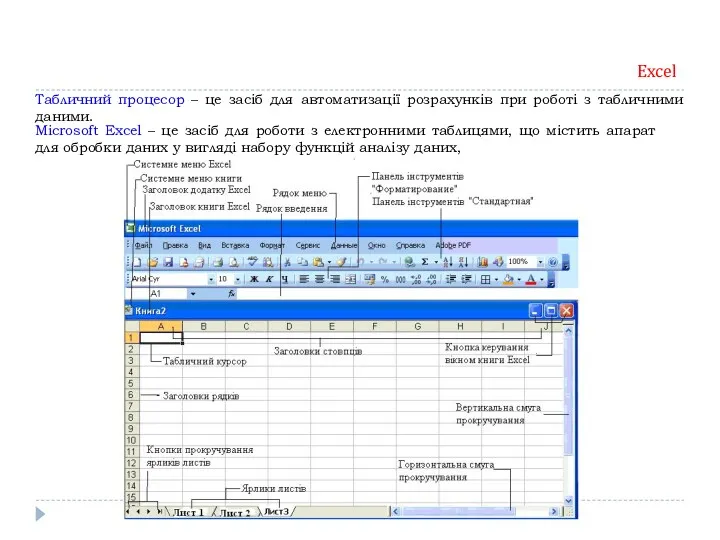
- 29. Excel Табличний процесор – це засіб для автоматизації розрахунків при роботі з табличними даними. Microsoft Excel
- 30. Робота з функціями Excel Функції – це заздалегідь визначені формули, що виконують обчислення за заданими величинами
- 31. Математичні функції СУММ – додає аргументи. КОРЕНЬ – повертає додатне значення квадратного кореня. COS, SIN, TAN
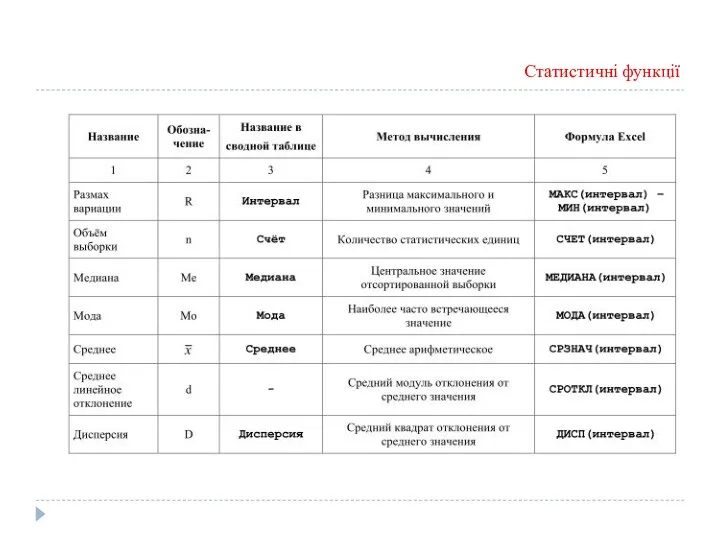
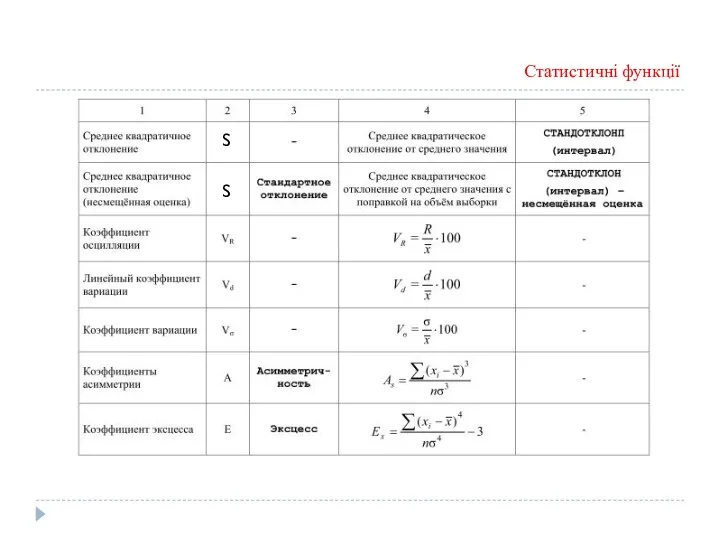
- 32. Статистичні функції
- 33. Статистичні функції S S
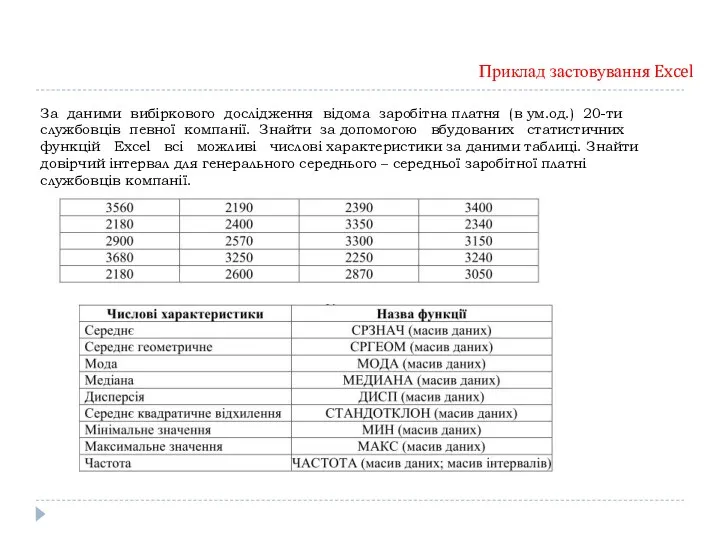
- 34. За даними вибіркового дослідження відома заробітна платня (в ум.од.) 20-ти службовців певної компанії. Знайти за допомогою
- 35. НОРМРАСП(x; a; σ; 0) НОРМРАСП(x; Среднее; Стандартное_откл; Интегральная), Статистичні функції НОРМРАСП(x; a; σ; 1) СТЬЮДРАСП(x; степени
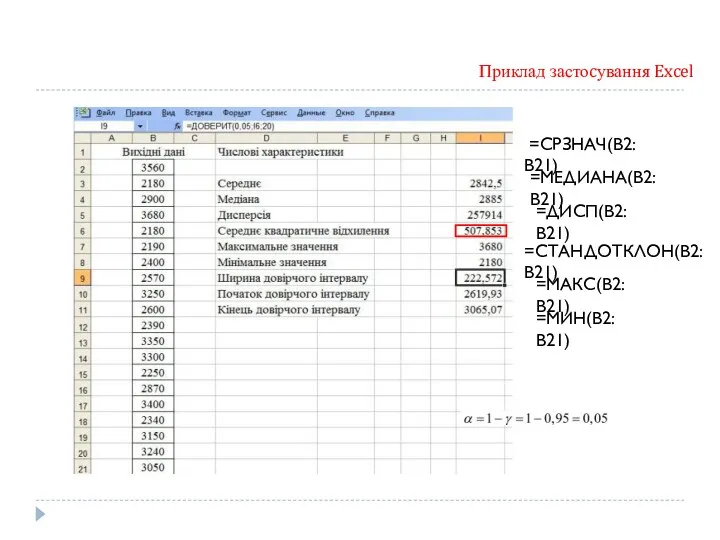
- 36. =СРЗНАЧ(В2:В21) =МЕДИАНА(В2:В21) =ДИСП(В2:В21) =СТАНДОТКЛОН(В2:В21) =МАКС(В2:В21) =МИН(В2:В21) Приклад застоcування Excel
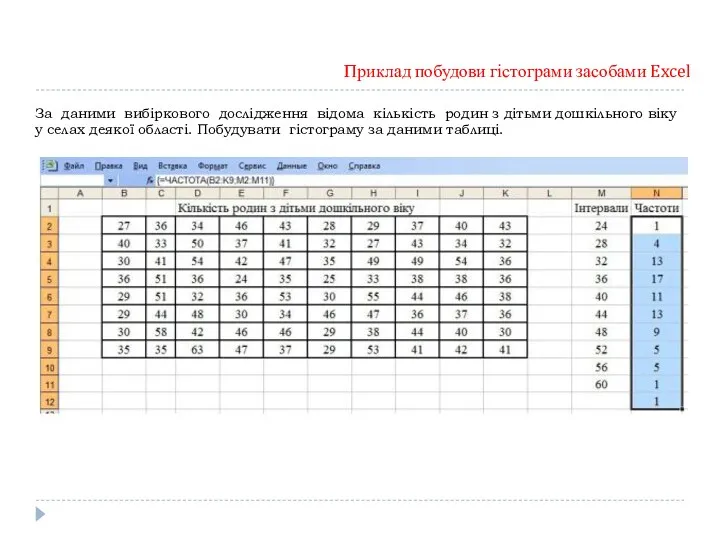
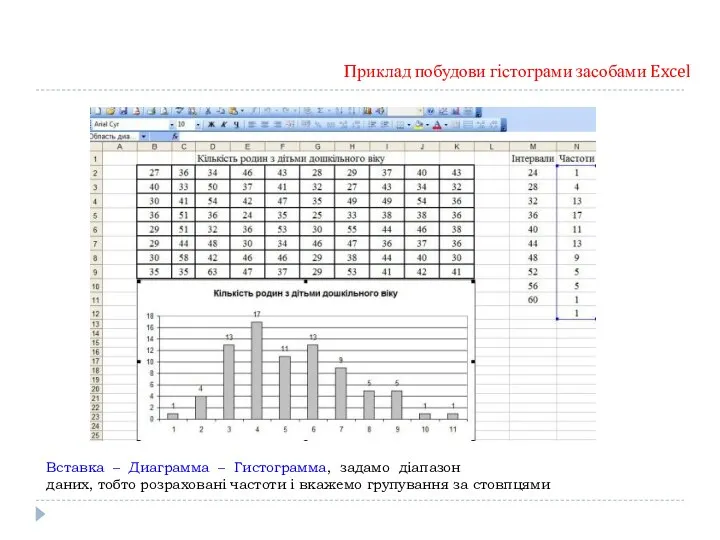
- 37. Приклад побудови гістограми засобами Excel За даними вибіркового дослідження відома кількість родин з дітьми дошкільного віку
- 38. Вставка – Диаграмма – Гистограмма, задамо діапазон даних, тобто розраховані частоти і вкажемо групування за стовпцями
- 39. Довірчий інтервал для генерального середнього при відомій генеральної дисперсії
- 40. Приклад 1.4
- 41. Довірчий інтервал для генерального середнього при невідомій генеральної дисперсії
- 42. Приклад 1.4
- 43. Довірчий інтервал для генеральної частки
- 44. Проведено вибірку об’ємом n = 2000 одиниць продукції. Серед обраних 150 одиниць виявилися бракованими. Знайти довірчий
- 45. Лекція 2 Статистичні гіпотези Поняття про статистичні гіпотези Перевірка гіпотези про вид закону розподілу досліджуваної величини
- 46. Статистичною гіпотезою називається будь-яке припущення про властивості досліджуваної величини, висунуте на основі статистичних даних. Типи статистичних
- 47. Якщо сформульовані гіпотези Н0 – основна та Н1 альтернативна (конкуруюча) і обраний критерій перевірки справедливості основної
- 48. Перевірка статистичних гіпотез здійснюється за такою послідовністю : 1) Висунення припущень про вид розподілу досліджуваної величини
- 49. Перевірка гіпотези про вид закону розподілу досліджуваної величини Перевірка гіпотези про вид закону розподілу досліджуваної величини
- 50. При здійсненні такої заміни немає впевненості, що закон розподілу обраний правильно. Розроблено процедуру, яка дозволяє оцінити
- 51. Перевірка гіпотези про закон розподілу величини Х здійснюється за етапами: 1) З генеральної сукупності Х формується
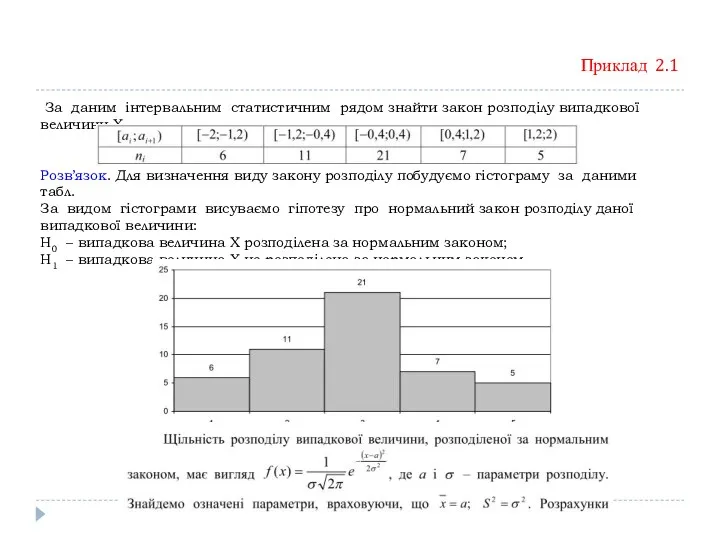
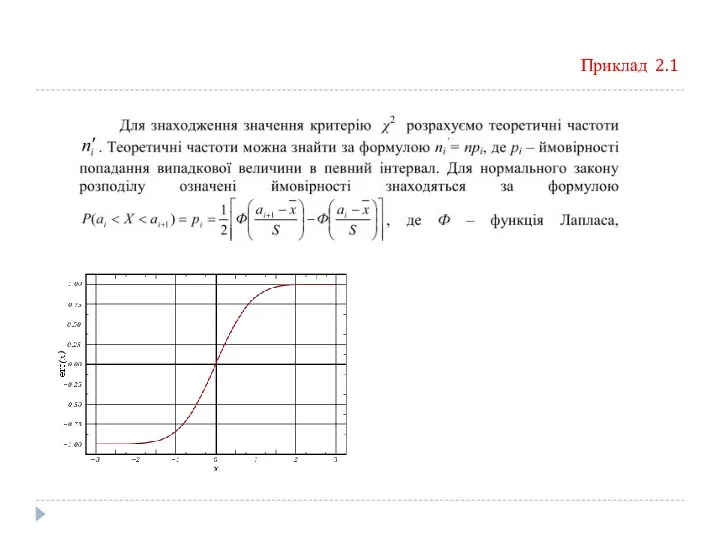
- 52. Приклад 2.1 За даним інтервальним статистичним рядом знайти закон розподілу випадкової величини Х Розв’язок. Для визначення
- 53. Знайдемо вибіркове середнє, вибіркову дисперсію і вибіркове середнє квадратичне відхилення Приклад 2.1
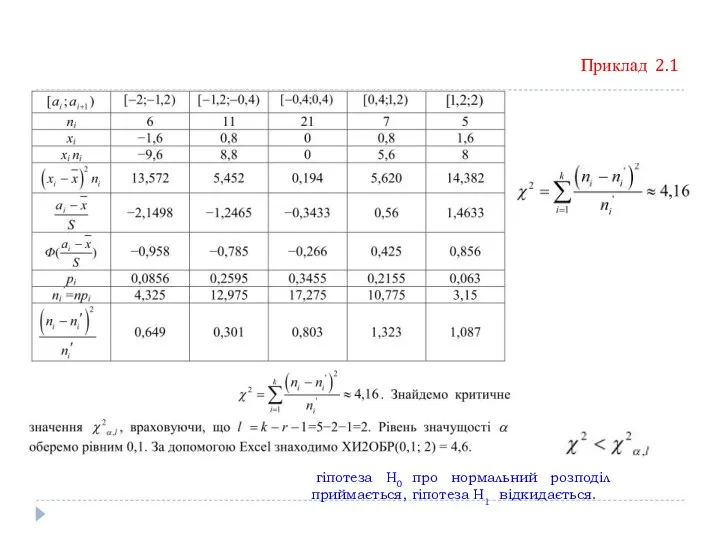
- 54. Приклад 2.1
- 55. Приклад 2.1 гіпотеза Н0 про нормальний розподіл приймається, гіпотеза Н1 відкидається.
- 56. Перевірка гіпотез про генеральні середні і дисперсії В прикладних задачах часто виникає необхідність перевірки рівності середніх
- 57. Перевірка гіпотези про рівність генеральних дисперсій. F-критерій (Фішера)
- 58. Приклад 2.2 Відомо дані про продуктивність праці (одиниць продукції за зміну) двох груп працівників: група 1
- 59. Приклад 2.2
- 60. Перевірка гіпотези про рівність генеральних дисперсій. Критерій Зігеля-Тьюкі Якщо статистичні дані не розподілені за нормальним законом
- 61. Перевірка гіпотези про рівність генеральних дисперсій. Критерій Зігеля-Тьюкі
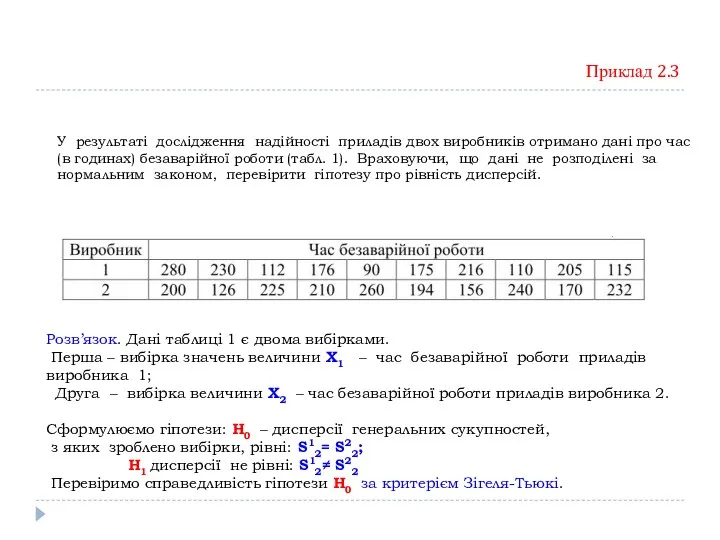
- 62. Приклад 2.3 У результаті дослідження надійності приладів двох виробників отримано дані про час (в годинах) безаварійної
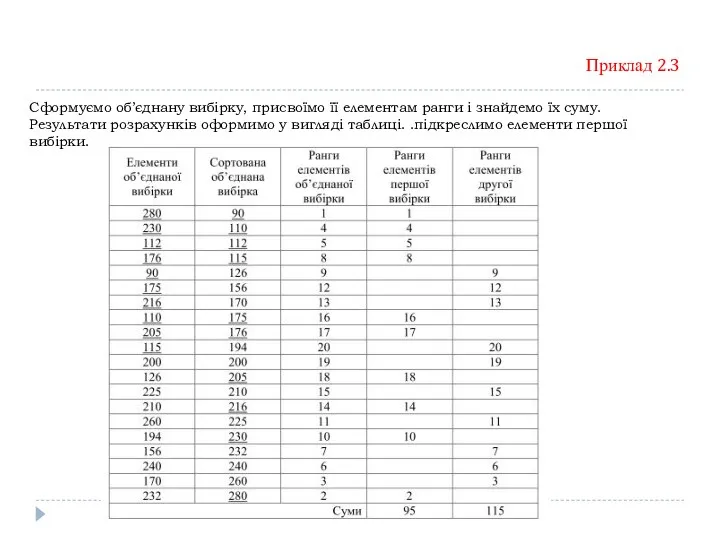
- 63. Приклад 2.3 Сформуємо об’єднану вибірку, присвоїмо її елементам ранги і знайдемо їх суму. Результати розрахунків оформимо
- 64. Приклад 2.3 Розрахуємо за формулою значення нормальної випадкової величини Z, враховуючи, що n1= n2= 10
- 65. Перевірка гіпотези про рівність генеральних середніх. Критерій Стьюдента Критерій Стьюдента використовується для перевірки гіпотез про рівність
- 66. Перевірка гіпотези про рівність генеральних середніх. Критерій Стьюдента
- 67. Перевірка гіпотези про рівність генеральних середніх. Критерій Стьюдента
- 68. Приклад 2.4 Для виробництва кожної з 10 деталей за першою технологією було витрачено, у середньому, 30
- 69. Приклад 2.4
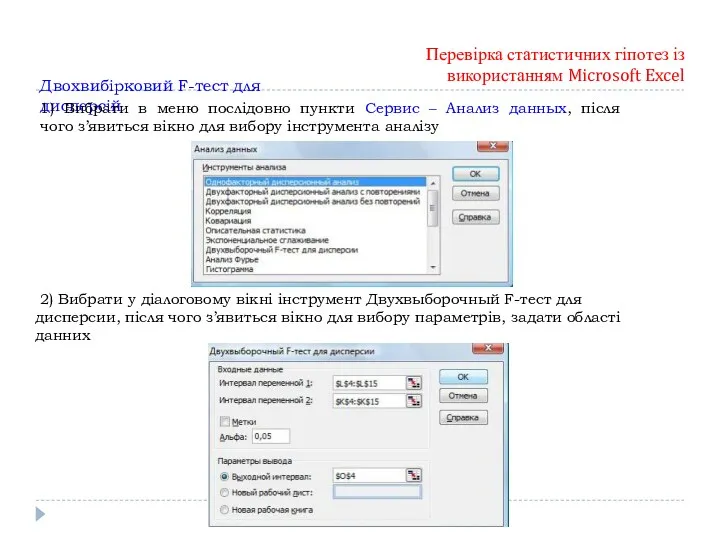
- 70. Перевірка статистичних гіпотез із використанням Microsoft Excel Двохвибірковий F-тест для дисперсій 1) Вибрати в меню послідовно
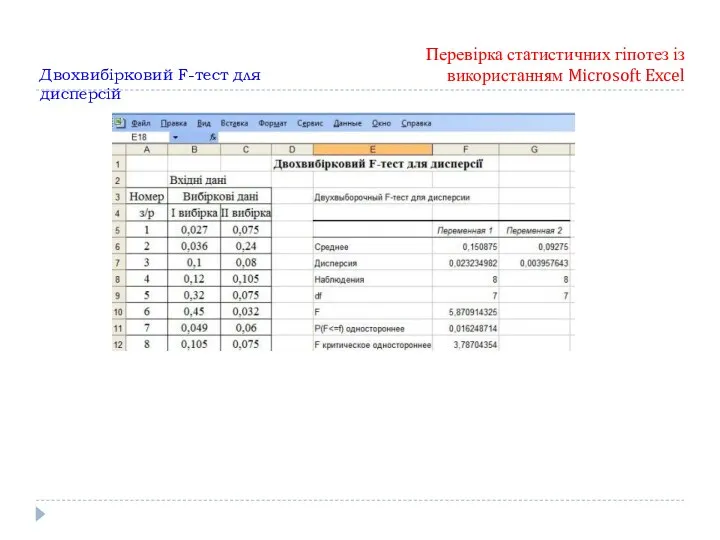
- 71. Перевірка статистичних гіпотез із використанням Microsoft Excel Двохвибірковий F-тест для дисперсій
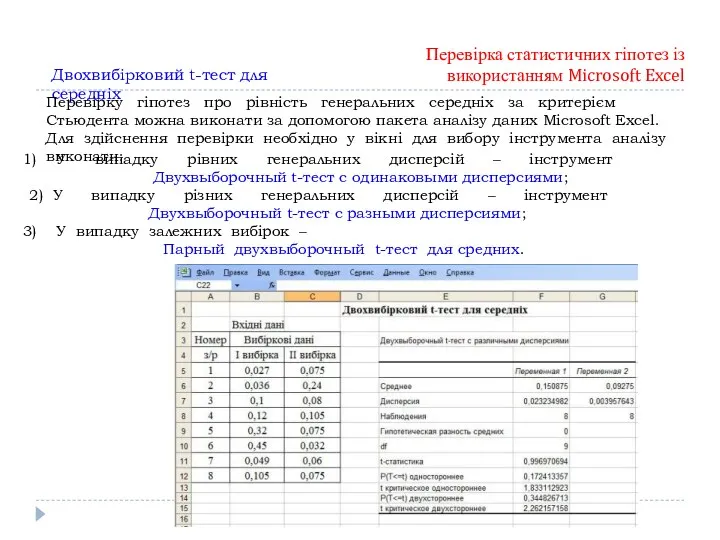
- 72. Двохвибірковий t-тест для середніх Перевірка статистичних гіпотез із використанням Microsoft Excel Перевірку гіпотез про рівність генеральних
- 73. Лекція 3 Основи кореляційного аналізу Поняття кореляційного зв’язку між досліджуваними величинами. Групування даних для кореляційного аналізу
- 74. Кореляційний аналіз - математичний апарат для виявлення зв’язків і оцінки їх сили (тісноти) між ознаками різних
- 75. Якщо кожному значенню факторної ознаки Х відповідає безліч значень результативної ознаки Y, то говорять, що між
- 76. Якщо кожному значенню факторної ознаки Х відповідає певне середнє значення результативної ознаки Y, то говорять, що
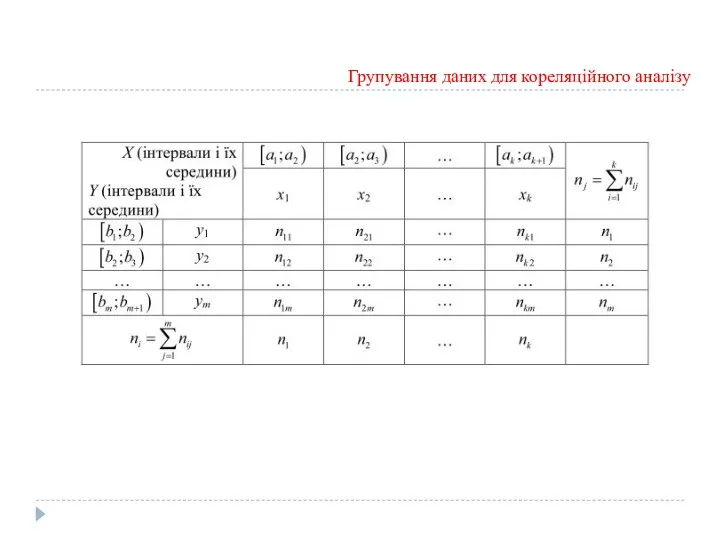
- 77. Групування даних для кореляційного аналізу
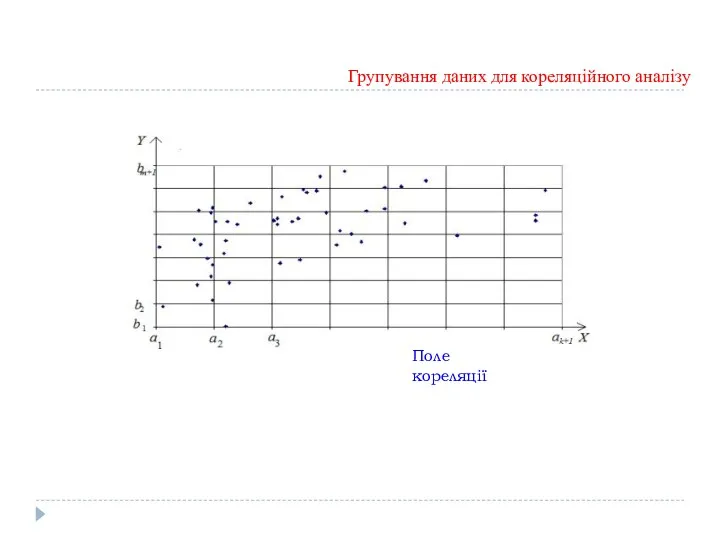
- 78. Групування даних для кореляційного аналізу Поле кореляції
- 79. Групування даних для кореляційного аналізу
- 80. Групування даних для кореляційного аналізу
- 81. Групування даних для кореляційного аналізу
- 82. Коефіцієнт кореляції Пірсона
- 83. Коефіцієнт кореляції Пірсона
- 84. Коефіцієнт кореляції Пірсона
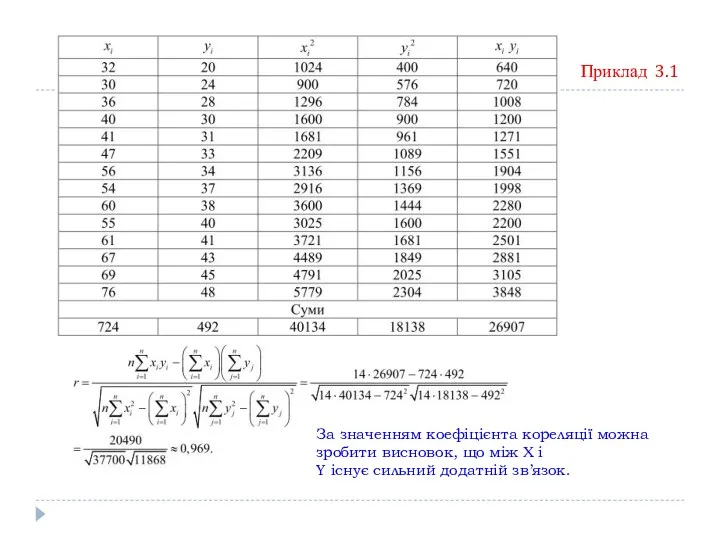
- 85. Приклад 3.1 За наявними даними про рівнем оплати праці Х і продуктивності праці Y для 14
- 86. Приклад 3.1 За значенням коефіцієнта кореляції можна зробити висновок, що між Х і Y існує сильний
- 87. Перевіримо статистичну значущість знайденого коефіцієнта кореляції Пірсона. Розрахуємо t-статистику за формулою Приклад 3.1 Висновок. Між рівнем
- 88. Коефіцієнт кореляції Спірмена Статистична значущість коефіцієнта кореляції Спірмена перевіряється так, як і коефіцієнта кореляції Пірсона.
- 89. Вивчається залежність між продуктивністю праці робітників Х (тис. грн.) та їх емоційним відношенням до своєї професійної
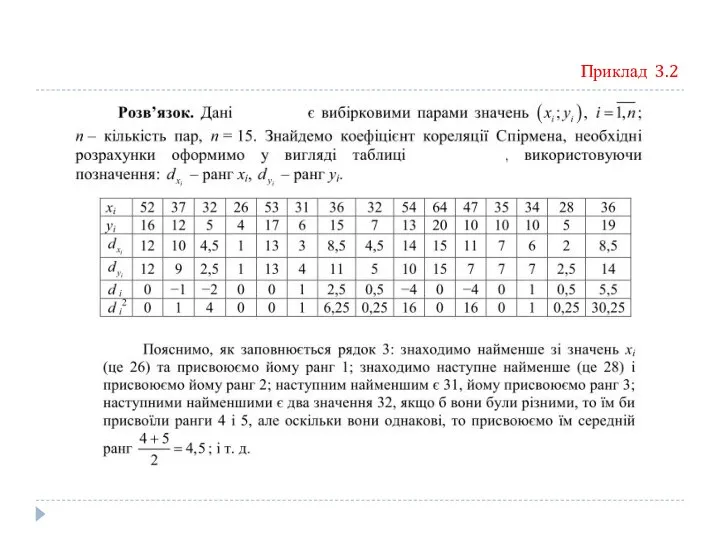
- 90. Приклад 3.2
- 91. Приклад 3.2
- 92. Приклад 3.2 Висновок. Між продуктивністю праці та емоційним відношенням працівника до професійної діяльності існує сильний додатній
- 93. Множинний та частинний коефіцієнти кореляції
- 94. Множинний та частинний коефіцієнти кореляції
- 95. Множинний та частинний коефіцієнти кореляції
- 96. Множинний та частинний коефіцієнти кореляції
- 97. Для вивчення залежності отриманого доходу Z від мотивованості працівників Х (бали) і величини інвестицій Y було
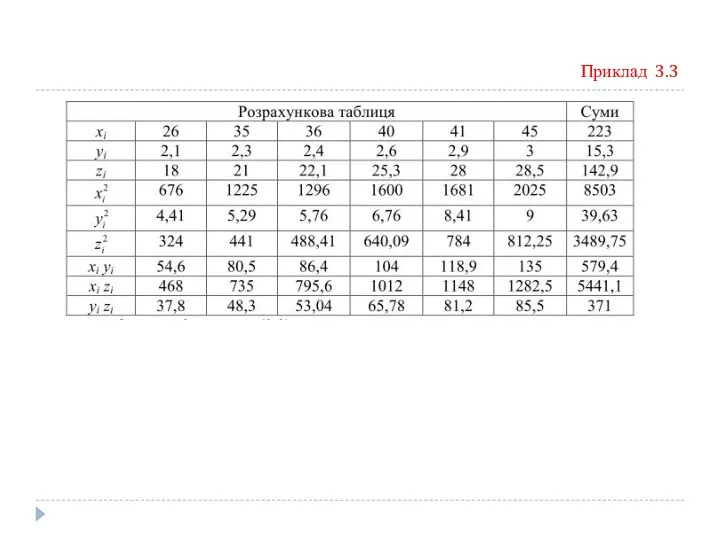
- 98. Приклад 3.3
- 99. Приклад 3.3
- 100. Приклад 3.3
- 101. Приклад 3.3+ правило Саррюса
- 102. Перевіримо статистичну значущість множинного коефіцієнта кореляції RZ . Знайдемо t-статистику за формулою Приклад 3.3
- 103. Приклад 3.3 Для обчислення частинних коефіцієнтів кореляції Знайдемо t-статистику
- 104. Висновок: отриманий дохід залежить від мотивованості працівників та величини інвестицій. При цьому дохід значно сильніше залежить
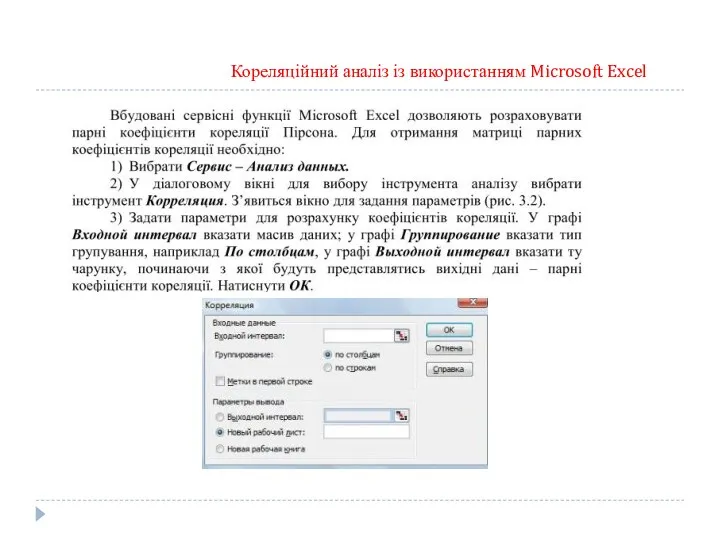
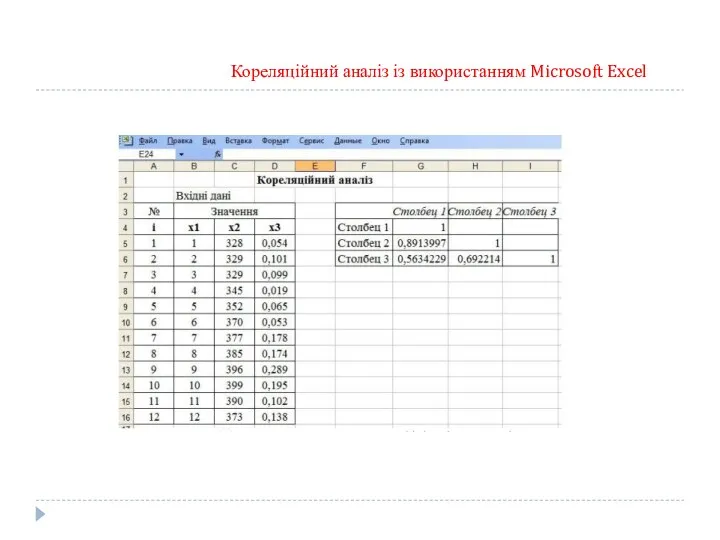
- 105. Кореляційний аналіз із використанням Microsoft Excel
- 106. Кореляційний аналіз із використанням Microsoft Excel
- 107. Лекція 5 Побудова регресійних моделей Встановлення виду кореляційної залежності Лінійна регресія Нелінійна регресія Множинна лінійна регресія
- 108. Регресійний аналіз
- 109. Встановлення виду кореляційної залежності
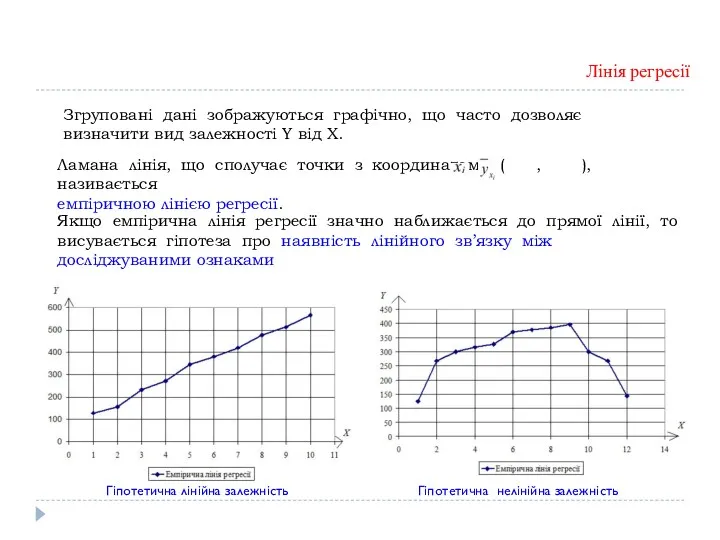
- 110. Згруповані дані зображуються графічно, що часто дозволяє визначити вид залежності Y від Х. Ламана лінія, що
- 111. Лінійна регресія Побудова лінійної регресійної моделі – це знаходження параметрів рівняння . Параметри рівняння регресії можна
- 112. Метод найменших квадратів Якщо вибіркові дані не згруповані, то система спрощується:
- 113. Метод найменших квадратів
- 114. Метод найменших квадратів
- 115. Метод найменших квадратів
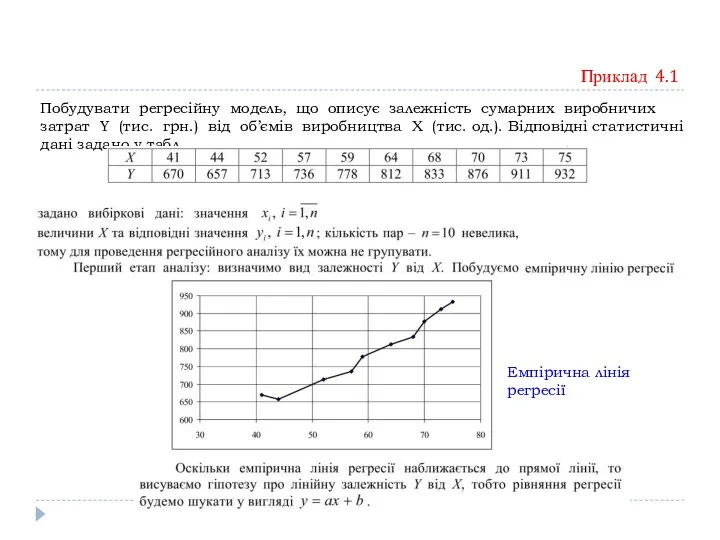
- 116. Побудувати регресійну модель, що описує залежність сумарних виробничих затрат Y (тис. грн.) від об’ємів виробництва Х
- 117. Приклад 4.1
- 118. Приклад 4.1
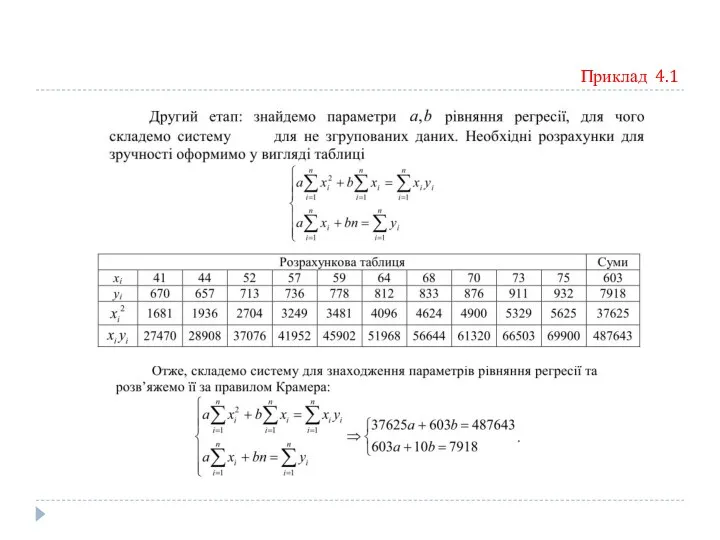
- 119. Приклад 4.1
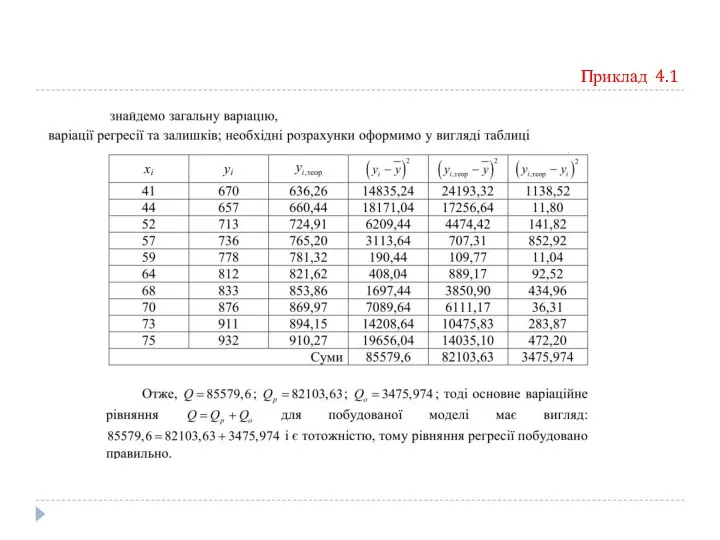
- 120. Приклад 4.1
- 121. Приклад 4.1
- 122. Нелінійна регресія
- 123. Нелінійна регресія
- 124. Нелінійна регресія
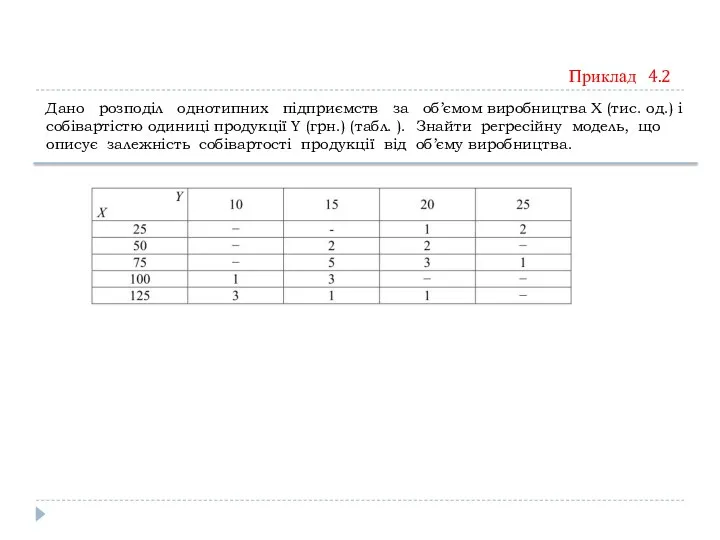
- 125. Приклад 4.2 Дано розподіл однотипних підприємств за об’ємом виробництва Х (тис. од.) і собівартістю одиниці продукції
- 126. Розв’язок. Для проведення регресійного аналізу за даними табл. побудуємо кореляційну таблицю Приклад 4.2
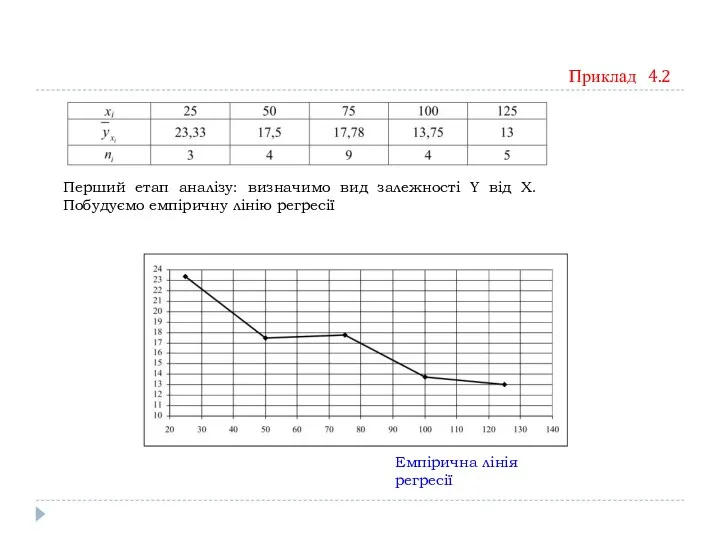
- 127. Приклад 4.2 Перший етап аналізу: визначимо вид залежності Y від Х. Побудуємо емпіричну лінію регресії Емпірична
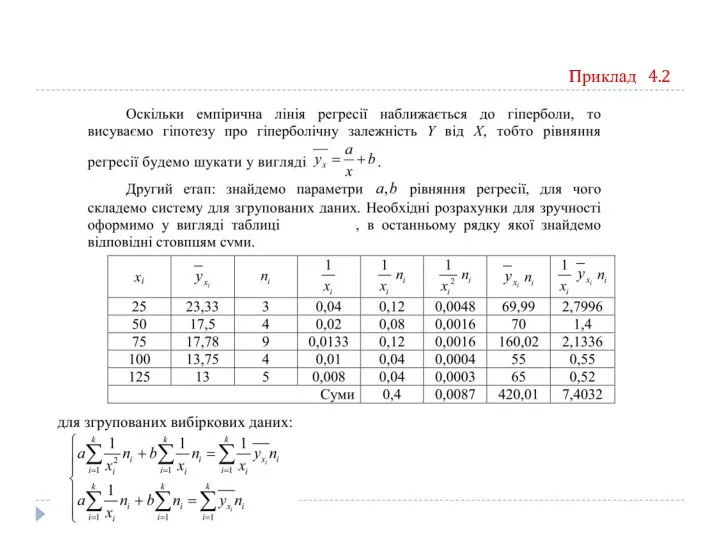
- 128. Приклад 4.2
- 129. Отже, складемо систему для знаходження параметрів рівняння регресії та розв’яжемо її за правилом Крамера: Приклад 4.2
- 130. Приклад 4.2
- 131. Приклад 4.2
- 132. Множинна лінійна регресія
- 133. Множинна лінійна регресія
- 134. Множинна лінійна регресія
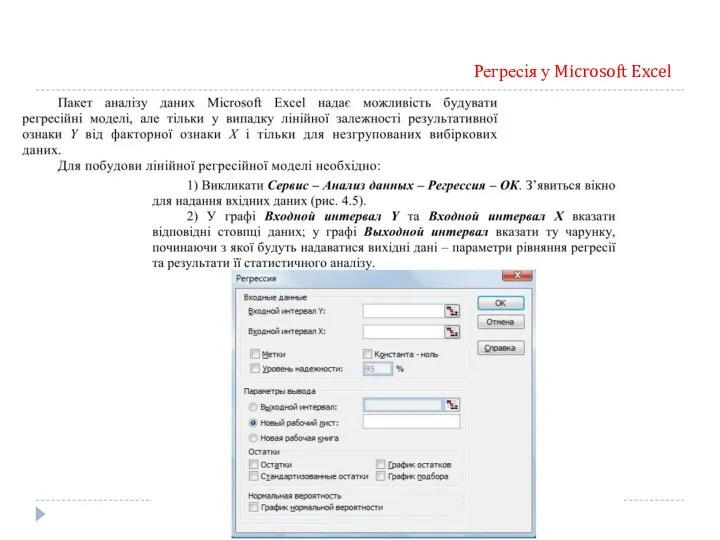
- 135. Регресія у Microsoft Excel
- 136. Регресія у Microsoft Excel Результати регресійного аналізу
- 137. Регресія у Microsoft Excel
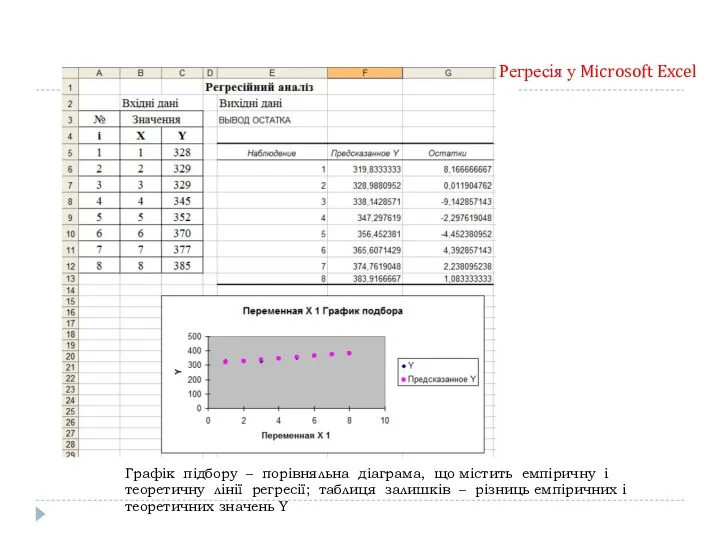
- 138. Графік підбору – порівняльна діаграма, що містить емпіричну і теоретичну лінії регресії; таблиця залишків – різниць
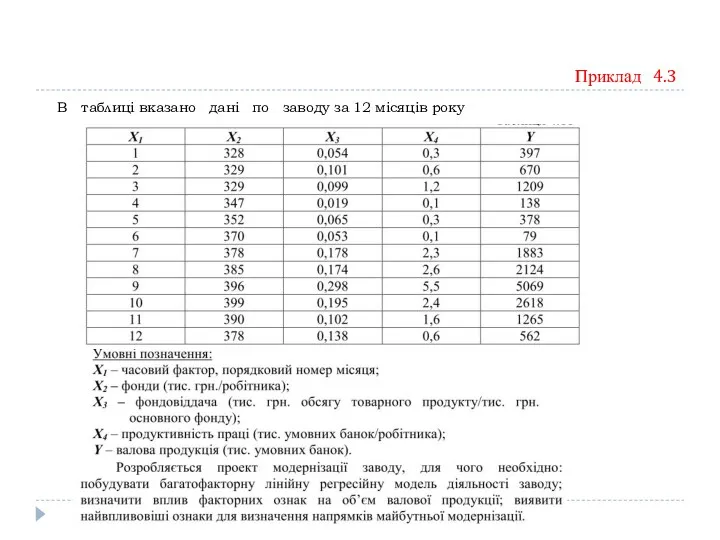
- 139. Приклад 4.3 В таблиці вказано дані по заводу за 12 місяців року
- 140. Приклад 4.3
- 141. Приклад 4.3 Отримаємо табл., яка є матрицею парних коефіцієнтів кореляції. Чарунки таблиці, розташовані вище головної діагоналі,
- 142. Виділимо в таблиці елементи, які більші за rкр (це означає, що відповідні ознаки тісно пов’язані між
- 143. За результатами аналізу кореляційної матриці побудуємо кореляційні плеяди, тобто зобразимо достовірний зв’язок між факторними ознаками графічно
- 144. Приклад 4.3
- 145. Приклад 4.3
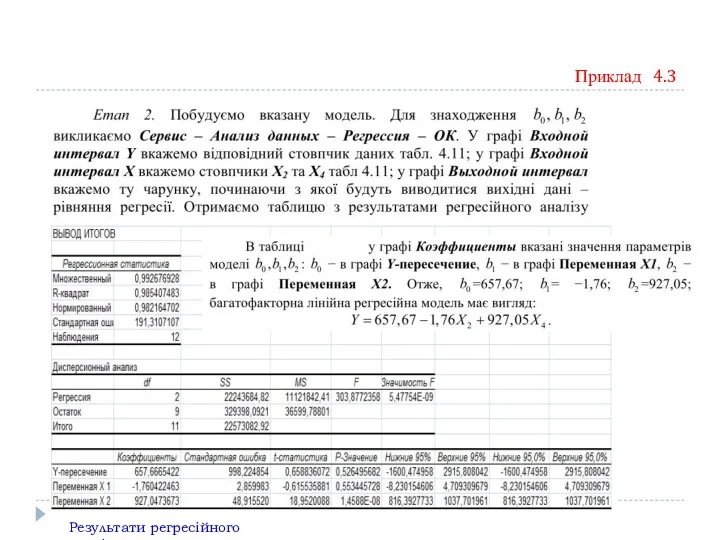
- 146. Приклад 4.3 Результати регресійного аналізу
- 147. Приклад 4.3
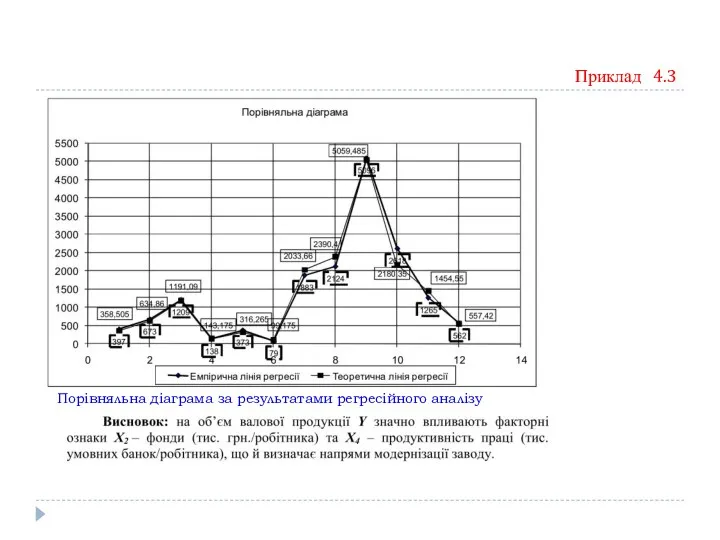
- 148. Порівняльна діаграма за результатами регресійного аналізу Приклад 4.3
- 149. Лекція 6 Ряди динаміки. аналіз інтенсивності та тенденцій розвитку Суть та складові елементи ряду динаміки. Види
- 150. Суть та складові елементи ряду динаміки В статистичній практиці доводиться мати справу з великою кількістю даних,
- 151. Види динамічних рядів В залежності від характеру рівнів ряду розрізняють види рядів динаміки: моментні і інтервальні
- 152. Статистичні дані, які необхідні для побудови ряду динаміки повинні бути порівняльні за колом охоплюваних об'єктів. Непорівняльність
- 153. Приклад
- 154. Основні показники рядів динаміки Завдання - шляхом аналізу рядів динаміки розкрити і охарактеризувати закономірності, що проявляються
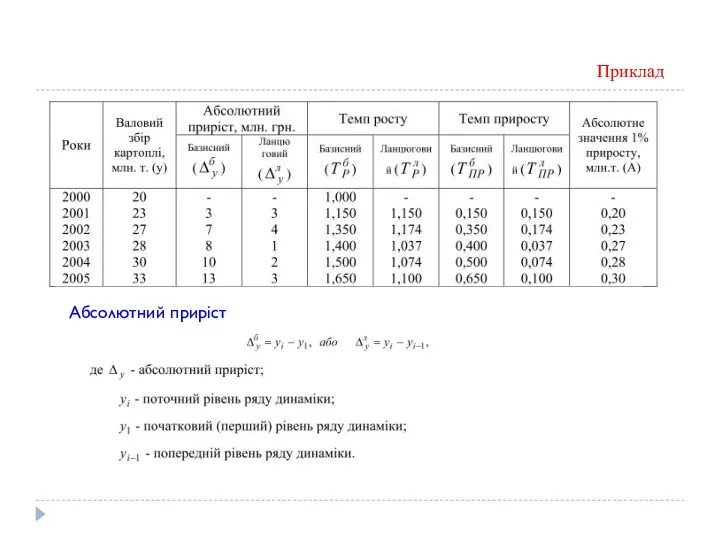
- 155. Абсолютний приріст Абсолютний приріст (Δ) обчислюється як різниця між поточним та базисним рівнями і показує, на
- 156. Приклад Абсолютний приріст
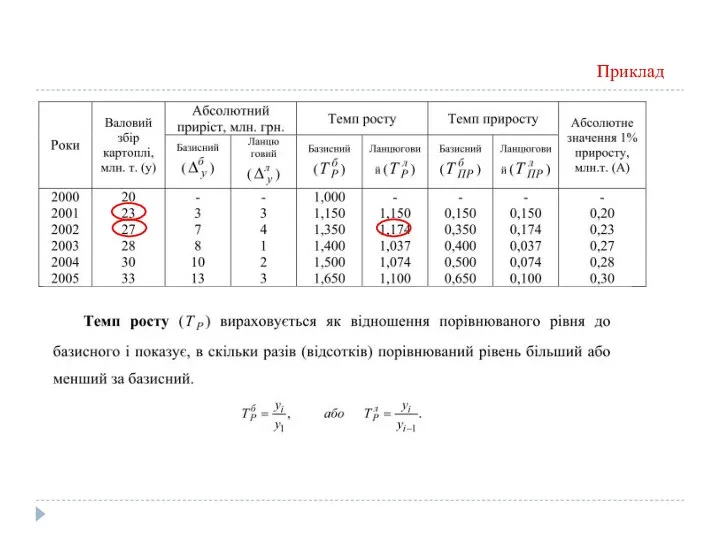
- 157. Коефіцієнт зростання Коефіцієнт зростання (Кр) вираховується як відношення порівнюваного рівня до базисного і показує, в скільки
- 158. Приклад
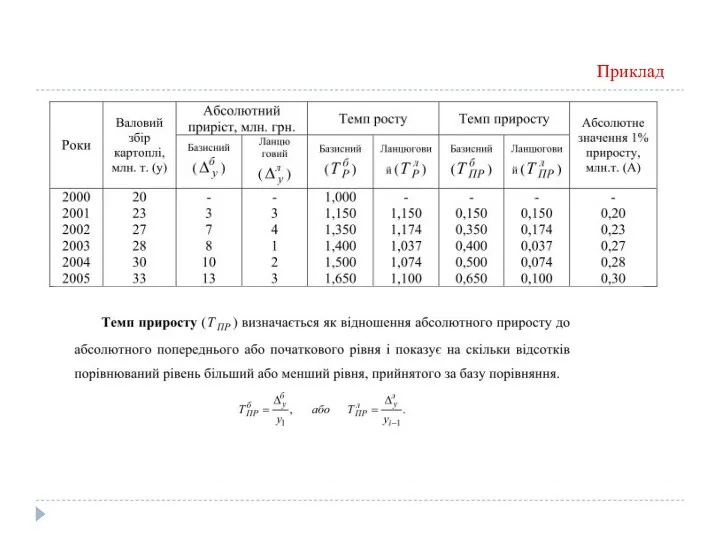
- 159. Темп приросту Темп приросту (Тпр) визначається як відношення абсолютного приросту до абсолютного попереднього або початкового рівня
- 160. Приклад
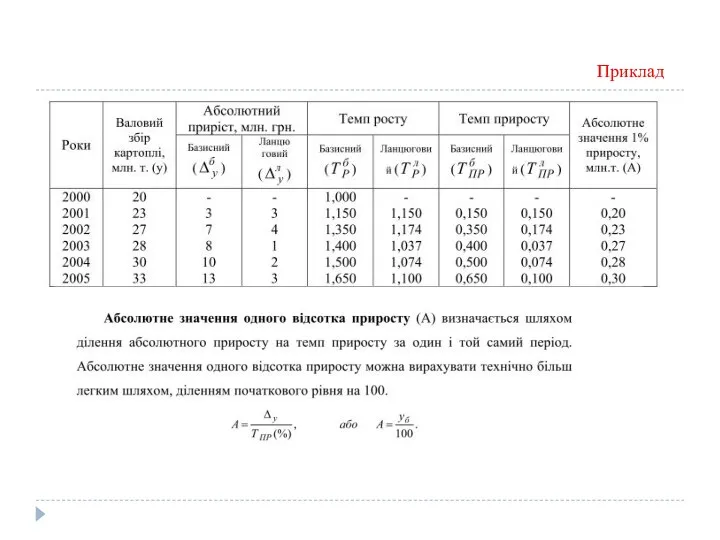
- 161. Абсолютне значення одного відсотка приросту. Абсолютне значення одного відсотка приросту (А) визначається шляхом ділення абсолютного приросту
- 162. Приклад
- 163. Взаємозвязки. Абсолютне та відносне прискорення Ланцюгові й базисні характеристики динаміки взаємопов’язані: 1) сума ланцюгових абсолютних приростів
- 164. Середні показники динаміки Динамічні ряди складаються з багатьох варіаційних рівнів тому потребують узагальнюючих характеристик. Середні показники:
- 165. Середній абсолютний приріст визначається як середня арифметичне з ланцюгових абсолютних приростів за певні періоди і показує
- 166. Приклад Кількість працівників ПНУ в січні 2015 р
- 167. Приклад Динаміка зміни кількость тракторів в парку агрофірми за 2014 рік середнє хронологічне
- 168. Виявлення тенденцій розвитку явищ Виявлення основної тенденції (тренду) ряду, є одним з головних методів аналізу і
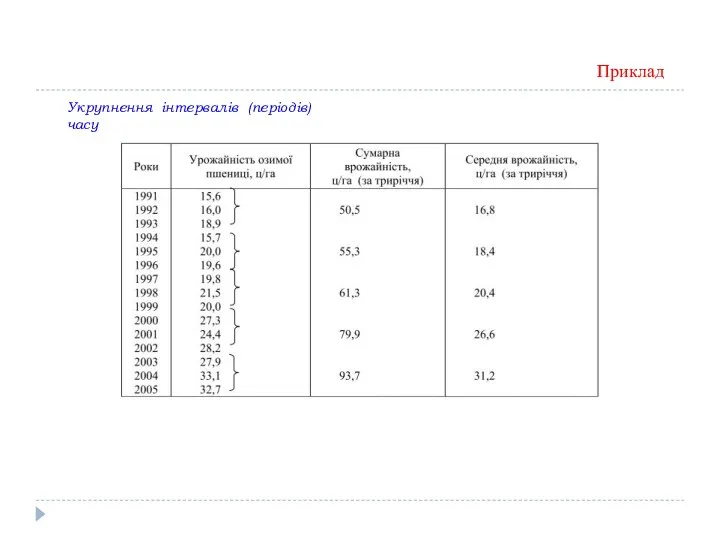
- 169. Укрупнення інтервалів (періодів) часу Приклад
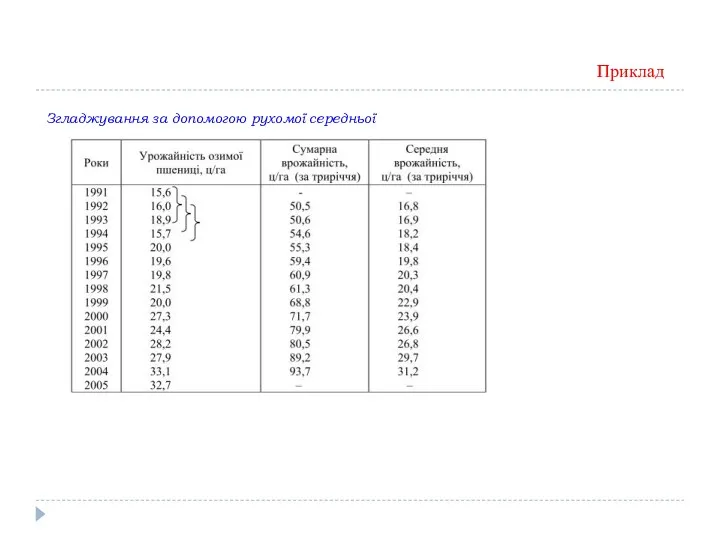
- 170. Згладжування за допомогою рухомої середньої Приклад
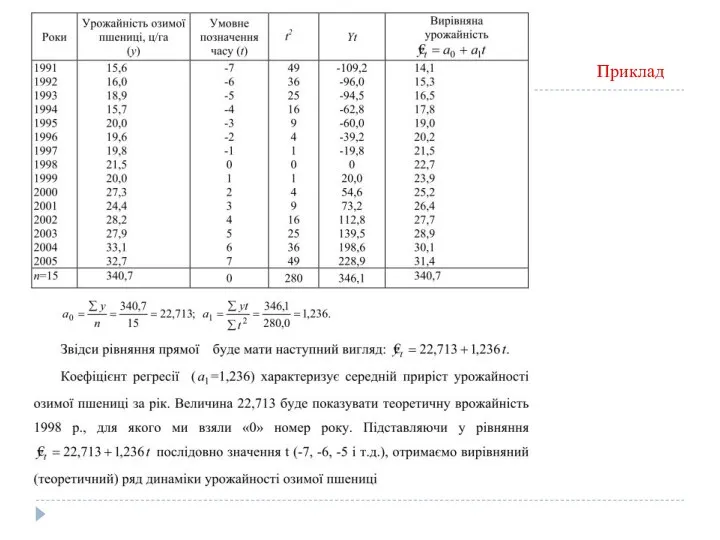
- 171. Аналітичне вирівнювання Вирівнювання за прямою використовується в тих випадках, коли абсолютні прирости приблизно постійні, тобто коли
- 172. Приклад
- 173. Приклад
- 174. Характеристика сезонних коливань, методи їх вимірювання Сезонними коливаннями називаються стійкі внутрішньорічні коливання в рядах динаміки, обумовлені
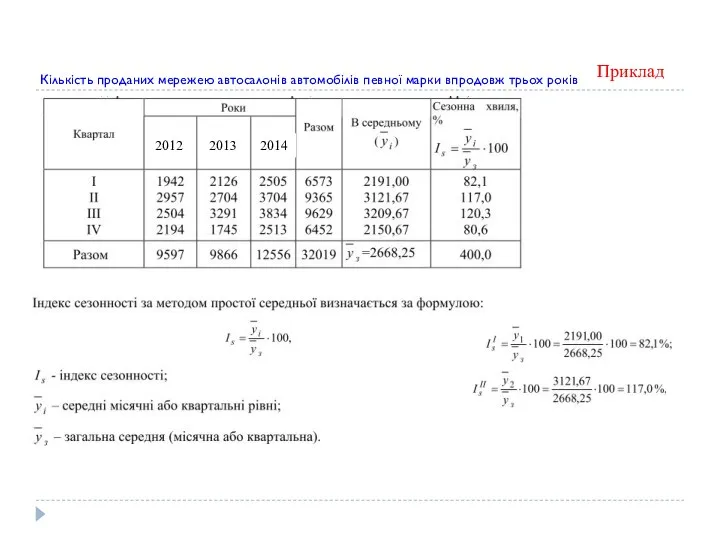
- 175. Приклад Кількість проданих мережею автосалонів автомобілів певної марки впродовж трьох років
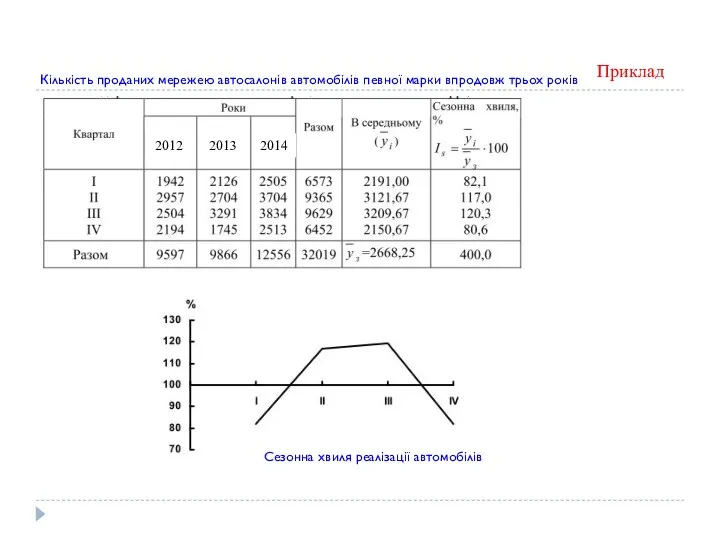
- 176. Приклад Кількість проданих мережею автосалонів автомобілів певної марки впродовж трьох років Сезонна хвиля реалізації автомобілів
- 177. Лекція 7 Індекси Суть та функції індексів у статистичному дослідженні. Види індексів. Методологічні принципи побудови агрегатних
- 178. Для характеристики соціально-економічних явищ і процесів статистика використовує узагальнюючі показники у вигляді середніх, відносних величин та
- 179. Суть та функції індексів у статистичному дослідженні Друга сфера застосування індексів полягає у їх використанні для
- 180. Всі економічні індекси статистика класифікує за трьома основними ознаками: а) за характером досліджуваних об’єктів; б) за
- 181. За ступеня охоплення елементів сукупності індекси ділять на: а) індивідуальні; б) загальні; в) групові. Класифікація індексів
- 182. Класифікація індексів
- 183. Агрегатні індекси як вихідна форма індексів Агрегатним індексом в статистиці називається загальний індекс, який є відношенням
- 184. Агрегатні індекси як вихідна форма індексів індекс показує зміну кількості виробленої або реалізованої продукції в звітному
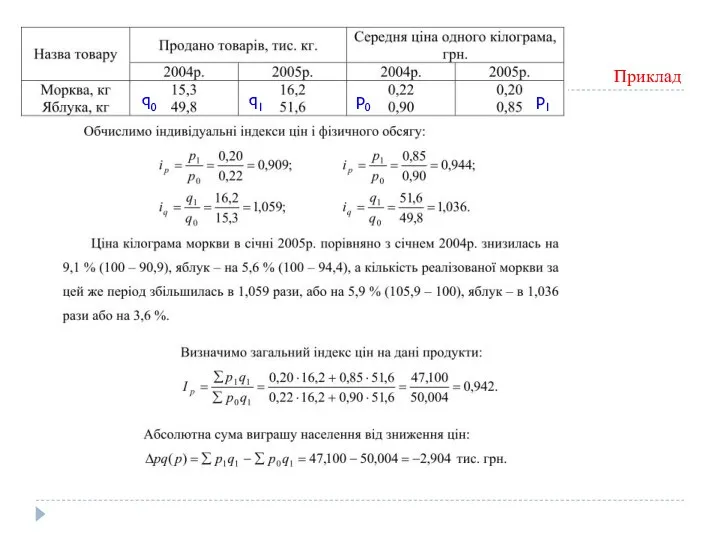
- 185. Приклад q1 q0 p1 p0
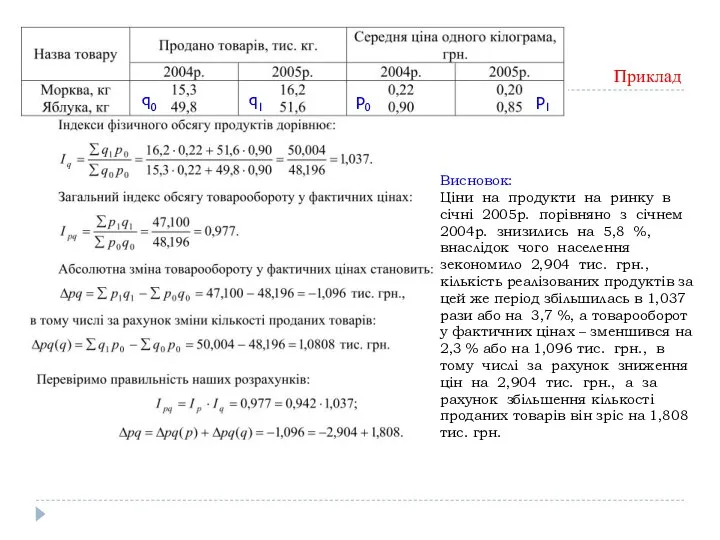
- 186. Приклад Висновок: Ціни на продукти на ринку в січні 2005р. порівняно з січнем 2004р. знизились на
- 187. Індекси із собівартості і кількості виготовленої продукції Індекси взаємозв’язані
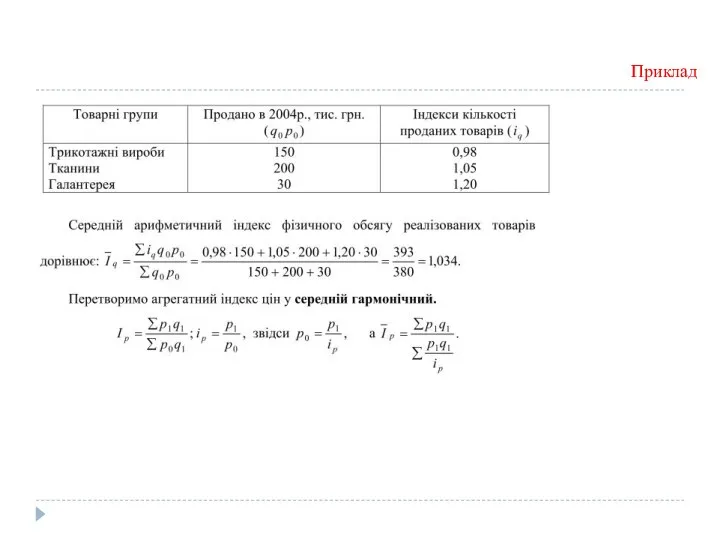
- 188. Середньозважені індекси
- 189. Приклад
- 190. Приклад
- 191. Базисні і ланцюгові індекси з постійними і змінними вагами
- 192. Базисні і ланцюгові індекси з постійними і змінними вагами
- 193. Базисні і ланцюгові індекси з постійними і змінними вагами
- 194. Індекси змінного, постійного складу і структурних зрушень
- 195. Індекси змінного, постійного складу і структурних зрушень
- 196. Приклад Дані про середню собівартість продукції «А» на двох заводах.
- 197. Приклад
- 198. Приклад
- 199. Територіальні індекси В практиці статистичних досліджень часто виникає потреба зпівставлення рівнів економічних явищ в просторі, для
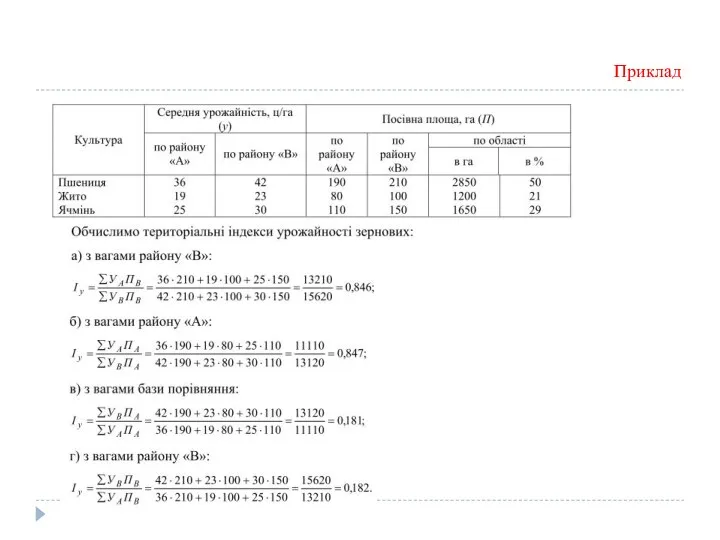
- 200. Приклад
- 201. Приклад
- 202. Приклад
- 203. Використання системи взаємозв’язаних індексів в аналізі чинників динаміки
- 204. Приклад
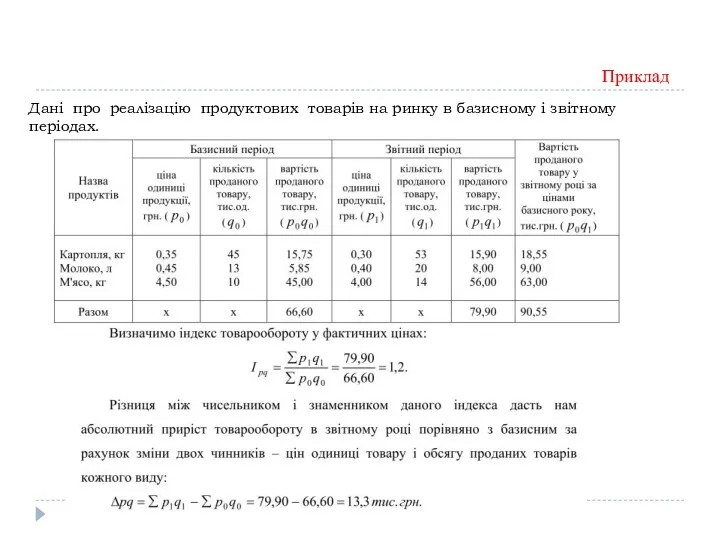
- 205. Дані про реалізацію продуктових товарів на ринку в базисному і звітному періодах. Приклад
- 206. Приклад
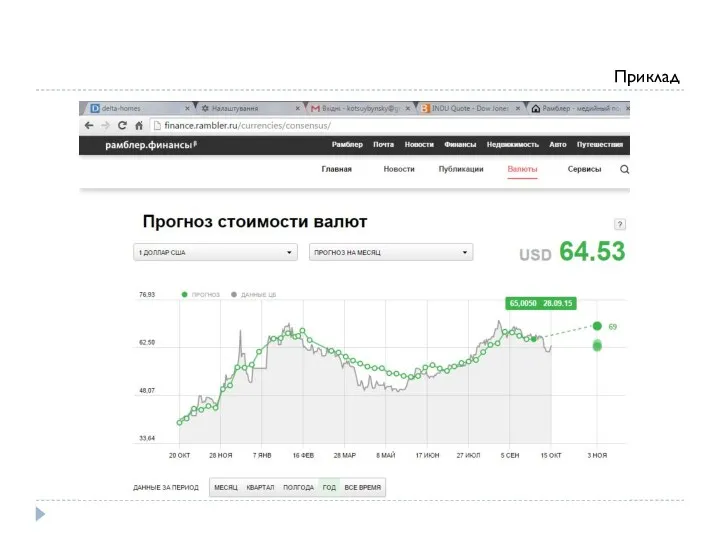
- 207. Фондовий індекс Фондовий індекс –комплексний показник на основі цін певної групи цінних паперів - «індексного кошика».
- 208. Зміни у величині акціонерного капіталу зумовлюють потребу в періодичному оцінюванні. Індекси акцій розраховують щодня. Зважування здійснюється
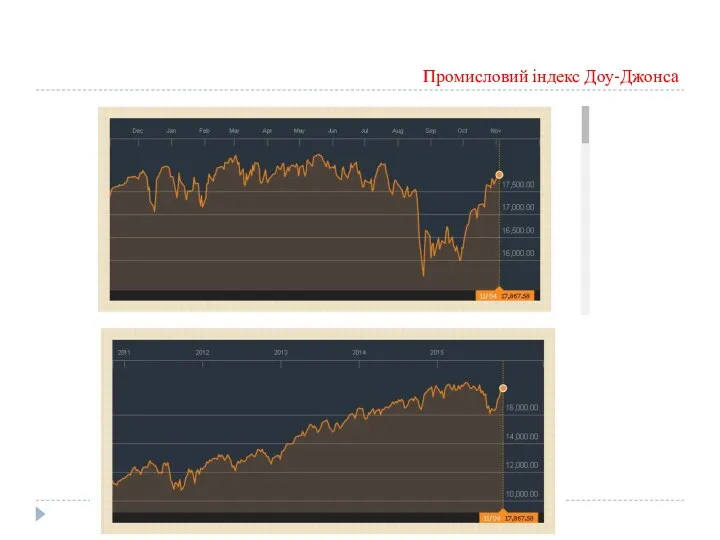
- 209. Промисловий індекс Доу-Джонса Промисловий індекс Доу-Джонса (Dow Jones Industrial, Dow 30, Dow Jones, The Dow) біржовий
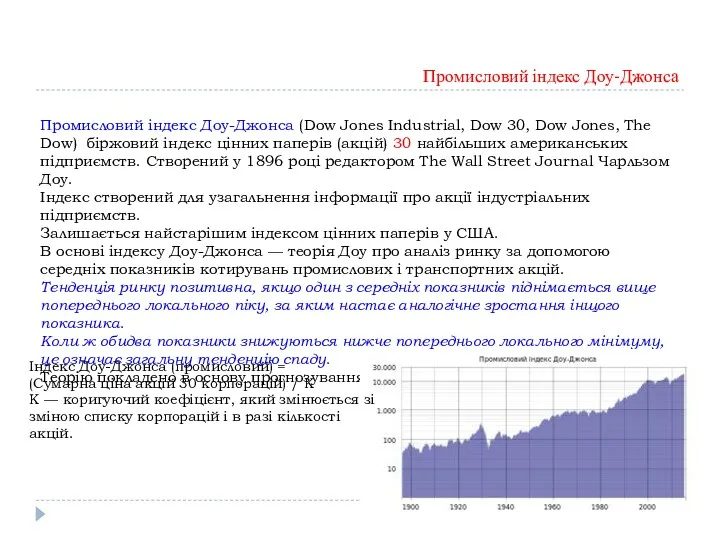
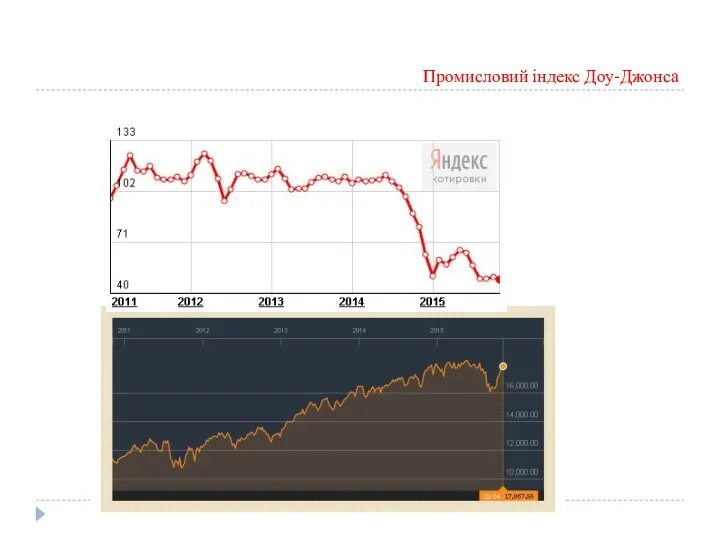
- 210. Промисловий індекс Доу-Джонса
- 211. Промисловий індекс Доу-Джонса
- 212. Індекс ПФТС —розраховується щодня за результатами торгів ПФТС на основі середньозваженої ціни за угодами. У «індексний
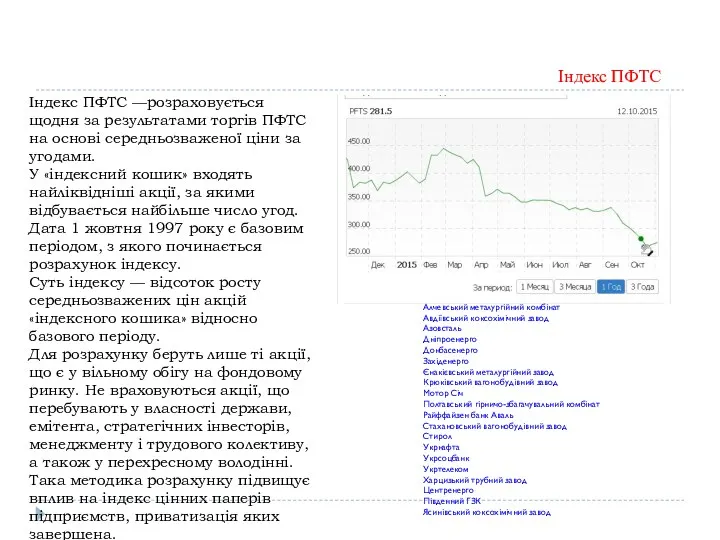
- 213. Лекція 8 Вибіркове спостереження Поняття про вибіркове спостереження та його основні завдання. Основні умови наукової організації
- 214. Поняття про вибіркове спостереження
- 215. Поняття про вибіркове спостереження
- 216. Основні завдання вибіркового спостереження
- 217. Основні методи формування вибірки При формуванні вибірки необхідно визначити: − хто (що) є елементом або одиницею
- 218. Основні умови наукової організації вибіркового спостереження Особливістю вибіркового спостереження в порівнянні з іншими видами несуцільного спостереження
- 219. При масовому спостереженні, розподіл емпіричних частот більшості явищ підпорядковується закону нормального розподілу. за нормальним розподілом більша
- 220. Методи і способи відбору одиниць у вибіркову сукупність Способом відбору називається система організації відбору одиниць з
- 221. На практиці статистичного дослідження використовуються три види відбору: 1) індивідуальний – відбір окремих одиниць сукупності; 2)
- 222. При типовому відборі генеральну сукупність поділяють на однорідні групи за певною ознакою, райони, зони. З кожної
- 223. Якщо необхідні дані можна отримати на основі вивчення всіх первинно відібраних одиниць, застосовують однофазну вибірку, а
- 224. Направлений відбір використовують тоді, коли за відомим середнім значенням ознаки в генеральній сукупності вибіркова сукупність повинна
- 225. Помилки репрезентативності Помилки репрезентативності становлять різницю між середніми і відносними показниками вибіркової сукупності та відповідними показниками
- 226. Формули для визначення середньої помилки репрезентативності випадкової і механічної вибірки для повторного і безповторного відбору. Знаходження
- 227. Знаходження граничної помилки для різних видів вибірок При вибірковому спостереженні розмір граничної помилки репрезентативності «∆» може
- 228. На основі формул граничної помилки вибірки розв’язують завдання: визначають довірчі межі генеральної середньої і частки з
- 229. Приклад При 2% випадковому відборі у відібраних для обстеження 100 деталей встановлено, що середня вага однієї
- 230. Приклад
- 231. Чисельність вибірки Чисельність вибірки залежить від наступних чинників: 1) від варіації досліджуваної ознаки - більша варіація
- 232. Для району, в якому є 8000 підприємців платників ПДВ , необхідно організувати вибіркове спостереження з метою
- 233. Способи поширення даних вибіркового спостереження на генеральну сукупність Кінцевою практичною метою вибіркового спостереження є поширення його
- 234. Лекція 9 Експертне оцінювання Обробка результатів експертного оцінювання Коефіцієнт конкордації Коефіцієнт компетенції .
- 235. Обробка результатів експертного оцінювання Важливим етапом у підведенні результатів дослідження є прогнозування, яке передбачає визначення значень
- 236. Коефіцієнт конкордації
- 237. Коефіцієнт конкордації
- 238. Приклад Група експертів з 3 осіб оцінювала час, що необхідний для виконання робіт певного проекту. Результати
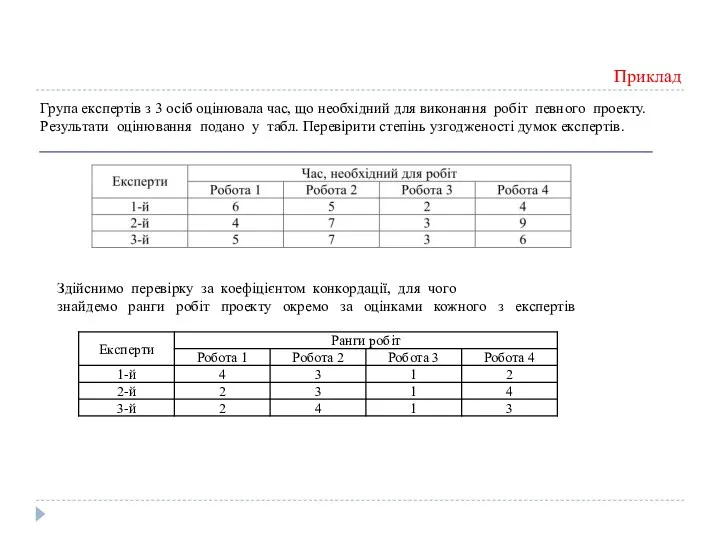
- 239. У групах рангів оцінок, наданих окремими експертами, немає однакових, тому коефіцієнт конкордації розраховуємо за формулою Приклад
- 240. Приклад Виокремимо експерта, оцінки якого є найбільш неузгодженими. Для цього побудуємо матрицю парних коефіцієнтів кореляції Пірсона
- 241. Розрахуємо коефіцієнт конкордації, враховуючи відсутність оцінок першого експерта. Приклад Значення коефіцієнта конкордації після виведення першого експерта
- 242. Коефіцієнт компетенції Використання коефіцієнта конкордації засновано на припущенні- чим більш узгоджені думки експертів, тим достовірнішими є
- 243. Коефіцієнт компетенції
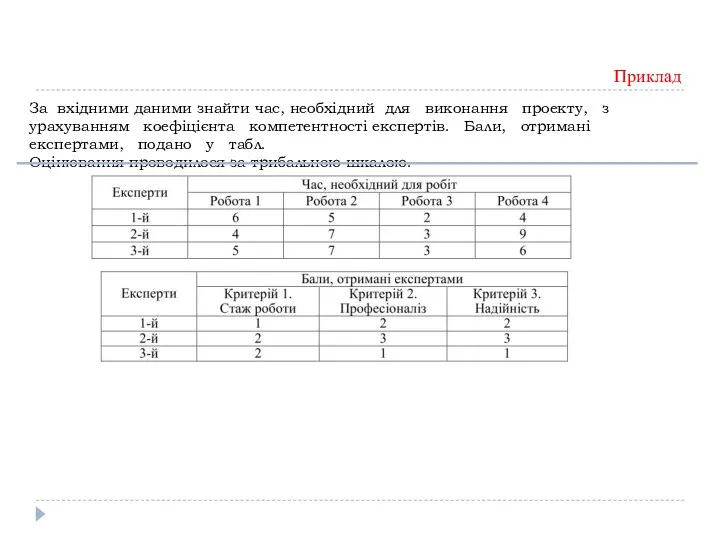
- 244. За вхідними даними знайти час, необхідний для виконання проекту, з урахуванням коефіцієнта компетентності експертів. Бали, отримані
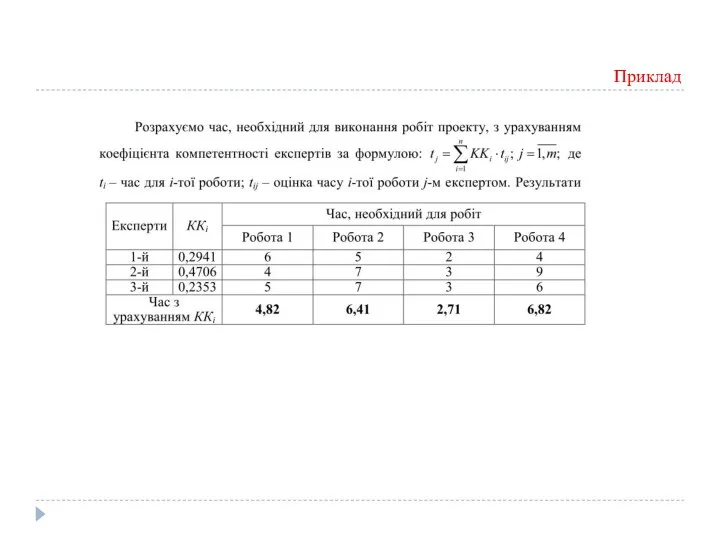
- 245. Знайдемо коефіцієнти компетентності експертів Приклад
- 246. Приклад
- 248. Скачать презентацию























































































































































































 Принципы работы протоколов разных уровней. . Стеки OSI, TCP/IP, IPX/SPX, NetBIOS/SMB. (Тема 11)
Принципы работы протоколов разных уровней. . Стеки OSI, TCP/IP, IPX/SPX, NetBIOS/SMB. (Тема 11) Текстовый редактор Word
Текстовый редактор Word SQL. База данных
SQL. База данных Двоичная система счисления
Двоичная система счисления Процедуры и функции. Программирование на языке Python
Процедуры и функции. Программирование на языке Python Программа Microsoft PowerPoint
Программа Microsoft PowerPoint Алгоритм
Алгоритм Основные алгоритмические конструкции
Основные алгоритмические конструкции Информационное общество
Информационное общество 9-2-4
9-2-4 Google Forms
Google Forms Персональный компьютер
Персональный компьютер Математическая логика. 9 класс
Математическая логика. 9 класс Графический редактор
Графический редактор Вёрстка сайтов HTML & CSS
Вёрстка сайтов HTML & CSS Разработка информационной системы учёта почтовых отправлений в отделении Почты России
Разработка информационной системы учёта почтовых отправлений в отделении Почты России Технология разработки программного обеспечения
Технология разработки программного обеспечения Управление проектами, международная практика. Этапы Внедрения Спайдер Проджект
Управление проектами, международная практика. Этапы Внедрения Спайдер Проджект Памятка по установке ОТП кредит
Памятка по установке ОТП кредит Инновационная образовательная программа
Инновационная образовательная программа Скоростное прохождение игр
Скоростное прохождение игр Цифровой звук (8 класс)
Цифровой звук (8 класс) 5. Распределение памяти
5. Распределение памяти Шағын кәсіпорын мысалында iт-технологияларды қолданудың
Шағын кәсіпорын мысалында iт-технологияларды қолданудың Система электронных дневников и журналов
Система электронных дневников и журналов Библиотека будущего
Библиотека будущего HTML язык презентация
HTML язык презентация Информационные ресурсы интернета
Информационные ресурсы интернета