Простые числа презентация

Простые числа важны не только в математике. Многие даже не догадываются, что они играют важную роль в нашей повседневной жизни, например, в банковских операциях или в обеспечении защиты персональных компьютеров и конфиденциальности разговоров по мобильному телефону. Они являются краеугольным камнем компьютерной безопасности.
Электронная почта, банковские операции, кредитные карты и мобильная телефонная связь – все это защищено секретными кодами, непосредственно основанными на свойствах простых чисел.
Возникает проблема: как проверить большое число на простоту, чтобы использовать его для шифрования?

Объектом изучения являются простые числа.
Цель работы: изучение алгоритмов для проверки чисел на простоту.
Задачи:
Изучить методы нахождения простых чисел;
Рассмотреть алгоритмы для проверки чисел на простоту.
Рассмотреть реализацию теста Ферма на языке программирования Pascal.

Простое число - это натуральное число, которое имеет только два делителя (единицу и само это число).
Примеры: 3 – делители 3 и 1; 5 – делители 5 и 1.

Древнегреческий математик Эратосфен, живший более чем за 200 лет до н.э., составил первую таблицу простых чисел, которая получила название «Решето Эратосфена».
Название «решето» метод получил потому, что, согласно легенде, Эратосфен писал числа на дощечке, покрытой воском, и прокалывал дырочки в тех местах, где были написаны составные числа. Поэтому дощечка являлась неким подобием решета, через которое «просеивались» все составные числа, а оставались только числа простые. Эратосфен дал таблицу простых чисел до 1000.

Алгоритм нахождения простых чисел
(решето Эратосфена)
Выпишем несколько подряд идущих чисел, начиная с 2. Двойку отберём в свою коллекцию, а остальные числа, кратные 2, зачеркнем. Ближайшим не зачёркнутым числом будет 3. Возьмём в коллекцию и его, а все остальные числа, кратные 3, зачеркнем). При этом окажется, что некоторые числа уже были вычеркнуты раньше, как, например, 6, 12 и др. Следующее наименьшее не зачёркнутое число – это 5. Берем пятерку, а остальные числа, кратные 5,зачеркиваем. Теперь берем семерку, а остальные числа, кратные.
Повторяя эту процедуру снова и снова, добьемся того, что не зачеркнутыми останутся одни лишь простые числа (на рисунке они обведены в кружок).

Простыми числами занимался и древнегреческий математик Евклид (IIIв. до н.э.).
Евклид - древнегреческий математик, автор первого из дошедших до нас теоретических трактатов по математике. Евклид доказал, что простых чисел бесконечно много. Можно сказать также, что среди простых чисел нет самого большого числа. Много ученых пытались найти общую формулу для записи простых чисел, но все их попытки не увенчались успехом.

Доказательство теоремы Евклида может быт кратко воспроизведено так:
Представим, что количество простых чисел конечно. Перемножим их и прибавим единицу. Полученное число не делится ни на одно из конечного набора простых чисел, потому что остаток от деления на любое из них даёт единицу. Значит, число должно делиться на некоторое простое число, не включённое в этот набор. Получили противоречие. Таким образов, простых чисел бесконечно много.

На практике вместо получения списка простых чисел зачастую требуется проверить, является ли данное число простым.
Например, для шифрования используются большие простые числа и возникает необходимость проверки числа на простоту.

Алгоритмы, решающие эту задачу, называются тестами простоты.
Существуют универсальные и специализированные тесты простоты. Универсальные тесты используются для любых чисел. Специализированные тесты применяются для определенного класса чисел.
Например,
тест Люка – Лемера для чисел Мерсена.

Различают также полиномиальные, детерминированные и вероятностные тесты простоты.
Полиномиальность означает, что наибольшее время работы алгоритма ограничено многочленом от количества цифр в проверяемом числе.
Детерминизм гарантирует получение уникального предопределённого результата.
Вероятностные тесты могут проверить простоту числа за полиномиальное время, но при этом дают лишь вероятностный ответ.

Тест Ферма
Тест простоты Ферма — это тест простоты натурального числа n, основанный на малой теореме Ферма.
Малая теорема Ферма: если р – простое число и а – целое число, не делящееся на р, то aр-1 – 1 делится на р без остатка, т.е. aр-1≡1(mod р).

Алгоритм теста Ферма
Тест Ферма на простоту числа n по основанию a:
Если для основания a и модуля n выполняется an-1≡1(mod n), то n может быть простым числом.
Если an-1≡1(mod n), то n - однозначно составное.

При проверке числа на простоту тестом Ферма выбирают несколько чисел a. Чем больше количество a, для которых an-1≡1(mod n), тем больше шансы, что число n простое. Однако существуют составные числа, для которых сравнение an-1≡1(mod n) выполняется для всех a, взаимно простых с n — это числа Кармайкла. Чисел Кармайкла — бесконечное множество, наименьшее число Кармайкла — 561. Тем не менее, тест Ферма довольно эффективен для обнаружения составных чисел.
Число Кармайкла составное число n, такое что an-1≡1(mod n), для всех целых чисел a, взаимно простых с n (561, 1105, 1729, 2465, 2821, 6601, 8911, 10585, 15841, 29341, 41041, 46657, 52633, 62745, 63973, 75361, …).

Пример.
Проведите испытание Ферма для числа n = 5.
Решение.
Возьмем а = 2.
25 – 1= 1 (mod 5) →( 25– 1- 1) :5 = 3 (без остатка). Получаем, число 5 – может быть простым.
Возьмем а = 3.
35 – 1= 1 (mod 5) →( 35– 1- 1) :5 = 16 (без остатка). Получаем, число 5 – может быть простым.
Таким образом, 5 – простое число.

Тест Миллера – Рабина
Тест Миллера — Рабина — вероятностный полиномиальный тест простоты. Тест Миллера — Рабина позволяет эффективно определять, является ли данное число составным. Однако, с его помощью нельзя строго доказать простоту числа. Тем не менее тест Миллера — Рабина часто используется в криптографии для получения больших случайных простых чисел.
Алгоритм был разработан Гари Миллером в 1967 году и модифицирован Майклом Рабином в 1980 году.

Тест Соловея – Штрассена
Тест Соловея — Штрассена - вероятностный тест простоты, открытый в 1970-х годах Робертом Мартином Соловеем совместно с Фолькером Штрассеном. Тест всегда корректно определяет, что простое число является простым, но для составных чисел с некоторой вероятностью он может дать неверный ответ.

Алгоритм Соловея – Штрассена
Сначала для алгоритма выбирается целое число k ≥ 1. Тест проверки простоты числа n состоит из k отдельных раундов. В каждом раунде выполняются следующие действия:
Случайным образом выбирается число a < n, и вычисляется d = НОД (a,n).
Если d > 1, то выносится решение о том, что n – составное. Иначе проверяется сравнение (*). Если оно не выполнено, то n – составное. Иначе, a является свидетелем простоты числа n.
Если после завершения k раундов найдено k свидетелей простоты, то делаем заключение «n – вероятно просто число».

Тест Люка – Лемера
Тест был предложен французским математиком Люка в 1878 году и дополнен американским математиком Лемером в 1930 году. Полученный тест носит имя двух ученых, которые совместно открыли его, даже не встречаясь при жизни.
Тест Люка — Лемера — эффективный тест простоты для чисел Мерсена. Благодаря этому тесту самыми большими известными простыми числами всегда были простые числа Мерсена, причём даже до появления компьютеров.

Тест Адлемана – Померанса – Румели
В начале 80-х годов Адлеман, Померанc и Румели предложили детерминированный алгоритм проверки простоты чисел. Для заданного натурального числа n алгоритм выдает верный ответ, составное n или простое.
Этот алгоритм оказался непрактичным и довольно сложным для реализации на компьютере.
Существенные теоретические упрощения алгоритма Адлемана— Померанса—Румели были получены X. Ленстрой.
Реализация этого алгоритма позволила проверять на простоту числа n порядка 10100 за несколько минут.

Алгоритм Ленстры – Коена
Дальнейшие усовершенствования алгоритма Адлемана— Померанса—Румели и алгоритма Ленстры были предложены Ленстрой и Коеном.
Однако на практике он ока­зался наиболее эффективным. При правильной организации его работы алгоритм всегда достаточно быстро выдает правильный ответ, простое n или составное. Описание и теоретическое обоснование алгоритма Ленстра—Коена довольно-таки объемно. Этот алгоритм проверяет на простоту числа порядка 10100 - 10200 за несколько минут

Тест Агравала – Каяла – Саксены
В 2004 г. индийскими учеными Маниндрой Агравалом и его двумя студентами Нираджем Каялом и Нитином Саксеной Индийского технического института Канпура был разработан полиномиальный детерминированный тест простоты. За свое открытие авторы получили премию Гёделя и приз Фалькерсона в 2006 году.

Тест Аграва́ла — Кая́ла — Саксе́ны (тест AKS) — единственный известный на данный момент универсальный (то есть применимый ко всем числам) полиномиальный, детерминированный и безусловный (то есть не зависящий от недоказанных гипотез) тест простоты чисел, основанный на обобщении малой теоремы Ферма на многочлены.

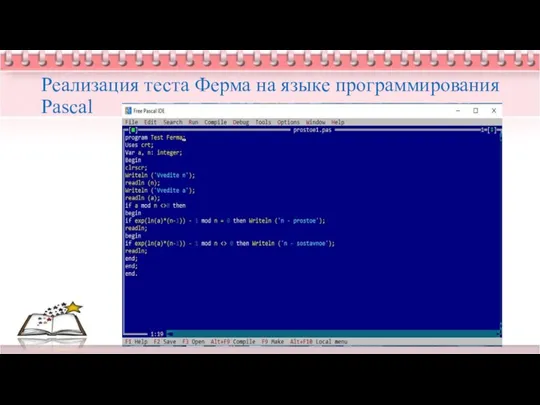
Реализация теста Ферма на языке программирования Pascal

Вывод
Многие ученые на протяжении многих веков вносили свой вклад в изучение темы «Простые числа». В настоящее время исследование простых чисел и алгоритмы проверки их на простоту продолжаются, ученые делают и будут делать новые открытия!
В работе «Простые числа» я изучил методы нахождения простых чисел, рассмотрел тесты простоты и реализовал тест Ферма на языке программирования Pascal. Узнал, что указать самое большое простое число невозможно, т.к. они бесконечны.
Казалось бы, простые числа – чего уж может быть проще. А, оказывается, можно сделать еще столько открытий, и столько проблем ждут своего доказательства.