Содержание
- 2. Задача 1. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Каково наибольшее целое число X, при котором истинно
- 3. Задача 2. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Укажите значения переменных K, L, M, N, при
- 4. Задача 3. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Сколько различных решений имеет уравнение (X ∧ Y
- 5. Задача 4. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Сколько различных решений имеет уравнение J ∧ ¬K
- 6. Задача 5. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Сколько существует различных наборов значений логических переменных x1,
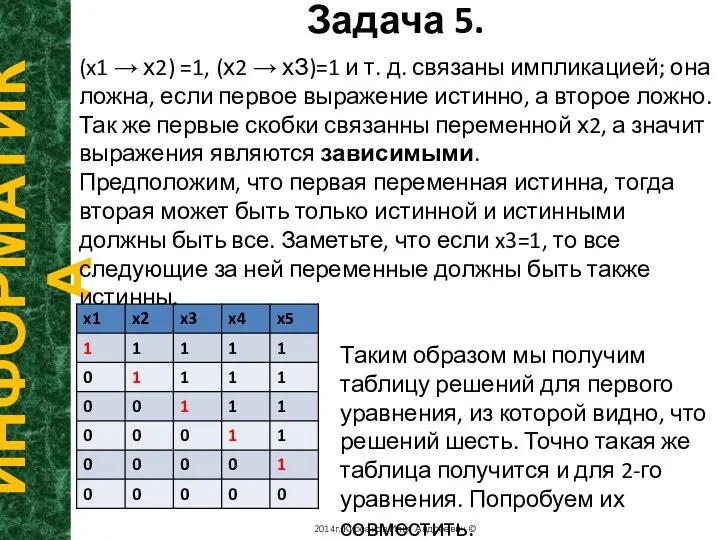
- 7. Задача 5. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © (x1 → х2) =1, (х2 → хЗ)=1 и
- 8. Задача 5. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Рассмотрим условие: x1 ∨ y1 = 1, исключим
- 9. Задача 5. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Всего у нас 6*6 = 36 решений в
- 10. Задача 6. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Сколько существует различных наборов значений логических переменных x1,x2,x3,x4,x5,x6,x7,x8,
- 11. Задача 6. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Далее нам следует заменить выражения в скобках буквенными
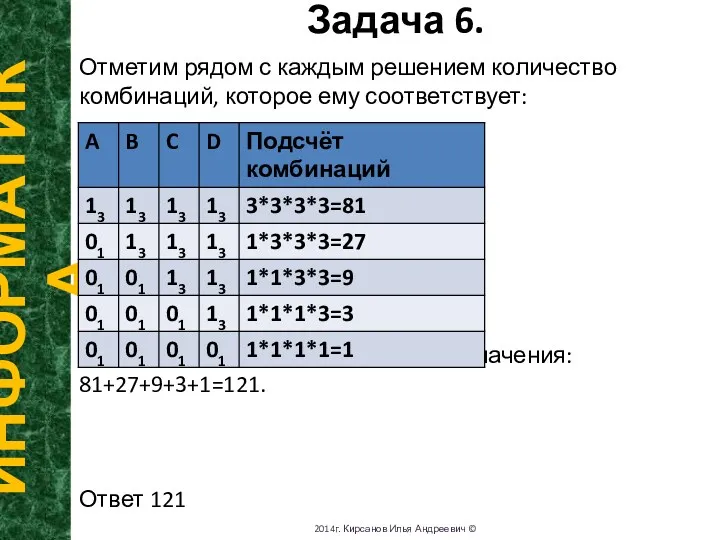
- 12. Задача 6. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Отметим рядом с каждым решением количество комбинаций, которое
- 13. Задача 7. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Сколько существует различных наборов значений логических переменных x1,
- 14. Задача 7. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © (x1≡x2)→(x3≡x4)=1 (x3≡x4)→(x5≡x6)=1 (x5≡x6)→(x7≡x8)=1 (x7≡x8)→(x9≡x10)=1 Сделаем, как в предыдущей
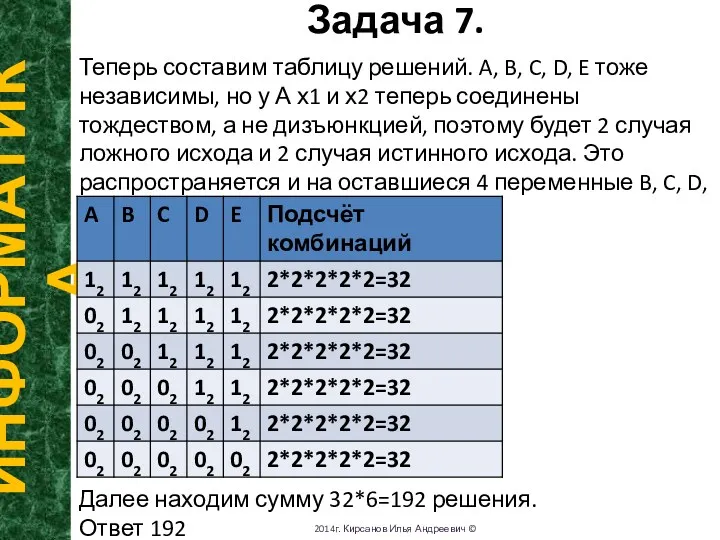
- 15. Задача 7. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Теперь составим таблицу решений. A, B, C, D,
- 16. Задача 8. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Сколько существует различных наборов значений логических переменных x1,
- 17. Задача 8. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Вначале преобразуем: (x1 ∧ x2) ∨ (¬x1 ∧
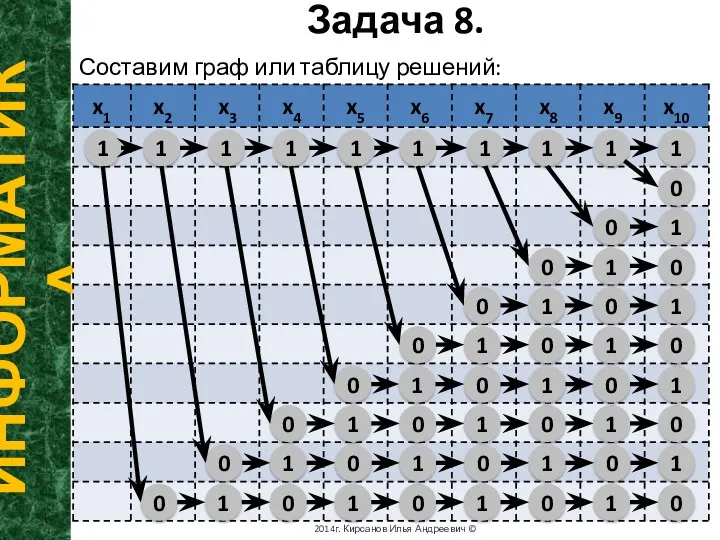
- 18. Задача 8. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Составим граф или таблицу решений: 1 1 1
- 19. Задача 8. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Из таблицы видно, что существует 10 решений для
- 20. Вопросы. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Сколько существует различных наборов значений логических переменных x1, x2,
- 21. Вопросы. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Сколько различных решений имеет система уравнений ¬x1 ∨ x2
- 22. Вопросы. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Сколько существует различных наборов значений логических переменных x1, x2,
- 24. Скачать презентацию

















 Элективное занятие по информатике в 9 классе
Элективное занятие по информатике в 9 классе О браузерах в интернете
О браузерах в интернете SimCorp APL
SimCorp APL Социальная сеть, как основа современной культуры
Социальная сеть, как основа современной культуры Типология современных радиостанций
Типология современных радиостанций Об'єктно-орієнтований аналіз
Об'єктно-орієнтований аналіз Формулы в электронных таблицах. Тест
Формулы в электронных таблицах. Тест RAM, ROM and Virtual memory
RAM, ROM and Virtual memory Четыре основных типа запросов данных в SQL
Четыре основных типа запросов данных в SQL Тема: Базы данных
Тема: Базы данных Сведения о языке программирования Паскаль
Сведения о языке программирования Паскаль Курс по основам программирования на Python. Функции
Курс по основам программирования на Python. Функции Фриланс, как форма занятности
Фриланс, как форма занятности Представление графической информации. Виды графики
Представление графической информации. Виды графики Защита информации в базах данных
Защита информации в базах данных Виды профессиональной информационной деятельности человека с использованием технических средств и информационных ресурсов
Виды профессиональной информационной деятельности человека с использованием технических средств и информационных ресурсов Техзадание к сайту
Техзадание к сайту Формализация понятия алгоритма
Формализация понятия алгоритма Компьютерная графика. Борьба с шумом изображений. (Лекция 5)
Компьютерная графика. Борьба с шумом изображений. (Лекция 5) Безопасный интернет
Безопасный интернет Браузер. Кем и когда создан
Браузер. Кем и когда создан Етапи побудови інформаційної моделі. Побудова інформаційних моделей. 7 клас
Етапи побудови інформаційної моделі. Побудова інформаційних моделей. 7 клас Deployment techniques for LabVIEW™ Applications
Deployment techniques for LabVIEW™ Applications The Great Alone Audiobook for Free Download
The Great Alone Audiobook for Free Download Разработка программного средства Портфолио студента
Разработка программного средства Портфолио студента Презентация Основы работы в векторном редакторе Corel Draw 11. Графические эффекты.
Презентация Основы работы в векторном редакторе Corel Draw 11. Графические эффекты. Introduction to spring framework and dependency injection
Introduction to spring framework and dependency injection Безопасность в Интернете
Безопасность в Интернете