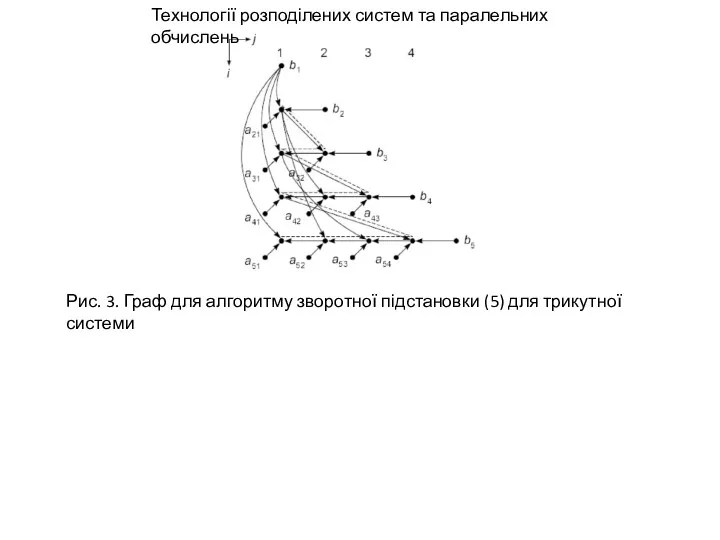
Отриманий результат є досить несподіваним. Обидва алгоритми (4) та (5) призначені
для розв’язування тієї самої задачі і розроблені на основі формул (3). Обидва алгоритми абсолютно однакові з точки зору їх реалізації на багатопроцесорній системі, оскільки потребують виконання однакової кількості операцій множення та віднімання і однакового об’єму пам’яті і є еквівалентними з точки зору помилок заокруглення.
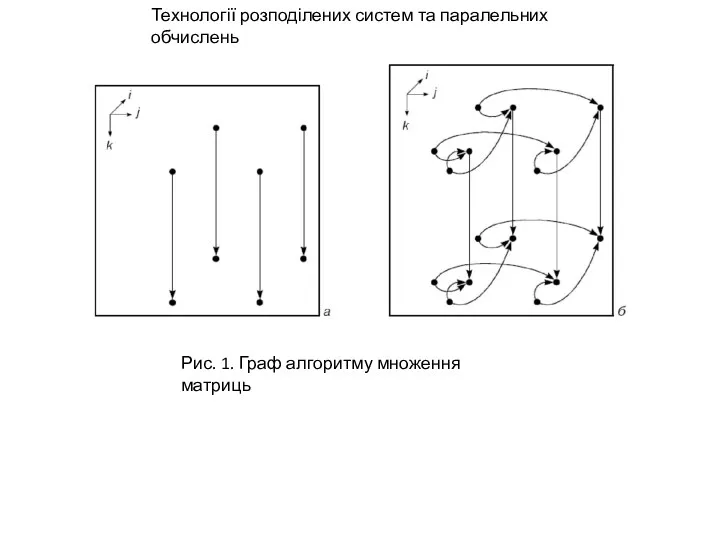
Тим не менш, паралельні графи алгоритмів принципово різні. Якщо ці алгоритми реалізувати на паралельній системі з n універсальними процесорами, то алгоритм (4) можна реалізувати за час, пропорційний n, а алгоритм (5) — лише за час пропорційний . У першому випадку завантаженість процесорів близька до 0, 5, а у другому — до 0.
Таким чином, алгоритми, цілком однакові при послідовній реалізації, можуть виявитися принципові відмінними при реалізацій на паралельній обчислювальній системі.
В цьому, взагалі кажучи, і полягає основна складність програмування програмного забезпечення для обчислень на паралельних комп’ютерах.
Технології розподілених систем та паралельних обчислень











 Компьютерная графика. Введение. Основные понятия и возможности компьютерной графики
Компьютерная графика. Введение. Основные понятия и возможности компьютерной графики Formularze w HTML5
Formularze w HTML5 Кадровые ресурсы информационных технологий. (Лекция 7)
Кадровые ресурсы информационных технологий. (Лекция 7) Точка отсчета. Интернет-игра нового поколения
Точка отсчета. Интернет-игра нового поколения Формування багатотабличного SQL-запиту
Формування багатотабличного SQL-запиту Компьютерные изображения
Компьютерные изображения Автоматизоване створення та публікування веб-сайтів
Автоматизоване створення та публікування веб-сайтів Механизм расширения языка
Механизм расширения языка Види підключення до Internet
Види підключення до Internet Объектно-ориентированное программирование. Базовые и утилитные классы API JAVA
Объектно-ориентированное программирование. Базовые и утилитные классы API JAVA Графические информационные модели
Графические информационные модели Системный анализ
Системный анализ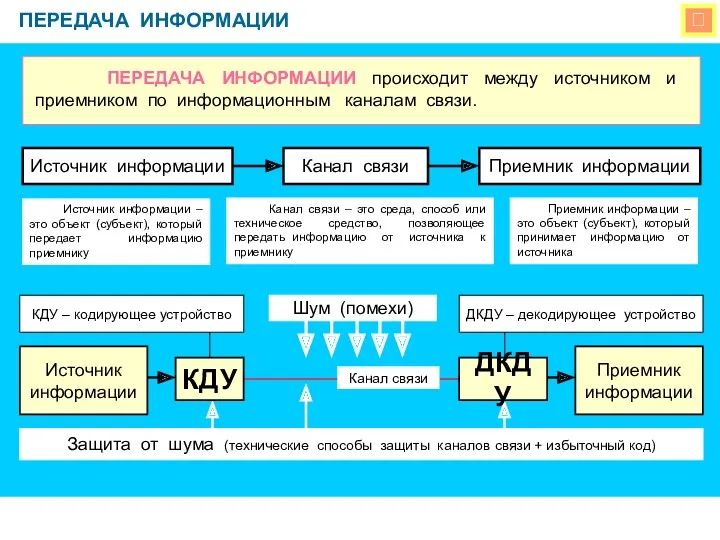 Передача информации.
Передача информации. Поняття інформації. Повідомлення
Поняття інформації. Повідомлення Инструкция по покупке электронных билетов на сайте ОАО РЖД с использованием виртуальных транспортных требований
Инструкция по покупке электронных билетов на сайте ОАО РЖД с использованием виртуальных транспортных требований Компьютерные вирусы и антивирусные программы
Компьютерные вирусы и антивирусные программы Қоғам дамуының шешуші секторларында АКТ-дың рөлі.АКТ-дың стандарттары
Қоғам дамуының шешуші секторларында АКТ-дың рөлі.АКТ-дың стандарттары Спілкування як обмін інформацією
Спілкування як обмін інформацією Программирование на Паскале - первый уровень. Простые (линейные) программы
Программирование на Паскале - первый уровень. Простые (линейные) программы Ребенок и компьютер
Ребенок и компьютер Информационные технологии, применяемые в правоохранительной деятельности
Информационные технологии, применяемые в правоохранительной деятельности Steam. About Steam. History. User Interface. Games
Steam. About Steam. History. User Interface. Games Бизнес – информатика и специалисты будущего Акулы бизнеса
Бизнес – информатика и специалисты будущего Акулы бизнеса Wireshark
Wireshark Электронный бизнес и его место в современной экономике
Электронный бизнес и его место в современной экономике Информация, ее виды и свойства
Информация, ее виды и свойства Презентация программы по информатике.
Презентация программы по информатике. Особливості використання класів
Особливості використання класів