где n ⎯ число диагоналей, предшествующих основанию. Ясно, что n есть
целый неотрицательный корень уравнения
Решение (Лучшее объяснение): Пусть имеется некоторое k, занимающее в
сетке позицию (i , j), N — число элементов внутри с основанием, концы
которого имеют координаты (i, 1) и (1, i):
Задача № 1.1.
или
Уравнение (1) имеет целые неотрицательные
корни только при N, расположенных в строчке 1.
Надо вычислять последовательно Nm = 1 + 2 + … + m (m = 1, 2, …) до тех пор, пока при некотором m не окажется, либо
а) Nm = k, либо б) Nm − 1 < k < Nm .
В случае а) решить ур. (1) при N = Nm и положить i = 1, j = n .
В случае б) j = k – Nm − 1 ; и учитывая, что i + j = n + 2 , где n корень уравнения (1) при N = Nm − 1 , получим i = n + 2 – j .
Как узнать, число k ⎯ в 1-й строчке или нет?















 Автоматизированная система организации спортивных мероприятий
Автоматизированная система организации спортивных мероприятий Увлекательный киберспорт, или какие игры лучше для трансляций
Увлекательный киберспорт, или какие игры лучше для трансляций Причины и типы ошибок
Причины и типы ошибок Информационные ресурсы современного общества
Информационные ресурсы современного общества Методика обеспечения строительного контроля с использованием информационной модели здания
Методика обеспечения строительного контроля с использованием информационной модели здания Файлы и файловая система
Файлы и файловая система Устройство компьютера. Носители информации ( 5 класс)
Устройство компьютера. Носители информации ( 5 класс) Применение динамических массивов в структурном подходе
Применение динамических массивов в структурном подходе Методическая разработка урока по теме Компьютерные вирусы. Антивирусные программы
Методическая разработка урока по теме Компьютерные вирусы. Антивирусные программы Сетевая этика. Культура общения в сети
Сетевая этика. Культура общения в сети Верификация программного обеспечения. Дефекты
Верификация программного обеспечения. Дефекты WEB-программирование, семинар 5
WEB-программирование, семинар 5 Новые пакеты услуг Кибернетики
Новые пакеты услуг Кибернетики Работа в ПО Sieble
Работа в ПО Sieble Графические редакторы MediaBang Paint Pro и Artwaver Free
Графические редакторы MediaBang Paint Pro и Artwaver Free База данных как модель предметной области
База данных как модель предметной области Повышение эффективности работы баз данных. Обработка транзакций OLTP-OLAP системы мониторы транзакций
Повышение эффективности работы баз данных. Обработка транзакций OLTP-OLAP системы мониторы транзакций Парсинг HTML. Краткий обзор технологий для понимания сбора и обработки данных
Парсинг HTML. Краткий обзор технологий для понимания сбора и обработки данных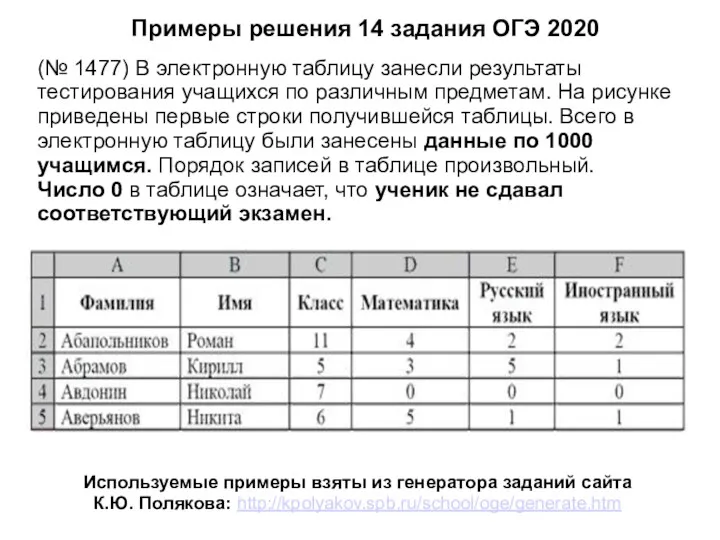 Примеры решения задания 14, ОГЭ по информатике
Примеры решения задания 14, ОГЭ по информатике Программы для видеоконференций. Введение
Программы для видеоконференций. Введение Онлайн-сервисы для создания электронных игр и викторин
Онлайн-сервисы для создания электронных игр и викторин Автоматизация научных исследований
Автоматизация научных исследований Цвет. Background. Градиент
Цвет. Background. Градиент Методическая разработка внеклассного мероприятия (интеллектуальная игра) по физике и информатике для учащихся 5-11 классов Кто хочет стать отличником
Методическая разработка внеклассного мероприятия (интеллектуальная игра) по физике и информатике для учащихся 5-11 классов Кто хочет стать отличником Операционная система
Операционная система Нові можливості функцій в мові С++
Нові можливості функцій в мові С++ Переход от инфологического моделирования к моделям данных и знаний. Логико-лингвистические модели представления знаний
Переход от инфологического моделирования к моделям данных и знаний. Логико-лингвистические модели представления знаний КВН по информатике
КВН по информатике