Содержание
- 2. Виды орнаментов: По характеру композиции и расположению на украшаемой поверхности орнамент может быть нескольких видов.
- 3. Ленточный или бордюр
- 4. Сетчатый
- 5. Розеточный
- 6. При исследовании строения кристаллов выяснилось, что их атомы расположены очень правильным образом, образуя как бы геометрический
- 7. В математике паркетом называется разбиение плоскости на многоугольники, при котором каждые два многоугольника либо не пересекаются,
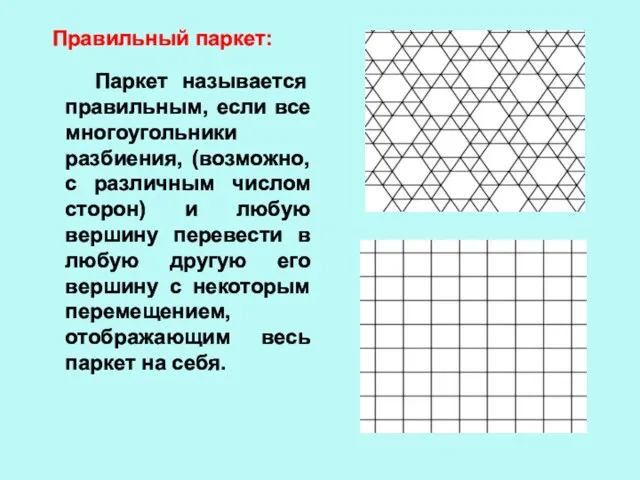
- 8. Правильный паркет: Паркет называется правильным, если все многоугольники разбиения, (возможно, с различным числом сторон) и любую
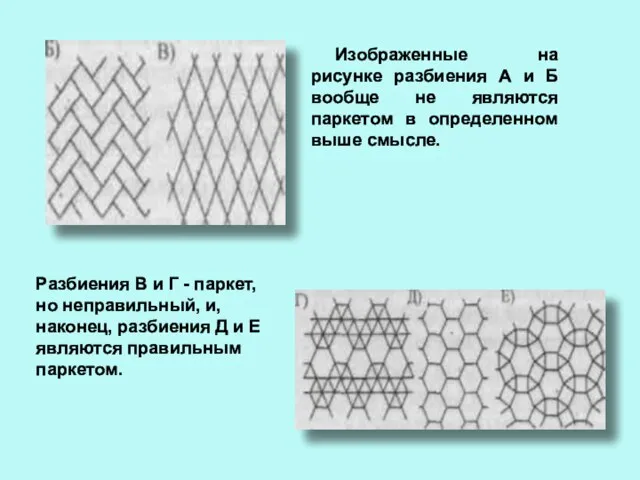
- 9. Изображенные на рисунке разбиения А и Б вообще не являются паркетом в определенном выше смысле. Разбиения
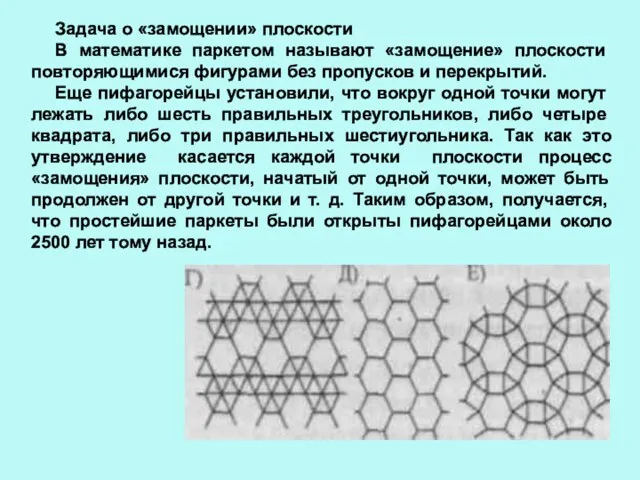
- 10. Задача о «замощении» плоскости В математике паркетом называют «замощение» плоскости повторяющимися фигурами без пропусков и перекрытий.
- 11. Более сложный паркет-орнамент можно сконструировать, если построить на сторонах квадрата правильные треугольники, а на сторонах этих
- 12. Мозаика поливных плиток на сооружениях мемориального ансамбля Шах-и-Зинда в Самарканде дает пример построения орнаментов, в которых
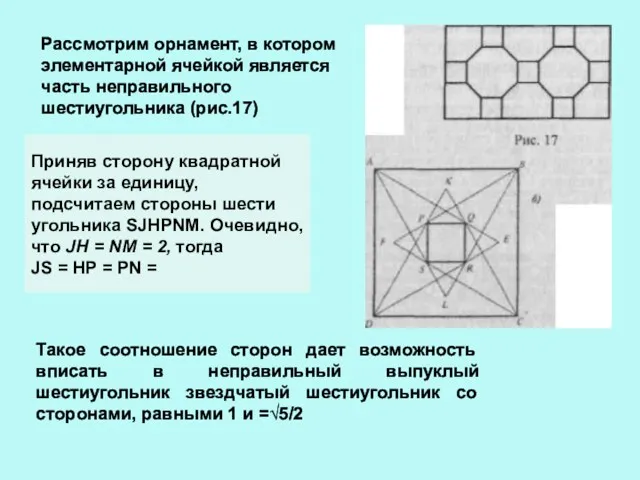
- 13. Рассмотрим орнамент, в котором элементарной ячейкой является часть неправильного шестиугольника (рис.17) Приняв сторону квадратной ячейки за
- 14. Вывод: Решение задач, связанных с архитектурными орнаментами, убеждает в том, что геометрия занимала важное место в
- 16. Скачать презентацию









 Постимпрессионизм в живописи
Постимпрессионизм в живописи Русский народный женский костюм
Русский народный женский костюм Медиасистема Японии
Медиасистема Японии Убранство русской избы. 5 класс
Убранство русской избы. 5 класс Русское узорочье
Русское узорочье Архитектура России в XVII веке
Архитектура России в XVII веке Правила построения комиксов. Раскадровка
Правила построения комиксов. Раскадровка Основные принципы ландшафтного дизайна
Основные принципы ландшафтного дизайна Происхождение аниме
Происхождение аниме Etyka w administracji publicznej
Etyka w administracji publicznej Витраж. Роспись по стеклу
Витраж. Роспись по стеклу Импрессионизм в музыке и живописи
Импрессионизм в музыке и живописи Традиции народа Африки. Бушмены
Традиции народа Африки. Бушмены Оригами. Бумажная лошадка
Оригами. Бумажная лошадка Архитектурные ансамбли Петербурга
Архитектурные ансамбли Петербурга Стиль Шебби-Шик в интерьере
Стиль Шебби-Шик в интерьере Локшина и галушки
Локшина и галушки Танцы народов мира. Тест
Танцы народов мира. Тест Прекрасное и безобразное в дизайне
Прекрасное и безобразное в дизайне Ритм пятен, как средство выражения
Ритм пятен, как средство выражения Все народы воспевают мудрость старости
Все народы воспевают мудрость старости Испанская картина мира сквозь призму национальной живописи
Испанская картина мира сквозь призму национальной живописи Новогодние традиции разных стран мира
Новогодние традиции разных стран мира Экскурсиятануға кіріспе. ХVIII-ХІХ Ғ.Ғ. экскурсиялық істің пайда болуы
Экскурсиятануға кіріспе. ХVIII-ХІХ Ғ.Ғ. экскурсиялық істің пайда болуы Глоссарий архитектурных терминов с картинками
Глоссарий архитектурных терминов с картинками What is a graphic novel
What is a graphic novel Қазақтың ұлттық ою-өрнектері
Қазақтың ұлттық ою-өрнектері Проектная деятельность на уроках изобразительного искусства
Проектная деятельность на уроках изобразительного искусства