Содержание
- 2. مؤلف: ليدا فرخي تهيه ي پاور پوينت: اردوان ميرزايي تعداد واحد : 3
- 3. اهداف درس توانايي حل مسئله تقويت تفكر رياضي آشنايي با: بردارها ماتريس و دترمينان دستگاه معادلات
- 4. فهرست مطالب فصل اول: بردارها فصل دوم:ماتريس و دترمينان فصل سوم: دستگاه معادلات خطي و توابع
- 5. فصل اول: بردارها بردارها در صفحه ضرب عددي دو بردار بردارها در فضاي سه بعدي ضرب
- 6. فصل دوم:ماتريس و دترمينان ماتريس دترمينان وارون ماتريس
- 7. فصل سوم: دستگاه معادلات خطي و توابع خطي دستگاه معادلات استقلال و وابستگي خطي رتبه ي
- 8. فصل چهارم: توابع چند متغيره توابع چند متغيره حد و پيوستگي توابع چند متغيره مشتق هاي
- 9. فصل پنجم:معادلات ديفرانسيل آشنايي معادلات ديفرانسيل معادلات ديفرانسيل جدايي پذير
- 10. فصل ششم: انتگرال انتگرال
- 11. فصل اول: بردارها
- 12. كميتهايي مانند سرعت يا شتاب يك متحرك و نيروي وارد بر يك جسم هنگامي مشخص مي
- 13. برخي از كميت ها هنگامي كه اندازه ي آنها بر حسب واحد مشخصي داده شود كاملا
- 14. 1.1بردارها در صفحه
- 15. 1.1.1تعريف است، يك پاره خط B و انتهاي آن Aكه ابتداي آن AB پاره خط A
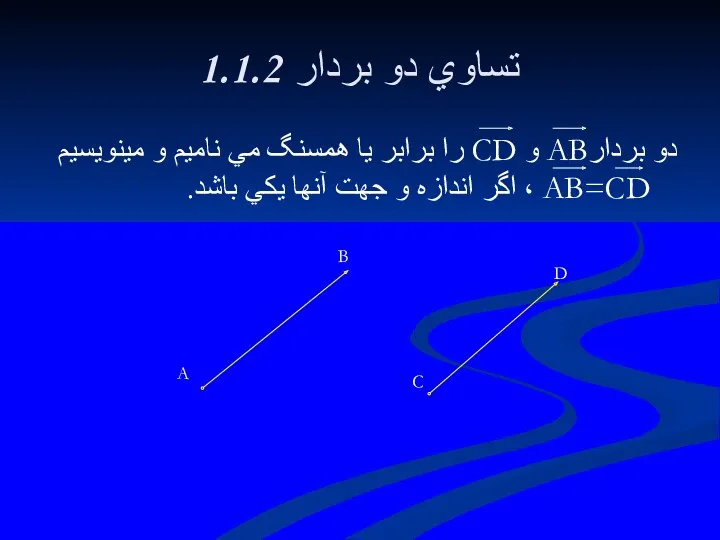
- 16. 1.1.2 تساوي دو بردار دو بردارAB و CD را برابر يا همسنگ مي ناميم و مينويسيم
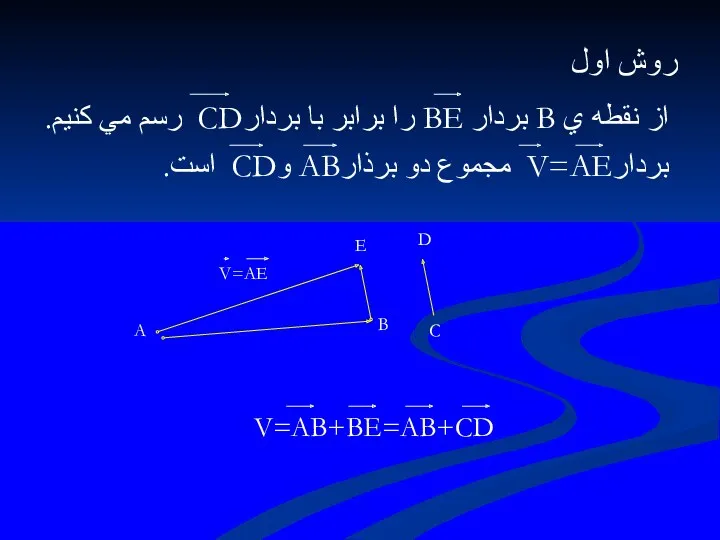
- 17. 1.1.3 جمع بردارها دو بردار AB وCD را در نظر مي گيريم.مجموعAB+CD برداري است مانند V
- 18. روش اول از نقطه ي B بردار BE را برابر با بردارCD رسم مي كنيم. بردارV=AE
- 19. روش دوم از نقطه ي دلخواه P، دو برابرPQ وPR را كه به ترتيب برابر با
- 20. 1.1.4 بردار صفر اگر اندازه ي بردارV برابر صفر باشد يعني V =0 ، بردارV را
- 21. 1.1.5 ضرب عدد در بردا ر(ضرب اسكالر) فرض مي كنيمV برداري دلخواه وC عددي حقيقي باشد.منظور
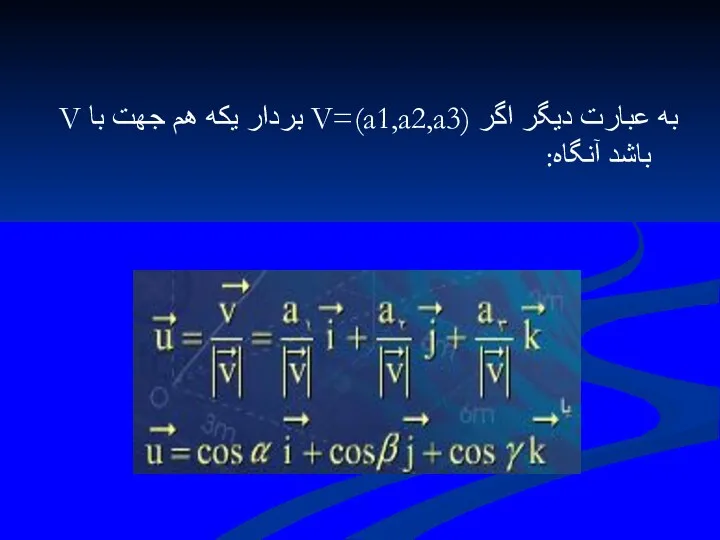
- 22. 1.1.7 تعريف بردارV را كه ابتداي آن مبدا مختصات و انتهاي آن نقطه ي (a1 ,
- 23. 1.11 قضيه اگرV1=(a1,a2) وV2=(b1,b2) دو بردار باشند ، آنگاه مجموع V1+V2 برابر است با: V1+V2= (a1+b1
- 24. 1.1.13 تعريف قرينه ي يك بردار اگرV=(a1,a2)، آنگاه بردار(-a1,-a2) را قرينه ي بردارV مي ناميم و
- 25. 1.1.14 تعريف تفاضل دو بردار بردارV+(-U) را كه مساوي با جمعV با قرينه يU است تفاضلU
- 26. 1.15 تعبير هندسي تفاضل دو بردار نمايش هاي دو بردارV وU را از يك نقطه رسم
- 27. 1.1.16 اندازه ي يك بردار اندازه ي بردار V=(a1,a2) برابر است با: V = a1+a2 2
- 28. 1.1.18 قضيه اگرV وU وW بردارهايي در V بوده وc وd اعدادي حقيقي باشند، آنگاه جمع
- 29. ادامه (cd) V=c (dV) ( قانون شركت پذيري) C (U+V)=cU+cV ( قانون بخشپذيري) (c+d)U=cU+dU ( قانون
- 30. 1.1.20 تعريف فضاي برداري حقيقي فضاي برداري حقيقيV مجموعه اي است از بردارها، همراه با مجموعه
- 31. بردارهاي يكه اندازه ي هر دو بردار (0و1) و(1و0) ، برابر با 1 است، آنها را
- 32. با توجه به نماد گذاري گذشته براي هر بردارV=(a1,a2) به دست مي آوريم: (a1,a2)=a1 (1,0)+a2 (0,1)=a1
- 33. بنابر اين هر بردارV2 در را مي توان به صورت يك تركيب خطي از دو بردارi
- 34. 1.1.25 تعريف توازي بردارها دو بردار نا صفرU وV را موازي مي ناميم ، در صورتي
- 35. 1.1.25 قضيه اگرV بردار نا صفري باشد ، آنگاه U = V 1 v بردار يكه
- 36. 1.2 ضرب عددي دو بردار
- 37. 1.2.1 تعريف ضرب عددي دو بردار اگر U=(a1,a2) وV=(b1,b2) دو بردار درV2 باشند ، آنگاه حاصلضرب
- 38. توجه مي كنيم كه حاصلضرب عددي دو بردار ، عددي حقيقي است و بردار نيست. اين
- 39. 1.2.4 قضيه اگرU وV وW بردارهايي درV2 بوده وc يك اسكالر باشد. آنگاه: U.V=V.U .1 U.(V+W)=U.V+U.W
- 40. 1.2.5 تعريف زاويه ي بين دو بردار فرض مي كنيمU وV دو بردار نا صفر باشند
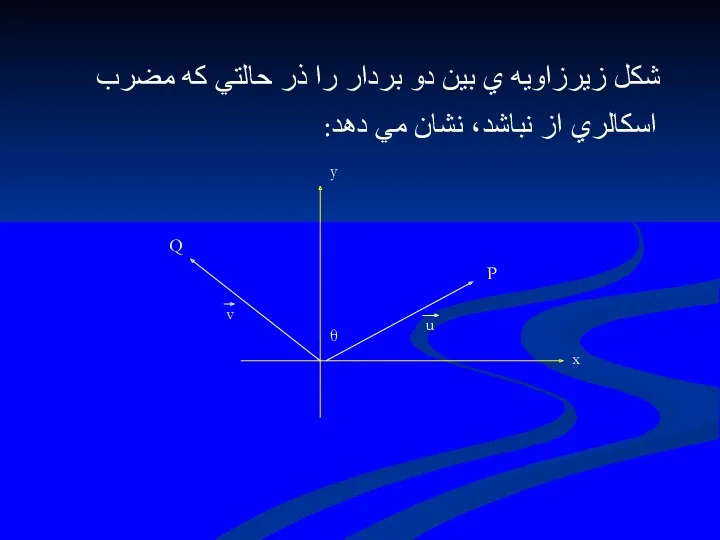
- 41. شكل زيرزاويه ي بين دو بردار را ذر حالتي كه مضرب اسكالري از نباشد، نشان مي
- 42. 1.2.6 قضيه اگر θ زاويه ي بين دو بردارU وV باشد،آنگاه: U.V= U V cos θ
- 43. 1.2.8 نتيجه از قضيه ي قبل نتيجه مي شود كه دو بردارU وV بر هم عمودند
- 44. 1.2.10 تصوير يك بردار بر روي بردار ديگر فرض مي كنيمOP وOQ به ترتيب نمايشگرهاي بردارهاي
- 45. شكل: تصوير بردارV بر روي بردارP x y v u o p Q R θ
- 46. 1.2.11 تعريف اگرU بردار ناصفري باشد، تصوير برداريV روي بردارU به صورت زير تعريف مي كنيم:
- 47. تصوير اسكالرV روي U برابر باV cosθ است . با توجه به قضيه داريم: V cosθ
- 48. 1.3 بردارها در فضاي سه بعدي
- 49. 1.3.1 تعريف مجمو عه ي تمام سه تايي هاي مرتب از اعداد حقيقي را فضاي عددي
- 50. 1.3.2 قضيه فاصله ي بين دو نقطه ( zو yوx) p و ( zو yوx) p
- 51. 1.3.4 تعريف يك بردار در فضاي سه بعدي، يك سه تايي مرتب از اعداد حقيقي به
- 52. اگر بردارهاي يكهi وj وk عبارت باشند از: i=(1,0,0) j=(0,1,0) k=(0,0,1) آنگاه هر بردار در را
- 53. 1.3.5 تعريف سه زاويه يα وβ وδ زوايايي كه بردارV نا صفر به ترتيب با جهت
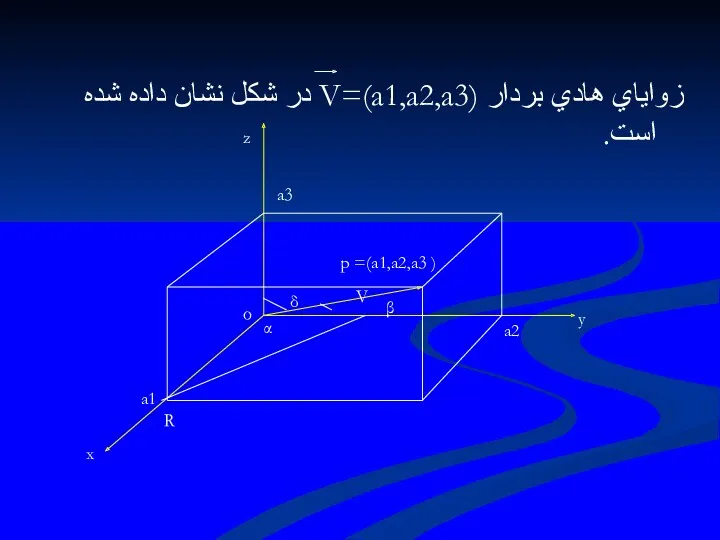
- 54. زواياي هادي بردار (V=(a1,a2,a3 در شكل نشان داده شده است. x y z o R a1
- 55. در شكل مؤلفه هايV اعدادي مثبت و زواياي هادي آن مثبت و كوچكتر2п/ از هستند.به طوري
- 56. مي توان نشاشن داد كه دستور اخير به ازايп п/2 ≤α≤ نيز بر قرار است.دستور هاي
- 57. اعداد α COS و COSβ وδ COS راكسينوسهاي هادي بردارV مي نامند. توجه كنيد كه بردار
- 58. 1.3.7 نكته اگر اندازه ي يك بردار و كسينوسهاي هادي آن معلوم باشند،آنگاه بردار به طور
- 59. 1.3.8 قضيه اگر COS α و COSβ و COS δ كسينوسهاي هادي بردار Vباشند،آنگاه: COS α
- 60. 1.3.15 نتيجه از قضيه و تعريف كسينوسهاي هادي نتيجه مي شمد كه مؤلفه هاي يك بردار
- 61. به عبارت ديگر اگر (V=(a1,a2,a3 بردار يكه هم جهت با V باشد آنگاه:
- 62. در مورد بردارهاي فضايي اعمال جمع ، تفريق،ضرب اسكالر و ضرب عددي دو بردار درV3 ،مشابه
- 63. الف ب
- 64. پ ت
- 65. 1.3.14نكته به آساني مي توان نشان داد كه: 1 0
- 66. 1.3.15قضيه اگرθ زاويه ي بين دو بردار نا صفرU وV درV3 باشد آنگاه:
- 67. 1.3.16تعريف دو بردار درV3 را موازي مي ناميم اگر و تنها اگر يكي از بردارها مضرب
- 68. 1.3.17قضيه دو بردار نا صفر درV3 موازي اند اگر و تنها اگر زاويه ي بين آنها0
- 69. 1.3.18قضيه دو بردار نا صفرU وV درV3 متعامدند اگر و تنها اگر U.V=0
- 70. 1.4ضرب برداري بردارها
- 71. 1.4.1تعريف اگر U=(a1,a2,a3) و V=(b1,b2,b3) آنگاه حاصل ضرب برداريU درV با نشانU*V مي دهيم.برداري است كه
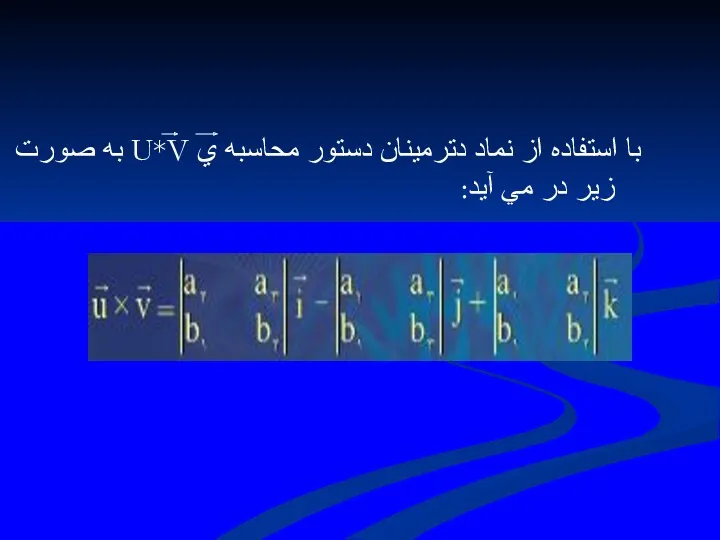
- 72. براي سهولت در يادگيري و به ذهن سپردن دستور U*V ، از نماددترمينين استفاده مي كنيم.يك
- 73. با استفاده از نماد دترمينان دستور محاسبه ي U*V به صورت زير در مي آيد:
- 74. سمت راست عبارت اخير را مي توان با نماد زير نشان داد:
- 75. 1.4.3قضيه اگرU وV بردارهايي درV3 باشند، آنگاه: U*V= - (V*U)
- 76. 1.4.4قضيه اگرi وj وk بردارهاي يكه يV3 باشند، آنگاه:
- 77. 1.4.5قضيه اگرU وV وW بردارهايي درV3 وc يك اسكالر باشد آنگاه:
- 78. 1.4.7قضيه اگرU وV دو بردارV3 وθ زاويه ي بينU وV باشد،آنگاه: U*V = U V sinθ
- 79. 1.4.9نتيجه اگرU وV دو بردار نا صفر درV3 باشند آنگاه و موازي اند اگر و تنها
- 80. 1.4.11قضيه اگرU وV وW سه بردار درV3 باشند، آنگاه:
- 81. 1.4.12تعريف فرض مي كنيم U=(a1,a2,a3) و V=(b1,b2,b3)و =(c1,c2,c3) W. حاصلضربU.(V*W) را حاصلضرب عددي سه گانه بردارهاي
- 82. حاصلضرب عددي سه گانه برابر است با:
- 83. حاصلضرب عددي سه گانه يك اسكالر است.
- 84. 1.4.13قضيه اگرU وV دو بردار نا صفر در باشند آنگاه:
- 85. 1.5بردارهاي فضاي n بعدي
- 86. 1.5.1تعريف فرض كنيدn عدد صحيح مثبتي باشد، n تايي مرتب (x1,x2…,xn)مجموعه اي ازn عدد است كه
- 87. اعداد حقيقي xn,……,x2,x1 را به ترتيب مؤلفه هاي اول تا nام اينn تايي مرتب مي خوانيم.مجموغه
- 88. دو تايي مرتبY=(y1,y2,…yn) وX=(x1,x2,…xn) را برابر مب ناميم اگر و تنها اگر براي هرi=1,2,…n داشته باشيم:
- 89. 1.5.3تعريف فرض مي كنيمU=(a1,a2,…an) وV=(b1,b2,…bn) دو بردار درVn وc عدد حقيقي (اسكالر) باشد.
- 90. مجموع دو بردار و ضرب اسكالر عدد در بردار به صورت زير تعزيف مي شود: U+V=(a1+b1,a2+b2,…,an+bn)
- 91. 1.5.4قضيه فرض مي كنيم U وV و W سه بردار درVn وc وk دو اسكالر (عدد
- 92. ب) جمع بردارها شركت پذير است، يعني (U+V)+W=U+(V+W) پ)عمل جمع داراي عضو خنثي است يعني بردار0=(0,0,…,0)
- 93. ت) براي هرU بردار قرينه U – وجود دارا به طوري كه U+(-U)=0 ث)c (U+V)=c U
- 94. 1.5.5تعريف طول بردار U=(a1,a2,…an) برابر است با
- 95. فصل دوم:ماتريس و دترمينان
- 96. در اين فصل با معرفي ماتريس مفهوم بردار را تعميم مي دهيم.همچنين انواع ماتريس،ماتريسهاي خاص و
- 97. 2.1ماتريس
- 98. 2.1.1تعريف هر جدولي از اعداد را كه شامل m سطر وn ستون باشد،يك ماتريس mدرn مي
- 99. هر يك از اعدادaij را يك عنصر يا درايه ماتريس مي ناميم.در اينجاi انديس سطر وj
- 100. 2.1.2تعريف الف)هر گاه ماتريسA=(aij)mn تنها داراي يك سطر باشد،يعنيm=1 ،اين ماتريس را يك ماتريس سطري (بردار
- 101. اگر ماتريس A=(aij)mn تنها داراي يك ستون باشد.يعني n=1،اين ماتريس را يك ماتريس ستوني (بردار ستوني)مي
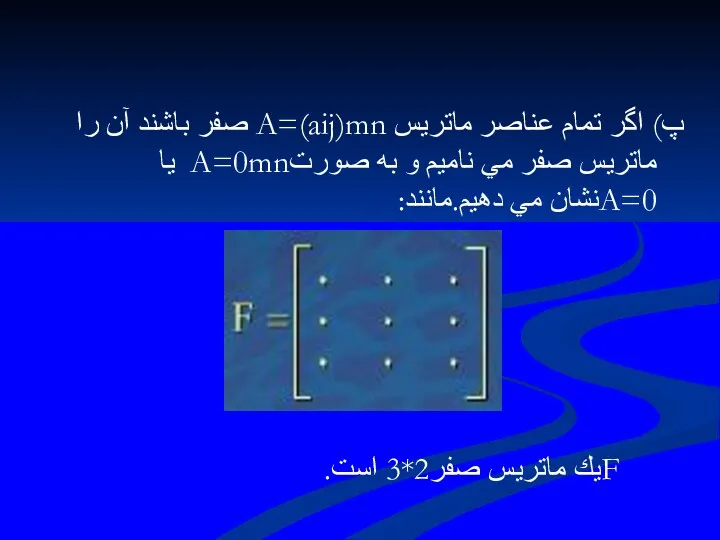
- 102. پ) اگر تمام عناصر ماتريس A=(aij)mn صفر باشند آن را ماتريس صفر مي ناميم و به
- 103. 2.1.3تعريف ماتريسي را كه تعداد سطرها و تعداد ستونهايش برابر باشد، يك ماتريس مربع مي ناميم.به
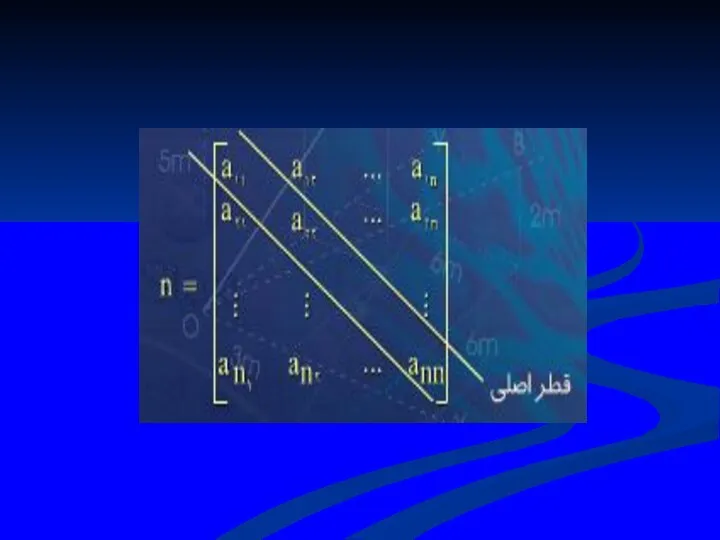
- 104. در ماتريس مربع A=(aij)mn ،قطري را كه شامل عناصر a11,a22,…,ann قطر اصلي و اين عناصر را
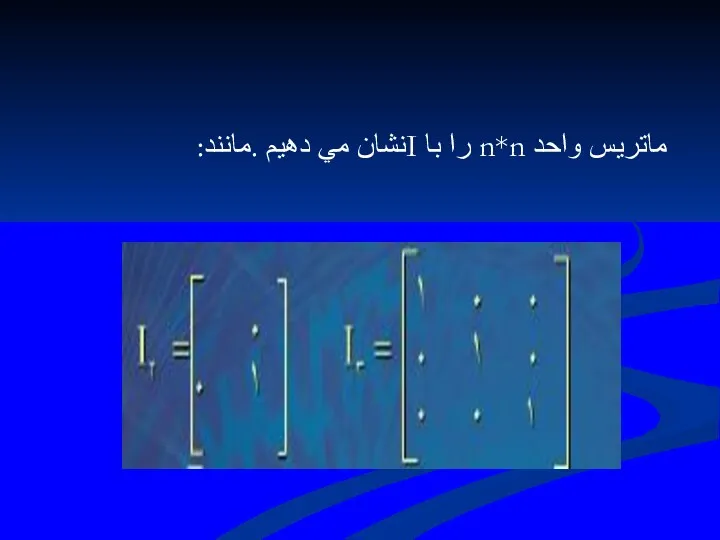
- 106. 2.1.4تعريف ماتريس مربع A=(aij)mn را يك ماتريس هماني يا واحدn*n مي ناميم اگر هر يك از
- 107. ماتريس واحد n*n را با Iنشان مي دهيم .مانند:
- 108. 2.1.5تعريف تساوي دو ماتريس دو ماتريس A=(aij)mn و B=(bij)pq را برابر مي گوييم اگر m=pوn=q و
- 109. براي مثال:
- 110. 2.1.7تعريف فرض مي كنيم A=(aij)mn و B=(bij)mn دو ماتريس m*nوk عددي حقيقي باشد.
- 111. الف) حاصل جمع اين دو ماتريس را باA+B نشان داده و به صورت زير تعريف مي
- 112. ب)حاصل ضرب عدد حقيقيk درA ماتريس را باkA نشان داده و به صورت زير تعريف مي
- 113. توجه كنيد كه A+B و kA ماتريسهاي m*n هستند.توجه داشته باشيد كه جمع دو ماتريس كه
- 114. 2.1.9تعريف اگر A=(aij)m0 ماتريس A (1-) را قرينه ي ماتريس A مي ناميم و با A=(-aij)m0
- 115. 2.1.11قضيه اگرA وB وC سه ماتريسm*n وk وh دو عدد حقيقي باشند آنگاه:
- 116. 2.1.13تعريف ماتريسهاي A=(aij)mp و B=(bij)pn را در نظر مي كيريم.منظور از حاصل ضربA درB ماتريسm*n اي
- 117. 2.1.15قضيه اگر A=(aij)mn يك ماتريس مربعيn*n باشد آنگاه:
- 118. 2.1.16قضيه اگر A=(aij)mpو B=(bij)pq و C=(cij)qn آنگاه A(BC)=(AB)C
- 119. 2.1.19قضيه اگر A=(aij)pnو B=(bij)pn و C=(cij)mp C(A+B)=CA+CB
- 120. 2.1.20تعريف اگر در ماتريس A=(aij)mn جاي سطرها و ستونها را با يكديگر عوض كنيم، ماتريس حاصل
- 121. 2.1.21قضيه اگرA وB دو ماتريسm*nوk عددي حقيقي باشد آنكاه: الف) (A)=Aيعني ترانهاده ، ترانهاده ماتريس با
- 122. پ) (A+B) = A+ B،يعني ترانهاده مجموع دوماتريس با مجموع ترانهاده هاي دو ماتريس برابر است.
- 123. 2.1.23تعريف الف) ماتريس مربع A را متقارن مي ناميم اگر A= A . براي مثال ماتريس
- 124. ب) ماتريس A مربع را شبه متقارن مي ناميم اگرA=A . اگر يك ماتريس شبه متقارن
- 125. پ) ماتريس A مربع را قطري مي ناميم اگر همه ي عناصر غير واقع بر قطر
- 126. ت) ماتريس قطري S را يك ماتريس اسكالر مي ناميم، اگر عناصر قطر اصلي آن برابر
- 127. ث) ماتريس n*n وc را متعامد مي گوييم اگر :
- 128. براي مثال: آنگاه پسc ماتريسي متعامد است.
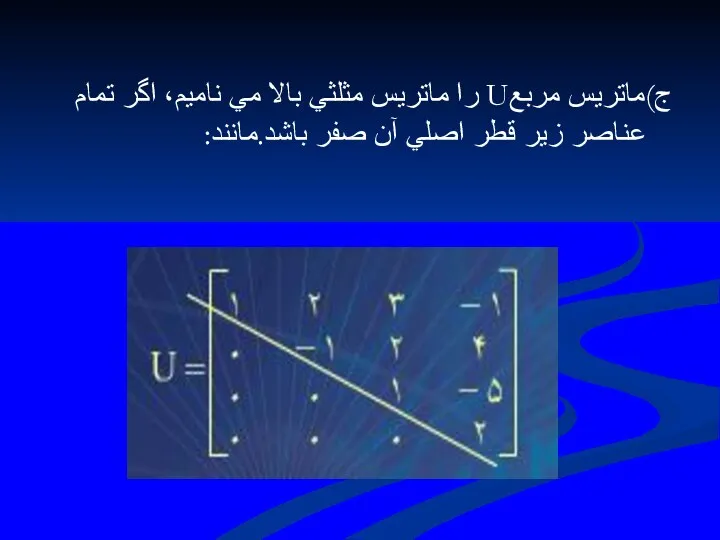
- 129. ج)ماتريس مربعU را ماتريس مثلثي بالا مي ناميم، اگر تمام عناصر زير قطر اصلي آن صفر
- 130. چ)ماتريس مربع Lرا ماتريس مثلثي پايين مي ناميم، اگر تمام عناصر بالاي قطر اصلي آن صفر
- 131. 2.1.25تعريف در ماتريس مربع A=(aij)nn مجموع تمام قطر اصلي را اثر A مي ناميم و باtr(A)
- 132. 2.2 دترمينان
- 133. دترمينان ماتريسA را باdet A ياA نشان مي دهيم.
- 134. 2.2.1تعريف 1) ماتريس 1*1 تنها داراي يك عنصرa11 است، دترمينان اين ماتريس را برابر با عدد
- 135. 2) دترمينان ماتريس 2*2 به صورت زير تعريف مي شود Det A= A = = a11a22-a12a21
- 136. 2.2.2تعريف ماتريس A=(aij)nn را در نظر مي گيريم. فرض كنيد Mij ماتريسي(n-1)*(n-1) باشد كه از حذف
- 137. 2.2.3تعريف همسازه عنصر aij در ماتريس A=(aij)nn را با Aij نشان مي دهيم وبرابر با عدد
- 138. 2.2.4تعريف دترمينان ماتريس A=(aij)nn را به صورت تعريف مي كنيم.مي گوييم دترمينيانA بر حسب سطرi ام
- 139. بنابر اين تعريف براي محاسبه ي دترمينان يك ماتريس، يك سطر يا يك ستون را انتخاب
- 140. اگر دترمينان را بر حسب سطر يا ستوني كه بيشترين تعداد صفر را دارد محاسبه مي
- 141. 2.2.7قضيه(خواص دترمينان) 1) دترمينان ماتريس مربع A و ترانهادهA برابر است .يعني: A = A 2)
- 142. 3) اگر تمام عناصر يك سطر يا يك ستون ماتريس A در عددr ضرب مي كنيم
- 143. 5) اگر دو سطر يا دو ستون ماتريسي برابر باشند، آنگاه مقدار دترمينان آن برابر با
- 144. 7) دترمينان حاصلضرب دو ماتريس برابر با حاصلضرب دترمينانهاي آنها است يعني AB = A B
- 145. 2.2.15تعريف اگر دترمينان ماتريس A=(aij)nn برابر صفر باشد ، ماتريس A را منفرد مي ناميم. در
- 146. 2.3وارون ماتريس
- 147. 2.3.1تعريف ماتريس A=(aij)nn را وارون پذير مي ناميم ، اگر ماتريسي مانند B=(bij)nn وجود داشته باشد
- 148. 2.3.5اعمال سطري مقدماتي ماتريس A=(aij)nn را در نظر مي كيريم. هر يك از اعمال زير را
- 149. براي اختصار در نوشتن اعمال سطري مقدماتي ، از حرفR ، اول كلمه ي Rowبه معناي
- 150. 2.3.8قضيه اگر ماتريس وارون پذير A به وسيله ي يك سلسله اعمال مقدماتي تبديل به ماتريس
- 151. براي به دست آوردن وارون ماتريس A معمولا اعمال سطري مقدماتي را به طور هم زمان
- 152. 2.3.11تعريف ترانهاده ماتريس همسازه هاي ماتريس مربع A را ماتريس الحاقي A مي ناميم و با
- 153. 2.3.13قضيه اگر A يك ماتريسn*n باشد آنگاه :
- 154. 2.3.13قضيه اگرdetA=0 ،آنگاه وارون وجود دارد و برابر است با عكس اين نتيجه نيز درست است.يعني
- 155. 2.3.17قضيه اگرA وB دو ماتريس مربع n*n و وارون پذير باشند آنگاه الف) ماتريس حاصلضرب وارون
- 156. پ) وارون ماتريس وارونA برابرA است ، يعني ت) دترمينان وارون ماتريس A برابر با معكوس
- 157. فصل سوم: دستگاه معادلات خطي و توابع خطي
- 158. در اين فصل با استفاده از مفهوم ماتريس و دترمينان روشي براي حل و بحث در
- 159. 3.1دستگاه معادلات خطي
- 160. معادله اي به صورت a1x1+a2x2+…+anxn=0 با مجهول xn,…,x2,x1را يك معادله ي n مجهولي خطي مي ناميم.
- 161. 3.1.1تعريف مجموعه اي از معادلات خطي را يك دستگاهm معادله ي خطيn مجهولي مي ناميم.
- 162. تايي از اعداد حقيقي را در تمام معادله هاي دستگاه صدق كند يك جواب اين دستگاه
- 163. اين دستگاه را ميتوان به صورت معادله ي ماتريسي زير نوشت:
- 164. با فرض معادله ي ماتريسي اخير به صورت خلاصه ي زير در مي آيد. AX=B Aرا
- 165. توجه كنيد يك دستگاه معادلات خطي ممكن است داراي يك جواب منحصر به فرد يا بينهايت
- 166. اينك به معرفي روشهايي براي حل يك دستگاه معادلات خطي مي پردازيم. 1- روش حذف گوسي
- 167. 3.1.2روش حذف گوسي ميتوان نشان داد دو دستگاه معادلات خطي كه يكي از آنها به وسيله
- 168. ضرب يك معادله ي دستگاه در عددي غير صفر. تعويض محل دو معادله ي دستگاه و
- 169. پس براي حل دستكاه AX=B بايد تا جايي كه ممكن است به وسيله ي اعمال سطري
- 170. 3.1.6قضيه اگر تعداد مجهولها با تعداد معادله ها ي يك دستگاه معادلات خطي برابر باشد (دستگاهn
- 171. 3.1.8دستور كرامر اگر ضرايب يك دستگاهn معادلاتn مجهولي وارون پذير باشد آنگاه جواب دستگاه برابر است
- 172. 3.1.10تعريف اكر در دستگاهm معادله يn خطي مجهولي طرف دوم تمام معادلات صفر باشند دستگاه را
- 173. روشن است كه در دستگاه همگن هموارهx1=x2=…=xn=0 يك جواب دستگاه هست. اين جواب به جواب بديهي
- 174. 3.1.11قضيه دستكاهn معادله ي خطيn مجهولي همگن داراي يك جواب غير بديهي ( غير صفر) است.
- 175. 3.1.13نتيجه يك دستگاه m معادله يn خطي مجهولي همگن همواره داراي يك جواب غير بديهي (
- 176. 3.1.15قضيه اگرX1 وX2 دو جواب دستگاه غير همگن AX=B باشند آنگاهX2-X1 جوابي براي دستگاه همگن AX=0
- 177. 3.1.13نتيجه دستگاه غير همگن AX=B داراي يك جواب منحصر به فرد است اگر و تنها اگر
- 178. 3.2استقلال و وابستگي خطي
- 179. 3.2.1تعريف مجموعه يm بردار{V1,V2,…,Vn} از عناصر فضاي برداري R را مستقل خطي مي ناميم اگر هيچ
- 180. به بيان ديگر مجموعه يm بردار{V1,V2,…,Vn} مستقل خطي است تنها جواب معادله ي برابر با c1=c2=…=cm=0
- 181. 3.3رتبه ي يك ماتريس
- 182. در اين بخش به هر ماتريس عدد صحيح و مثبتي به نام رتبه ي ماتريس را
- 183. 3.3.1تعريف فرض كنيمA ماتريسيm*n باشد. حداكثر تعداد سطرهاي مستقل خطي ماتريسA را رتبه ي ماتريسA مي
- 184. به عبارت ديگر اگرR1,R2,…,Rm سطرهاي ماتريسA باشند رتبه يa برابر با حداكثر تعداد بردارهاي مستقل خطي
- 185. يك روش تعيين رتبه ي ماتريسA اين است كه بزرگترين زير ماتريس مربع A را كه
- 186. 3.3.6خواص رتبه ي ماتريس الف) رتبه ي ماتريس واحدIn برابر باn است، يعني: ب) رتبه ي
- 187. پ) اگر A ماتريس n*nباشد آنگاهr(A)=n اگر و تنها اگرdet A=0 به بيان ديگرr(A) det A=0
- 188. 3.3.7نتيجه اينك با استفاده از مفهوم رتبه ي ماتريس به طور خلاصه به بررسي جوابهاي دستگاه
- 189. الف) اگرr(A B)=r(A) آنگاه دستگاه داراي حداقل يك جواب است. ب) اگر r(A B)=r(A)=n آنگاه دستگاه
- 190. 3.4توابع خطي
- 191. در اين بخش به مطالعه ي توابع خطي كه توابعي از يك فضاي برداري به فضاي
- 192. 3.4.1تعريف تابع n متغيره يf از فضاي برداريR به فضاي برداري R را كه به ازاي
- 193. 3.4.3قضيه تابعf: R R خطي است.اگر و تنها اگر هر مؤلفه مقدا رتابع fدر به صورت
- 194. از اين قضيه نتيجه مي شود كه اگرf : R R تابع خطي با شد آنگاه
- 195. بنا بر اينA=(aij)m*n قرار دادن مقدار تابع خطيf را ميتوان به ازاي هرx R به صورت
- 196. 3.4.6تعريف تابعF : R R را كه براي هر به صورت زير تعريف مي شود، تابع
- 197. 3.4.7تعريف تابعI: R R را كه براي هرX Є R به صورت n n n
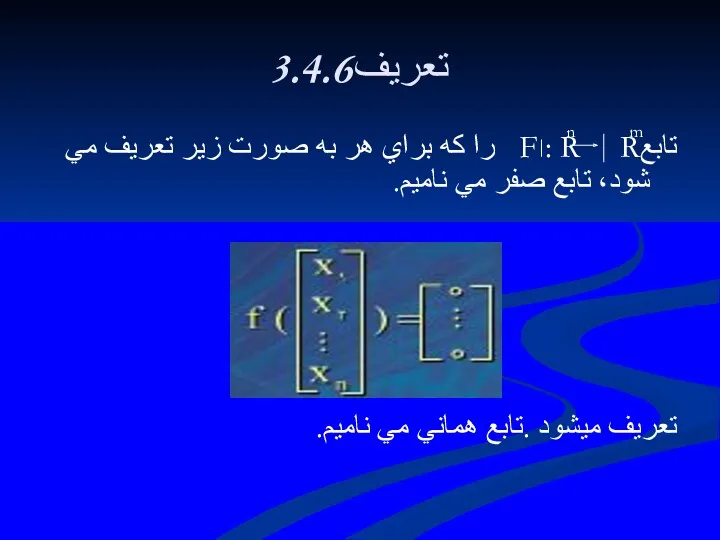
- 198. 3.4.8تعريف توابع خطي f : R R و g : R R را در نظر مي
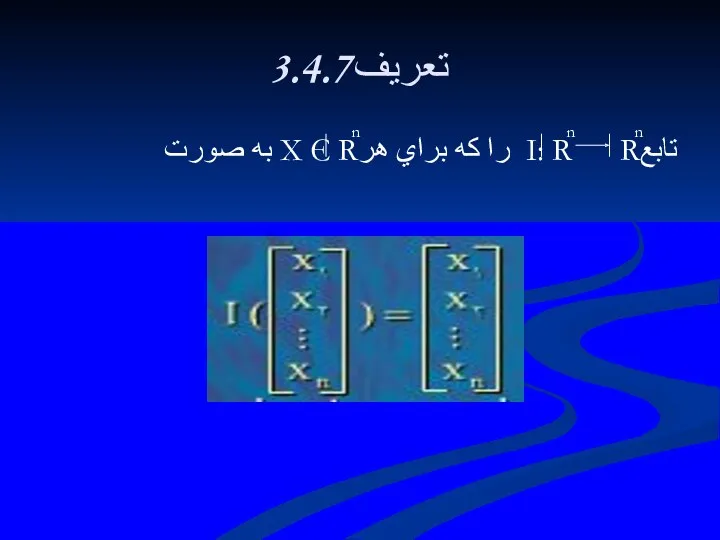
- 199. فصل چهارم:توابع چند متغيره
- 200. در فصل هاي قبل با توابعي سر و كار داشتيم كه تنها وابستهبه يك متغير بودند.
- 201. فرض كنيد هزينه ي ماهانه ي خانواده اي بستگي به مقدار مصرف آنها از مواد غذايي،پوشاك،خدمات
- 202. 4.1توابع چند متغيره
- 203. تابعf كه قلمرو آن زير مجموعه اي ازR و برد آن زير مجموعه اي از اعداد
- 204. اگرf يك تابعn متغيره باشد هر عنصر قلمرو آن ،n تايي (x1.x2,…,xn)است ، مقدار تابع به
- 205. 4.1.3تعريف اگرf,g دو تابع n متغيره باشند آنگاه براي هرx ازR و هر عدد حقيقي k،
- 206. 4.2حد و پيوستگي توابع چند متغيره
- 207. 4.2.1تعريف فرض مي كنيم f يك تابع دو متغيره باشد مي گوييم حد تابع f در
- 208. مي توان نشان داد كه عدد حقيقيL در صورت وجود منحصر به فرد است و لذاL
- 209. حد توابع سه متغيره و به طور كليn متغيره نيز به همين صورت تعريف مي شود.تمام
- 210. 4.2.2قضيه اگرf(x,y)=x , g(x,y)=y آنگاه الف)
- 211. ب)اگرk(x,y)=k تابعي ثابت باشد آنگاه Lim k(x,y)=k (x,y) (a,b) كه در آنk عددي ثابت است.
- 212. 4.2.3قضيه اگر حد تابع دو متغيره يf در نقطه ي(a,b) برابرL باشد آنگاه
- 213. اين قضيه بيان مي كند كه اگر lim f(x.y)=L آنگاه حد تابع f وقتي كه نقطه
- 214. 4.2.5قضيه اگر حد تابعf هنگامي(x,y) كه بر روي دو منحني متمايز به نقطه ي(a,b) نزديك مي
- 215. 4.2.6نتيجه اگر آنگاه تابع f در نقطه ي(a,b) حد ندارد.
- 216. توجه كنيد در ابتداx را ثابت فرض كرده را در صورت وجود محاسبه مي كنيم.سپس حد
- 217. 4.2.8قضيه اگر حد توابع دو متغيره يf وg در نقطه ي (a,b) اگر حد توابع دو
- 218. 2)براي هر عدد ثابتk
- 219. 3)حد تفاضل دو تابع برابر با حدهاي آنهاست يععني:
- 220. 4)حد حاصلضرب دو تنبع برابر با حاصلضرب حدهاي آنهاست.يعني:
- 221. 5) حد خارج قسمت دو تابع برابر با خارج قسمت حدهاي آنهاست مشروط بر اينكه حد
- 222. 4.2.10قضيه اگر و تابع يك متغيرهg درL پيوسته باشد آنگاه:
- 223. 4.2.12تعريف تابع دو متغيره يf را در نقطه ي (a,b) پيوسته مي ناميم اگر شرايط زير
- 224. 3) در صورتي كه يكي از اين شرايط بر قرار نباشد تابع f را در نقطه
- 225. 4.2.14قضيه اگر توابع دو متغيره ي f وg در نقطه ي (a,b) پيوسته باشند آنگاه تواب
- 226. 4.2.16قضيه اگر تابع دو متغيره ي f در نقطه ي (a,b) و تابع يك متغيره يg
- 227. 4.3مشتقهاي جزئي
- 228. در اين بخش مفهومي نزديك به مفهوم مشتق توابع يك متغيره را در مورد توابع چند
- 229. 4.3.1تعريف فرض مي كنيمf تابعي از دو متغيرx وy باشد. اگر وجود داشته باشد مقدار اين
- 230. به همين ترتيب مشتق جزيي تابع f نسبت به متغيرy در نقطه ي(x,y) به صورت تعريف
- 231. اگر f (x,y) وجود داشته باشد f تابعي از دو متغيرx وy است اين تابع را
- 232. در اينجا نماد ∂ را به جايd برتي تمايز مشتقهاي جزيي از مشتق معمولي به كار
- 233. به همين ترتيب در محاسبه ي f (x,y) متغير را در تابعf(x,y) ثابت در نظر گرفته
- 234. 4.3.4مشتقهاي جزيي مرتبه هاي بالاتر نظير مفهوم مشتقهاي مرتبه هاي بالاتر براي توابع يك متغيره مي
- 235. اين مشتقها را مشتقهاي جزيي مرتبه دوم تابع f مي ناميم. مشتقهاي جزيي مرتبه دوم تابع
- 236. لازم به تذكر است كه ترتيب نوشتن متغيرهايx وy در f بر خلاف ترتيب آنها در
- 237. 4.3.6قضيه فرض مي كنيم f تابعي با متغير هاي x وy باشد. اگر توابع f و
- 238. 4.4ديفرانسل كل و مشتقگيري ضمني
- 239. 4.4.1تعريف فرض مي كنيم f تابعي با متغير هاي x وy باشد. اگر مشتقهاي جزيي مرتبه
- 240. ديفرانسيل كل تابع بيش از دو متغيره نيز به همين ترتيب تعريف مي شود، اگرu تابعي
- 241. 4.4.3نكته فرض مي كنيم f تابعي با متغير هاي x وy باشد. اگر متغير هاي x
- 242. 4.4.6تعريف فرض مي كنيم f تابعي با متغير هاي x وy باشد. اگر مشتقهاي جزيي مرتبه
- 243. 4.4.8قاعده زنجيري براي توابع چند متغيره فرض مي كنيم f تابعي با متغير هاي x وy
- 244. قاعده زنجيري براي توابع بيش از دو متغير كاملا مشابه است.
- 245. 4.4.10مشتقگيري ضمني به كمك مفهوم مشتقهاي جزيي مي توان دستور ساده اي براي مشتقگيري از توابع
- 246. فرض مي كنيم معادله يf(x,y)=0 ،متغيرy را به صورت تابعي ازx به طور ضمني تعريف كند،
- 247. 4.4.12مشتقهاي جزيي توابع ضمني فرض مي كنيم تابع دو متغيره يz=f(x,y) در معادله ي F(x,y,z)صدق كند.پس
- 248. به همين ترتيب به دست مي آوريم مشروط بر اينكه ∂F/∂x=0
- 249. 4.5ماكسيمم و مينيمم توابع دو متغيره
- 250. همهنطور كه از مشتقهاي اول و دوم يك تابع يك متغيره براي تعيين ماكسيمم و مينيمم
- 251. 4.5.1تعريف فرض مي كنيم f تابعي با متغير هاي x وy باشد. در اين صورت: الف)
- 252. ب) f(a,b) مقدارمينيمم (مطلق) fمي ناميم. اگر براي هر(x,y) از قلمروf داشته باشيم: F(x,y)>=f(a,b)
- 253. 4.5.2تعريف فرض مي كنيم f تابعي با متغير هاي x وy باشد. در اين صورت: الف)
- 254. ب) مي گوييمf تابع در(a,b) داراي يك مينيمم نسبي است. اگر دايره به مركز (a,b) در
- 255. 4.5.4قضيه فرض مي كنيم تابع دو متغيره fدر(a,b) يك ماكسيمم يا مينيمم نسبي دارد.اگر مشتقهاي جزيي
- 256. از اين قضيه نتيجه مي شود كه اگر تابع fدر(a,b) يك ماكسيمم يا مينيمم نسبي داشته
- 257. هر جواب اين دستگاه را (نظير توابع يك متغيره ) يك نقطه ي بحراني تابع f
- 258. اگر Fy(a,b) Fx(a,b)= ولي تابع F در((a,b ماكسيمم يا مينيمم نسبي نداشته باشد مي گوييم تابع
- 259. معمولا با استفاده از تعريف تشخيص اينكه يك نقطه ي بحراني تابع دو دو متغيره ي
- 260. 4.5.8آزمون مشتق دوم فرض مي كنيم f تابعي با متغير هاي x وy باشد.و Fy(a,b)=0 Fx(a,b)=
- 261. در اين صورت الف) اگر(a,b)>0 ∆ وFxx(a,b) ب) اگر(a,b)>0 ∆ وFxx(a,b)>0 آنگاه F در(a,b)مينيمم نسبي دارد.
- 262. پ) اگر(a,b)>0 ∆ آنگاه F در(a,b)يك نقطه ي زين اسبي دارد . به عبارت ديگر ماكسيمم
- 263. دقت كنيد كه اگر(a,b)>0 ∆ آنگاه حاصلضرب fxx(a,b)fyy(a,b) مثبت است.پس fxx(a,b)وfyy(a,b) هم علامت مي باشند .در
- 264. 4.6ماكسيمم و مينيمم توابع نسبت به شرايط داده شده
- 265. در اكثر مسايل مديريت و اقتصاد تعيين ماكسيمم و مينيمم يك تابع چند متغيره با توجه
- 266. براي مثال فرض كنيد هدف يك مصرف كننده به حداكثر رسانيدن مطلوب در مصرف دو كالاي
- 267. يكي از محدوديتها ميزان درآمد او است. پس مطلوب است اين مصرف كننده تابغي از ميزان
- 268. پس بايد ماكسيمم تابع U=f(x1,x2) را نسبت به شرط (محدوديت) P1x1+p2x2=y پيدا كنيم كه در آن
- 269. به دو روش مي توان اين كار را انجام داد. يكي به روش جايگزيني و ديگري
- 270. 4.6.1روش جايگزيني يكي از روشهاي به دست آوردت ماكسيمم و مينيمم توابع نسبت به شرايط داده
- 271. 4.6.3روش لاگرانژ ميخواهيم ماكسيمم يا مينيمم تابع دو متغيره يf(x,y) را با محدوديتg(x,y)=0 بيابيم.متغير جديدλ موسوم
- 272. پس اگر fدر (a,b)ماكسيمم يا مينيمم داشته باشيم آنگاه 0λ= λ وجود دارد به طوري كه(a,b,
- 273. 4.6.5شرط كافي براي وجود ماكسيمم و مينيمم توابع نسبت به شرايط داده شده فرض مي كنيم
- 274. الف) ماكسيمم اين است كه
- 275. ب) مينيمم اين است كه
- 276. 4.6.6نكته روش لاگرانژ را ميتوان براي تابعn متغيرهf(x1,x2,…,xn) با تابع محدوديت gi(x1,x2,…,xn) i=1,2,…,nكه در آن تعميم
- 277. در اين صورت تابع لاگرانژ عبارتند از از مساوي صفر قرار دادن مشتقهاي جزيي تابع لاگرانژ
- 278. فصل پنجم:معادلات ديفرانسيل
- 279. حل برخي از مسايل در مديريت ئ اقتصاد منجر به بررسي معادله اي بين يك تابع
- 280. 5.1آشنايي با معادلات ديفرانسيل
- 281. 5.1.1تعريف فرض كنيدy تابعي ازx باشد هر معادله اي به صورتF(x,y,y,…,y ) را كهF در آن
- 282. توجه كنيد منظورy از مشتق n ام y نسبت بهx است و مرتبه ي يك معادله
- 283. 5.1.2تعريف تابع y=f(x) را يك جواب معادله ي ديفرانسيل F(x,y,y,…,y )=0 در فاصله يI مي ناميم.در
- 284. مجموعه ي تمام جوابهاي معادله را جواب عمومي معادله مي ناميم. منظور از حل يك معادله
- 285. 5.1.4تعريف معادله ي ديفرانسيل مرتبه ي ام با شرايط اوليه را كه در آن ها اعداد
- 286. توجه كنيد كه براي معادله ي ديفرانسيل مرتبه ي nامn شرط اوليه وجود دارد .اين شرايط
- 287. 5.1.7تعريف يك معادله ي ديفرانسيل با مشتقات جزيي معادله ايست كه شانل يك تابع مجهول چند
- 288. 5.2معادلات ديفرانسيل جدايي پذير
- 289. در اين بخش روش حل معادلات ديفرانسيلي را بررسي مي كنيم كه مي توان متغيرهاي آنها
- 290. 5.2.1تعريف معادله ي ديفرانسيل مرتبه ي اول p(x)dx+q(y)dy=0 را كه در آنp وq دو تابع حقيقي
- 292. Скачать презентацию





















































































































































































































































































 Прямоугольный треугольник. Признаки равенства прямоугольных треугольников
Прямоугольный треугольник. Признаки равенства прямоугольных треугольников Үш таңбалы сандарды ауызша қосу және азайту. Матем (1-т)
Үш таңбалы сандарды ауызша қосу және азайту. Матем (1-т) Математика 4 класс устный счет
Математика 4 класс устный счет Действительные числа. 10 класс
Действительные числа. 10 класс Смежные и вертикальные углы. 7 класс
Смежные и вертикальные углы. 7 класс Умножаем и делим
Умножаем и делим Симметрия в природе
Симметрия в природе Стандартный вид одночлена. 7 класс
Стандартный вид одночлена. 7 класс Измерение углов
Измерение углов Приёмы умножения числа 2. Деление на 2
Приёмы умножения числа 2. Деление на 2 Решето Эратосфена
Решето Эратосфена Решение задач с помощью квадратных уравнений
Решение задач с помощью квадратных уравнений Презентация к занятию внеурочной деятельности по математике Как люди научились считать (3 класс)
Презентация к занятию внеурочной деятельности по математике Как люди научились считать (3 класс)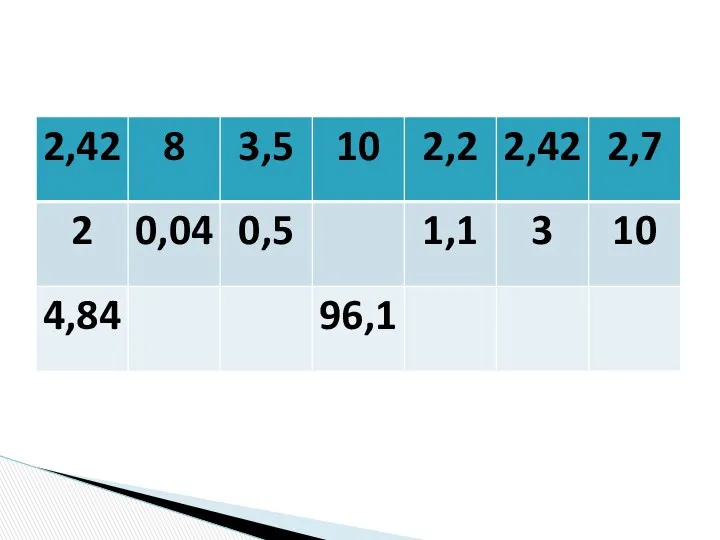 Умножение десятичных дробей
Умножение десятичных дробей Урок математики в 9 классе с элементами краеведения
Урок математики в 9 классе с элементами краеведения Решение уравнений. Система заданий по математике. 6 класс
Решение уравнений. Система заданий по математике. 6 класс Осевая и центральная симметрии. §44
Осевая и центральная симметрии. §44 Случайные величины. Дискретная случайная величина
Случайные величины. Дискретная случайная величина Решение треугольников
Решение треугольников Сложение и вычитание положительных и отрицательных чисел. 6 класс
Сложение и вычитание положительных и отрицательных чисел. 6 класс Взаимосвязь сложения и вычитания
Взаимосвязь сложения и вычитания Равнобедренный треугольник
Равнобедренный треугольник Платоновы тела
Платоновы тела Объём фигуры. Единицы объёма
Объём фигуры. Единицы объёма Графические диктанты
Графические диктанты Математические и структурные модели управления
Математические и структурные модели управления Сложение и вычитание десятичных дробей. Решение задач
Сложение и вычитание десятичных дробей. Решение задач Наслідки з теореми косинусів
Наслідки з теореми косинусів