Содержание
- 2. Уравнение линии на плоскости Линия – это множество точек плоскости, обладающих определенным свойством. Уравнением линии l
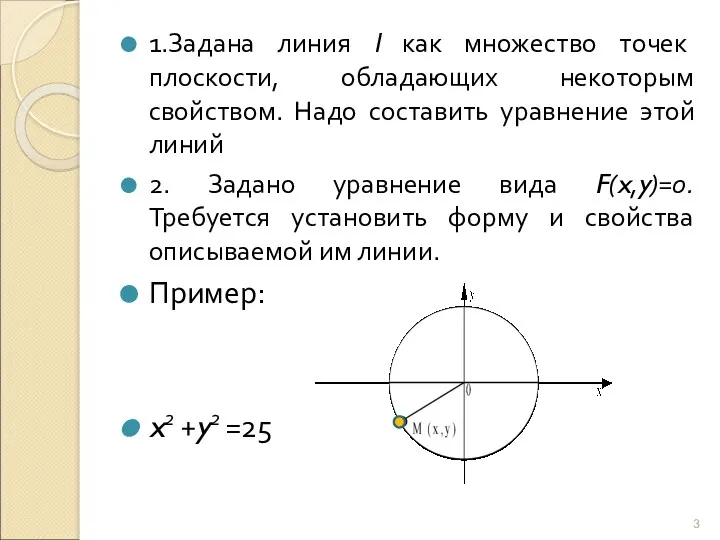
- 3. 1.Задана линия l как множество точек плоскости, обладающих некоторым свойством. Надо составить уравнение этой линий 2.
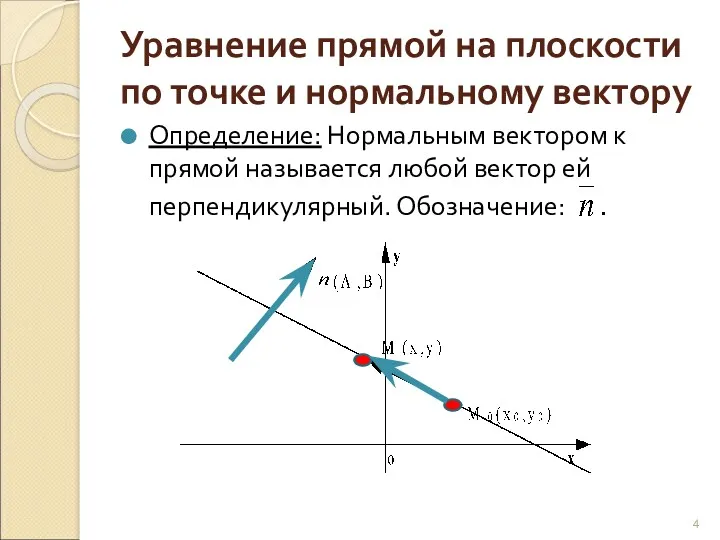
- 4. Уравнение прямой на плоскости по точке и нормальному вектору Определение: Нормальным вектором к прямой называется любой
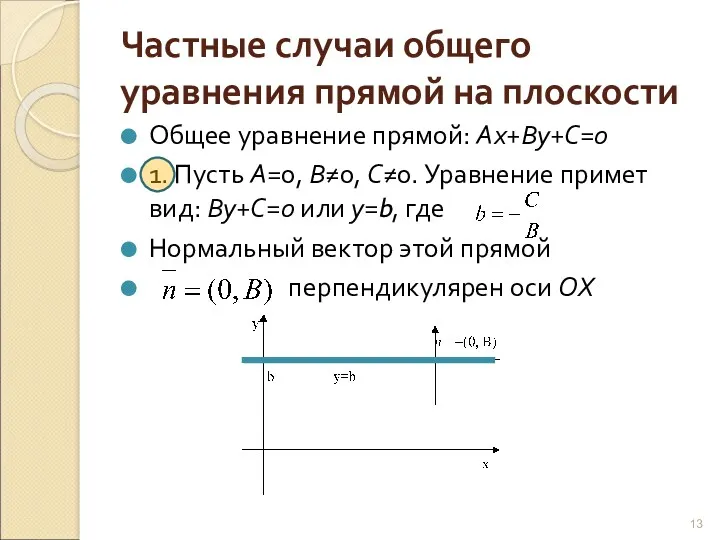
- 5. М0(x0,y0) - точка на прямой, - нормальный вектор этой прямой . (А и В одновременно нулю
- 6. Пример 1. Написать уравнение прямой, проходящей через точку М(1,-3) и имеющую нормальный вектор Решение. Из уравнения
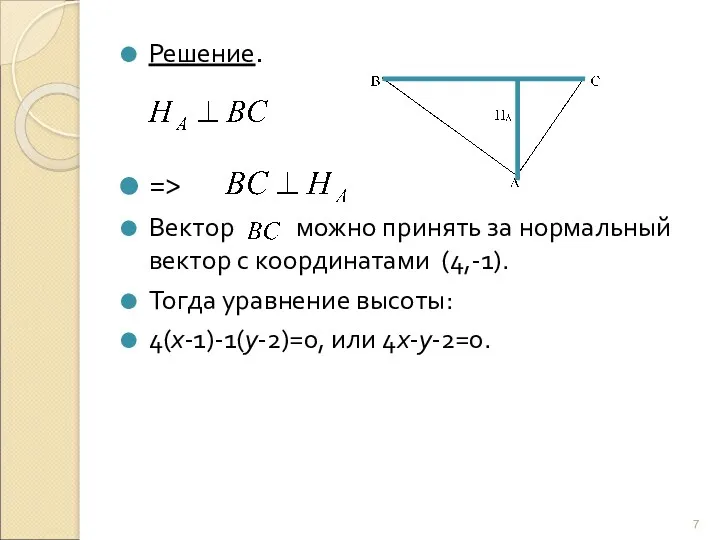
- 7. Решение. => Вектор можно принять за нормальный вектор с координатами (4,-1). Тогда уравнение высоты: 4(х-1)-1(у-2)=0, или
- 8. Пример 3. Написать уравнение прямой, проходящей через точку М(-4,2) и имеющую нормальный вектор . Решение. Из
- 9. Общее уравнение прямой на плоскости На плоскости XOY уравнение Ах+Ву+С=0 определяет прямую линию, при условии, что
- 10. Пример 1. 1. Построить прямую 3х-2у+6=0. 2.Проверить, лежат ли точки М1(1,2) и М2(-4,-3) на этой прямой.
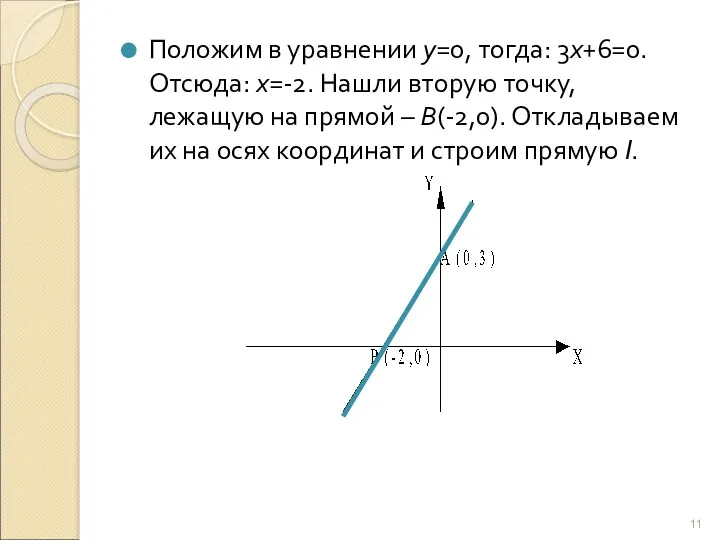
- 11. Положим в уравнении у=0, тогда: 3х+6=0. Отсюда: х=-2. Нашли вторую точку, лежащую на прямой – В(-2,0).
- 12. 2. Проверим, проходит ли прямая через точку М1. Подставим координаты точки в уравнение прямой. Получим: 3·1-2·2+6≠0.
- 13. Частные случаи общего уравнения прямой на плоскости Общее уравнение прямой: Ах+Ву+С=0 1. Пусть А=0, В≠0, С≠0.
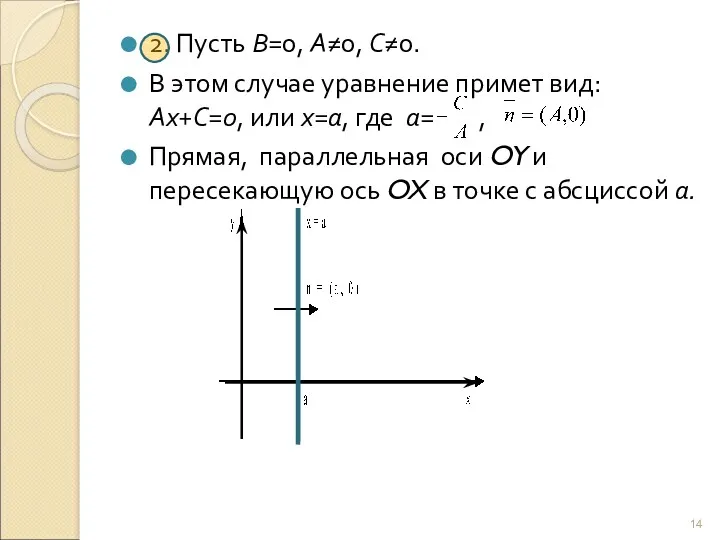
- 14. 2. Пусть В=0, А≠0, С≠0. В этом случае уравнение примет вид: Ах+С=0, или х=а, где а=
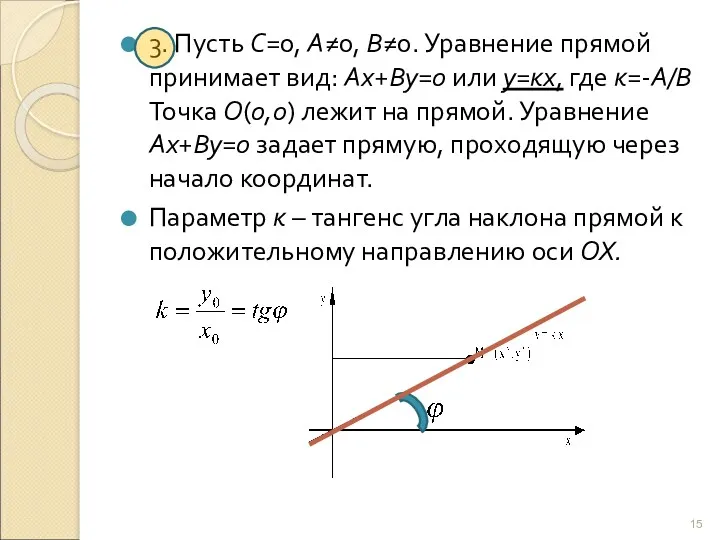
- 15. 3. Пусть С=0, А≠0, В≠0. Уравнение прямой принимает вид: Ах+Ву=0 или у=кх, где к=-А/В Точка О(0,0)
- 16. 4. Пусть А=С=О, В≠О. В этом случае уравнение прямой принимает вид: Ву=0 или у=0. Это уравнение
- 17. Уравнение прямой с угловым коэффициентом Общее уравнение прямой на плоскости: Ах+Ву+С=0. Пусть В≠0, (прямая не параллельна
- 18. Уравнение пучка прямых на плоскости Рассмотрим уравнение : А(х-х0) + В(у-у0) = 0. Пусть В≠0, то
- 19. Пример: Написать уравнение прямой, проходящей через точку М0(3,-1) и образующей с осью ОХ угол 450. Решение:
- 20. Уравнение прямой в отрезках на осях Общее уравнение прямой: Ах+Ву+С=0 или Ах+Ву=-С или
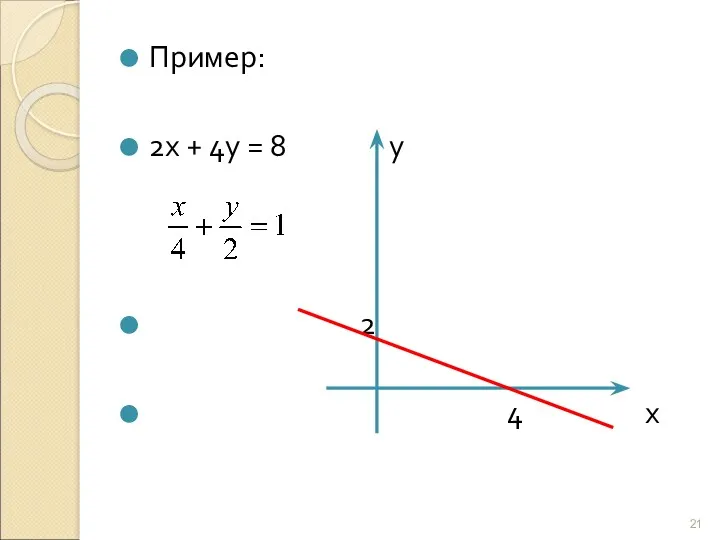
- 21. Пример: 2х + 4у = 8 у 2 4 х
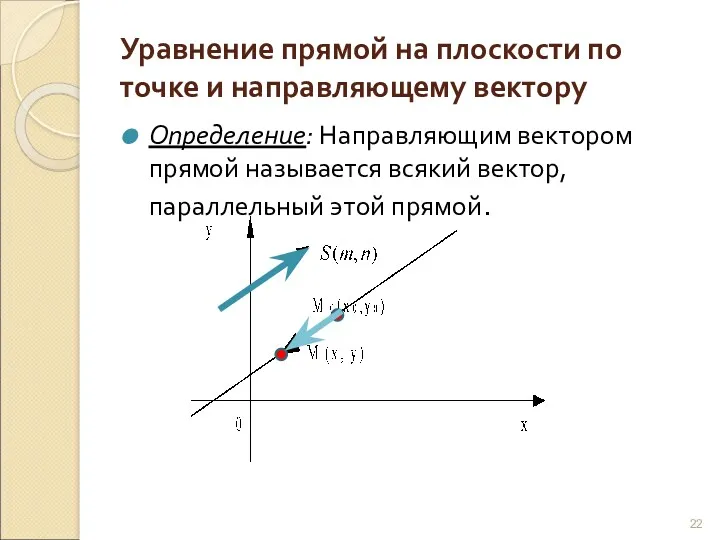
- 22. Уравнение прямой на плоскости по точке и направляющему вектору Определение: Направляющим вектором прямой называется всякий вектор,
- 23. Вектор (х-х0, у-у0) будет параллелен вектору =(m,n). Следовательно, (условие коллинеарности векторов). Это равенство будет справедливо только
- 24. Пример 1: Написать уравнение прямой, проходящей через точку М0(-2,0), параллельно вектору Решение: Из уравнения следует: или
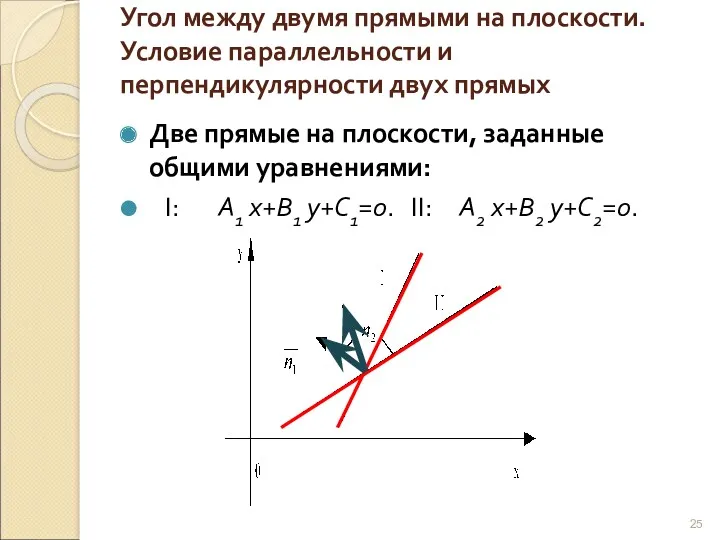
- 25. Угол между двумя прямыми на плоскости. Условие параллельности и перпендикулярности двух прямых Две прямые на плоскости,
- 26. Угол между двумя прямыми равен углу между нормальными векторами этих прямых: и Cos φ= Формула определяет
- 27. Пример 1: Найти угол между прямыми 3х+у-5=0 и 2х-у+1=0. Решение: По формуле имеем: Cosφ= = один
- 28. Пример 2: Найти угол между прямыми 2х+6у+1=0 и 9х-3у+8=0. Решение: По формуле имеем: Cosφ = =O
- 29. Условие параллельности прямых совпадает с условием коллинеарности их нормальных векторов: Условие перпендикулярности прямых совпадает с условием
- 30. Условие параллельности и перпендикулярности прямых, если они заданы уравнениями с угловыми коэффициентами. I: y=k1x+b1 ; II:
- 31. Из условия А1А2 + В1В2=0 => Или Итак, прямые параллельны: к1=к2 Прямые перпендикулярны: угловые коэффициенты обратны
- 32. Пример: Написать уравнение прямой, проходящей через точку М(5, -1) параллельно прямой у=2. Решение: Так как прямые
- 33. Точка пересечения прямых Прямые заданы общими уравнениями: I: А1 х+В1 у+С1=0. II: А2 х+В2 у+С2=0. Пусть
- 35. Скачать презентацию






















 Ознайомлення з дією множення
Ознайомлення з дією множення Тригонометрические уравнения. Задания для устного счета
Тригонометрические уравнения. Задания для устного счета Вариационный ряд
Вариационный ряд Решение квадратных уравнений
Решение квадратных уравнений Введение в теорию графов. Способы представления ориентированных и неориентированных графов
Введение в теорию графов. Способы представления ориентированных и неориентированных графов Презентация: Логические задачи в курсе математики начальной школы
Презентация: Логические задачи в курсе математики начальной школы Метрология. Термины и определения
Метрология. Термины и определения Проект Математика на кухне ЧАСТЬ 1
Проект Математика на кухне ЧАСТЬ 1 Понятие обратной функции. Определение обратных тригонометрических функций
Понятие обратной функции. Определение обратных тригонометрических функций Тренажер. Умножение на 5.
Тренажер. Умножение на 5. Решение заданий С1, С3
Решение заданий С1, С3 Урок математики в 4 классе по теме Письменные способы умножения многозначных чисел
Урок математики в 4 классе по теме Письменные способы умножения многозначных чисел Навантаження і характеристики якості обслуговування викликів
Навантаження і характеристики якості обслуговування викликів Деление обыкновенных дробей. 6 класс
Деление обыкновенных дробей. 6 класс Конечные разности. Первая и вторая интерполяционные формулы Ньютона. Погрешности интерполяции. (Лекция 4)
Конечные разности. Первая и вторая интерполяционные формулы Ньютона. Погрешности интерполяции. (Лекция 4) Пирамиды вокруг нас
Пирамиды вокруг нас Формула площади прямоугольника
Формула площади прямоугольника Проектная работа по математике на тему: Женщины-математики
Проектная работа по математике на тему: Женщины-математики Transactions and database integrity
Transactions and database integrity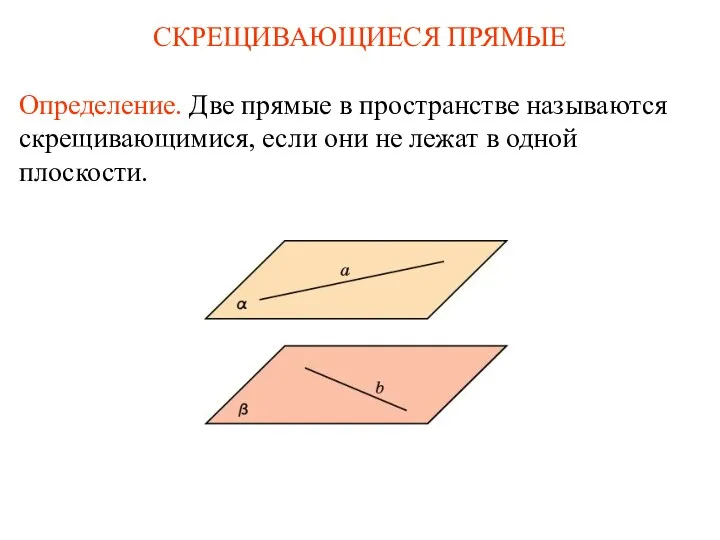 Скрещивающиеся прямые
Скрещивающиеся прямые Урок математики 1 класс по теме Сложение и вычитание в пределах 20 без перехода через десяток УМК Перспектива
Урок математики 1 класс по теме Сложение и вычитание в пределах 20 без перехода через десяток УМК Перспектива Оригами как метод ознакомления детей с формой предметов.
Оригами как метод ознакомления детей с формой предметов. Геометрическая фигура пирамида
Геометрическая фигура пирамида Алгебра логики. Основные понятия
Алгебра логики. Основные понятия Измерения в геометрии
Измерения в геометрии Система подготовки к ОГЭ и ЕГЭ по математике
Система подготовки к ОГЭ и ЕГЭ по математике Модуль геометрия. Подготовка к ОГЭ
Модуль геометрия. Подготовка к ОГЭ Предел последовательности
Предел последовательности