Содержание
- 2. 1854 жылы ағылшын математигі Джордж Буль “Исследование законов мышления” еңбегінде дедуктивтік логика басқаратын әр түрлі ұстанымдар
- 3. Логикалық алгебраның атасы
- 4. Джордж Буль 1815 жылы 2-ші қарашада Англиядағы Линкольн деген жерде дүниеге келген. Ғылыми ортада айналысқандары: математика,
- 5. Бульдік алгебра Буль алгебрасы дегеніміз А және бинарлық операция – конъюнкция («∧») мен дизъюнкциядан («∨»), унарлық
- 6. Бульдік алгебраның анықталуы Буль алгебрасы 0 және 1 элементімен, логикалық операциялармен анықталады. Олар : конъюнкция «∧»
- 7. Аксиомалары:
- 8. Конъюнкция Конъюнкция (латын тілінен байланыс) – логикалық операция, “Және” шылауымен мағыналас, көбейтуді білдіретін аргумент. Негізгі мағынасы:
- 9. Бинарлық конъюнкция
- 10. Дизъюнкция Дизъюнкция – логикалық операция, “Немесе” шылауына жақын мәндес, қосуды білдіретін аргумент. Негізгі мағынасы: барлық жағдайда
- 11. Бинарлық дизъюнкция
- 12. Теріске шығару Теріске шығару – логикалық унарлы операция. “Емес” элементін білдіреді. Негізгі мағынасы: 0 “жалған” элементін
- 13. Теріске шығару
- 14. 1933 жылы американ математигі Хантингтон бульдік алгебра үшін келесі жүйелерді ұсынды: 1)Коммутативтілік аксиомасы: x+y=y+x 2)Ассоциативтілік аксиомасы:
- 16. Бульдік алгебра Екілік санау жүйе сі процессор
- 17. Қорытынды Буль алгебрасы – бүгінгі күн есептеу техникасының негізі. Оның негізгі құрылымдық элементтері мен операциялары “Ақиқат”
- 18. Қолданылған әдебиеттер:
- 20. Скачать презентацию















 Презентация-тренажёр по таблице умножения
Презентация-тренажёр по таблице умножения Методическая разработка (презентация) Дидактические игры и упражнения занимательного характера в ГПД.
Методическая разработка (презентация) Дидактические игры и упражнения занимательного характера в ГПД. Определённый интеграл
Определённый интеграл Презентация по математике Секунда. УМК Перспектива, 4 класс
Презентация по математике Секунда. УМК Перспектива, 4 класс презентация к уроку математики по теме Увеличение и уменьшение числа в 10, 100, 1000 раз
презентация к уроку математики по теме Увеличение и уменьшение числа в 10, 100, 1000 раз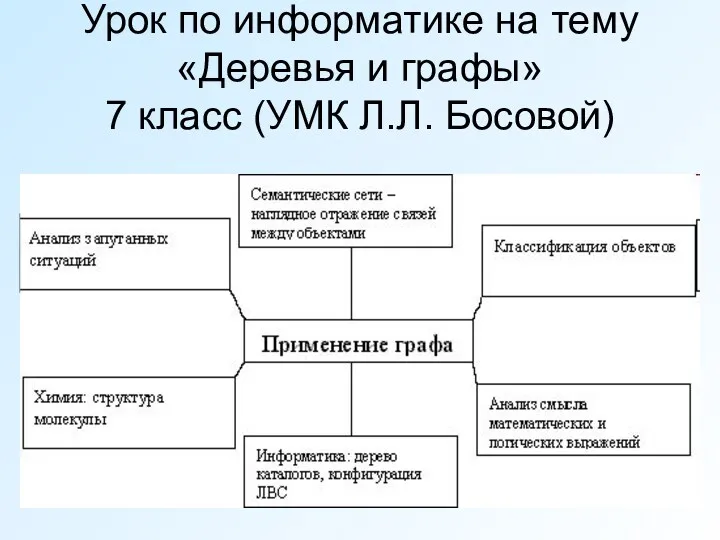 Деревья и графы
Деревья и графы Простые и составные числа
Простые и составные числа Цифра и число 4
Цифра и число 4 Розв’язання систем лінійних алгебраїчних рівнянь
Розв’язання систем лінійних алгебраїчних рівнянь Отношением отрезков AB и CD называется отношение их длин
Отношением отрезков AB и CD называется отношение их длин Маленькая принцесса
Маленькая принцесса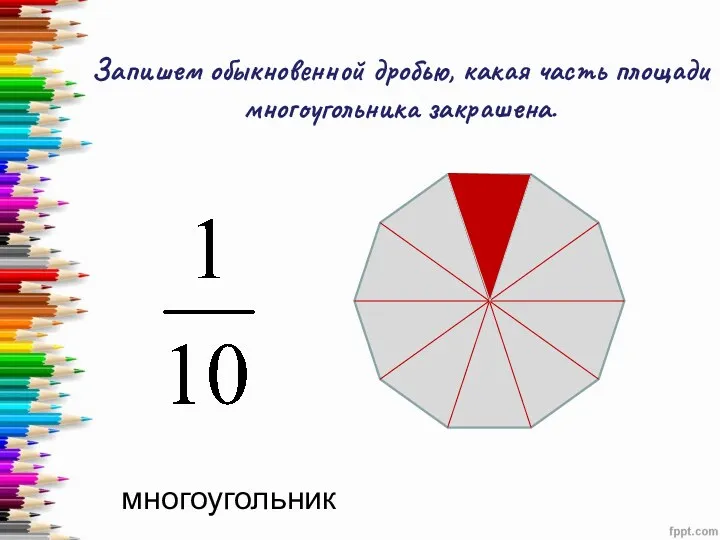 Дробные числа. Запись обыкновенной дроби
Дробные числа. Запись обыкновенной дроби Деление с остатком
Деление с остатком Розв’язування прямокутних трикутників
Розв’язування прямокутних трикутників Тест по теме: Параллельность в пространстве
Тест по теме: Параллельность в пространстве Подготовка к ЕГЭ по математике. Решение задач В12
Подготовка к ЕГЭ по математике. Решение задач В12 Системы неравенств с двумя переменными
Системы неравенств с двумя переменными Общие сведения об измерениях, средствах измерений и их метрологических характеристиках
Общие сведения об измерениях, средствах измерений и их метрологических характеристиках Центральный и вписанные углы
Центральный и вписанные углы Сравнение смешанных чисел
Сравнение смешанных чисел презентация к уроку математики на тему Алгоритм письменного деления. Прикидка результата.Сравнение выражений.
презентация к уроку математики на тему Алгоритм письменного деления. Прикидка результата.Сравнение выражений. Теорема синусов
Теорема синусов Урок математики. 3 класс. Чтение и запись многозначных чисел. Закрепление изученного.
Урок математики. 3 класс. Чтение и запись многозначных чисел. Закрепление изученного. Показательная функция. Решение показательных уравнений и неравенств в рамках подготовки к ЕГЭ
Показательная функция. Решение показательных уравнений и неравенств в рамках подготовки к ЕГЭ Урок математики 1 класс. Повторение числа от 1 до 10.
Урок математики 1 класс. Повторение числа от 1 до 10. Математика в химии
Математика в химии Математическое кафе. Открытый урок по математике в 5 классе
Математическое кафе. Открытый урок по математике в 5 классе Термины технологического прогнозирования
Термины технологического прогнозирования