Содержание
- 2. Понятия теории графов Граф - некоторое конечное множество V точек на плоскости и конечный набор линий
- 3. Понятия теории графов Омск Новосибирск Павлодар Красноярск 650 420 590 800 А В С D 1500
- 4. Понятия теории графов Степень вершин: deg A=deg D=2, deg C=deg B=3. Изолированная вершина deg V=0, концевая
- 5. Понятия теории графов Мультиграф Псевдограф Неориентиро- ванный граф Ориентиро- ванный граф
- 6. Пример графа Охарактеризовать граф, Перечислить вершины, смежные вершины, изолированные вершины, Назвать ребра, петли, дуги Составить матрицу
- 7. Характерные свойства графов 1. Сумма степеней вершин графа равна удвоенному числу его ребер 2. В любом
- 8. Изоморфизм графов 4 графа одного порядка, с одинаковым числом ребер, Сравнить смежные вершины
- 9. Способы задания графов: Графический. Все элементы множества V обозначаются точками на плоскости, проводятся линии, соединяющие вершины.
- 11. Скачать презентацию

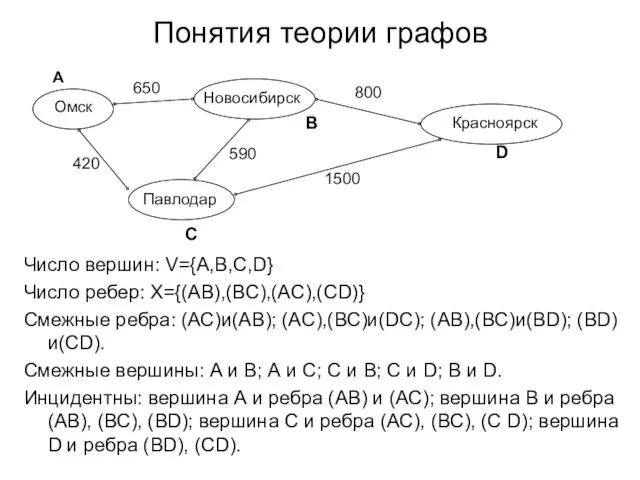
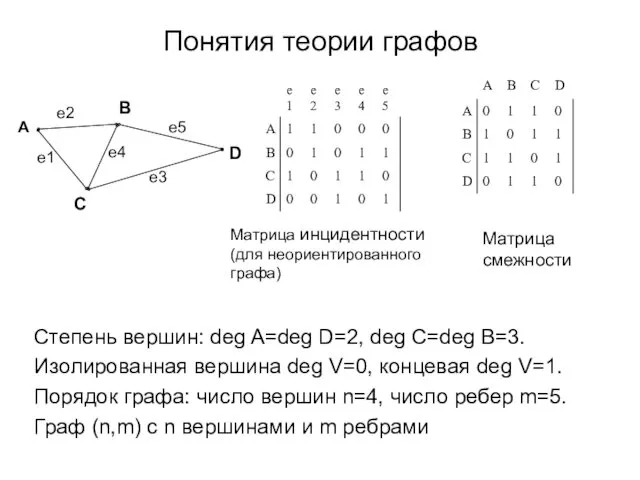
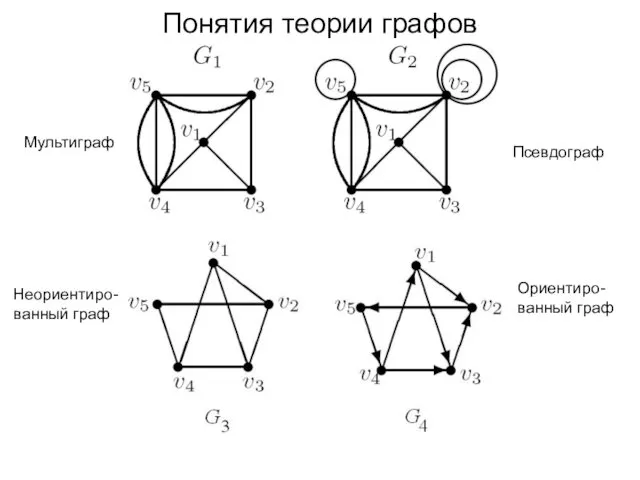
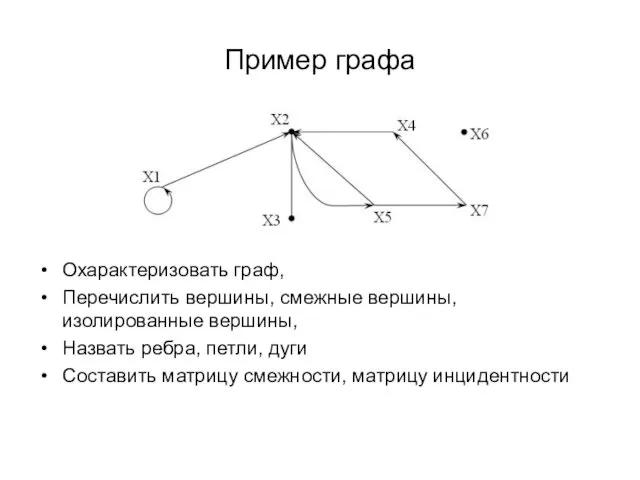

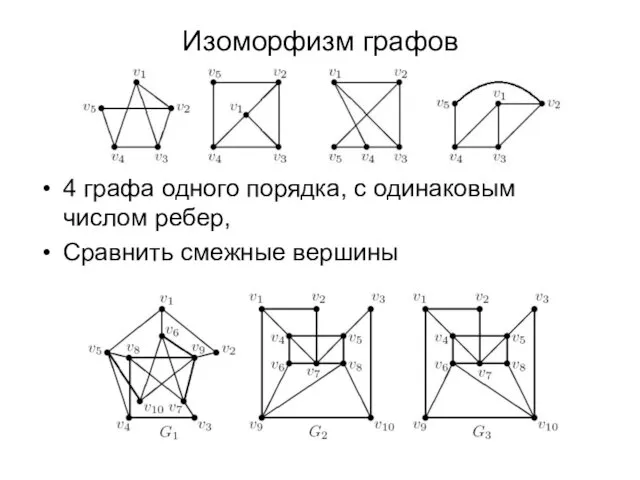

 Таблица сложения
Таблица сложения Круговые диаграммы
Круговые диаграммы Векторы в пространстве
Векторы в пространстве Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Закрепление навыков решения квадратных уравнений. Формирование у учащихся умения решать биквадратные уравнения. 8 класс
Закрепление навыков решения квадратных уравнений. Формирование у учащихся умения решать биквадратные уравнения. 8 класс Решение простейших тригонометрических уравнений. 10 класс
Решение простейших тригонометрических уравнений. 10 класс Дифференциальные уравнения и ряды. Применение рядов Тейлора. Периодические функции. Ряды Фурье
Дифференциальные уравнения и ряды. Применение рядов Тейлора. Периодические функции. Ряды Фурье Обыкновенные дроби
Обыкновенные дроби Линейная функция у = kx + b, её график и свойства
Линейная функция у = kx + b, её график и свойства Тест по теме: Взаимное расположение прямых в пространстве. Параллельность прямых, прямой и плоскости
Тест по теме: Взаимное расположение прямых в пространстве. Параллельность прямых, прямой и плоскости урок математики в 3 классе Нахождение доли числа
урок математики в 3 классе Нахождение доли числа Числа 1, 2, 3. Знаки +, -, =
Числа 1, 2, 3. Знаки +, -, = Презентация по математике по теме Вычислительный приём вида 35-7.
Презентация по математике по теме Вычислительный приём вида 35-7. Великие математические умы
Великие математические умы Урок математики в 1 классе Сложение и вычитание длин отрезков
Урок математики в 1 классе Сложение и вычитание длин отрезков Прямоугольный параллелепипед
Прямоугольный параллелепипед Урок математики Арифметические действия над числами
Урок математики Арифметические действия над числами Неделя математики, физики, информатики
Неделя математики, физики, информатики Знаки и символы в математике и русском языке
Знаки и символы в математике и русском языке Понятие арифметического квадратного корня
Понятие арифметического квадратного корня Косий згин. Лекція 9
Косий згин. Лекція 9 Английский математик Август де Морган
Английский математик Август де Морган Математика в профессии статистика
Математика в профессии статистика Линейная алгебра. Матрицы
Линейная алгебра. Матрицы Производная и ее применение
Производная и ее применение Невский проспект Санкт-Петербурга в цифрах. Публичная библиотека в Санкт-Петербурге (часть 6)
Невский проспект Санкт-Петербурга в цифрах. Публичная библиотека в Санкт-Петербурге (часть 6) Число 9. Цифра 9. Урок с использованием ИКТ
Число 9. Цифра 9. Урок с использованием ИКТ Математическая игра Цифра семь известна всем
Математическая игра Цифра семь известна всем