Слайд 2

Преподаватель
Дмитрий
Игоревич
Балашов
Слайд 3

Дисциплина состоит из 6 модулей:
Численное решение нелинейных уравнений.
Численное решение СЛАУ.
Численное решение
СНУ.
Численное интегрирование.
Интерполяция и аппроксимация функций.
Численное решение ОДУ.
Форма отчетности – ЗАЧЕТ
Слайд 4

Численное решение
нелинейных уравнений
Слайд 5

Общий вид нелинейного уравнения
f(x)=0
где
x – аргумент,
f(x) – функционал
одной переменной
Слайд 6

Существуют различные методы решения нелинейных уравнений
Наиболее распространенный:
аналитический метод
Слайд 7

Трансцендентные уравнения
Пример:
Или после преобразования:
Слайд 8
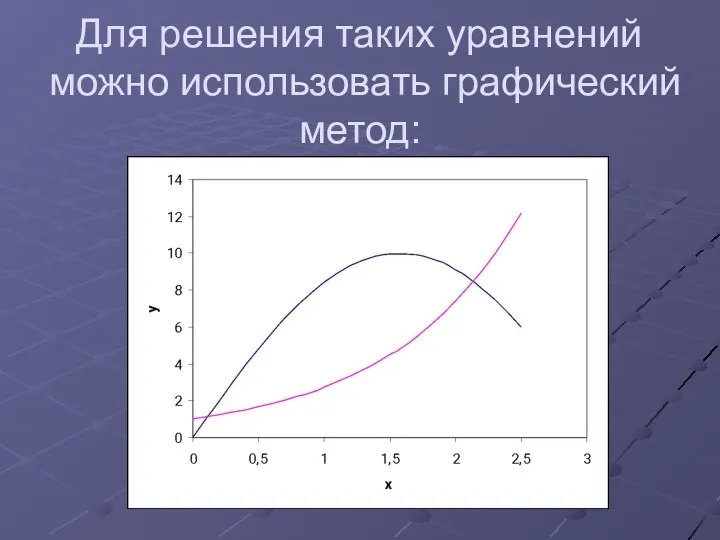
Для решения таких уравнений можно использовать графический метод:
Слайд 9

Недостаток графического метода:
Низкая точность получаемого результата.
Также для решения подобного рода уравнений
можно использовать численные методы
Слайд 10

Теорема
о существовании корней уравнения f(x)=0
Если на концах интервала [a, b] функция
f(x) имеет разные знаки, то это значит, что в интервале [a, b] уравнение f(x)=0 имеет хотя бы один корень.
Слайд 11
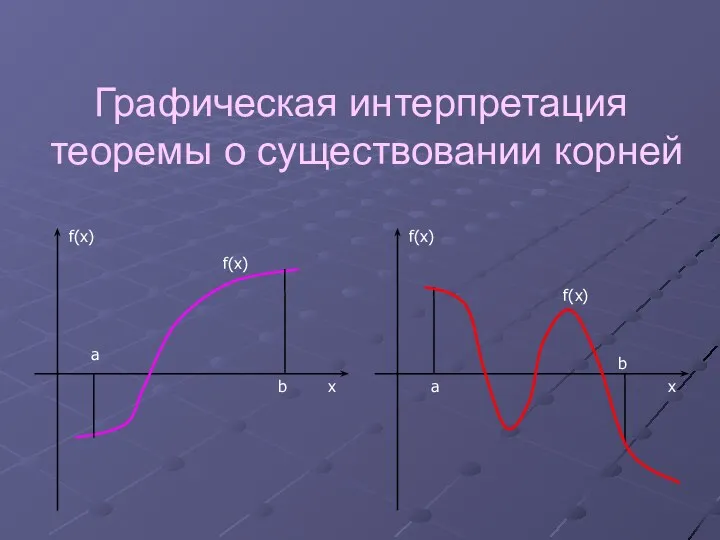
Графическая интерпретация теоремы о существовании корней
Слайд 12
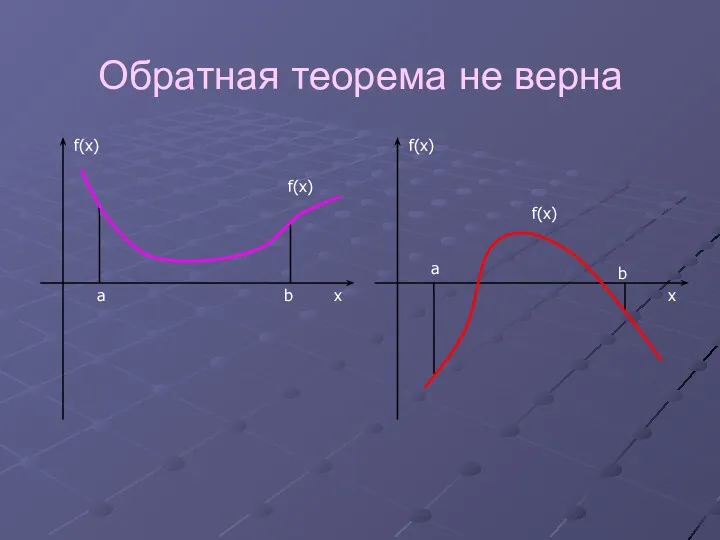
Обратная теорема не верна
Слайд 13

Большинство численных методов основаны на этой теореме
В дальнейшем примем допущение о
том, что на интервале [a, b] имеется только один корень уравнения f(x)=0
Слайд 14
![Метод половинного деления (метод дихотомии, метод бисекции) Исходные данные для реализации метода: f(x)=0 [a, b] E](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/314387/slide-13.jpg)
Метод половинного деления
(метод дихотомии,
метод бисекции)
Исходные данные для реализации метода:
f(x)=0
[a, b]
E
Слайд 15

Алгоритм метода:
Отрезок ab делится пополам точкой с.
Рассчитываются значения функции f(x) в
точках a, b и c.
Один из отрезков ac или cb, на концах которого функция f(x) имеет одинаковые знаки, отбрасывают и далее продолжают работать с оставшимся отрезком.
Процесс повторяется до тех пор, пока длина оставшегося отрезка не станет меньше величины точности Е.
|a-b|В этом случае за корень уравнения можно принять середину полученного отрезка
x=(a+b)/2
Слайд 16
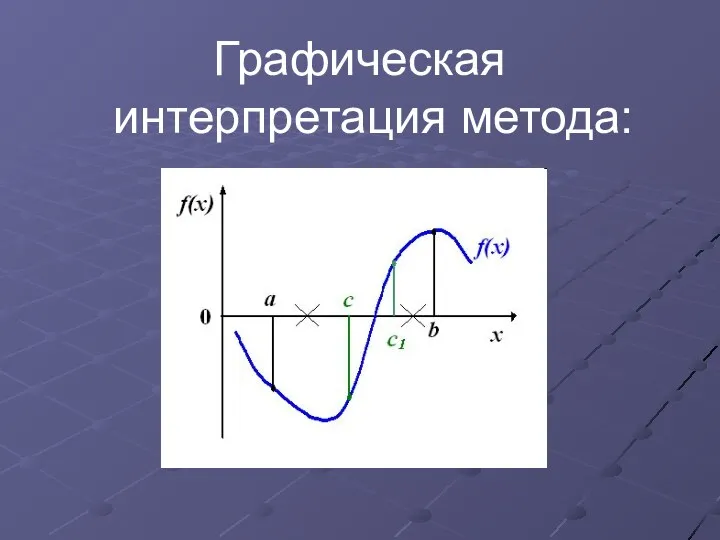
Графическая интерпретация метода:
Слайд 17
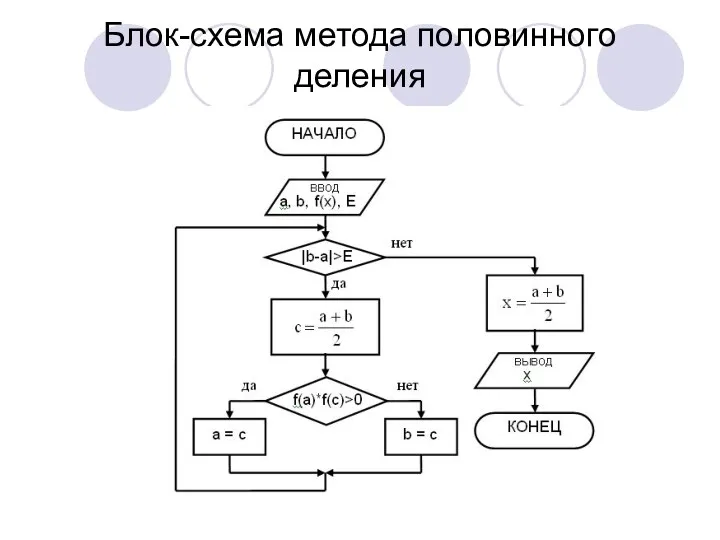
Блок-схема метода половинного деления
Слайд 18

ДОСТОИНСТВА метода
Простота метода
Устойчивость метода
НЕДОСТАТОК метода
Низкая скорость сходимости
Слайд 19
![Метод хорд Исходные данные для реализации метода: f(x)=0 [a, b] E](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/314387/slide-18.jpg)
Метод хорд
Исходные данные для реализации метода:
f(x)=0
[a, b]
E
Слайд 20

Алгоритм метода:
Отрезок ab делится на 2 отрезка точкой с. Точка с
является точкой пересечения оси абсцисс ОХ с хордой, соединяющей точки f(a) и f(b).
Рассчитываются значения функции f(x) в точках
a, b и c.
Один из отрезков ac или cb, на концах которого функция f(x) имеет одинаковые знаки, отбрасывается и далее продолжают работать с оставшимся отрезком.
Процесс повторяется до тех пор, пока длина оставшегося отрезка не станет меньше величины точности Е.
|a-b|В этом случае за корень уравнения можно принять середину полученного отрезка
x=(a+b)/2
Слайд 21
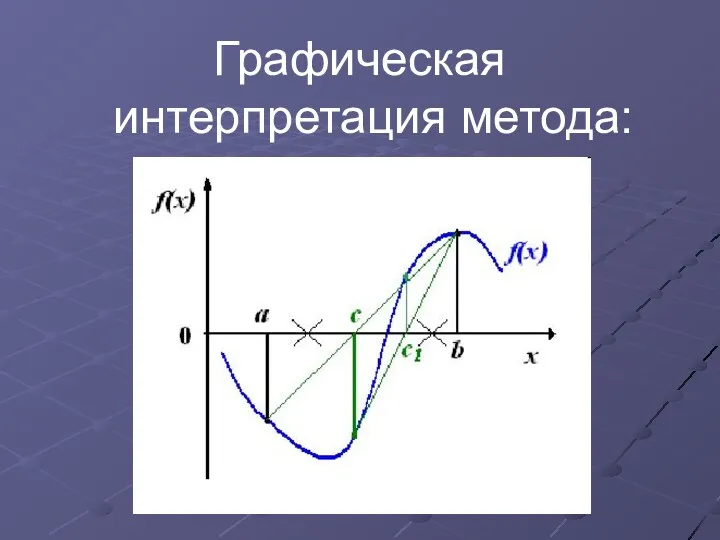
Графическая интерпретация метода:
Слайд 22
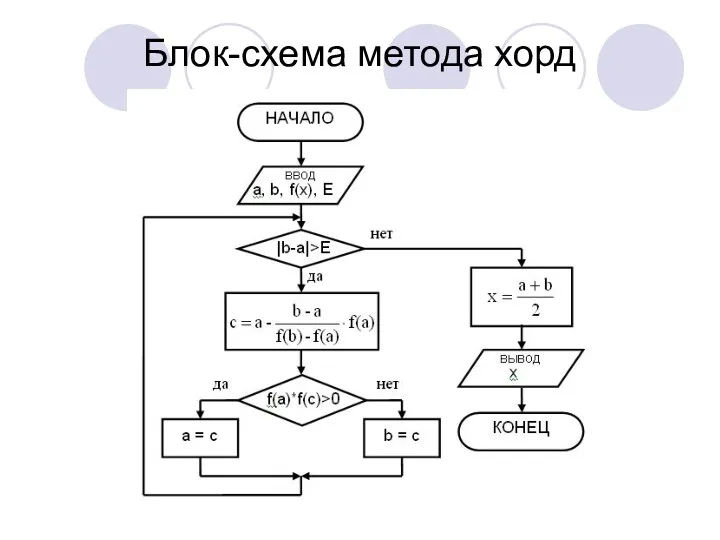
Слайд 23

ДОСТОИНСТВА метода
Простота метода
Устойчивость метода
Более высокая скорость сходимости
НЕДОСТАТОК метода
Для некоторых частных случаев
метод не применим
Слайд 24

Метод касательных
(метод Ньютона)
Исходные данные для реализации метода:
f(x)=0
f ’(x)
x0
E
Слайд 25

Алгоритм метода:
В точке x0 к графику функции f(x) проводится касательная.
Находится
более точное значение x – это точка пересечения касательной с осью абсцисс ОХ.
Таким образом каждая последующая точка будет лежать ближе к истинному решению, чем предыдущая.
Последующая точка рассчитывается через предыдущую по формуле
xi+1=xi-f(xi)/f ’(xi)
Процесс повторяется до тех пор, пока разность между последующей и предыдущей точкой не станет меньше величины точности Е
|xi+1-xi|В этом случае за корень уравнения можно принять последнюю найденную точку xi.
Слайд 26
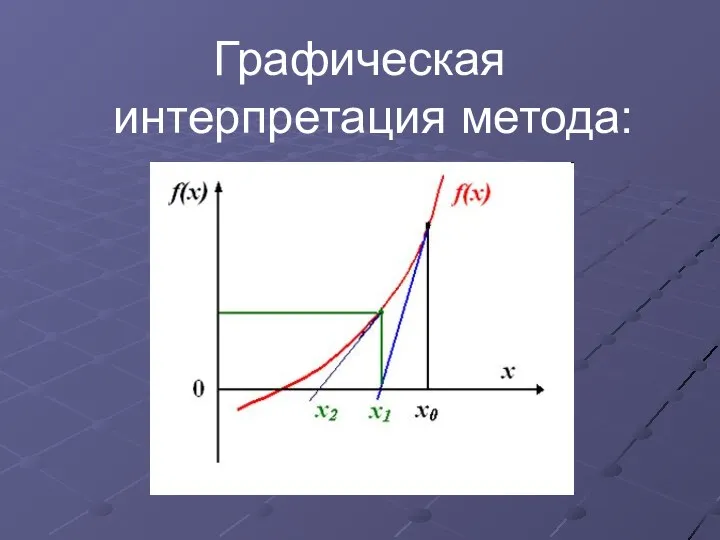
Графическая интерпретация метода:
Слайд 27
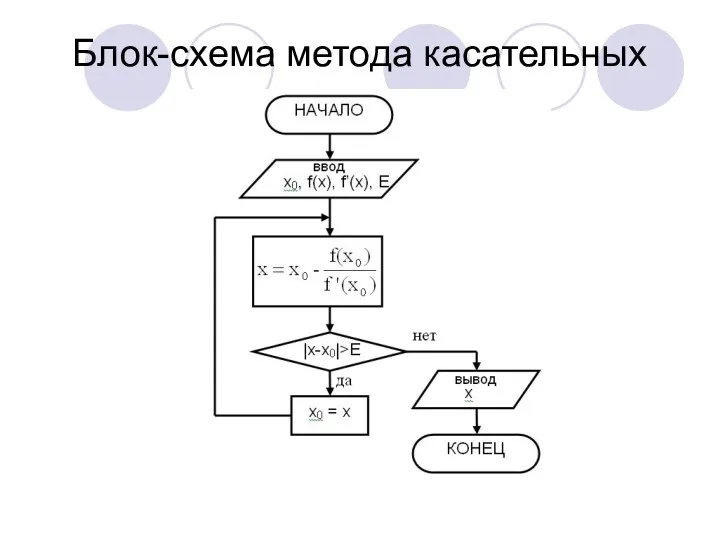
Блок-схема метода касательных
Слайд 28

ДОСТОИНСТВО метода
Высокая скорость сходимости
НЕДОСТАТКИ метода
Необходимость задавать производную функции в аналитическом виде
Метод
является неустойчивым
Слайд 29

Метод секущих
Метод секущих является модификацией метода касательных
Исходные данные для реализации метода:
f(x)
x0
E
Слайд 30

Алгоритм метода:
Алгоритм аналогичен предыдущему методу, но производная функции вычисляется по приближенной
формуле:
где Δx – малая величина. Как правило за эту величину принимают величину точности Е:












![Метод половинного деления (метод дихотомии, метод бисекции) Исходные данные для реализации метода: f(x)=0 [a, b] E](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/314387/slide-13.jpg)




![Метод хорд Исходные данные для реализации метода: f(x)=0 [a, b] E](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/314387/slide-18.jpg)











 Умножение многочлена на многочлен
Умножение многочлена на многочлен Числа 91 – 100. Сотня. Задача на знаходження невідомого доданка. Урок №98
Числа 91 – 100. Сотня. Задача на знаходження невідомого доданка. Урок №98 Объём фигуры. Единицы объёма
Объём фигуры. Единицы объёма Ділення двоцифрового числа на одноцифрове виду 39:3
Ділення двоцифрового числа на одноцифрове виду 39:3 Математический ринг
Математический ринг Формирование умений школьников использовать приобретенные знания в практической деятельности
Формирование умений школьников использовать приобретенные знания в практической деятельности Точки перегиба функции, выпуклость графика функции. Исследование функции на выпуклость
Точки перегиба функции, выпуклость графика функции. Исследование функции на выпуклость Презентация к уроку математики в 1 классе
Презентация к уроку математики в 1 классе Незнайкины задачки (1 класс)
Незнайкины задачки (1 класс) Правильные многогранники в природе
Правильные многогранники в природе Презентация к уроку математики в 1 классе. Числа от 1 до 20.
Презентация к уроку математики в 1 классе. Числа от 1 до 20. Вычитание двузначных чисел
Вычитание двузначных чисел Симметрия на координатной плоскости. 6 класс
Симметрия на координатной плоскости. 6 класс Развитие памяти, внимания и мышления на занятиях по математике
Развитие памяти, внимания и мышления на занятиях по математике Тригонометрические формулы
Тригонометрические формулы Решение неравенств методом интервалов. 9 класс
Решение неравенств методом интервалов. 9 класс Алгебраическая задача на неравенства. Занимательная математика – 5 класс
Алгебраическая задача на неравенства. Занимательная математика – 5 класс Сравнение, сложение и вычитание дробей с разными знаменателями. 6 класс
Сравнение, сложение и вычитание дробей с разными знаменателями. 6 класс Презентация: Логические задачи в курсе математики начальной школы
Презентация: Логические задачи в курсе математики начальной школы Презентация к уроку математики во 2 классе
Презентация к уроку математики во 2 классе Формирование познавательных учебных действий на уроках математики
Формирование познавательных учебных действий на уроках математики Распределительное свойство умножения. 6 класс
Распределительное свойство умножения. 6 класс Математика в живописи
Математика в живописи Презентация к диплому Обучение детей старшего дошкольного возраста пространственному моделированию в процессе игр и игровых упражнений
Презентация к диплому Обучение детей старшего дошкольного возраста пространственному моделированию в процессе игр и игровых упражнений Способы сложения
Способы сложения Готовимся решать задачи
Готовимся решать задачи Обчислення на основі нумерації. Знаходження невідомого доданка. Складання задачі за числовими даними. Урок №112
Обчислення на основі нумерації. Знаходження невідомого доданка. Складання задачі за числовими даними. Урок №112 Угол прямой и развернутый. Чертежный треугольник
Угол прямой и развернутый. Чертежный треугольник