Содержание
- 2. Основные понятия теории числовых рядов 1. Основные определения Пусть задана числовая последовательность {un} ОПРЕДЕЛЕНИЕ. Выражение вида
- 3. Если начиная с некоторого номера N для членов ряда справедливо равенство uN = uN + 1
- 4. Для ряда ∑un запишем последовательность S1 = u1 , S2 = u1 + u2 , …
- 5. ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ РЯДОВ 1) Рассматривается в математическом анализе: Определить, сходится или расходится заданный ряд (говорят:
- 10. 2. Основные свойства числовых рядов ТЕОРЕМА 1. Поведение ряда относительно сходимости не изменится, если добавить (отбросить)
- 11. ТЕОРЕМА 2 (об арифметических действиях над сходящимися рядами) Если ряд ∑un сходится и его сумма равна
- 12. ТЕОРЕМА 3 (необходимый признак сходимости ряда). Если ряд ∑un сходится, то СЛЕДСТВИЕ теоремы 3 (достаточное условие
- 15. Сходимость знакоположительных рядов ЛЕММА (необходимое и достаточное условие сходимости знакоположительного ряда). Знакоположительный ряд сходится ⇔ последовательность
- 16. ТЕОРЕМА (второй признак сравнения). Пусть ∑un и ∑vn – знакоположительные ряды. Если при n → ∞
- 17. ЭТАЛОННЫЕ РЯДЫ, которые используются в признаках сравнения: а) гармонический ряд – расходится; б) обобщенный гармонический ряд
- 20. ТЕОРЕМА (признак Даламбера). Пусть ∑un – знакоположительный ряд и существует Тогда а) если ℓ б) если
- 23. ТЕОРЕМА (признак Коши). Пусть ∑un – знакоположительный ряд и существует Тогда а) если ℓ б) если
- 25. ТЕОРЕМА (интегральный признак Коши). Пусть ∑un – знакоположительный ряд, f(x) – непрерывная, неотрицательная, монотонно убывающая на
- 28. Сходимость знакопеременных рядов 1. Знакочередующиеся ряды ОПРЕДЕЛЕНИЕ. Ряд, у которого любые рядом стоящие члены имеют противоположные
- 29. ТЕОРЕМА (признак сходимости Лейбница). Пусть знакочередующийся ряд ∑(–1)n + 1 ⋅ un удовлетворяет условиям: 1) члены
- 31. Замечания. 1) Ряд ∑(–1)n + 1 ⋅ un будет сходиться и в том случае, когда условие
- 32. 2. Абсолютная и условная сходимость знакопеременных рядов Пусть ∑un – знакопеременный ряд. Рассмотрим ряд ∑| un
- 34. СВОЙСТВА АБСОЛЮТНО И УСЛОВНО СХОДЯЩИХСЯ РЯДОВ 1) ТЕОРЕМА. Если ряды ∑un и ∑vn сходятся абсолютно, то
- 35. 2) ТЕОРЕМА (о перестановке членов ряда). а) Если ряд ∑un сходится абсолютно, то ряд, полученный из
- 36. ТЕОРЕМА (о сходимости произведения рядов). Пусть ряды ∑un и ∑vn сходятся абсолютно и их суммы равны
- 38. Скачать презентацию



































 Сравнение и измерение отрезков. 7 класс
Сравнение и измерение отрезков. 7 класс История космонавтики в цифрах
История космонавтики в цифрах Тренажер Нумерация чисел в пределах 100 2 класс
Тренажер Нумерация чисел в пределах 100 2 класс Нахождение числа по его процентам
Нахождение числа по его процентам Абсолютные и относительные показатели. Статистика, тема 6
Абсолютные и относительные показатели. Статистика, тема 6 Обобщение и систематизация знаний по теме десятичные дроби
Обобщение и систематизация знаний по теме десятичные дроби Древние системы счисления в современном мире
Древние системы счисления в современном мире Задачі на визначення, на скільки коротший. Обчислення значень виразів
Задачі на визначення, на скільки коротший. Обчислення значень виразів Презентация к уроку математики Целое и часть Диск
Презентация к уроку математики Целое и часть Диск Теория поверхностей. Касательная плоскость поверхности. Нормаль
Теория поверхностей. Касательная плоскость поверхности. Нормаль Задачи по математике
Задачи по математике Умножение и деление обыкновенной дроби на натуральное число
Умножение и деление обыкновенной дроби на натуральное число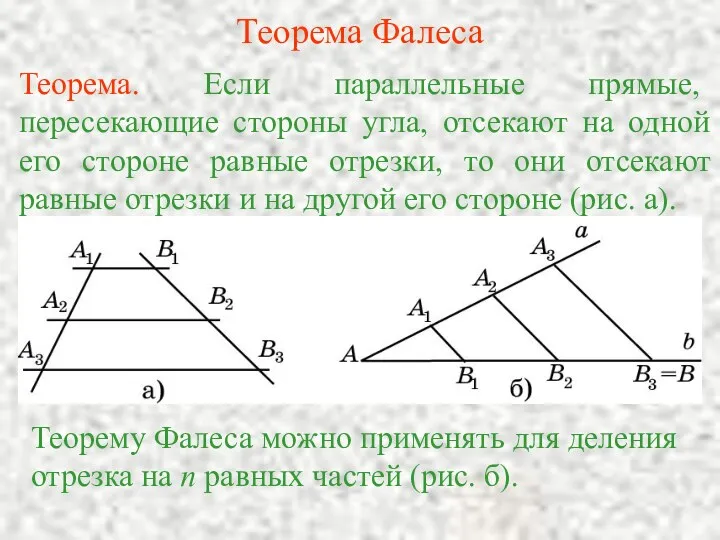 Теорема Фалеса
Теорема Фалеса Переместительное свойство умножения
Переместительное свойство умножения Производная функции в точке
Производная функции в точке Графическая работа. Следствия из аксиом стереометрии
Графическая работа. Следствия из аксиом стереометрии Интеллектуальная игра Великие математики
Интеллектуальная игра Великие математики Презентация к уроку математики Проверка деления с остатком и обобщение знаний об историческом летосчислении
Презентация к уроку математики Проверка деления с остатком и обобщение знаний об историческом летосчислении Презентация к уроку о Великой Отечественной войне
Презентация к уроку о Великой Отечественной войне Предикаты и формулы. Интерпретации. Истинность и выполнимость формул. Нормальные формы. (Лекция 3-4)
Предикаты и формулы. Интерпретации. Истинность и выполнимость формул. Нормальные формы. (Лекция 3-4) Задачи на нахождение дроби от числа и числа по его части. Математика. 5 класс
Задачи на нахождение дроби от числа и числа по его части. Математика. 5 класс интерактивный тренажёр Вычитание в пределах 20
интерактивный тренажёр Вычитание в пределах 20 Презентация к интегрированному уроку Математика и окружающий мир.
Презентация к интегрированному уроку Математика и окружающий мир. Математика о вреде курения. 6 класс
Математика о вреде курения. 6 класс Игра-тренажёр На стройке. 1 класс
Игра-тренажёр На стройке. 1 класс Готовимся к ЕГЭ. Задача С2. Задачи, где присутствует построение сечения
Готовимся к ЕГЭ. Задача С2. Задачи, где присутствует построение сечения Теорема Пифагора и неизвестные способы ее доказательства
Теорема Пифагора и неизвестные способы ее доказательства Трикутники. Види трикутників. Казка (математика 5 клас)
Трикутники. Види трикутників. Казка (математика 5 клас)