Содержание
- 2. Производная функции в точке Пусть функция f (x) определена в некоторой окрестности точки х0. Производной функции
- 3. Определение 2: Автор: И. В. Дайняк, к.т.н., доцент кафедры высшей математики БГУИР Производную функции y =
- 4. Односторонние производные функции в точке Правая производная: Если функция f (x) определена в некоторой правой полуокрестности
- 5. Пример 1: Найти производную функции Автор: И. В. Дайняк, к.т.н., доцент кафедры высшей математики БГУИР в
- 6. Теорема: Если функция f (x) имеет производную в точке x0, то она непрерывна в точке x0.
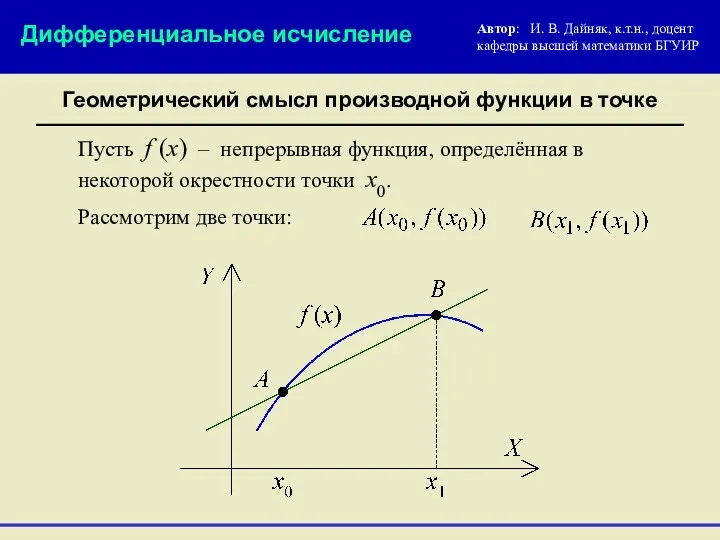
- 7. Геометрический смысл производной функции в точке Автор: И. В. Дайняк, к.т.н., доцент кафедры высшей математики БГУИР
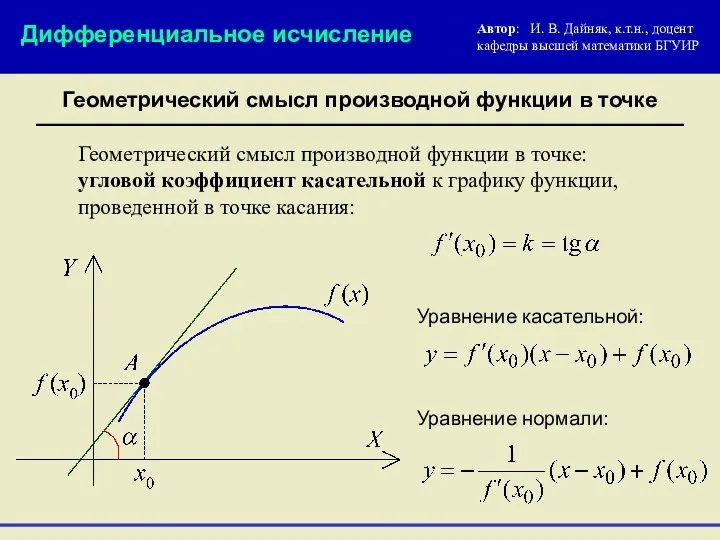
- 8. Геометрический смысл производной функции в точке Автор: И. В. Дайняк, к.т.н., доцент кафедры высшей математики БГУИР
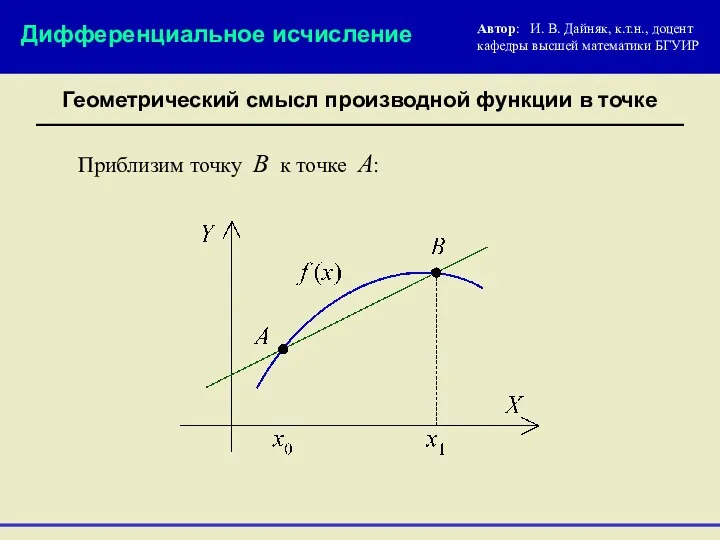
- 9. Геометрический смысл производной функции в точке Автор: И. В. Дайняк, к.т.н., доцент кафедры высшей математики БГУИР
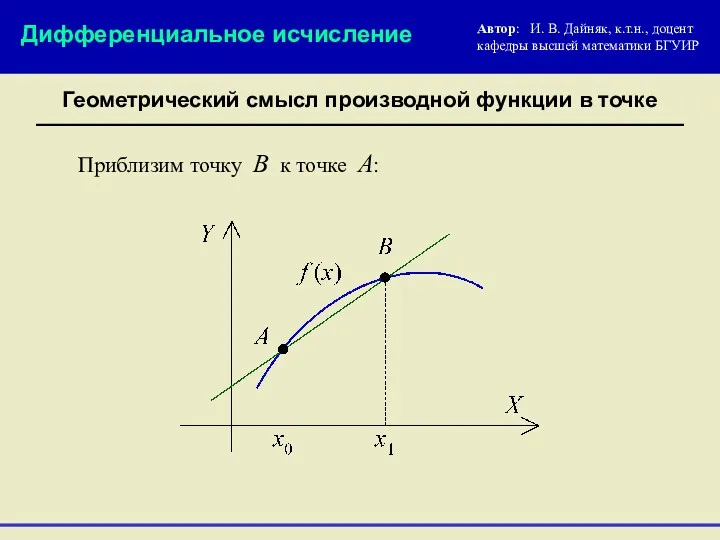
- 10. Геометрический смысл производной функции в точке Автор: И. В. Дайняк, к.т.н., доцент кафедры высшей математики БГУИР
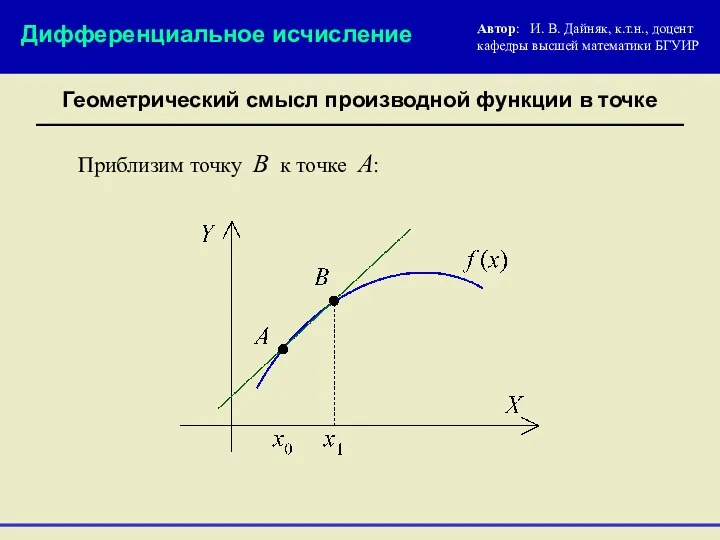
- 11. Геометрический смысл производной функции в точке Автор: И. В. Дайняк, к.т.н., доцент кафедры высшей математики БГУИР
- 12. Геометрический смысл производной функции в точке Автор: И. В. Дайняк, к.т.н., доцент кафедры высшей математики БГУИР
- 13. Физический смысл производной функции в точке Автор: И. В. Дайняк, к.т.н., доцент кафедры высшей математики БГУИР
- 14. Физический смысл производной функции в точке Автор: И. В. Дайняк, к.т.н., доцент кафедры высшей математики БГУИР
- 15. Теорема 1: Основные формулы дифференцирования Пусть функции u = u(x) и v = v(x) имеют производную
- 16. Теорема 1: Основные формулы дифференцирования Автор: И. В. Дайняк, к.т.н., доцент кафедры высшей математики БГУИР Дифференциальное
- 17. Теорема 2: Дифференцирование сложной функции Пусть функция g(x) имеет производную в точке x0, а функция f
- 18. Если функция f (x) имеет производную в любой точке некоторого интервала [a, b], то её производная
- 19. 1. Постоянная функция f (x) = c, где с – константа. Автор: И. В. Дайняк, к.т.н.,
- 20. 2. Показательная функция Автор: И. В. Дайняк, к.т.н., доцент кафедры высшей математики БГУИР Дифференциальное исчисление Производные
- 21. 3. Степенная функция Автор: И. В. Дайняк, к.т.н., доцент кафедры высшей математики БГУИР Дифференциальное исчисление Производные
- 22. 4. Логарифмическая функция Автор: И. В. Дайняк, к.т.н., доцент кафедры высшей математики БГУИР Дифференциальное исчисление Производные
- 23. 5. Тригонометрические функции Автор: И. В. Дайняк, к.т.н., доцент кафедры высшей математики БГУИР Дифференциальное исчисление Производные
- 24. 5. Тригонометрические функции Автор: И. В. Дайняк, к.т.н., доцент кафедры высшей математики БГУИР Дифференциальное исчисление Производные
- 25. 5. Тригонометрические функции Автор: И. В. Дайняк, к.т.н., доцент кафедры высшей математики БГУИР Дифференциальное исчисление Производные
- 26. 5. Тригонометрические функции Автор: И. В. Дайняк, к.т.н., доцент кафедры высшей математики БГУИР Дифференциальное исчисление Производные
- 28. Скачать презентацию



















 КВН Знатоки математики
КВН Знатоки математики Понятие отношения
Понятие отношения Тема 1.3 Транспортная задача
Тема 1.3 Транспортная задача Презентация по математике, 2 класс
Презентация по математике, 2 класс Действия с десятичными дробями и
Действия с десятичными дробями и Статистиката като наука и практика
Статистиката като наука и практика Трикутник. Види трикутників
Трикутник. Види трикутників Математика навколо нас
Математика навколо нас Прямолинейное и криволинейное движение
Прямолинейное и криволинейное движение Занятие по математике в средней группе по теме: Геометрические фигуры
Занятие по математике в средней группе по теме: Геометрические фигуры Своя игра по математике
Своя игра по математике Длина окружности
Длина окружности Тригонометрические неравенства
Тригонометрические неравенства Квадратные корни. Тренажер
Квадратные корни. Тренажер Решение неравенств и систем неравенств с одной переменной
Решение неравенств и систем неравенств с одной переменной Теорема о трёх перпендикулярах. Задачи на готовых чертежах
Теорема о трёх перпендикулярах. Задачи на готовых чертежах группа комплексные числа
группа комплексные числа Подготовка к введению задач в 2 действия А
Подготовка к введению задач в 2 действия А Построение графиков тригонометрических функций y=sinx и y=cosx
Построение графиков тригонометрических функций y=sinx и y=cosx Решение уравнений
Решение уравнений Система подготовки к ЕГЭ
Система подготовки к ЕГЭ Магические квадраты
Магические квадраты Геометрический материал в рамках образовательной системы Гармония (1-4 классы)
Геометрический материал в рамках образовательной системы Гармония (1-4 классы) Найразумнiший. Правила гри
Найразумнiший. Правила гри Максиминный критерий Вальда
Максиминный критерий Вальда Графики функций синуса и косинуса
Графики функций синуса и косинуса Прием сложения с переходом через десяток
Прием сложения с переходом через десяток Свойства сложения
Свойства сложения