Содержание
- 2. Correlation Correlation A relationship between two variables. The data can be represented by ordered pairs (x,
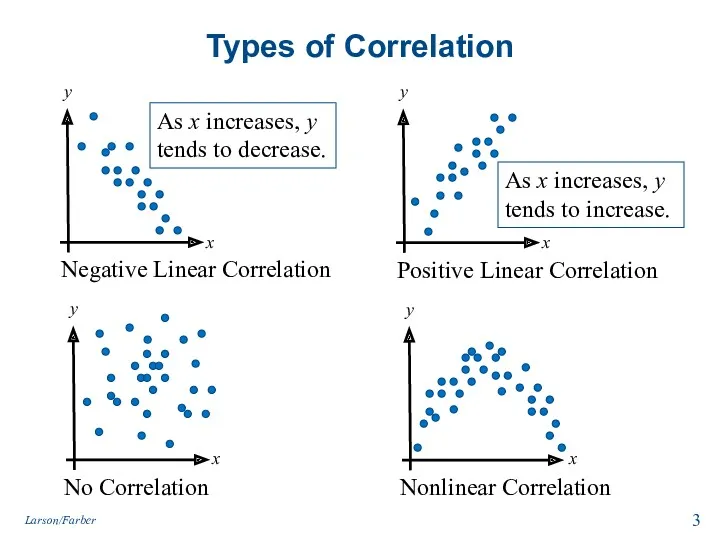
- 3. Types of Correlation Negative Linear Correlation No Correlation Positive Linear Correlation Nonlinear Correlation As x increases,
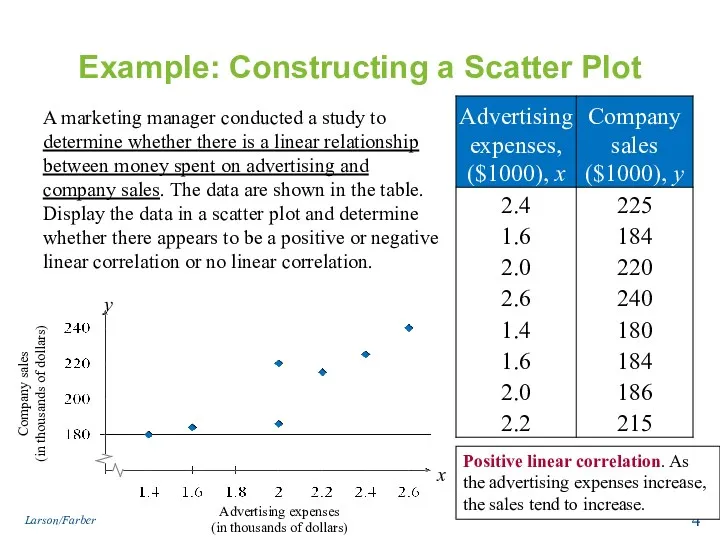
- 4. Example: Constructing a Scatter Plot A marketing manager conducted a study to determine whether there is
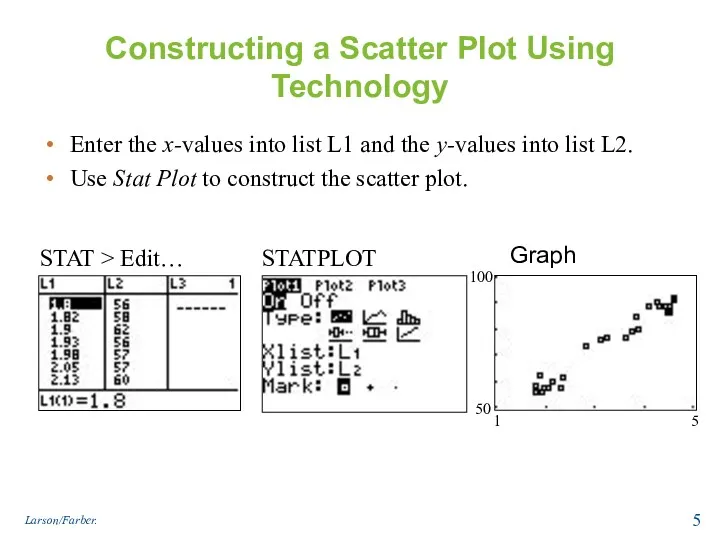
- 5. Constructing a Scatter Plot Using Technology Enter the x-values into list L1 and the y-values into
- 6. Correlation Coefficient Correlation coefficient A measure of the strength and the direction of a linear relationship
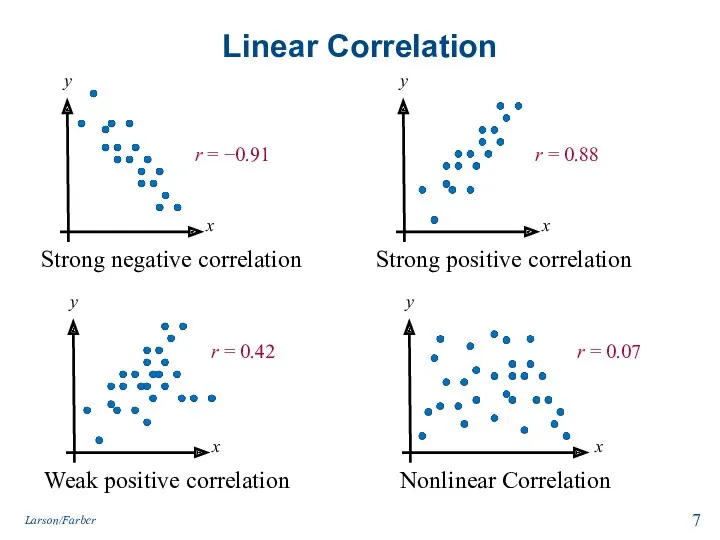
- 7. Linear Correlation Strong negative correlation Weak positive correlation Strong positive correlation Nonlinear Correlation r = −0.91
- 8. Calculating a Correlation Coefficient Find the sum of the x-values. Find the sum of the y-values.
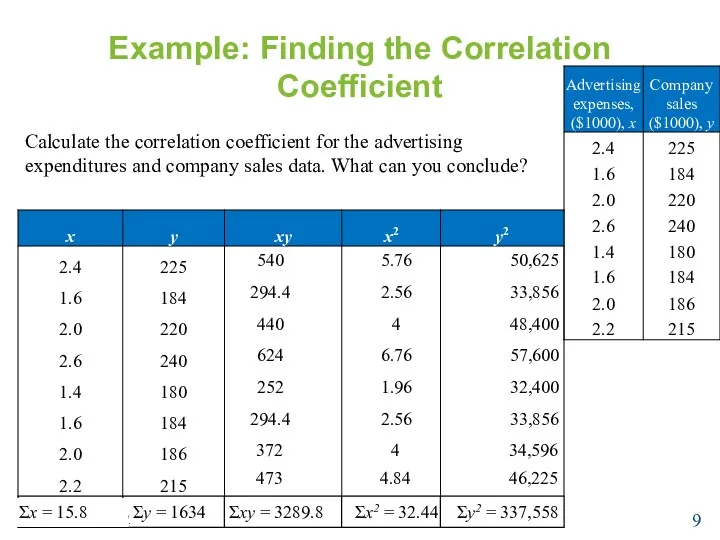
- 9. Example: Finding the Correlation Coefficient Calculate the correlation coefficient for the advertising expenditures and company sales
- 10. Finding the Correlation Coefficient Example Continued… Σx = 15.8 Σy = 1634 Σxy = 3289.8 Σx2
- 11. Using a Table to Test a Population Correlation Coefficient ρ Once the sample correlation coefficient r
- 12. Hypothesis Testing for a Population Correlation Coefficient ρ A hypothesis test (one or two tailed) can
- 13. Using the t-Test for ρ State the null and alternative hypothesis. Specify the level of significance.
- 14. Example: t-Test for a Correlation Coefficient For the advertising data, we previously calculated r ≈ 0.9129.
- 15. Correlation and Causation The fact that two variables are strongly correlated does not in itself imply
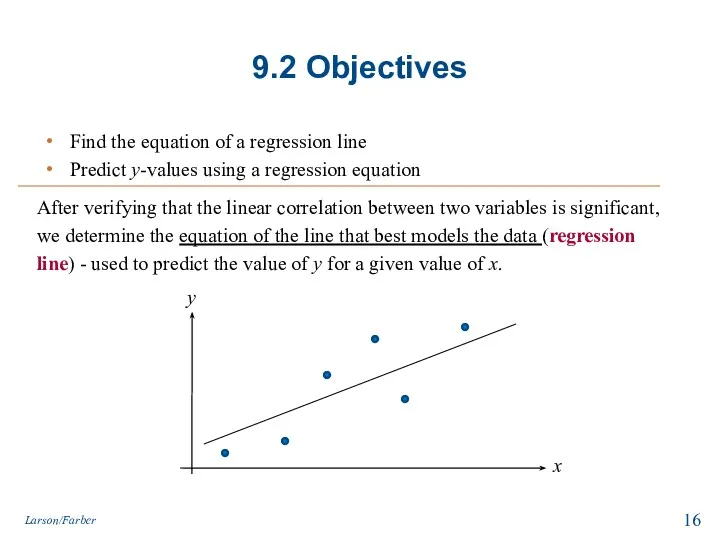
- 16. 9.2 Objectives Find the equation of a regression line Predict y-values using a regression equation Larson/Farber
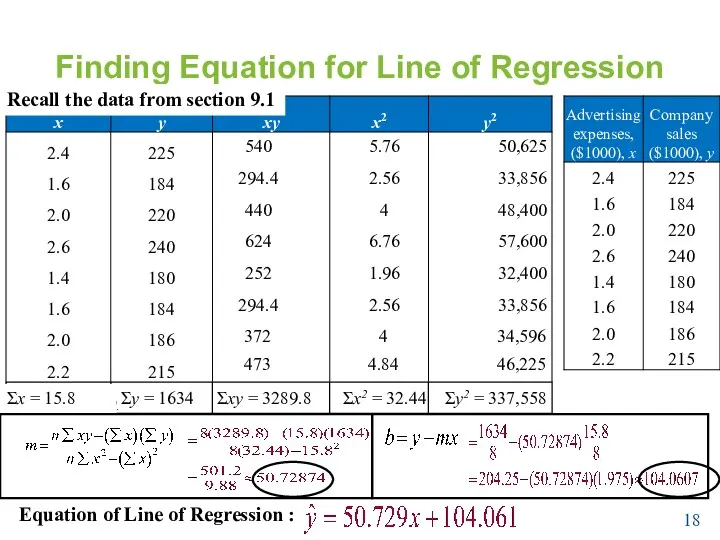
- 17. Residuals & Equation of Line of Regression Residual The difference between the observed y-value and the
- 18. Finding Equation for Line of Regression Larson/Farber 4th ed. 540 294.4 440 624 252 294.4 372
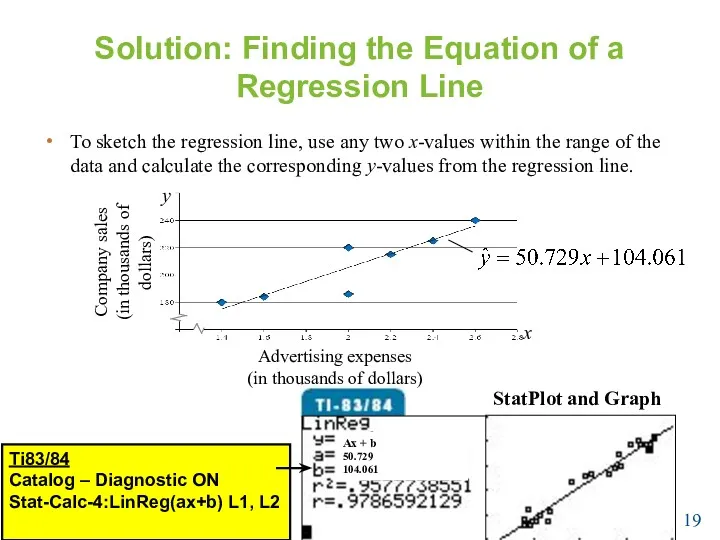
- 19. Solution: Finding the Equation of a Regression Line To sketch the regression line, use any two
- 20. Example: Predicting y-Values Using Regression Equations The regression equation for the advertising expenses (in thousands of
- 21. 9.3 Measures of Regression and Prediction Intervals (Objectives) Interpret the three types of variation about a
- 22. Total variation = The sum of the squares of the differences between the y-value of each
- 23. The Standard Error of Estimate Standard error of estimate The standard deviation (se )of the observed
- 25. Скачать презентацию














 Натуральные числа. Обозначение натуральных чисел
Натуральные числа. Обозначение натуральных чисел Геометрический смысл производной. Задачи типа В8 в ЕГЭ
Геометрический смысл производной. Задачи типа В8 в ЕГЭ Презентация Деление с остатком
Презентация Деление с остатком Доли. Обыкновенные дроби. 5 класс
Доли. Обыкновенные дроби. 5 класс Единицы времени УМК Гармония 4 класс УМК Гармония
Единицы времени УМК Гармония 4 класс УМК Гармония Конструирование системы задач по теме Линейная функция
Конструирование системы задач по теме Линейная функция ОТКРЫТЫЙ УРОК ПО МАТЕМАТИКЕ В 4 А КЛАССЕ ПО ТЕМЕ: АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ НАД ЧИСЛАМИ
ОТКРЫТЫЙ УРОК ПО МАТЕМАТИКЕ В 4 А КЛАССЕ ПО ТЕМЕ: АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ НАД ЧИСЛАМИ Решение систем линейных уравнений с двумя переменными
Решение систем линейных уравнений с двумя переменными Знаходження числа за його відсотком
Знаходження числа за його відсотком Франсуа Виет
Франсуа Виет Дерево возможных вариантов
Дерево возможных вариантов Математика. Основные разделы теста. 1 семестр
Математика. Основные разделы теста. 1 семестр Круги Эйлера в решении задач
Круги Эйлера в решении задач Одночлены и многочлены
Одночлены и многочлены Закон больших чисел
Закон больших чисел Единицы времени УМК Гармония 4 класс УМК Гармония
Единицы времени УМК Гармония 4 класс УМК Гармония Задачи на увеличение и уменьшение на несколько единиц
Задачи на увеличение и уменьшение на несколько единиц Состав чисел второго десятка с переходом через десяток
Состав чисел второго десятка с переходом через десяток Многоугольники. Четырехугольники
Многоугольники. Четырехугольники Григорий Яковлевич Перельман
Григорий Яковлевич Перельман Решение задач. 1 класс
Решение задач. 1 класс Действия с рациональными числами
Действия с рациональными числами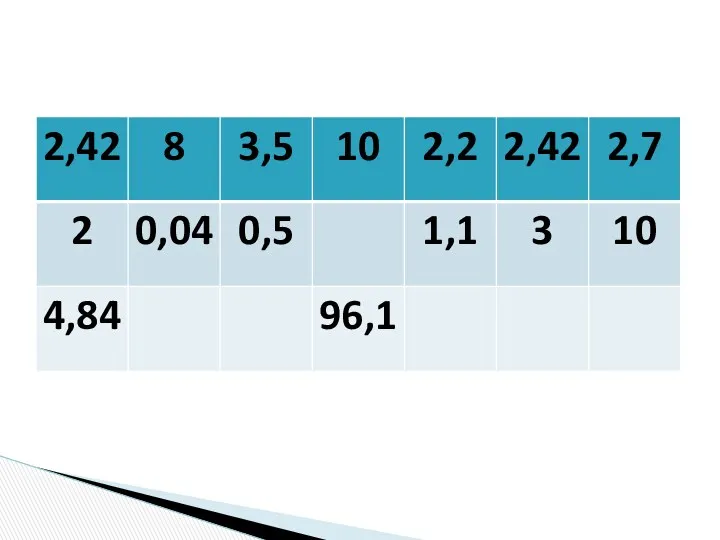 Умножение десятичных дробей
Умножение десятичных дробей Что такое топология. Лист Мёбиуса
Что такое топология. Лист Мёбиуса Комплексные числа. Типовой вариант самостоятельной работы
Комплексные числа. Типовой вариант самостоятельной работы Сложение натуральных чисел и его свойства
Сложение натуральных чисел и его свойства Задания типа С5
Задания типа С5 Период радиоактивного распада. Решение задач. Интегрированный урок физика+математика 11 класс
Период радиоактивного распада. Решение задач. Интегрированный урок физика+математика 11 класс