Содержание
- 2. Основные вопросы: Понятие производной. Геометрический и физический смысл. Понятие сложной функции. Производная сложной функции. Производные высших
- 3. Предел отношения приращения функции к приращению аргумента при условии, что - называется производной данной функции и
- 4. Операция вычисления производной называется дифференци-рованием. Функция называется дифференци-руемой в данной точке, если в этой точке существует
- 5. Геометрический и физический смысл производной.
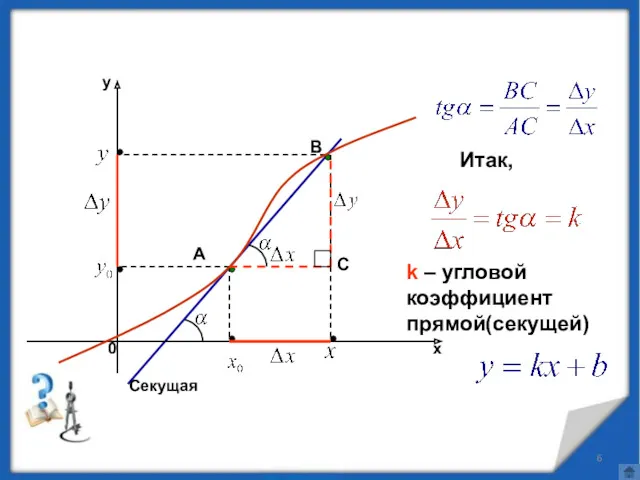
- 6. A B Секущая С Итак, k – угловой коэффициент прямой(секущей)
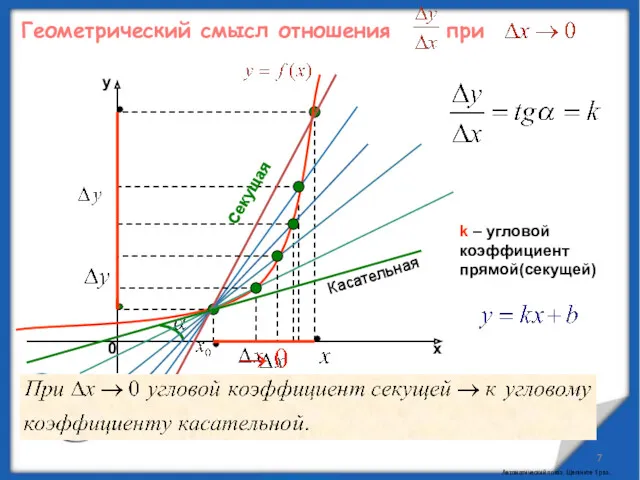
- 7. Геометрический смысл отношения при k – угловой коэффициент прямой(секущей) Секущая стремится занять положение касательной. То есть,
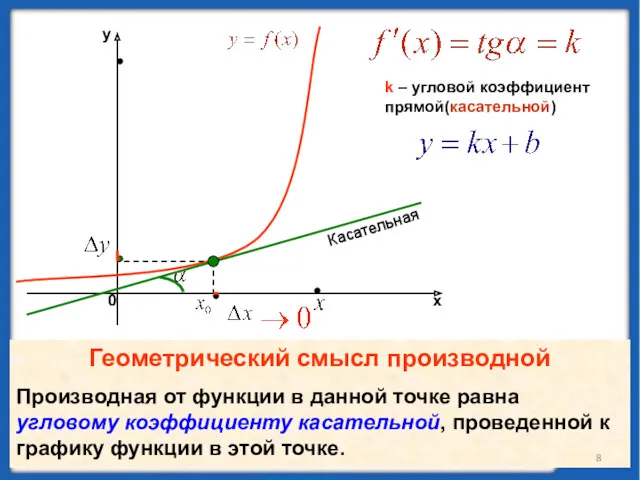
- 8. k – угловой коэффициент прямой(касательной) Касательная Геометрический смысл производной Производная от функции в данной точке равна
- 9. Если материальная точка движется прямолинейно и ее координата изменяется по закону x(t), то скорость ее движения
- 10. Точка движется прямолинейно по закону Вычислите скорость движения точки: а) в момент времени t; б) в
- 11. Найдите скорость и ускорение для точки, движущейся по закону а) в момент времени t; б) в
- 12. 1. Производная от числа (константы) равна нулю.
- 13. 3. Производная алгебраической суммы (разности) функций равна алгебраической сумме производных этих функций:
- 14. 4. Производная произведения 2-х функций равна сумме произведений каждой из этих функций на производную другой:
- 15. 5. Производная частного 2-х функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя
- 16. 6. Постоянный множитель C можно выносить из-под знака производной:
- 17. Производная показательной функции Показательная функция дифференцируема в каждой точке области определения, и Функция дифференцируема в каждой
- 18. Производные некоторых элементарных функций. =
- 19. Производные обратных тригонометрических функций
- 20. Задание 1. Задание 2.
- 21. Задание 3. Задание 4.
- 22. Задание 5 Задание 6
- 23. Задание 7 Задание 8
- 24. Сложная функция: Примеры: Правило нахождения производной сложной функции (производная сложной функции равна производной основной функции на
- 25. Сложная функция: Правило нахождения производной сложной функции (производная сложной функции равна производной основной функции на производную
- 26. Сложная функция: Правило нахождения производной сложной функции (производная сложной функции равна производной основной функции на производную
- 27. Сложная функция: Правило нахождения производной сложной функции (производная сложной функции равна производной основной функции на производную
- 28. Сложная функция: Правило нахождения производной сложной функции (производная сложной функции равна производной основной функции на производную
- 30. Таблица производных для сложной функции
- 31. Производные высших порядков
- 32. Применение производной к исследованию функции
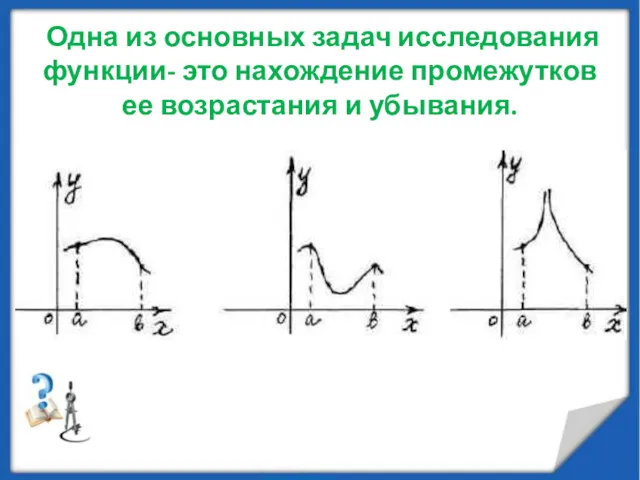
- 33. Одна из основных задач исследования функции- это нахождение промежутков ее возрастания и убывания.
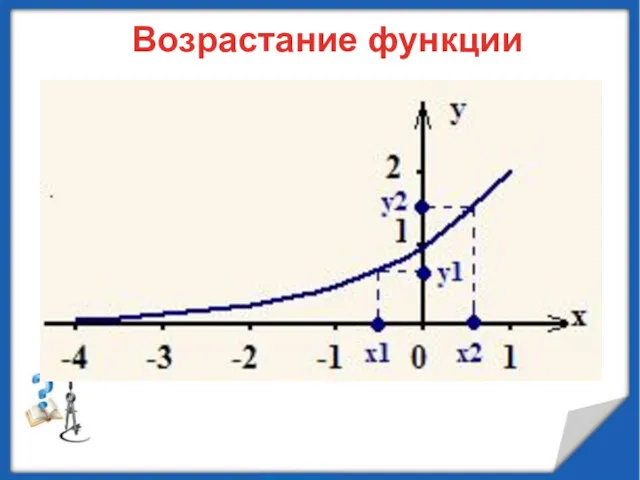
- 34. Возрастание функции
- 35. ОПРЕДЕЛЕНИЕ 1: Функция f (x) называется возрастающей на промежутке D, если для любых чисел x1 и
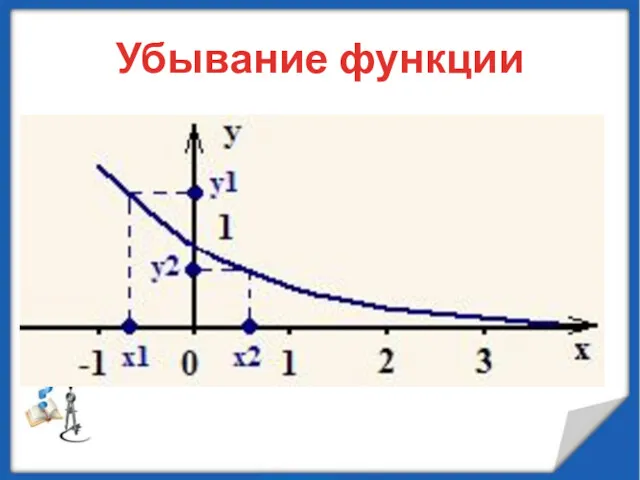
- 36. Убывание функции
- 37. ОПРЕДЕЛЕНИЕ 2: Функция f (x) называется убывающей на промежутке D, если для любых чисел x1 и
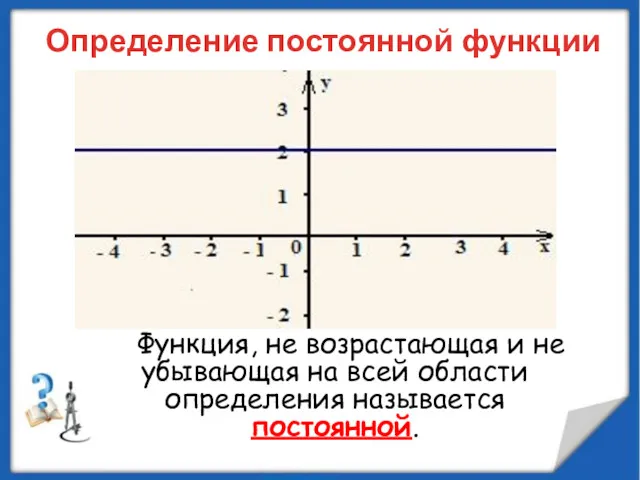
- 38. Определение постоянной функции Функция, не возрастающая и не убывающая на всей области определения называется постоянной.
- 39. Промежутки монотонности Промежутки возрастания и убывания называются промежутками монотонности функции. Если функция возрастает или убывает на
- 40. ТЕОРЕМА 1.(необходимые условия возрастания и убывания функции). Если дифференцируемая функция у = f(x), x ∈(а,b) возрастает
- 41. ТЕОРЕМА 2.(достаточный признак возрастания и убывания функций). Если f’(x)>0, в каждой точке интервала (a,b), то функция
- 42. Точки области определения функции, в которых производная функции равна нулю или не существует, называются КРИТИЧЕСКИМИ ТОЧКАМИ.
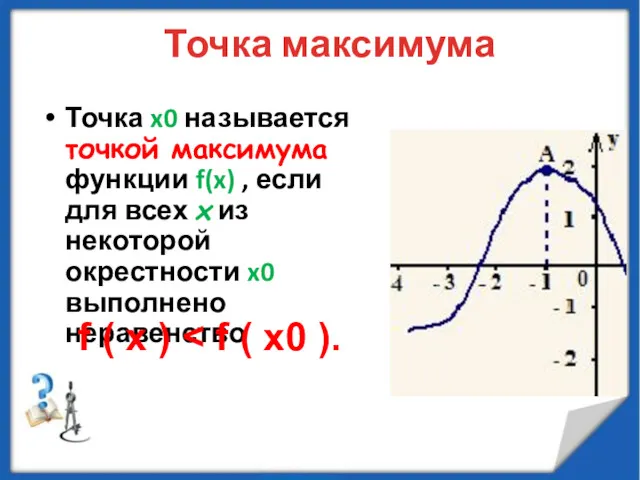
- 43. Точка максимума Точка x0 называется точкой максимума функции f(x) , если для всех x из некоторой
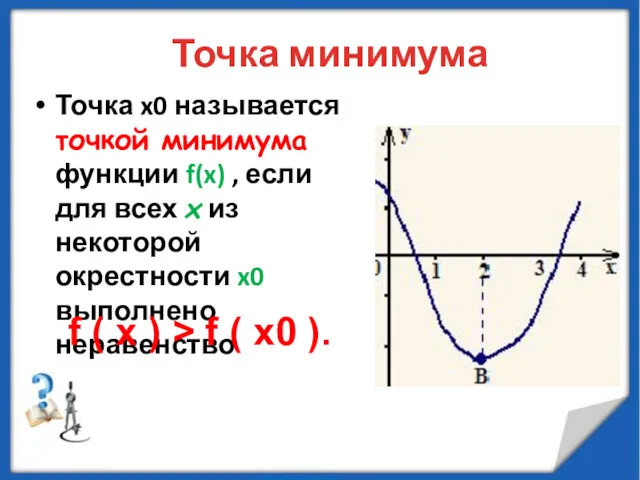
- 44. Точка минимума Точка x0 называется точкой минимума функции f(x) , если для всех x из некоторой
- 45. Точки максимума и минимума функции f(x) называются точками экстремума этой функции, а значения функции в точках
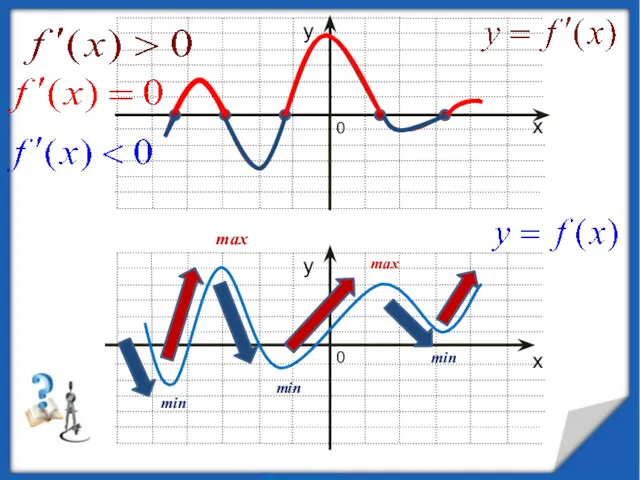
- 46. 0 0 min max min min max
- 47. Экстремум функции, если он существует, может быть только в критических точках. Однако не во всякой критической
- 48. ТЕОРЕМА 3.(необходимое условие экстремума). Если функция у = f(х) имеет экстремум в точке х = а,
- 49. Если производная f ' (х) при переходе через точку х0 меняет знак с «+» на «-»,
- 50. 1).Найти область определения функции: D(f). 2). Найти f’(x). 3).Найти точки, в которых выполняется равенство f’(x)=0 4).
- 51. 5).Отметить на координатной прямой все критические точки и область определения функции y=f(x); получаются промежутки области определения
- 52. 7). Сделать выводы о наличии или отсутствии экстремума в каждой из критических точек: если знак производной
- 53. ПРИМЕР . ИССЛЕДОВАТЬ НА ЭКСТРЕМУМ ФУНКЦИЮ У = 2Х3 – 15Х2 + 36Х + 1 1.
- 54. Исследование функций с помощью второй производной 04.11.2018
- 55. 04.11.2018
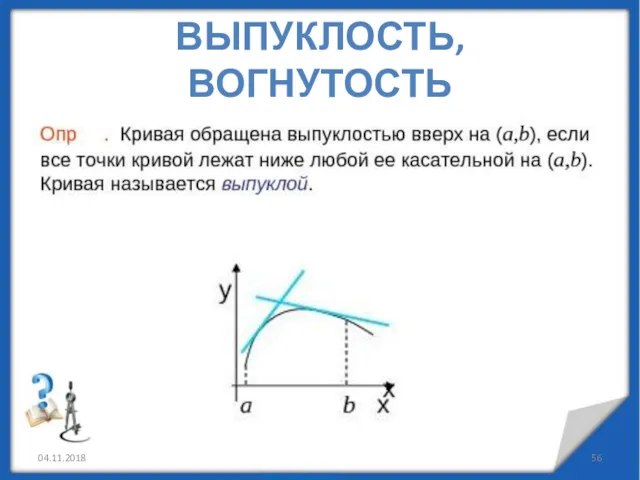
- 56. ВЫПУКЛОСТЬ, ВОГНУТОСТЬ 04.11.2018
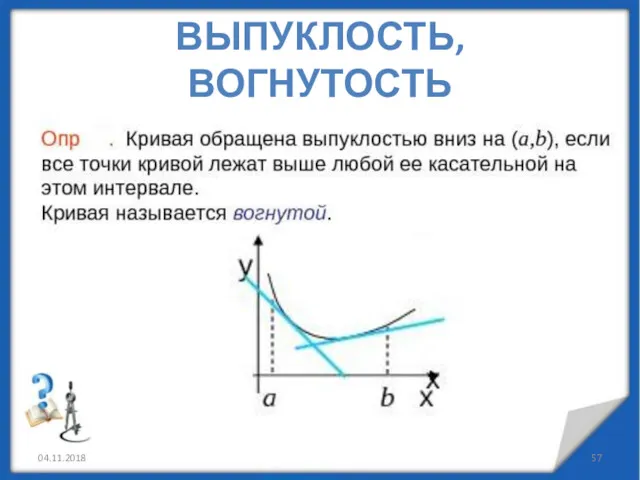
- 57. 04.11.2018 ВЫПУКЛОСТЬ, ВОГНУТОСТЬ
- 58. 04.11.2018 ВЫПУКЛОСТЬ, ВОГНУТОСТЬ
- 59. Пример 04.11.2018
- 60. 04.11.2018 http://aida.ucoz.ru
- 61. 04.11.2018
- 62. Домашнее задание:
- 63. Домашнее задание:
- 65. Скачать презентацию


















































 Математика в моей будущей профессии металлурга
Математика в моей будущей профессии металлурга Тригонометрическая окружность. Тригонометрические функции
Тригонометрическая окружность. Тригонометрические функции Современные методы исследования динамических режимов работы асинхронных двигателей. Магистерская диссертация
Современные методы исследования динамических режимов работы асинхронных двигателей. Магистерская диссертация Расчетно-пояснительная записка
Расчетно-пояснительная записка Прямая и обратная пропорциональность
Прямая и обратная пропорциональность Решение систем линейных уравнений
Решение систем линейных уравнений Площадь криволинейной трапеции и интеграл
Площадь криволинейной трапеции и интеграл Учимся определять время по часам
Учимся определять время по часам Олимпиада Юный математик 4 класс
Олимпиада Юный математик 4 класс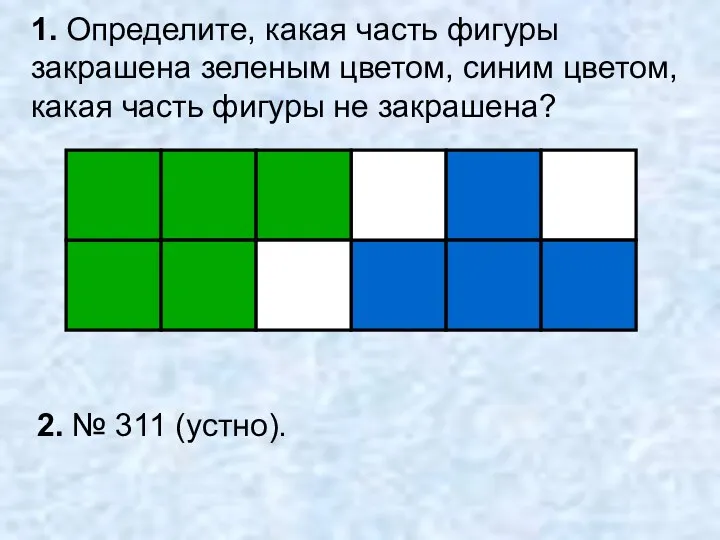 Правило сравнения дробей с одинаковыми знаменателями
Правило сравнения дробей с одинаковыми знаменателями Второй и третий признаки равенства треугольников. 7 класс
Второй и третий признаки равенства треугольников. 7 класс Простейшие задачи в координатах
Простейшие задачи в координатах Используемые математические знания
Используемые математические знания Решение тригонометрического уравнения (С 1, 27)
Решение тригонометрического уравнения (С 1, 27) Решение уравнений. Урок 69
Решение уравнений. Урок 69 Что узнали, чему научились. Урок математики 2 класс
Что узнали, чему научились. Урок математики 2 класс Свойства прямоугольного треугольника. Геометрия 7 класс
Свойства прямоугольного треугольника. Геометрия 7 класс Логические задачи в таблицах
Логические задачи в таблицах Действия с дробями. Сложение дробей. Свойства сложения
Действия с дробями. Сложение дробей. Свойства сложения Интересные математические факты
Интересные математические факты Решение неравенств
Решение неравенств Смешанные числа
Смешанные числа Математическая регата. Викторина для семиклассников
Математическая регата. Викторина для семиклассников Сложение и вычитание смешанных чисел. Устный счет. Открытый урок. 5 класс
Сложение и вычитание смешанных чисел. Устный счет. Открытый урок. 5 класс Calculation of the determinants + verifiation
Calculation of the determinants + verifiation Приближенные значения чисел. Округление чисел
Приближенные значения чисел. Округление чисел формирование Икт компетентности. 5 класс
формирование Икт компетентности. 5 класс Путешествие в космос
Путешествие в космос