Слайд 2

Требуется найти решение ДУ n-го порядка
удовлетворяющего заданным начальным условиям:
Лекция 12
ДУ высших порядков.
Слайд 3

Слайд 4

Частное решение ДУ (решение задачи Коши) может быть найдено из общего
решения по заданным начальным условиям, из которых получают систему уравнений для определения постоянных
Слайд 5

Решение задачи Коши ДУ n-го порядка имеет вид:
Слайд 6

(правая часть зависит только от х)
Общее решение получается путем
n-кратного интегрирования:
Слайд 7
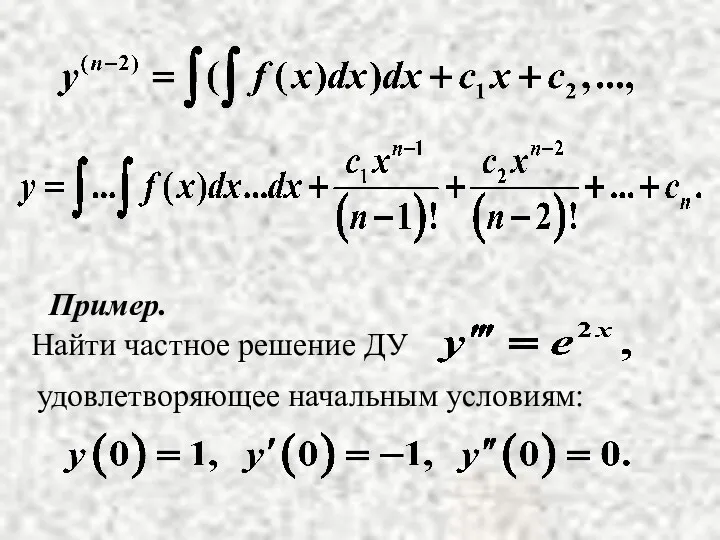
Пример.
удовлетворяющее начальным условиям:
Слайд 8

Слайд 9
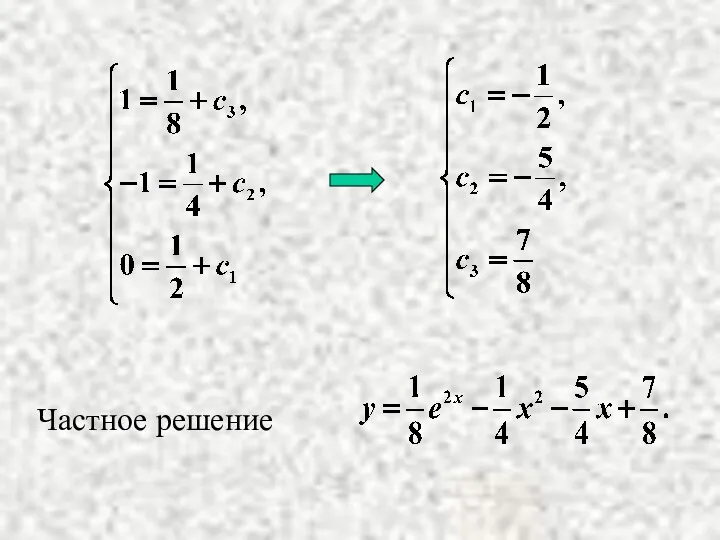
Слайд 10
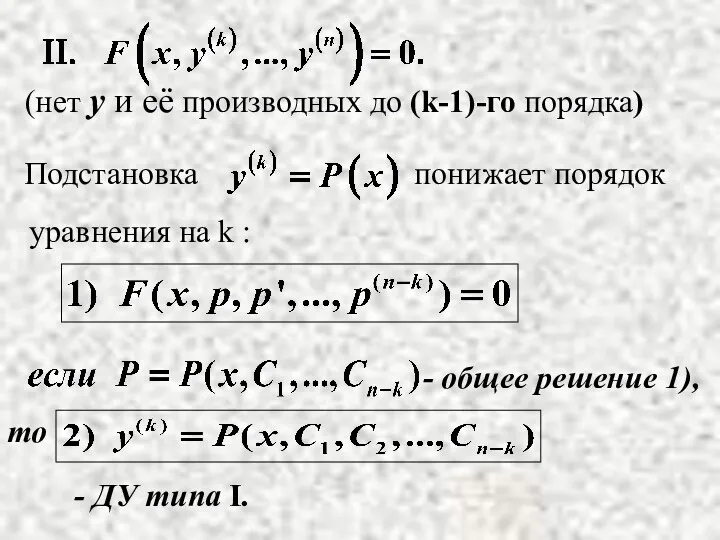
Подстановка понижает порядок
уравнения на k :
- общее решение 1),
то
-
ДУ типа I.
Слайд 11

Слайд 12
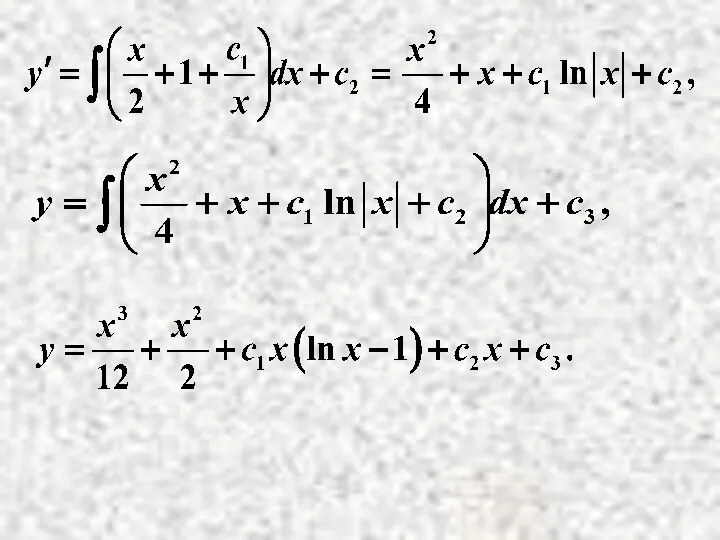
Слайд 13

(Уравнение не содержит х).
понижает порядок уравнения на 1.
Слайд 14

Слайд 15
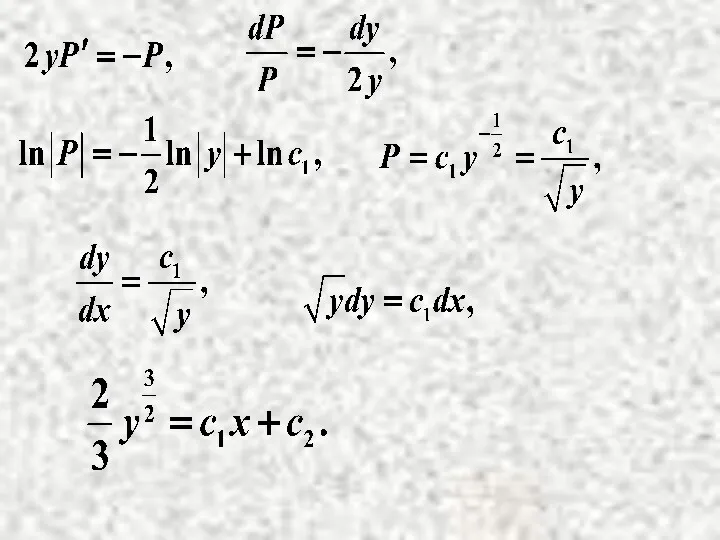
Слайд 16

Интегрирование понижает порядок уравнения на единицу.
Пример.
Решение.
Слайд 17
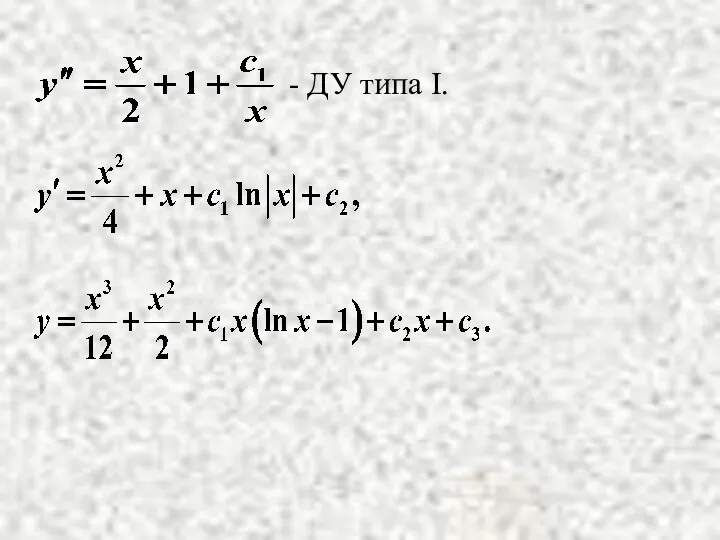
Слайд 18

Слайд 19

Линейное дифференциальное уравнение называется неоднородным (НЛДУ) если оно
имеет вид:
Слайд 20

Рассмотрим ОЛДУ второго порядка:
- частные решения ДУ.
Слайд 21
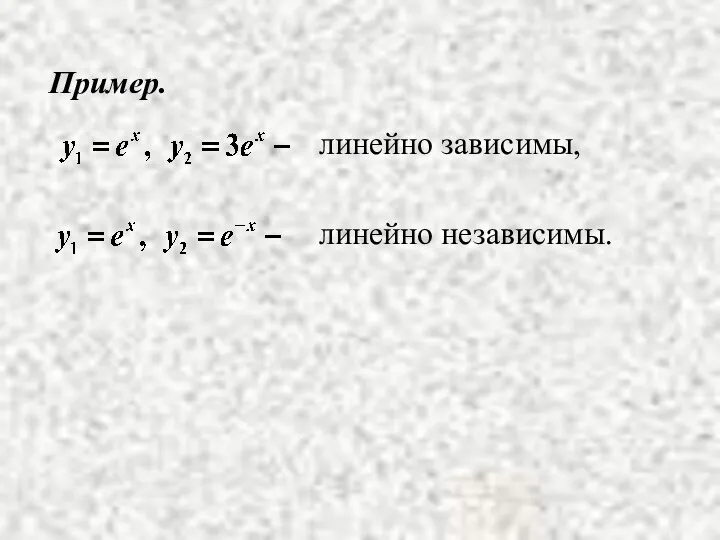
Пример.
линейно зависимы,
линейно независимы.
Слайд 22

то
называется определителем Вронского.
Доказательство:
Слайд 23
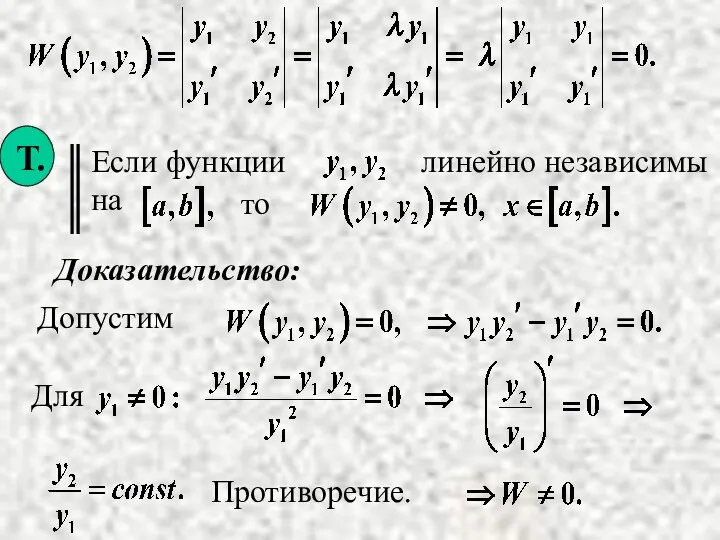
то
Допустим
Доказательство:
Противоречие.
Слайд 24

то общее решение этого
Доказательство:
уравнения равно их линейной комбинации:
Слайд 25

Докажем, что при любых начальных условиях
удовлетворяло этим начальным условиям.
Пусть
Слайд 26

Слайд 27






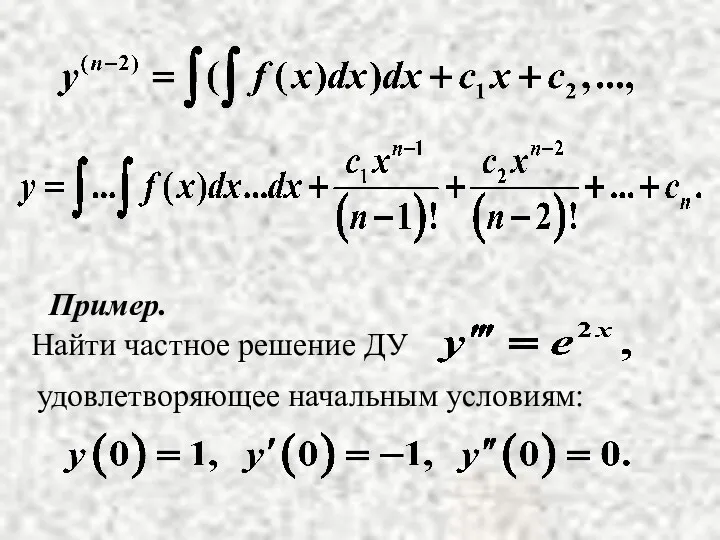


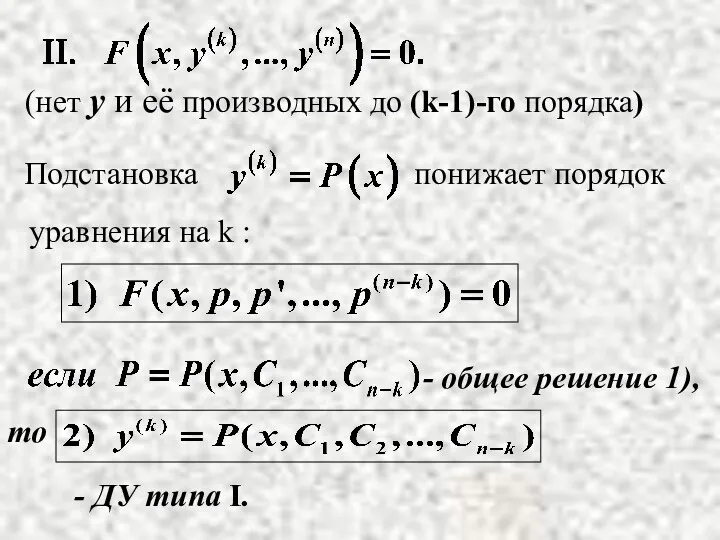

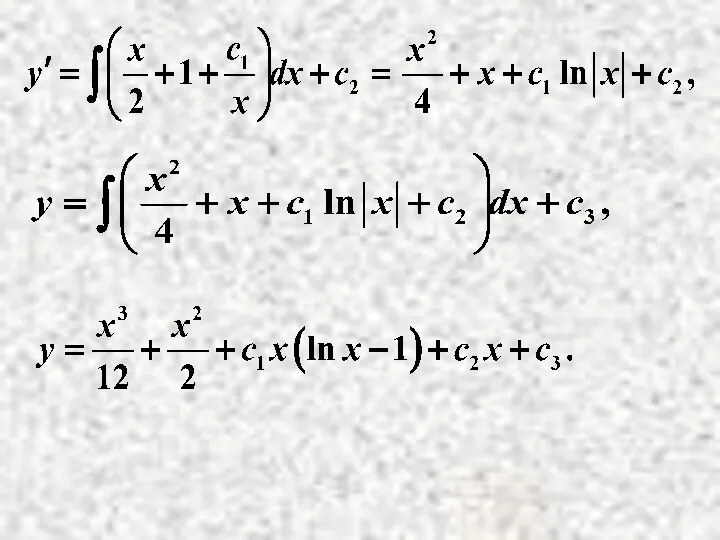


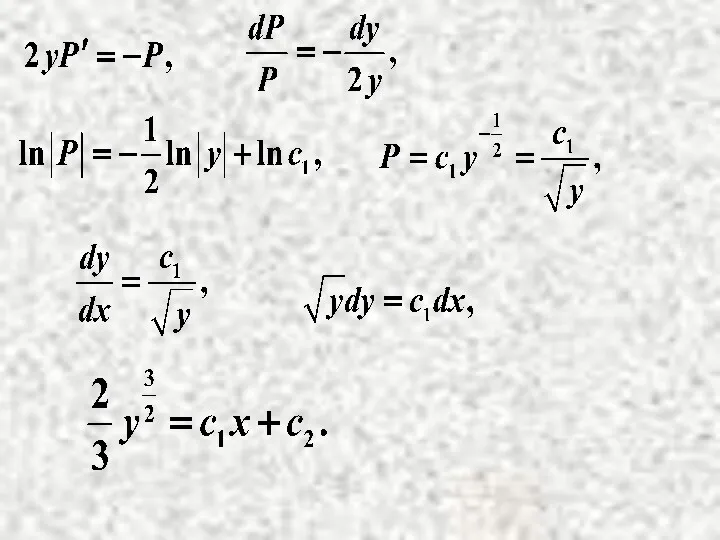

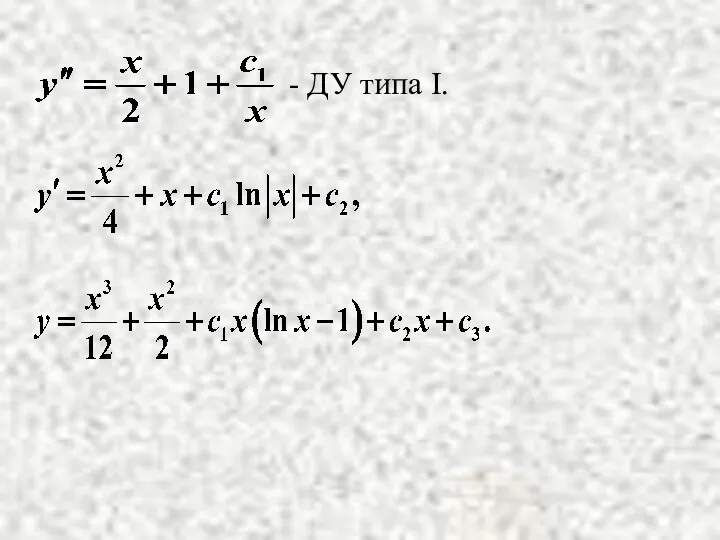



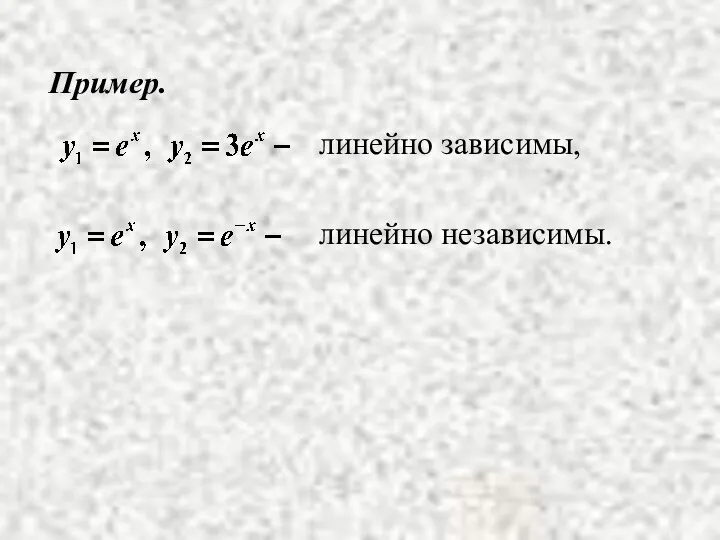

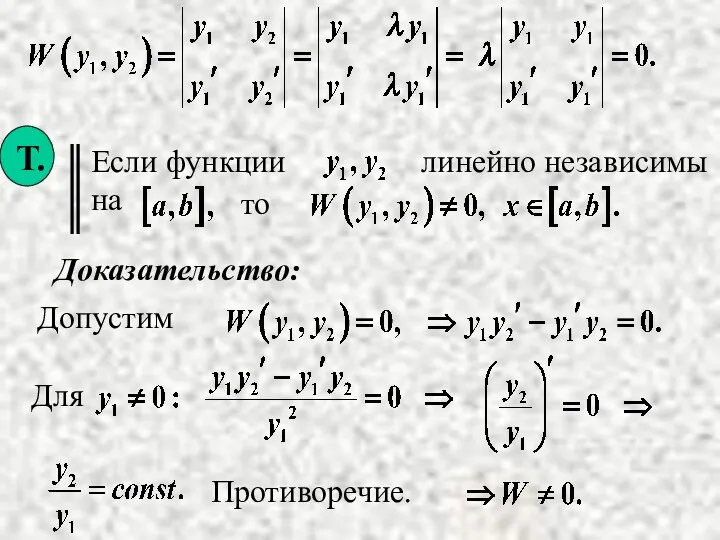




 Решение систем уравнений второй степени с двумя переменными методом сложения
Решение систем уравнений второй степени с двумя переменными методом сложения Рациональные числа
Рациональные числа Презентация по математике Периметр и Площадь прямоугольника
Презентация по математике Периметр и Площадь прямоугольника Основы теории надежности
Основы теории надежности Аксиомы планиметрии
Аксиомы планиметрии Вписанные и описанные окружности
Вписанные и описанные окружности Умножение на число 4
Умножение на число 4 Угол между прямой и плоскостью
Угол между прямой и плоскостью Векторы. Векторная и скалярная величины
Векторы. Векторная и скалярная величины Пропорциональные отрезки в прямоугольном треугольнике
Пропорциональные отрезки в прямоугольном треугольнике Китайская система счисления
Китайская система счисления Задачи по математике.
Задачи по математике. Повторення вивченого. Робота з малюнками й текстами (урок № 137)
Повторення вивченого. Робота з малюнками й текстами (урок № 137) Понятие о движении плоскости. Центральная и осевая симметрии. 9 класс
Понятие о движении плоскости. Центральная и осевая симметрии. 9 класс Синус, косинус и тангенс угла
Синус, косинус и тангенс угла Вправи й задачі на засвоєння таблиць додавання і віднімання числа 7. Розпізнавання геометричних фігур
Вправи й задачі на засвоєння таблиць додавання і віднімання числа 7. Розпізнавання геометричних фігур История возникновения и развития геометрии
История возникновения и развития геометрии Окружность и круг
Окружность и круг Математическое образование в современном мире
Математическое образование в современном мире Теория вероятностей. Достоверные, невозможные, случайные события
Теория вероятностей. Достоверные, невозможные, случайные события Таблица вариантов. Правило произведения, графы
Таблица вариантов. Правило произведения, графы Интерактивный тест по теме Тысяча. Нумерация
Интерактивный тест по теме Тысяча. Нумерация Математическая и статистическая обработка данных в ЭТ
Математическая и статистическая обработка данных в ЭТ Перпендикуляр и наклонная. Угол между прямой и плоскостью
Перпендикуляр и наклонная. Угол между прямой и плоскостью Занимательная математика
Занимательная математика Решение задач с помощью уравнений
Решение задач с помощью уравнений Случайные величины. Определение случайной величины (лекция 6)
Случайные величины. Определение случайной величины (лекция 6) Устные способы решения квадратных уравнений. 8 класс
Устные способы решения квадратных уравнений. 8 класс