Содержание
- 2. Определения (a, b) = {a, {a, b}} — упорядоченная пара. (a, b) = (c, d)⇔ a
- 3. Пример A = {1, 2} B = {2, 3, 4} A× B = {(1, 2), (1,
- 4. Отношения Произвольное подмножество A× B называется отношением из A в B. A — область определения. B
- 5. Свойства отношений Пусть на множестве A задано отношение R: рефлексивное, если aRa∀a∈ A; симметричное, если aRb⇒
- 6. Графы Неупорядоченный граф G = (V, E), где: V — множество вершин; E — отношение на
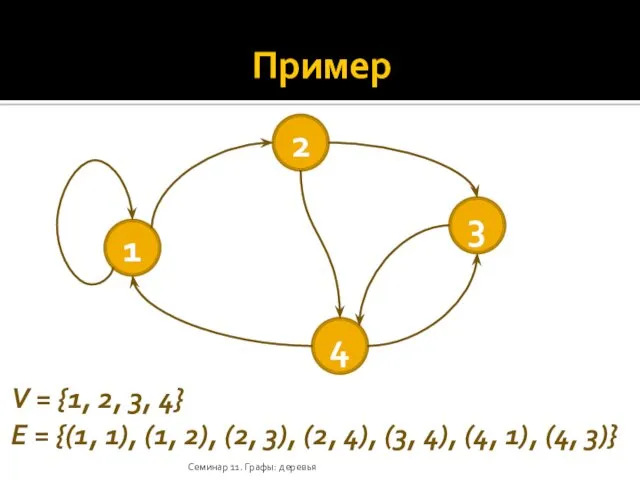
- 7. Пример Семинар 11. Графы: деревья V = {1, 2, 3, 4} E = {(1, 1), (1,
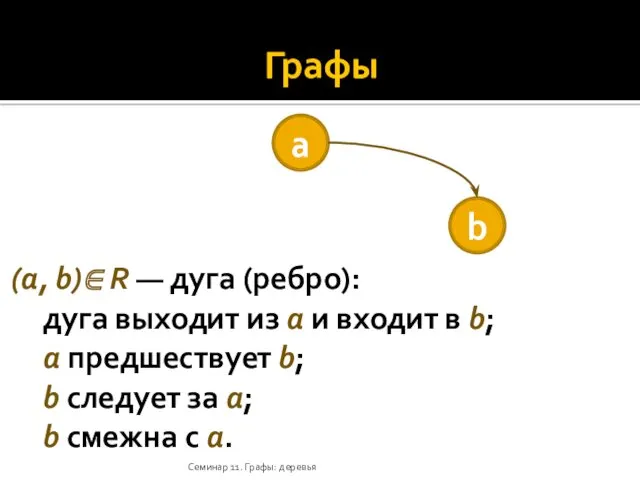
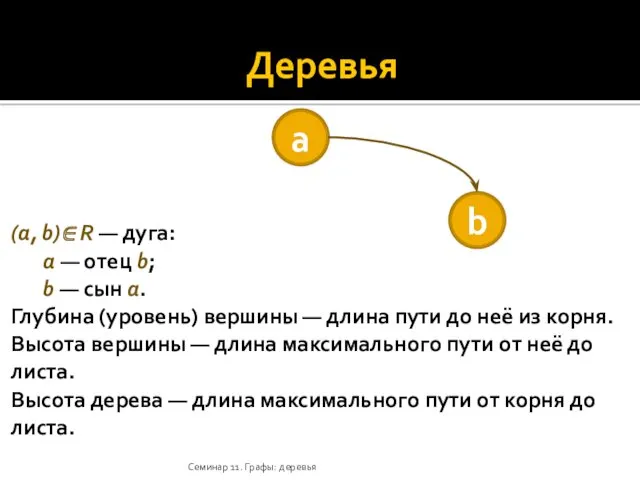
- 8. Графы Семинар 11. Графы: деревья (a, b)∈ R — дуга (ребро): дуга выходит из a и
- 9. Пути в графах Последовательность вершин (a0, a1, a2, …, an), n ≥ 1 называется путём (маршрутом)
- 10. Степень вершины Степень по входу (полустепень входа) вершины — число входящих в неё дуг. Степень по
- 11. Ациклические графы Ациклический граф — орграф без циклов. Вершина с полустепенью входа 0 — базовая. Вершина
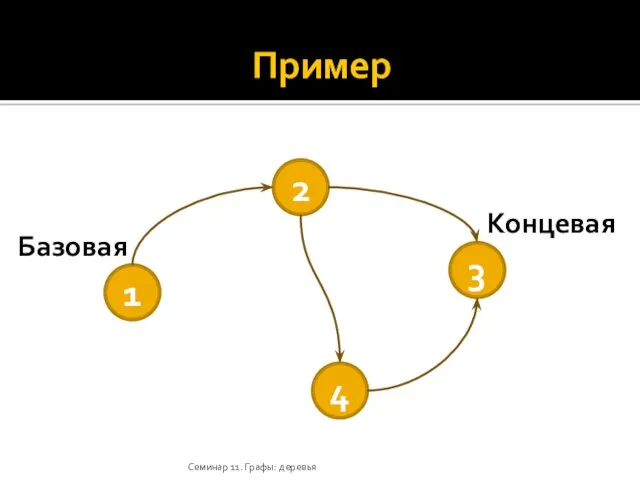
- 12. Пример Семинар 11. Графы: деревья Базовая Концевая
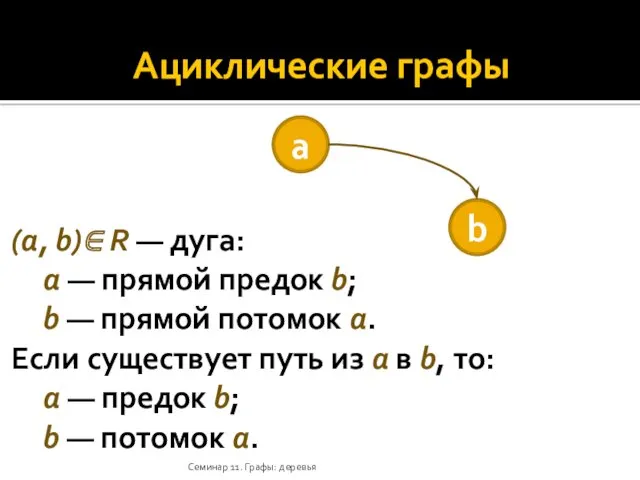
- 13. Ациклические графы Семинар 11. Графы: деревья (a, b)∈ R — дуга: a — прямой предок b;
- 14. Деревья (Ориентированное) дерево — (ориентированный) граф со специальной вершиной r (корнем): полустепень по входу равна 0;
- 15. Поддерево Поддерево дерева T = (V, E) — любое дерево T' = (V', E'): 1. V'
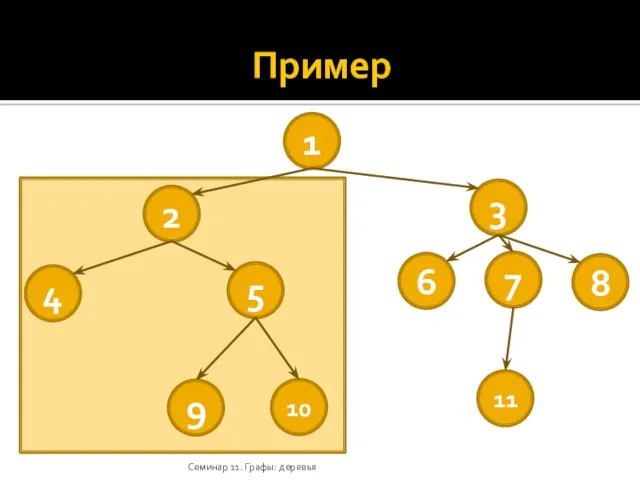
- 16. Пример Семинар 11. Графы: деревья 1 2 3 4 5 6 7 8 9 10 11
- 17. Деревья Семинар 11. Графы: деревья (a, b)∈ R — дуга: a — отец b; b —
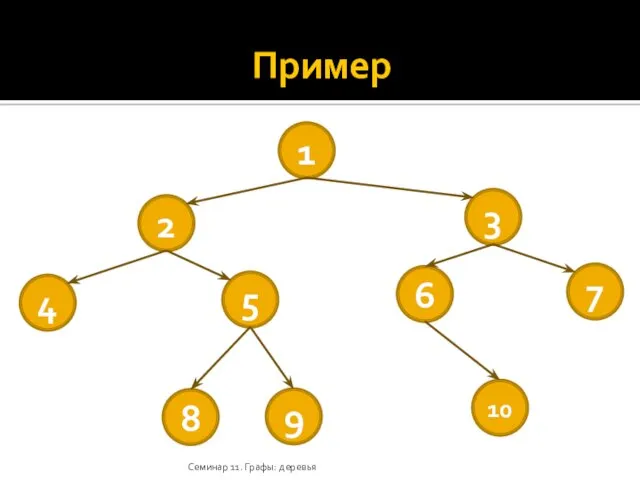
- 18. Бинарные деревья Упорядоченное дерево — дерево, в котором множество сыновей каждой вершины упорядочено слева направо. Бинарное
- 19. Пример Семинар 11. Графы: деревья 1 2 3 4 5 6 7 8 9 10
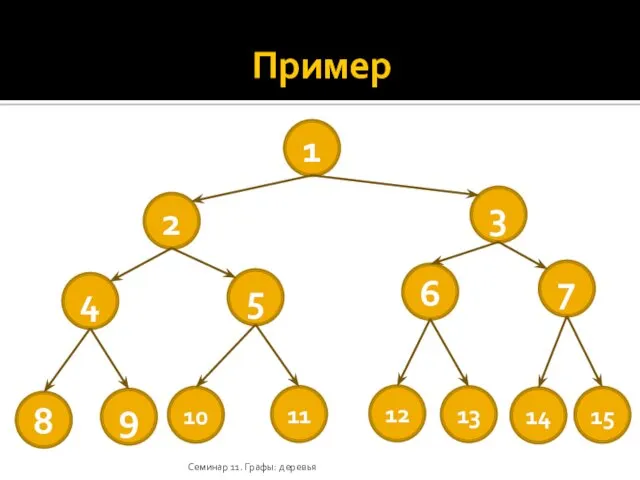
- 20. Бинарные деревья Бинарное дерево полное, если существует целое k, такое что любая вершина глубины меньше k
- 21. Пример Семинар 11. Графы: деревья 1 2 3 4 5 6 7 10 11 12 8
- 22. Представление полных бинарных деревьев Массив T[2k - 2]: T[0] — корень; левый сын вершины i —
- 23. Пример T == {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13,
- 24. Обходы деревьев Обход дерева — способ исследования вершин дерева, при котором каждая вершина проходится только один
- 25. Обходы деревьев в глубину Пусть T — дерево c корнем r, а v1, v2, …, vn
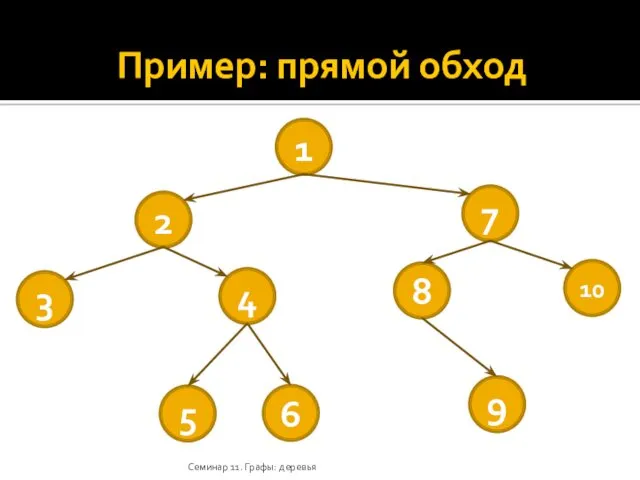
- 26. Пример: прямой обход Семинар 11. Графы: деревья 1 2 7 3 4 8 10 5 6
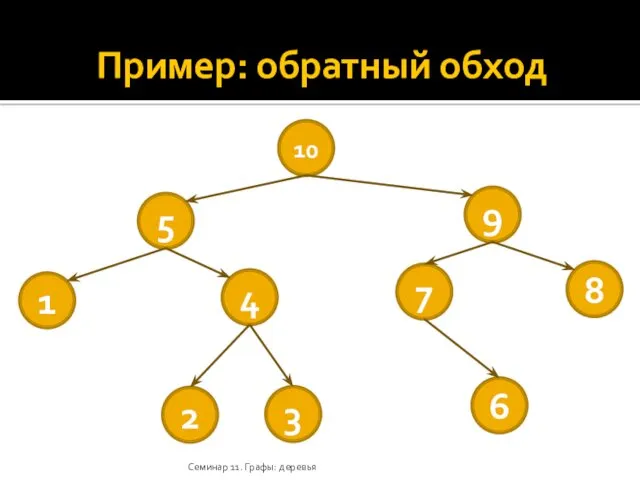
- 27. Пример: обратный обход Семинар 11. Графы: деревья 10 5 9 1 4 7 8 2 3
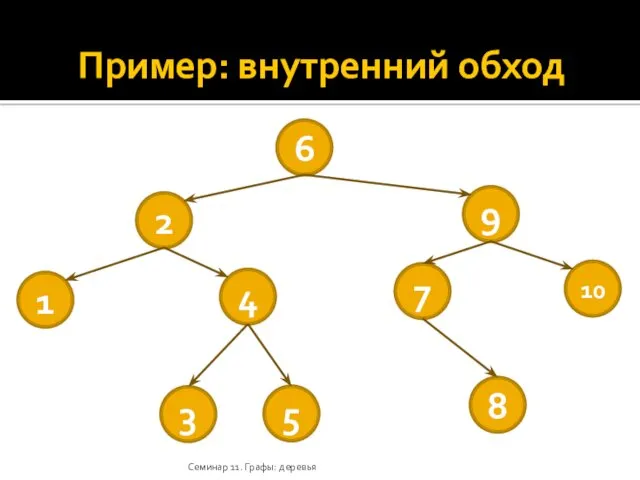
- 28. Пример: внутренний обход Семинар 11. Графы: деревья 6 2 9 1 4 7 10 3 5
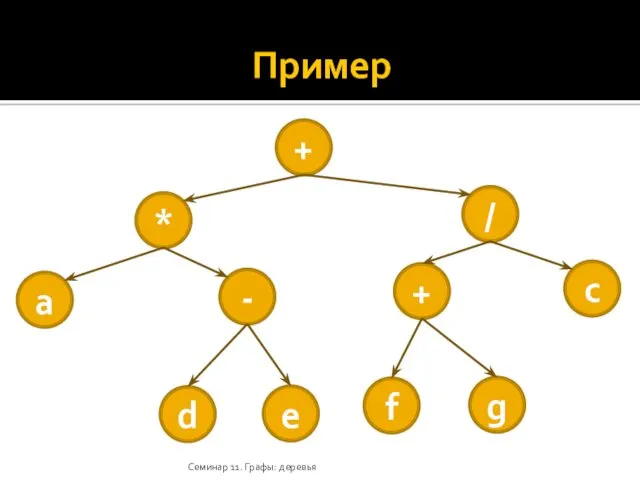
- 29. Пример Семинар 11. Графы: деревья + * / a - + c d e g f
- 30. Пример Префиксный: + * a - d e / + f g c Постфиксный: a d
- 31. Обход в ширину Это обход по уровням, начиная от корня, слева направо (или справа налево). Алгоритм:
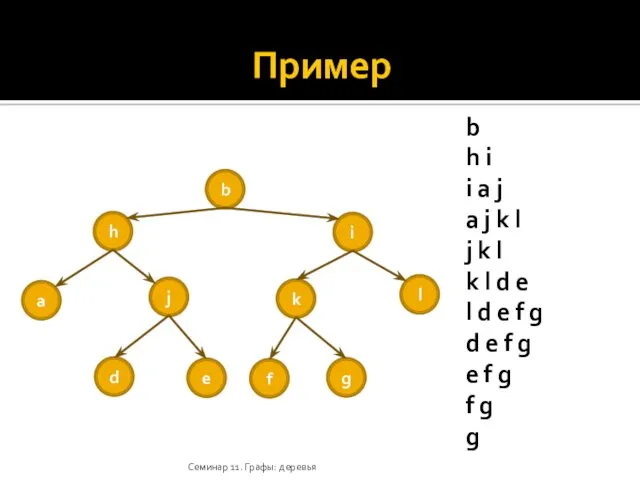
- 32. Пример Семинар 11. Графы: деревья b h i i a j a j k l j
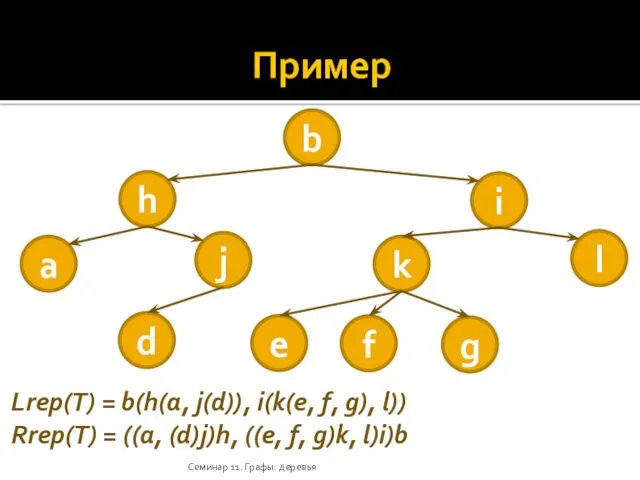
- 33. Представления деревьев Левое скобочное представление Lrep(T): 1. Если a — корень T с поддеревьями T1, T2,
- 34. Пример Семинар 11. Графы: деревья b h i a j k l d e g f
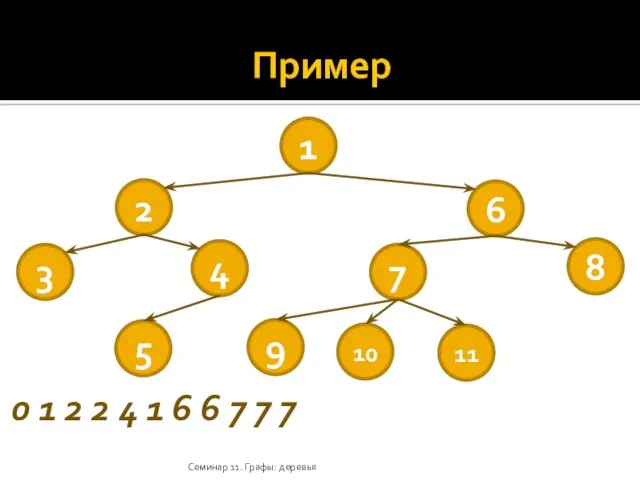
- 35. Представления деревьев Список прямых предков: Составляется список прямых предков для вершин дерева с номерами 1, 2,
- 36. Пример Семинар 11. Графы: деревья 1 2 6 3 4 7 8 5 9 11 10
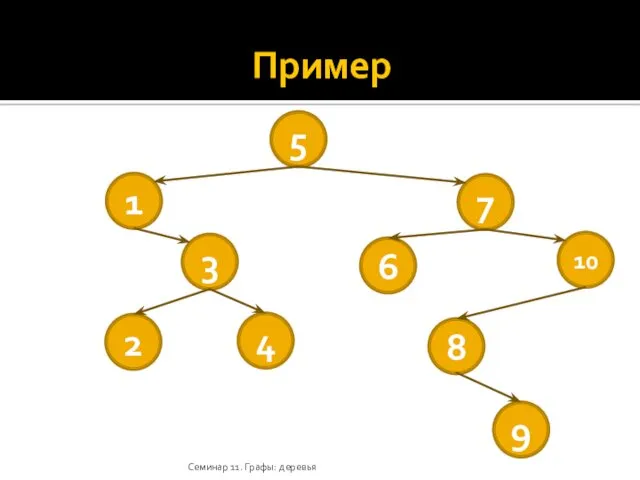
- 37. Дерево двоичного поиска Деревом двоичного поиска для множества S называется помеченное двоичное дерево, каждая вершина v
- 38. Пример Семинар 11. Графы: деревья 5 1 7 3 6 10 2 4 8 9
- 39. Просмотр дерева двоичного поиска Вход: дерево T двоичного поиска для множества S, элемент a. Выход: истина,
- 40. Построение дерева двоичного поиска Вход: последовательность слов произвольной длины. Выход: введённые слова в лексикографическом порядке. Метод:
- 42. Скачать презентацию












![Представление полных бинарных деревьев Массив T[2k - 2]: T[0] —](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/108158/slide-21.jpg)










 Сумма и разность кубов
Сумма и разность кубов Презентация занятия по ФЭМП с использованием ИКТ в подготовительной группена тему: Путешествие в сказку цветик - семицветик
Презентация занятия по ФЭМП с использованием ИКТ в подготовительной группена тему: Путешествие в сказку цветик - семицветик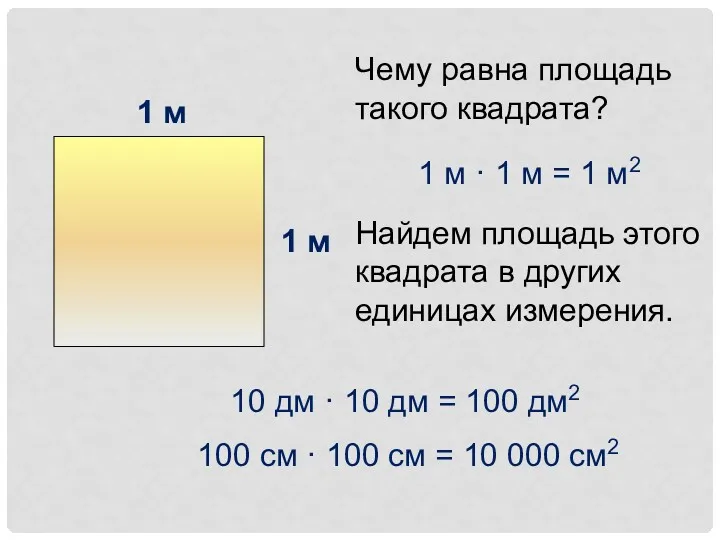 Площадь квадрата
Площадь квадрата Связь между компонентами и результатом умножения
Связь между компонентами и результатом умножения Наглядное представление статистической информации
Наглядное представление статистической информации Эффективные методы, формы и приёмы, используемые при проведении урока математики (начало урока)
Эффективные методы, формы и приёмы, используемые при проведении урока математики (начало урока) Презентация к уроку-путешествию по математике 3 класс Единицы длины
Презентация к уроку-путешествию по математике 3 класс Единицы длины Объемы шарового сегмента, шарового слоя и шарового сектора
Объемы шарового сегмента, шарового слоя и шарового сектора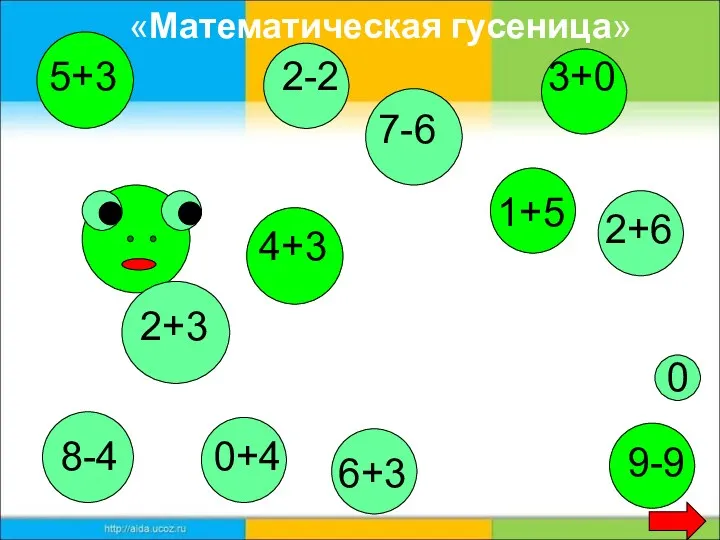 Интерактивный устный счёт Математическая гусеница
Интерактивный устный счёт Математическая гусеница Понятие призмы
Понятие призмы Прямоугольные треугольники и некоторые их свойства
Прямоугольные треугольники и некоторые их свойства Случаи вычитания 16 -
Случаи вычитания 16 - Көпжақтар әлемінде
Көпжақтар әлемінде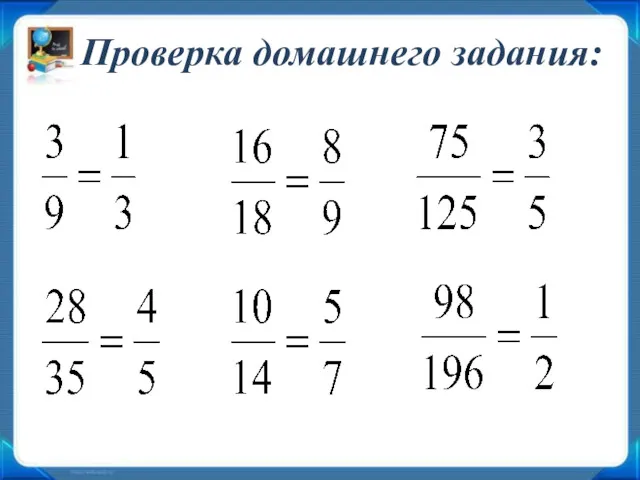 Приведение дробей общему знаменателю
Приведение дробей общему знаменателю математика. Деление.
математика. Деление. Сложение и вычитание дробей с разными знаменателями. 6 класс
Сложение и вычитание дробей с разными знаменателями. 6 класс Повторение испытаний
Повторение испытаний Нахождение числа по его дроби
Нахождение числа по его дроби Вивчаємо арифметичні дії множення і ділення; табличне множення та ділення
Вивчаємо арифметичні дії множення і ділення; табличне множення та ділення Практикум по решению задачи №20 ЕГЭ (базовый уровень)
Практикум по решению задачи №20 ЕГЭ (базовый уровень) Площадь круга и кругового сектора
Площадь круга и кругового сектора Геометриялық пішіндер және денелер
Геометриялық пішіндер және денелер Способы вычисления
Способы вычисления Медианы, биссектрисы, высоты треугольника
Медианы, биссектрисы, высоты треугольника Первый признак равенства треугольников
Первый признак равенства треугольников Повторим решение уравнений
Повторим решение уравнений Дидактическая игра Чего не стало? Диск
Дидактическая игра Чего не стало? Диск Первый признак равенства треугольников. Геометрия. 7 класс
Первый признак равенства треугольников. Геометрия. 7 класс